摘要
本实验旨在设计并仿真控制一阶倒立摆系统,首先通过分析建立该系统的数学模型,并进行理论计算,并使用Matlab进行仿真研究;其次,通过理论方法设计PID控制器,确定控制器结构和参数;最后,通过Matlab仿真控制效果,验算性能指标并分析控制效果。实验过程中使用的数学模型来源于经典的倒立摆控制问题,采用PID控制方法优化系统性能。
一.一阶倒立摆系统的数学模型建立
1.1 一阶倒立摆系统的运动方程式建立

如上图所示,一个可以活动的小车上立着一根不稳定随时会倒下的杆。小车的轮子由电机控制,可以控制小车受到的力的大小和方向。我们可以获取小车的位置和速度,杆相对于垂直位置的倾角和杆的速度。目标就是保持杆不倒下来,同时小车静止在中间的位置。

对小车在水平方向上进行受力分析可得:

对摆在水平方向上进行受力分析可得:
即:
对摆在垂直方向上进行受力分析可得:
即:
关节力矩:
令
由于,则:
化简以上式子可得:
1.2 一阶倒立摆系统的传递函数
对上两式进行拉普拉斯变换得:
令
可得摆的角度的传递函数:
小车的位置的传递函数:
二.未加入PID控制器的系统的特性分析
2.1 稳定性判断
判断系统稳定性问题最简单的方法就是求出该系统的所有极点,并判别是否含有实部大于零的极点(不稳定极点)。如果有这样的极点,则系统称为不稳定系统,否则称为稳定系统。

为了方便我们进行研究,将以上数据代入摆的角度的传递函数可得:
用MATLAB求解摆的角度的传递函数的所有极点的代码和结果如下:
>> den=[1 -0.5477 37.4991 5.3570];
>> roots(den)
ans =
0.3451 + 6.1220i
0.3451 - 6.1220i
-0.1425 + 0.0000i从求得的解可知,该系统不稳定。
2.2 Bode图、响应曲线研究
在Matlab中,我们可以使用以下命令对摆的角度的传递函数的进行仿真研究:
% 定义传递函数
num = [-5.4663 0 0 0]; % 分子系数
den = [1 -0.5477 37.4991 5.3570 0]; % 分母系数
% 创建传递函数模型
P_bai = tf(num, den);
% 绘制系统的 Bode 图
figure;
bode(P_bai);
title('Bode Diagram');
grid on;
% 单位阶跃响应
figure;
step(P_bai);
title('单位阶跃响应');
grid on;
% 单位脉冲响应
figure;
impulse(P_bai);
title('单位脉冲响应');
grid on;获取未加入PID控制器的系统的Bode图、响应曲线如下:



由上图可知,此时传递函数的各方面性能指标不好,难以追踪单位阶跃响应函数与单位脉冲响应函数。
三.PID控制与仿真
3.1 PID控制器的基本原理
PID控制器(Proportional-Integral-Derivative Controller,比例-积分-微分控制器)是工业自动化中常用的一种反馈控制器,广泛应用于温度、压力、速度等系统的控制中。PID控制器通过对系统误差(即目标值与实际输出值之间的差异)的综合处理,来实现对控制对象的精确调节。PID控制器由三部分组成:比例(P)、积分(I)、微分(D),它们分别对误差的不同特征进行响应,具体作用如下:
1. 比例控制(P)
比例控制是最基本的控制方式,它根据当前误差的大小来决定控制量。比例控制的输出与误差成正比,即:
其中:
是比例控制器的输出。
是比例增益。
是当前时刻的误差,即目标值与实际输出值之差。
作用:
- 比例控制对系统误差的响应较快,但通常无法完全消除稳态误差。如果增益过大,系统可能会产生过冲(超调)和振荡;如果增益过小,则系统响应较慢。
2. 积分控制(I)
积分控制通过对过去误差的累积来消除稳态误差。积分部分的作用是对误差进行积分,长期的偏差会导致控制输出的增大,从而消除持久的误差。积分控制的输出可以表示为:
其中:
是积分控制器的输出。
是积分增益。
是误差的累积积分。
作用:
- 积分控制可以消除长期的稳态误差,但过度的积分作用可能导致系统过冲或振荡。
3. 微分控制(D)
微分控制是基于误差变化的速率来预测未来误差,并对系统的响应进行调节。它通过计算误差的导数来预防系统超调。微分控制的输出可以表示为:
其中:
是微分控制器的输出。
是微分增益。
是误差对时间的导数。
作用:
- 微分控制有助于减小系统的过冲和振荡,能够提高系统的稳定性,尤其是在控制过程中误差变化较快时。
4. PID控制器的综合输出
PID控制器的总输出是这三部分的加权和:
其中:
是控制器的输出信号,通常用于调整控制对象的输入。
是当前时刻的误差。
5. PID控制器的调参
PID控制器的性能高度依赖于三个增益参数、
和
的选择。正确的参数调节可以使得控制系统具有良好的稳定性、快速的响应和较小的误差。常见的调节方法包括:
- 手动调节法:通过经验和实验逐步调整三个参数,观察系统的响应。
- Ziegler-Nichols方法:通过实验获得临界增益和临界周期,来自动设定 PID 参数。
- 自动调节法:基于系统响应自动调整 PID 参数。
6. PID控制器的优缺点
-
优点:
- 简单直观,易于理解和实现。
- 适用范围广,能够控制许多类型的动态系统。
- 可以平衡系统的快速响应和稳定性。
-
缺点:
- 参数调节较为复杂,尤其是在非线性或大规模系统中。
- 对噪声敏感,特别是微分项可能会放大噪声,导致系统不稳定。
- 在处理大范围变化或突变时,可能需要进行额外的调整或改进。
3.2 MATLAB 自动调整合适参数的 PID 控制器
使用 MATLAB 自动调整合适参数的 PID 控制器并对经过PID控制器调整后的系统进行仿真研究,代码如下:
% 定义传递函数 P_bai(s) = Phi(s) / U(s)
s = tf('s'); % 创建拉普拉斯变量 s
Phi_s = -5.4663 * s^2; % Phi(s) = -5.4663 * s^2
U_s = s^4 - 0.5477 * s^3 + 37.4991 * s^2 + 5.3570 * s; % U(s) = s^4 - 0.5477 * s^3 + 37.4991 * s^2 + 5.3570 * s
P_bai = Phi_s / U_s; % 定义传递函数 P_bai(s)
% 使用 pidtune 函数自动调整 PID 参数
[Kpid, ~, ~] = pidtune(P_bai, 'PID'); % 设计 PID 控制器
% 显示 PID 控制器的参数
disp('PID 控制器参数:');
disp(Kpid);
% 构建闭环控制系统
closed_loop_system = feedback(Kpid * P_bai, 1);
% 仿真闭环系统的bode图
figure;
bode(closed_loop_system);
title('闭环系统的bode图');
grid on;
% 仿真闭环系统的单位阶跃响应
figure;
step(closed_loop_system);
title('闭环系统的单位阶跃响应');
grid on;
% 仿真闭环系统的单位脉冲响应
figure;
impulse(closed_loop_system);
title('闭环系统的单位脉冲响应');
grid on;代码运行结果如下:


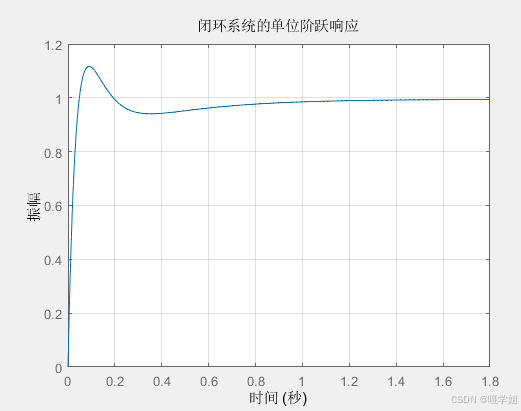

经曲线对比可明显看出,经过PID控制器调整后的系统性能更加优越,能更好的追踪单位阶跃响应函数与单位脉冲响应函数。
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








