目录
前言: 
动态规划的适用条件为最优化原理和无后效性,可以有效地利用历史记录避免重复计算。动态规划一般由三个步骤组成:①定义数组;②求解初始值;③利用状态转移方程求解最优策略。(部分内容参考告别动态规划,连刷40道动规算法题,我总结了动规的套路)
为更好的理解三维DP问题的解法,从一维和二维开始介绍。
一、一维DP
问题1
描述:一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
def g11(n):
if n<=2:
return n
else:
dp=[0 for i in range(n)] #创建n*1的列表
dp[0]=1;dp[1]=2 #初始值
for i in range(2,n):
dp[i]=dp[i-1]+dp[i-2]#递归式:状态转移方程
return dp[n-1]
>>> g11(10)
89二、二维DP
①求方案数
问题2.1
描述:在m*n的方格纸上,一只蚂蚁从左上角(1,1)移动到右下角(m,n),只能往下或者往右移动,每次移动一格,有多少种方案?本题以5*6为例
Ⅰ、数学方法
,其中p=m+n-2,q=m-1
#定义组合函数c(n,m)=n!/m!(n-m)!
#阶层函数:factorial
from math import factorial as f
def c(n,m):
r=int(f(n)/f(m)/f(n-m))
return r
>>> c(9,4)
126Ⅱ、DP
def g21(m,n):
if m==1 or n==1: #显然当列或行为1时,方案唯一
return 1
else:
dp=[[0 for i in range(n)] for j in range(m)] #创建m*n列表用于储存结果
#初始值
for i in range(m): #第一列方案都是1
dp[i][0]=1
for j in range(n): #第一行方案都是1
dp[0][j]=1
#状态转移方程
for i in range(1,m):
for j in range(1,n):
dp[i][j]=dp[i-1][j]+dp[i][j-1]
return dp[m-1][n-1]
>>> g21(5,6)
126②求最小值
问题2.2
描述:在m*n方格纸上,每个格点(行列交叉处)上有未知个数的水滴,蚂蚁从左上角到右下角沾的水滴总数最小是多少? l 为传入的列表,记录了对应点位置的水滴数,例如
l=[[1,2,3]] 对应1*3
l=[[1],[2],[3]] 对应3*1
l=[[1,2],[3,4]] 对应2*2
def g22(l):
[m,n]=[len(l),len(l[0])] #记录l的行列信息
#特殊情况
if m==1:
return sum(l[0])
elif n==1:
return sum([i[0] for i in l])
else:
#创建m*n全0列表
dp=[[0 for i in range(n)] for j in range(m)]
#第一行和第一列作为初始值
for i in range(m):
dp[i][0]=dp[i-1][0]+l[i][0]
for j in range(n):
dp[0][j]=dp[0][j-1]+l[0][j]
#状态转移方程
for i in range(1,m):
for j in range(1,n):
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+l[i][j]
return dp[m-1][n-1]
>>> g22([[1],[2],[3]])
6
>>> g22([[1,2,3]])
6
>>> g22([[1,2,3],[4,5,6]]) #1+2+3+6=12
12三、三维DP
①求方案数
问题3.1
描述:在m*n*p的立方体中,以整数点为格点,蚂蚁每次移动1个单位长度,方向如图所示,从起点到终点共有多少种方案? 本题以3*4*5为例
 Ⅰ、数学方法
Ⅰ、数学方法
,其中,k=m+n+p-3,q=m-1,s=k-q=n+p-2,r=n-1
from math import factorial as f
def c(n,m):
r=int(f(n)/f(m)/f(n-m))
return r
>>> c(9,2)*c(7,3)
1260Ⅱ、DP
def g31(m,n,p):
l=[m,n,p]
#特殊情况降维
if 1 in l:
l.remove(1)
return g21(l[0],l[1])
else:
#创建m*n*p的列表
dp=[[[0 for i in range(p)] for j in range(n)] for k in range(m)]
#初值需计算三个平面,mon,mop,nop,o是原点
#平面内即可降维
for k in range(m):
for j in range(n):
for i in range(p):
l=[k,j,i]
if 0 in [k,j,i]:
l.remove(0)
dp[k][j][i]=g21(l[0]+1,l[1]+1)
#状态转移方程
for k in range(1,m):
for j in range(1,n):
for i in range(1,p):
dp[k][j][i]=dp[k][j][i-1]+dp[k][j-1][i]+dp[k-1][j][i]
return dp[m-1][n-1][p-1]
>>> g31(3,4,5)
1260②求最小值
问题3.2
描述:在m*n*p的立方体中,以整数点为格点,蚂蚁每次移动1个单位长度,方向如图所示,
每个格点都有一定的水滴,问蚂蚁从起点到终点最少沾的水滴数?l为传入的列表,记录了对应位置的水滴数,例如
l=[[[1,2],[3,4]]] 对应 1*2*2
l=[[[1,2]],[[3,4]]] 对应 2*1*2
l=[[[1],[2]],[[3],[4]]]对应 2*2*1
l=[[[1,2],[3,4]],[[1,2],[3,4]]] 对应 2*2*2
def g32(l):
l1=[m,n,p]=[len(l),len(l[0]),len(l[0][0])]
#创立m*n*p全0列表
dp=[[[0 for i in range(p)] for j in range(n)] for k in range(m)]
#特殊情况,降维
if 1 in l1:
a=l1.index(1)
del l1[a]
l2=[[0 for i in range(l1[0])] for j in range(l1[1])]
if a==0:
for j in range(n):
for i in range(p):
print(i,j)
l2[j][i]=l[0][j][i]
elif a==1:
for k in range(m):
for i in range(p):
l2[k][i]=l[k][0][i]
else:
for k in range(m):
for j in range(n):
l2[k][j]=l[k][j][0]
return g22(l2)
else:
#初始值1,三条轴上的赋值
for k in range(m):
dp[k][0][0]=dp[k-1][0][0]+l[k][0][0]
for j in range(n):
dp[0][j][0]=dp[0][j-1][0]+l[0][j][0]
print(dp[0][j][0])
for i in range(p):
dp[0][0][i]=dp[0][0][i-1]+l[0][0][i]
#初始值2,三个平面的赋值
#mon平面
for k in range(1,m):
for j in range(1,n):
dp[k][j][0]=min(dp[k-1][j][0],dp[k][j-1][0])+l[k][j][0]
#nop平面
for j in range(1,n):
for i in range(1,p):
dp[0][j][i]=min(dp[0][j-1][i],dp[0][j][i-1])+l[0][j][i]
#mop平面
for k in range(1,m):
for i in range(1,p):
dp[k][0][i]=min(dp[k-1][0][i],dp[k][0][i-1])+l[k][0][i]
#状态转移方程
for k in range(1,m):
for j in range(1,n):
for i in range(1,p):
dp[k][j][i]=min(dp[k][j][i-1],dp[k][j-1][i],dp[k-1][j][i])+l[k][j][i]
return dp[m-1][n-1][p-1]测试:
>>> g32([[[1,2],[3,4]]] ) #1*2*2
7
>>> g32([[[1,2]],[[3,4]]] ) #2*1*2
7
>>> g32([[[1],[2]],[[3],[4]]]) #2*2*1
7
>>> g32([[[1,2],[3,4]],[[1,2],[3,4]]]) #2*2*2
8四、关于三维DP步骤的解释
以上面传入列表2*2*2 为例说明
 ①先将传入的数据在正方体上标好
①先将传入的数据在正方体上标好
②初始值1,将三条轴上的数据计算出来 
③初始值2,将三个平面上的点对应数据计算出来 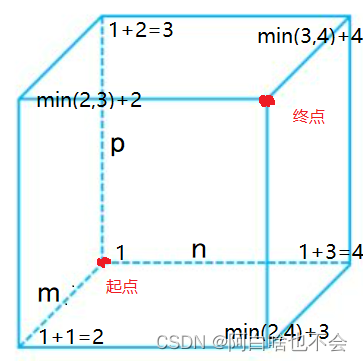
④利用状态转移方程计算 
五、总结
首先,创建相应维度的列表是为了储存到每一点对应题目要求的解,因为要用到递归(状态转移,例如从n--->n-1,n-2),把途经的每一步记录下来减少重复计算,比如说三维DP中dp[k][j][i]对应从原点到该点(k,j,i)的最少水滴数
对于初始值:递归到0,1等时无法用递归式计算,比如-1没有意义,所以需要给定初值
其实,从三维DP的代码就能看出,维数每+1,题目的难度至少上升一个级别,例如,对于四维DP m*p*q*r,给定的初值条件会更多,当维度继续上升时,难度可想而知,这也是DP的一个缺陷,即“维数障碍”

























 1684
1684

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










