支持向量机

最新推荐文章于 2024-07-08 22:12:26 发布

小玉的博客

最新推荐文章于 2024-07-08 22:12:26 发布

阅读量822

点赞数 23

文章标签：支持向量机算法机器学习

本文链接：https://blog.csdn.net/m0_73911859/article/details/139304069

版权

引言

一、SVM的基本原理

1.1 支持向量（Support Vectors）

引言

支持向量机(support vector machines，SVM)是一种二分类模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。SVM模型将实例表示为空间中的点，将使用一条直线分隔数据点。需要注意的是，支持向量机需要对输入数据进行完全标记，仅直接适用于两类任务，应用将多类任务需要减少到几个二元问题。

一、SVM的基本原理

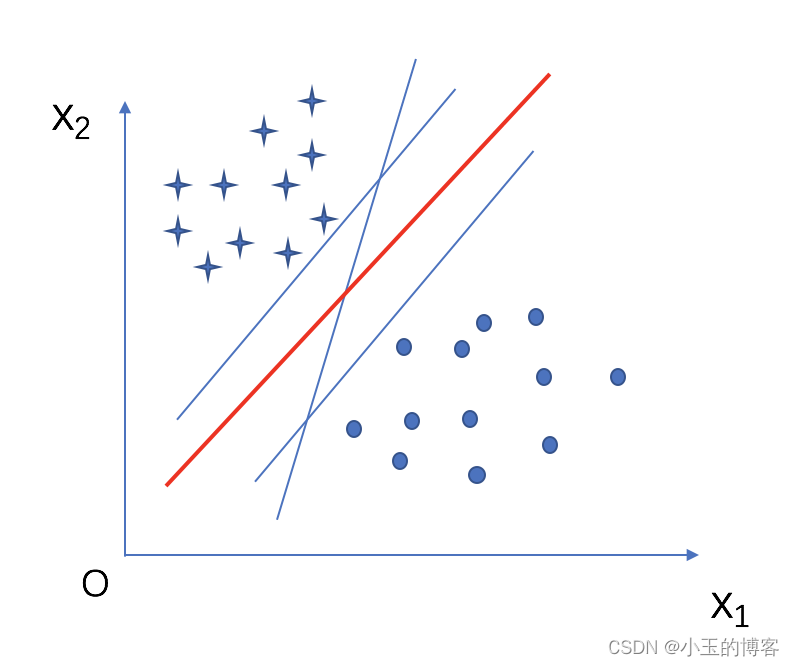
直观上看，应该找位于两类训练样本‘正中间’的划分超平面，即图中的红色平面，因为该划分超平面对训练样本局部扰动的‘容忍’性最好，换言之，这个划分超平面所产生的分类结果是最棒的，泛化能力最强。

在样本空间中，划分超平面可通过如下线性方程来描述：

$w^T x + b = 0$

其中w=(w1;w2;w3...wd)为法向量，决定了超平面的方向，b为位移项，决定了超平面与原点的距离。如果划分超平面可被法向量w和位移b确定，将其记为（w，b),则样本空间中任意点到超平面（w,b)的距离为

$r = \frac{ |w^T x + b|}{\|w\|}$

假设超平面（w,b）能将训练样本正确分类，则对于（Xi , Yi）属于D,若yi = +1，则有 $w^T x + b>0$ ;若yi= -1，则有 $w^T x + b< 0$ ，令

$\begin{cases} w^T x_i + b \geqslant +1 ,yi = +1\\ w^T x_i + b \leqslant -1 ,yi = -1 \end{cases}$

如图所示，距离超平面最近的这几个训练样本点使以上等式的等号成立，她们被称为支持向量。

1.1 支持向量（Support Vectors）

支持向量是图2中距离超平面最近的几个样本点，它们恰好位于两个平行的虚线（间隔边界）上。这些支持向量是唯一需要的样本点，因为它们包含了定义最优超平面的所有必要信息。

1.2 间隔（margin）

两个异类支持向量到超平面的距离之和 r 被称为间隔

$r = \frac{ 2}{\|w\|}$

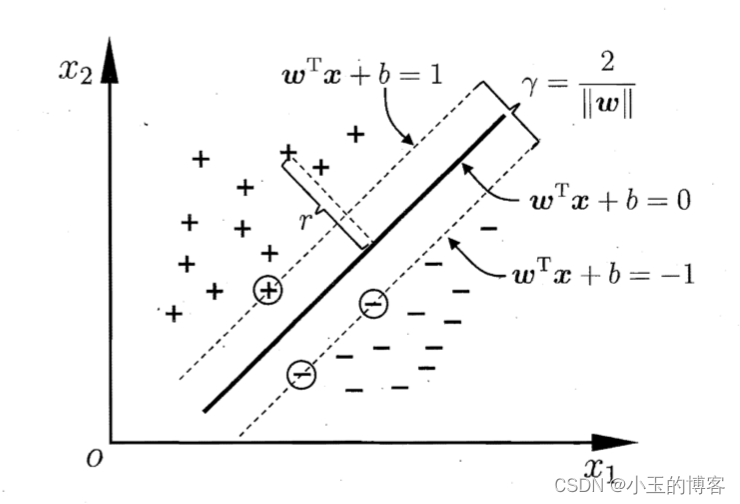
支持向量机（SVM）的核心就是解决优化问题，以找到最佳的超平面来分隔不同类别的数据，这个优化问题可以分为两种：硬间隔优化和软间隔优化

1.3 硬间隔与软间隔

硬间隔SVM:

找到一个超平面，它能够完美地将不同类别的数据点分开，同时最大化两类数据点之间的间隔。在硬间隔分类中，模型不允许任何分类错误，即所有的训练数据点都必须被正确分类到它们对应的类别中。

局限性：如果数据集中存在噪声或异常点，硬间隔SVM可能会过拟合这些点，因为它试图完美地拟合所有数据。

软间隔SVM：

对于线性不可分的数据集，硬间隔SVM可能无法找到解。软间隔SVM通过引入松弛变量（slack variables）来允许一定程度的分类错误，从而提高了模型的泛化能力。软间隔SVM的目标是在最大化间隔的同时，最小化分类错误的数量。

$\min_{w,b,\xi} \left[ \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{N} \xi_i \right]$

$subject \ to\ y_i(w \cdot x_i + b) \geq 1 - \xi_i$

其中 $\xi _i\geq 0$ ，w 是权重向量，b 是偏置项，xi 是输入特征，yi 是标签（+1 或 −1），C 是一个正的调节参数，它控制着模型在误差项和正则化项之间的权衡。

C值较大：模型更倾向于硬间隔分类，对分类错误的容忍度较低，可能导致过拟合。

C值较小：模型对分类错误的容忍度较高，可以更好地泛化到新数据，但可能在训练集上的分类效果较差。

通过不同C值的大小可以看到不同的分类效果：

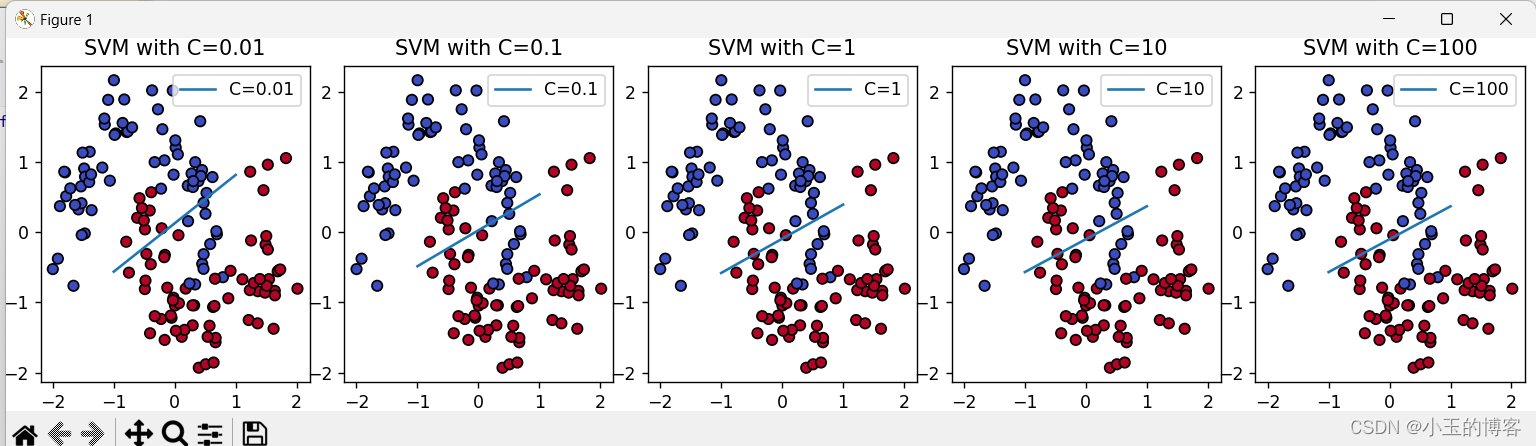
1.4 正则化的重要性

由图3中可以知道，正则化的主要目的是防止模型过拟合。过拟合发生在模型对训练数据的细节和噪声学习得过多，导致模型在新的、未见过的数据上表现不佳。通过正则化，可以限制模型的复杂度，使其在训练数据上的表现和新数据上的泛化能力之间取得平衡。

1.5对偶问题

1.5.1拉格朗日乘子法

支持向量机（SVM）的对偶问题是在求解SVM原始问题时引入拉格朗日乘子法后得到的优化问题。SVM的原始问题是寻找一个决策边界，使得数据点正确分类的同时最大化间隔。原始问题通常是一个凸二次规划问题，涉及不等式约束。

为了求解这个问题，我们引入拉格朗日乘子 αi 并构建拉格朗日函数：

$L(w, b, \alpha) = \frac{1}{2} \|w\|^2 +\sum_{i=1}^N \alpha_i [y_i(w^T x_i + b) - 1]$

其中，𝛼𝑖≥0。

对偶问题是通过将原始问题的拉格朗日函数对 w 和 b 进行最小化，然后对得到的函数进行最大化得到的。对 w 和 b 的最小化可以简化为：

$w = \sum_{i=1}^{N} \alpha_i y_i x_i$

将 w 代入 L 并最小化 b 通常会导致 b 被消去，因此对偶问题只涉及 α。对偶问题的最终形式是：

$\max_{\alpha} \left[ -\frac{1}{2} \sum_{i,j=1}^N \alpha_i \alpha_j y_i y_j (x_i^T x_j) + \sum_{i=1}^N \alpha_i \right]$ $\quad \text{subject to} \quad\sum_{i=1}^N \alpha_i y_i = 0, \quad \alpha_i \geq 0$

解出α后，求出w和b即可得到模型：

二、线性可分与非线性问题

2.1 线性可分数据的SVM

支持向量机（SVM）模型在处理线性可分问题时，目标是找到一个最优的超平面，使得不同类别的样本尽可能的分开。这个最优的超平面被称为最大边距超平面，它是根据学习样本求解出的最大边距确定的。具体来说，线性可分的支持向量机要求训练集线性可分，通过硬间隔最大化得到超平面。

2.2 非线性数据的SVM

对于线性不可分的情况，支持向量机（SVM）需要采取不同的策略。由于数据中有些样本点距离太近，不能满足函数间隔大于等于的约束条件，因此线性可分的支持向量机学习方法在这种情况下是不适用的。
此时，我们可以使用核技巧最优化来求解。具体来说，我们可以通过使用核函数将线性不可分的训练集映射到高维空间中，使其变为线性可分的数据集。然后，在新的高维特征空间中寻找最优分隔超平面。

三、线性可分数据SVM的实现（代码）

LinearSVM类：定义了一个名为LinearSVM的类，它包含了初始化方法、拟合（fit）方法和预测（predict）方法。初始化方法设置了学习速率、正则化参数λ以及迭代次数。拟合方法通过梯度下降法优化权重向量w和偏置项b，以最大化间隔并最小化经验误差。预测方法基于优化后的模型参数对给定数据点进行分类。

class LinearSVM:
    def __init__(self, learning_rate=0.0001, lambda_param=0.1, n_iters=1000):
        # 初始化学习率（learning_rate）、正则化参数（lambda_param）和迭代次数（n_iters）
        self.learning_rate = learning_rate
        self.lambda_param = lambda_param
        self.n_iters = n_iters
        # 初始化权重向量和偏置项为None
        self.w = None
        self.b = None

模型训练：fit 方法接受特征矩阵 X 和标签向量 y 作为输入。首先，将标签转换为-1或1，然后初始化权重向量 w 为零向量，偏置项 b 为0。通过迭代每个数据点，根据间隔条件更新权重和偏置，实现模型的训练。

   def fit(self, X, y):
        # 获取数据点的数量和特征数量
        n_samples, n_features = X.shape

        # 将标签二值化，0转换为-1，其他保持不变
        y_ = np.where(y <= 0, -1, 1)

        # 初始化权重向量为零向量，偏置项为0
        self.w = np.zeros(n_features)
        self.b = 0

        # 迭代n_iters次
        for _ in range(self.n_iters):
            # 对每一个数据点进行更新
            for idx, x_i in enumerate(X):
                # 计算当前数据点的间隔条件
                condition = y_[idx] * (np.dot(x_i, self.w) - self.b) >= 1
                if condition:
                    # 如果数据点正确分类且在间隔外，仅通过正则项更新权重
                    self.w -= self.learning_rate * (2 * self.lambda_param * self.w)
                else:
                    # 如果数据点错误分类或在间隔内，权重更新包括误差项和正则项
                    self.w -= self.learning_rate * (2 * self.lambda_param * self.w - np.dot(x_i, y_[idx]))
                    self.b -= self.learning_rate * y_[idx]

预测：predict 方法根据训练得到的权重向量 w 和偏置项 b，对输入的特征矩阵 X 进行预测，返回每个样本的预测标签。

 def predict(self, X):
        # 计算线性输出并返回符号，即预测结果
        linear_output = np.dot(X, self.w) - self.b
        return np.sign(linear_output)

数据准备：使用datasets.make_blobs函数生成了包含两个类别、100个样本的二维数据集，并将标签转换为-1和1以便于后续的SVM处理。

# 数据准备和模型训练
# 生成100个样本，2个中心的高斯分布数据
X, y = datasets.make_blobs(n_samples=100, centers=2, random_state=6)

模型训练与评估：创建了LinearSVM类的实例，并使用生成的数据对其进行训练。训练完成后，打印出学习到的权重向量w和偏置项b。

# 将标签调整为-1和1
y = np.where(y == 0, -1, 1)
# 创建LinearSVM实例并训练模型
svm = LinearSVM()
svm.fit(X, y)

# 训练完成后输出w和b的值
print("权重向量 w:", svm.w)
print("偏置项 b:", svm.b)

效果图：

可视化结果：定义了一个plot_hyperplane函数来可视化训练结果。该函数绘制了数据点及其分类，并展示了由训练得到的超平面作为决策边界，清晰地划分了两类数据。最后调用此函数展示分类效果。

# 可视化结果
def plot_hyperplane(X, y, w, b):
    # 绘制数据点，使用viridis颜色映射
    plt.scatter(X[:, 0], X[:, 1], marker='o', c=y, s=100, edgecolors='k', cmap='viridis')

    # 绘制决策边界
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()

    # 创建用于绘制决策边界的网格数据
    xx = np.linspace(xlim[0], xlim[1], 30)
    yy = np.linspace(ylim[0], ylim[1], 30)
    YY, XX = np.meshgrid(yy, xx)
    xy = np.vstack([XX.ravel(), YY.ravel()]).T

    # 计算决策边界的值
    Z = (np.dot(xy, w) - b).reshape(XX.shape)
    # 绘制决策边界
    ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])

    # 显示图像
    plt.show()

# 使用训练好的模型绘制超平面
plot_hyperplane(X, y, svm.w, svm.b)

效果图：

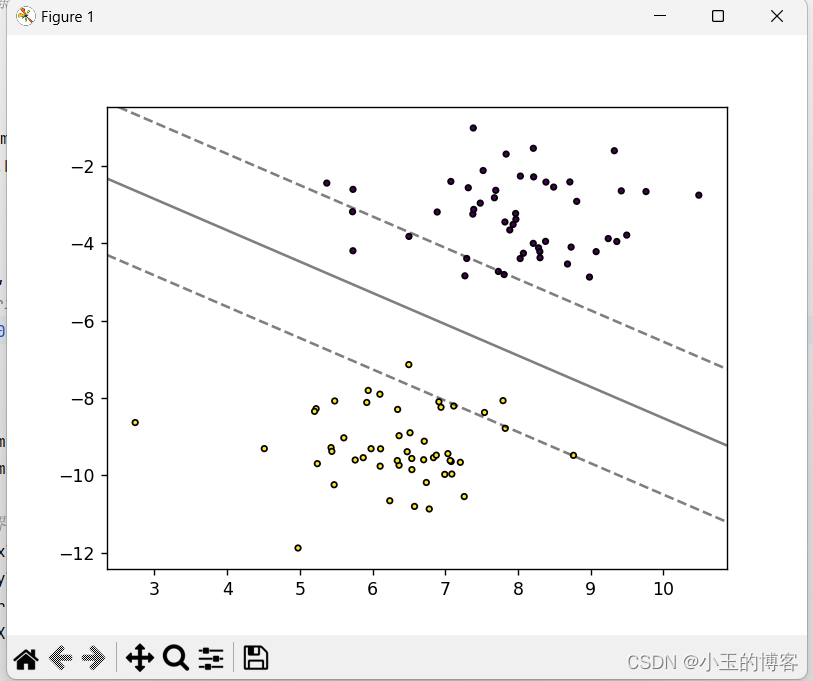
完整代码

import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt

# 定义线性支持向量机（SVM）类
class LinearSVM:
    def __init__(self, learning_rate=0.0001, lambda_param=0.1, n_iters=1000):
        # 初始化学习率，正则化参数，迭代次数
        self.learning_rate = learning_rate
        self.lambda_param = lambda_param
        self.n_iters = n_iters
        # 初始化权重向量和偏置项为None
        self.w = None
        self.b = None

    def fit(self, X, y):
        # 获取数据点的数量和特征数量
        n_samples, n_features = X.shape

        # 将标签二值化，0转换为-1，其他保持不变
        y_ = np.where(y <= 0, -1, 1)

        # 初始化权重向量为零向量，偏置项为0
        self.w = np.zeros(n_features)
        self.b = 0

        # 迭代n_iters次
        for _ in range(self.n_iters):
            # 对每一个数据点进行更新
            for idx, x_i in enumerate(X):
                # 计算当前数据点的间隔条件
                condition = y_[idx] * (np.dot(x_i, self.w) - self.b) >= 1
                if condition:
                    # 如果数据点正确分类且在间隔外，仅通过正则项更新权重
                    self.w -= self.learning_rate * (2 * self.lambda_param * self.w)
                else:
                    # 如果数据点错误分类或在间隔内，权重更新包括误差项和正则项
                    self.w -= self.learning_rate * (2 * self.lambda_param * self.w - np.dot(x_i, y_[idx]))
                    self.b -= self.learning_rate * y_[idx]

    def predict(self, X):
        # 计算线性输出并返回符号，即预测结果
        linear_output = np.dot(X, self.w) - self.b
        return np.sign(linear_output)

# 数据准备和模型训练
# 生成100个样本，2个中心的高斯分布数据
X, y = datasets.make_blobs(n_samples=100, centers=2, random_state=6)
# 将标签调整为-1和1
y = np.where(y == 0, -1, 1)
# 创建LinearSVM实例并训练模型
svm = LinearSVM()
svm.fit(X, y)

# 训练完成后输出w和b的值
print("权重向量 w:", svm.w)
print("偏置项 b:", svm.b)


# 可视化结果
def plot_hyperplane(X, y, w, b):
    # 绘制数据点，使用viridis颜色映射
    plt.scatter(X[:, 0], X[:, 1], marker='o', c=y, s=100, edgecolors='k', cmap='viridis')

    # 绘制决策边界
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()

    # 创建用于绘制决策边界的网格数据
    xx = np.linspace(xlim[0], xlim[1], 30)
    yy = np.linspace(ylim[0], ylim[1], 30)
    YY, XX = np.meshgrid(yy, xx)
    xy = np.vstack([XX.ravel(), YY.ravel()]).T

    # 计算决策边界的值
    Z = (np.dot(xy, w) - b).reshape(XX.shape)
    # 绘制决策边界
    ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])

    # 显示图像
    plt.show()

# 使用训练好的模型绘制超平面
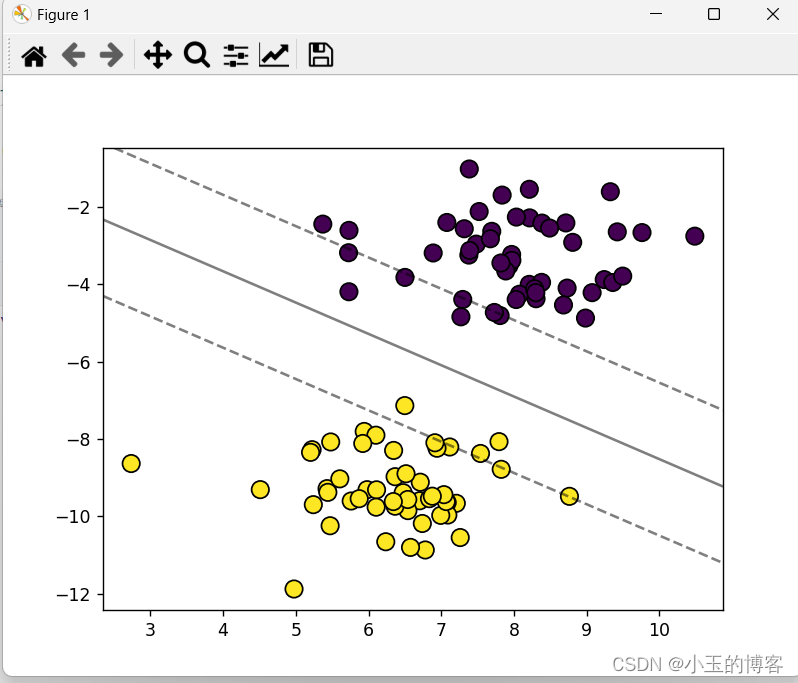
plot_hyperplane(X, y, svm.w, svm.b)

代码运行结果：

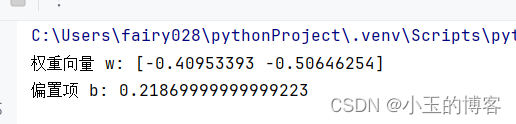
通过自定义的LinearSVM类实现了一个线性支持向量机模型，并利用Scikit-learn的make_blobs函数生成的两分类数据集进行了训练。在完成训练后，模型的权重向量w和偏置项b被输出。随后，通过plot_hyperplane函数，代码绘制了数据点的散点图，其中不同颜色代表不同类别，并展示了由该线性SVM模型定义的决策边界，即超平面。决策边界成功地将两类数据分开，视觉化呈现了模型对新数据点进行分类的规则。

输出w和b的值

五、SVM的优缺点

优点：

高维数据的处理能力：SVM通过核技巧有效地处理高维数据。
泛化能力强：通过优化间隔，SVM具有良好的泛化能力。
对于非线性问题的有效性：通过核函数，SVM能够处理非线性可分问题。

缺点：

对核函数和参数选择敏感：核函数和参数的选择对模型性能有显著影响。
大规模数据集效率问题：在处理大规模数据集时，SVM的训练过程可能比较慢。
对异常值敏感：SVM对异常值和噪声数据比较敏感。

结语

在本次实践中，我们通过编写自定义的线性支持向量机（Linear SVM）算法，深入理解了SVM的工作原理和实现过程。从初始化参数到模型训练，再到参数调优和结果可视化，我们见证了一个强大的分类器是如何从基础数学原理演化而来的。通过逐步构建LinearSVM类，我们不仅实现了SVM的核心功能，还学习了如何通过迭代优化算法来更新模型参数，以及如何通过正则化技术来防止模型过拟合。此外，我们还掌握了如何将模型的预测结果可视化，这对于理解模型决策过程和评估模型性能至关重要。尽管我们的实现是一个基础版本，但它展示了SVM在处理线性可分数据时的有效性。在现实世界的应用中，SVM算法可以扩展到更复杂的核技巧，以处理非线性问题，这进一步增强了其在各种领域的应用潜力。最终，我们通过调整学习率、正则化参数和迭代次数等关键超参数，展示了如何对模型进行微调以获得更好的性能。这强调了参数选择对于机器学习模型成功的重要性。随着技术的不断进步，我们期待在未来看到更多创新的SVM变体和应用，以解决更广泛的数据科学问题。

参考文献：

原文链接：https://blog.csdn.net/qq_48361010/article/details/134960283

小玉的博客

关注

23
点赞
踩
8

收藏

觉得还不错? 一键收藏
0
评论
支持向量机

在本次实践中，我们通过编写自定义的线性支持向量机（Linear SVM）算法，深入理解了SVM的工作原理和实现过程。从初始化参数到模型训练，再到参数调优和结果可视化，我们见证了一个强大的分类器是如何从基础数学原理演化而来的。通过逐步构建LinearSVM类，我们不仅实现了SVM的核心功能，还学习了如何通过迭代优化算法来更新模型参数，以及如何通过正则化技术来防止模型过拟合。此外，我们还掌握了如何将模型的预测结果可视化，这对于理解模型决策过程和评估模型性能至关重要。
复制链接

扫一扫