【2022.12.9每天四个简单题之简单题大智慧系列3】（数组的右下半部分，数组的左下半部分，数组的下方区域，数组的右方区域 ）

ok，今天接着昨天的找规律的题目，继续开始我们的找规律之旅吧！

数组的右下半部分

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的右下半部分元素的平均值或元素的和。

右下半部分是指次对角线下方的部分，如下图所示，黄色部分为对角线，绿色部分为右下半部分：

输入格式
第一行输入一个大写字母，若为 S，则表示需要求出右下半部分的元素的和，若为 M，则表示需要求出右下半部分的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
S
9.7 -4.9 6.1 -6.1 -9.6 1.0 -3.2 0.6 3.2 -9.8 4.9 1.2
-2.8 -5.3 2.8 -1.9 -5.4 7.5 -2.0 5.7 2.3 5.3 -7.5 8.9
6.0 4.3 3.8 -6.7 8.1 -0.5 7.8 -2.2 -1.0 4.0 -4.9 -9.4
5.4 3.7 -6.5 -3.9 -3.3 4.1 -2.5 -4.7 8.2 1.4 1.8 4.7
2.4 9.0 -4.3 9.6 8.6 -6.1 -7.4 8.6 5.6 0.5 -0.4 5.2
-5.2 2.9 -5.6 4.0 -0.2 3.8 -4.1 -1.6 -3.8 -3.1 -1.1 3.3
-9.4 -1.4 0.6 6.5 -4.3 -8.3 6.1 2.9 -5.2 2.5 9.8 -7.7
-2.9 -3.6 7.9 -5.8 -4.7 8.2 -6.2 1.0 7.4 -1.0 -4.4 -4.5
0.1 9.5 4.9 1.5 0.8 -8.2 0.4 9.5 -0.8 -0.9 9.7 -2.1
0.1 -7.6 7.8 -6.9 5.5 1.4 4.0 7.8 1.0 -1.2 9.7 -1.9
-4.6 2.3 -5.5 8.2 -4.8 -3.7 5.4 0.2 -2.4 -0.8 7.4 0.0
-0.1 8.2 0.8 -3.5 -7.6 -0.5 5.6 8.4 -8.6 0.9 9.0 -7.5
输出样例：
53.0
嘿！看到这个题，我们想到了昨天做的那个求左上方的题目，它的规律是i（竖行）+j（横行）<11
那我们可以由互补的思想得出，这里的规律是i+j>11
当然如果您没看过那篇文章，在这里也会给您重新解释一遍
首先我们设竖行是i，横行为j，那么我们可以观察出第一行是没有绿色格子的，而第二行只有一个绿色格子，在最后面，同理我们也可以看到第三行，第四行。。。。。。通过这些也可以发现，对于每一个绿色方格，都满足i+j>11，当然，您也可以通过for循环一遍一遍然后让j先从最大值后然后递减也可以做到。
代码：

#include<cstdio>
using namespace std;
int main()
{
    char a;
    scanf("%c",&a);
    double m,sum=0 ,cnt=0;
    for(int i=0;i<12;i++){
        for(int j=0;j<12;j++){
            scanf("%lf ",&m);
            if(i+j>11){
                sum+=m;
                cnt++;
            }
        }
    }
    printf("%.1f",a=='S'?sum:sum/cnt);
    return 0;
}

数组的左下半部分

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的左下半部分元素的平均值或元素的和。

左下半部分是指主对角线下方的部分，如下图所示，黄色部分为对角线，绿色部分为左下半部分：

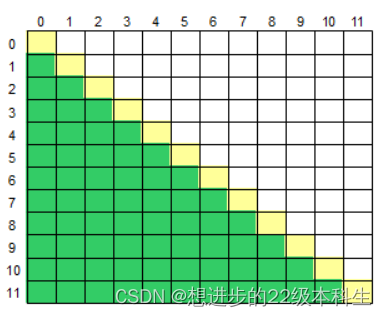
输入格式
第一行输入一个大写字母，若为 S，则表示需要求出左下半部分的元素的和，若为 M，则表示需要求出左下半部分的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
S
8.7 5.6 -2.0 -2.1 -7.9 -9.0 -6.4 1.7 2.9 -2.3 8.4 4.0
-7.3 -2.1 0.6 -9.8 9.6 5.6 -1.3 -3.8 -9.3 -8.0 -2.0 2.9
-4.9 -0.5 -5.5 -0.2 -4.4 -6.1 7.6 6.9 -8.0 6.8 9.1 -8.5
-1.3 5.5 4.6 6.6 8.1 7.9 -9.3 9.6 4.6 0.9 -3.5 -4.3
-7.0 -1.2 7.0 7.1 -5.7 7.8 -2.3 4.3 0.2 -0.4 -6.6 7.6
-3.2 -5.4 -4.7 4.7 3.6 8.8 5.1 -3.1 -2.9 2.8 -4.3 -1.4
-1.8 -3.3 -5.6 1.8 8.3 -0.5 2.0 -3.9 -1.0 -8.6 8.0 -3.3
-2.5 -9.8 9.2 -0.8 -9.4 -0.5 1.6 1.5 3.4 -0.1 7.0 -6.2
-1.0 4.9 2.2 -8.7 -0.9 4.8 2.3 2.0 -3.2 -7.5 -4.0 9.9
-1.1 -2.9 8.7 3.6 7.4 7.8 10.0 -9.0 1.6 8.3 6.3 -5.8
-9.9 0.6 2.0 -3.8 -6.3 0.6 7.3 3.8 -7.1 9.5 2.2 1.3
-2.8 -9.1 7.1 -0.2 0.6 -6.5 1.1 -0.1 -3.6 4.0 -5.4 1.1
输出样例：
-2.8
同样的，由昨天的那个右上方的题目，当时他的规律是j>i
那我们也可以看到这个图，以最后一行为例，是第十一行也就是i=11时，蓝色方格一共10个分别是从第一列直到第十列，故而此行中绿色方格中i与j的性质关系是：i>j；再看剩下的几行，也都满足此性质，也可得出此规律
代码：

#include<cstdio>
using namespace std;
int main()
{
    char a;
    scanf("%c",&a);
    double m,sum=0,cnt=0;
    for(int i=0;i<12;i++){
        for(int j=0;j<12;j++){
            scanf("%lf ",&m);
            if(j<i){
                sum+=m;
                cnt++;
            }
        }
    }
    printf("%.1f",a=='S'?sum:sum/cnt);
    return 0;
}

数组的下方区域

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的下方区域元素的平均值或元素的和。

数组的两条对角线将数组分为了上下左右四个部分，如下图所示，黄色部分为对角线，绿色部分为下方区域：

输入格式
第一行输入一个大写字母，若为 S，则表示需要求出下方区域的元素的和，若为 M，则表示需要求出下方区域的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
S
-6.0 0.7 -8.4 -5.7 -4.1 7.6 9.5 -9.7 4.1 0.6 -6.5 -4.9
6.6 4.9 -3.1 5.3 0.3 -4.5 3.9 -1.5 6.6 7.0 5.1 2.5
-8.5 1.8 -2.7 0.1 -4.9 -7.2 4.3 6.0 -1.4 2.7 -3.0 2.0
4.8 -7.0 -1.3 0.8 1.0 4.5 -1.1 -2.9 -3.9 -3.9 -8.9 5.8
-2.1 -9.6 5.1 0.2 1.0 -1.7 6.4 4.1 2.8 -6.9 2.4 9.3
-6.0 -9.1 -7.0 -7.0 7.8 5.1 6.9 -7.6 0.4 -7.2 5.5 6.0
-1.9 5.5 1.9 -8.5 -5.3 2.3 -9.3 2.0 -0.2 1.2 5.6 -1.8
8.2 2.3 3.5 1.4 4.0 -5.1 -6.9 -2.8 1.7 -7.0 7.8 1.8
-6.0 -4.1 -4.6 -9.4 -4.9 -4.1 4.2 6.3 -2.8 8.7 8.1 -0.9
8.8 -6.5 -4.3 6.1 -6.2 -3.9 -7.0 7.3 5.0 -0.9 -0.0 5.6
-2.4 1.4 8.5 -2.2 0.9 5.3 3.6 8.8 -8.1 3.0 -3.1 6.5
-3.8 -6.4 2.3 4.2 -9.8 -0.3 -9.9 -7.4 3.5 1.5 -0.2 7.0
输出样例：
-11.9
首先我们有今天的第一题可以发现，此题的绿色方格就是第一题的绿色方格再扣除了右上方部分所以它应该具有第一题的性质，也就是i+j>11
其次，它也可以看成是第一题与第二题绿色方格的交汇部分，也就是说它就类似于第一题和第二题的交集，故也满足第二题的性质：i>j
故而代码为：

#include<cstdio>
using namespace std;
int main()
{
    char a;
    scanf("%c",&a);
    double m,sum=0,cnt=0;
    for(int i=0;i<12;i++){
        for(int j=0;j<12;j++){
            scanf("%lf ",&m);
            if(i>j&&i+j>11){
                sum+=m;
                cnt++;
            }
        }
    }
    printf("%.1f",a=='S'?sum:sum/cnt);
    return 0;
}

数组的右方区域

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的右方区域元素的平均值或元素的和。

数组的两条对角线将数组分为了上下左右四个部分，如下图所示，黄色部分为对角线，绿色部分为右方区域：

输入格式
第一行输入一个大写字母，若为 S，则表示需要求出右方区域的元素的和，若为 M，则表示需要求出右方区域的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
S
2.4 7.8 9.4 -5.6 6.9 -4.9 4.8 0.8 3.6 1.7 -1.4 9.7
-6.8 -3.7 -2.0 -4.9 -4.5 -5.3 6.1 7.5 -4.3 5.9 -9.5 9.7
-6.5 -0.4 1.6 3.7 -4.4 -3.3 1.9 7.7 -1.4 4.5 7.4 -3.0
-1.2 0.4 9.8 9.8 -4.3 -1.3 -1.6 0.5 2.8 -4.0 8.5 3.9
0.2 -2.0 -6.4 -9.8 3.7 -2.0 1.7 -3.6 -3.4 2.4 -1.2 -3.9
-8.3 5.8 -1.0 -4.4 1.0 -2.4 2.8 -4.6 2.1 8.7 -6.8 -8.3
6.3 -6.8 -7.0 9.3 -7.7 -1.7 8.2 -6.5 -1.8 6.7 8.2 4.4
0.4 8.6 -1.2 8.6 -4.6 1.8 9.6 1.6 2.0 -1.0 3.9 -9.2
7.5 -3.1 6.2 -4.5 -3.0 2.5 -7.7 2.9 0.3 3.3 -2.7 3.4
-5.0 3.0 -0.0 4.3 9.5 -0.0 -9.9 -8.6 -0.9 -5.5 7.7 6.5
4.9 -9.6 -2.9 8.5 2.0 -9.9 -4.9 -1.5 -2.4 -7.6 1.7 8.5
-6.4 6.8 -3.7 -4.7 0.2 5.8 -5.4 0.6 7.0 -4.2 -7.5 -2.4
输出样例：
40.9
同理，此题就是右上方部分和右下方部分的交集
由昨天的右上方部分的规律可知，他满足规律：i<j
然后又由今天的第一题可知它还满足规律：i+j>11
故而代码如下：

#include<cstdio>
using namespace std;
int main()
{
    char a;
    scanf("%c",&a);
    double m,sum=0,cnt=0;
    for(int i=0;i<12;i++){
        for(int j=0;j<12;j++){
            scanf("%lf ",&m);
            if(j>i&&i+j>11){
                sum+=m;
                cnt++;
            }
        }
    }
    printf("%.1f",a=='S'?sum:sum/cnt);
    return 0;
}

希望这几个找规律的题可以给大家一点帮助！