打破数据分析壁垒：SPSS复习必备（七）

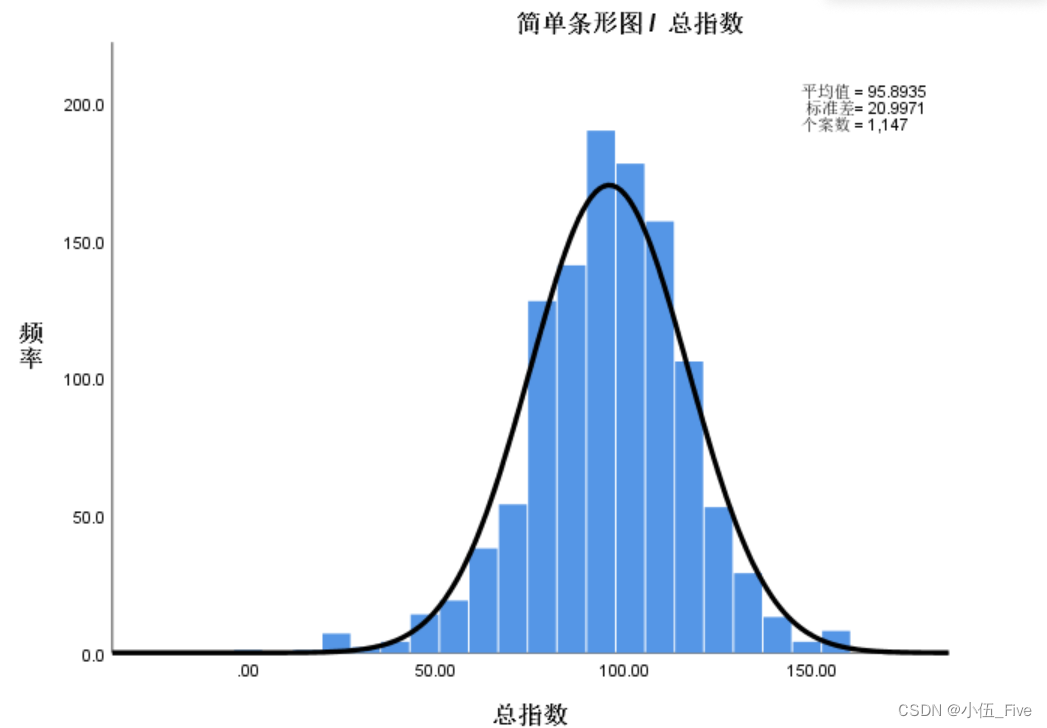
一、直方图与茎叶图

直方图 ，用于表示 连续性变量的频数分布，在实际应用中常用于考察变量的分布是否服从某种分布类型，如正态分布。在直方图中以各矩形（直条）的面积表示各组段的频数(或频率)，各矩形的面积总和为总频数（或等于1）。若各组段组距不等，则以各组段组距除该组段频数之商为矩形的高度，以该组段的组距为矩形的宽度，以保证矩形的面积等于该组的频数。

看个栗子

1)选择 "图形” →“图表构建器 "菜单项，打开"图表构建器"对话框

直方图组的绘制

选择"组 /点ID",选择行面积变量，放入对比元素即可

分段直方图

面积图

茎叶图

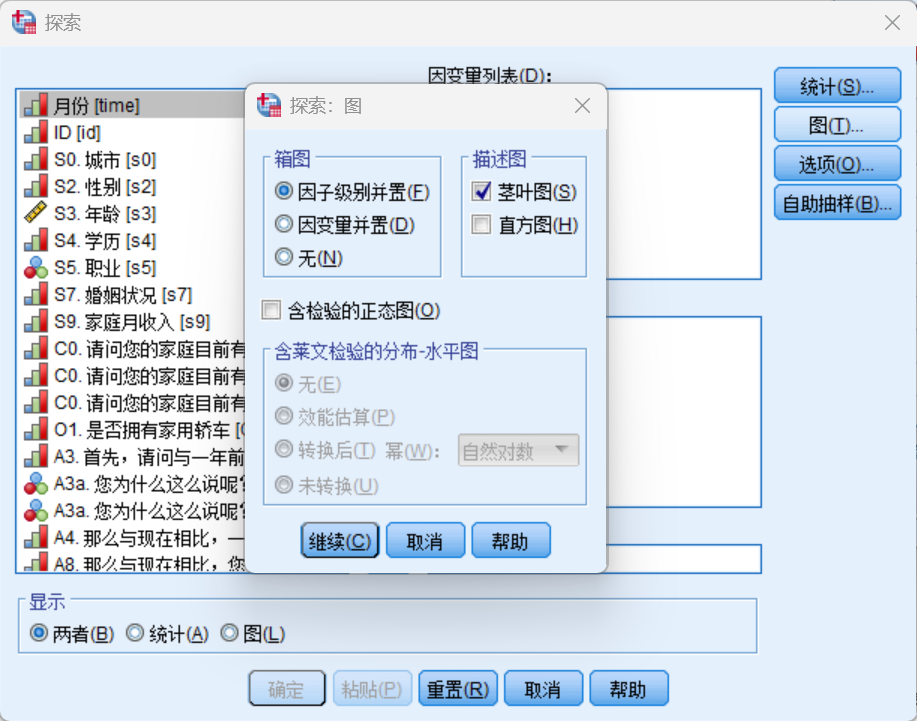
分析->  描述统计->  探索过程实现

二、箱图

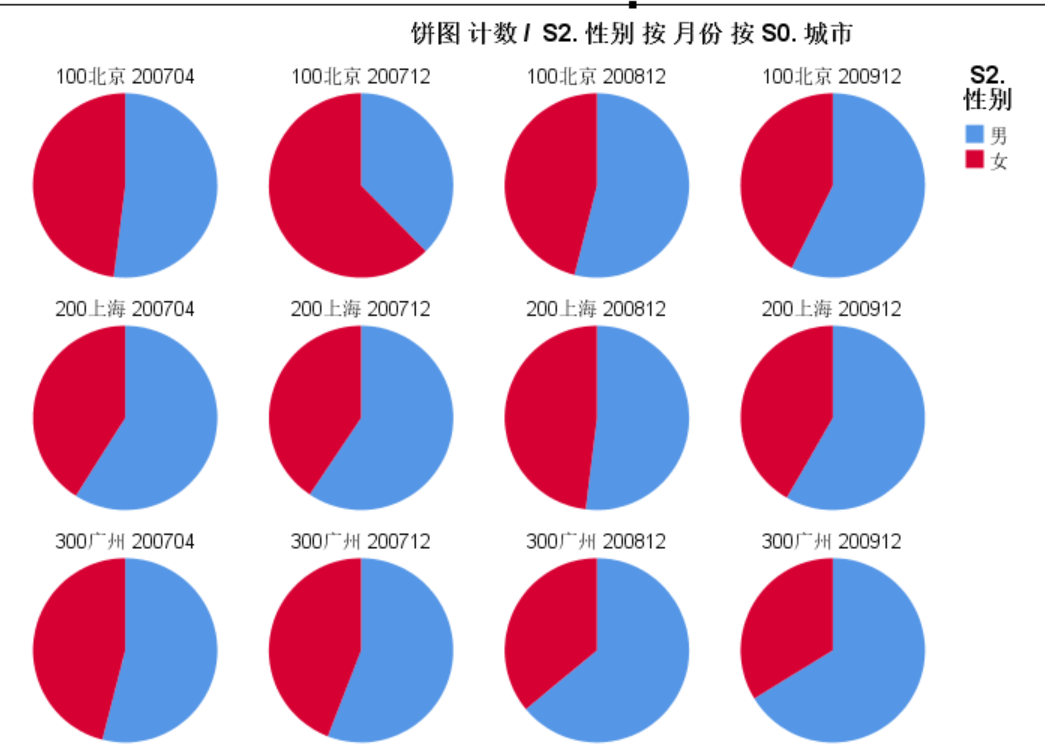
三、饼图

条形图设置降序

在"排序依据“下拉列表框 选择"统计”  选项，在 “ 方向”  拉列 表框 选择"降序"选项 ，单 击"应用'按钮

四、百分条图

五、多重线图

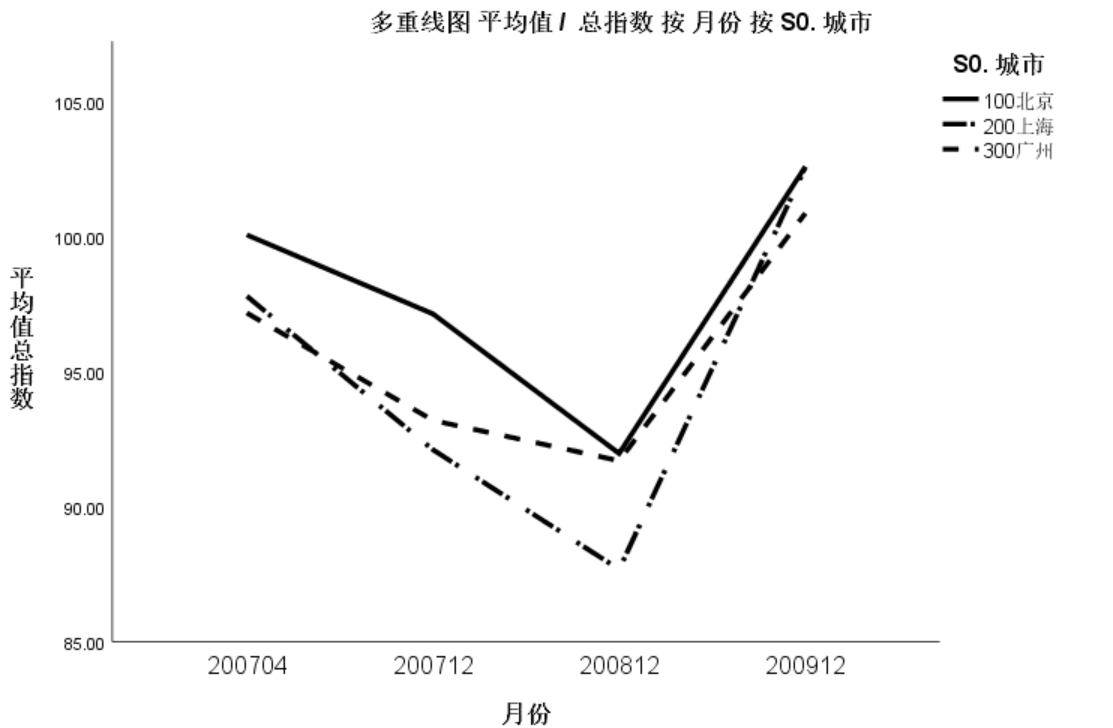
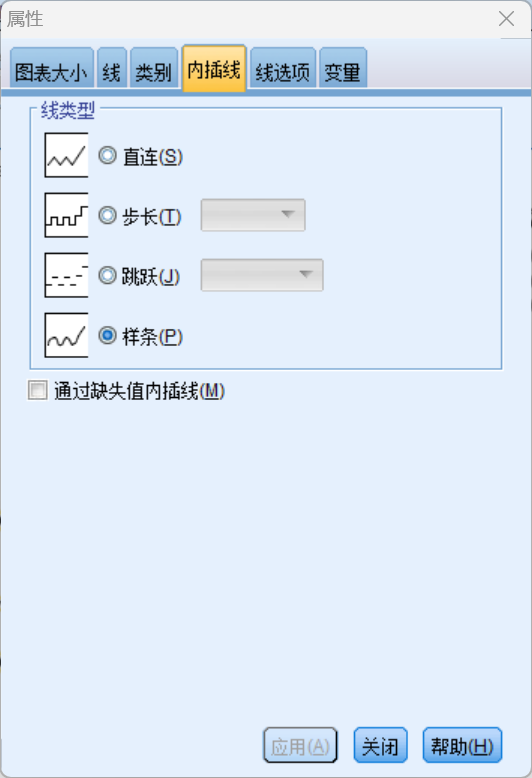
线不够丝滑，设置一下

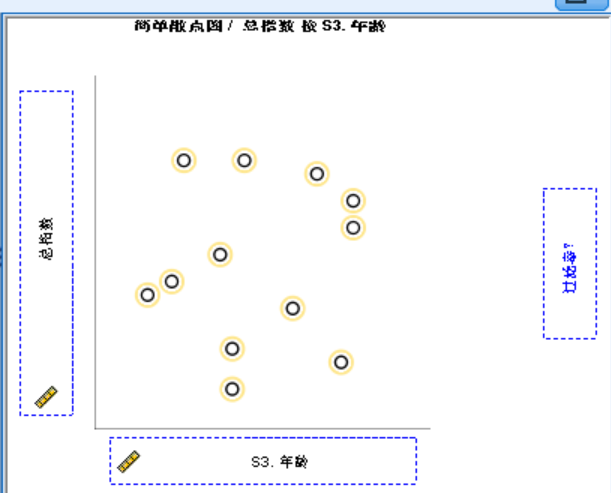
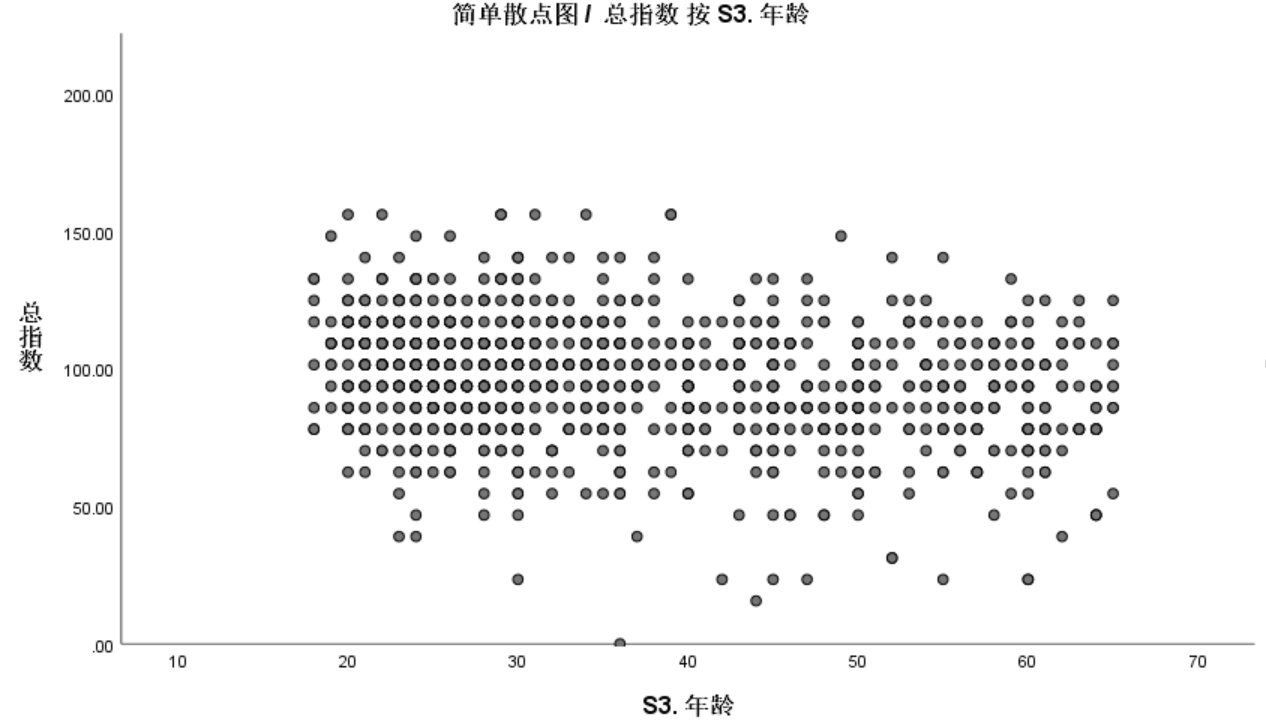
六、散点图

七、P-P图和Q-Q图

在"分析”-->  "描述统计"菜单

如果数据服从 正态分布.则其 中的数据 应和理论直线(对角线)基本重合  可见 ind ex1  的实际分布和理论 分布基本接近。 为了进行更仔细的观察 可以继续观察右侧的去势 p-p 图，该图反映的是按

正态分布计算的理论值和实际值之量的分布情况，即分布的残差图。

如果数据服从正态分 布，则数据点应较均匀地 分布在 y= 0 这条直线上下 ，可能 可见残差虽然有 一 定的 上下波动，但绝对差异均小于 0.05 ，这在绝大多数研究中都是可以想略的分布概率差异。

 不符合正态分布的例子：

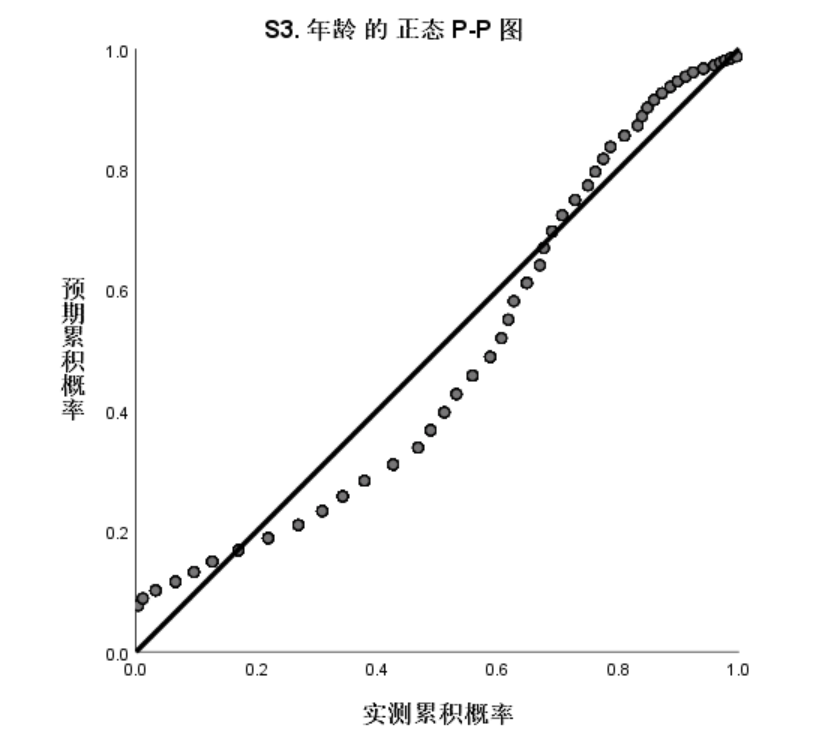
P-P图比较的是两者的累计概率分布 而Q-Q图 则是  根据变量的实际百分位 数与理论百分位数进行绘制的 或者说得更通俗一 点，相比之下 Q-Q 图 的适用条件更宽松，结果也更稳健一些。

八、控制图

"分析'→"质量控制“

九、Pareto图

---

总结

本章主要针对SPSS常用统计图

主要解决问题：

1）使用SPSS完成对常用统计图的表示