数学算法笔记

1、平方差

[蓝桥杯 2023 省 A] 平方差 - 洛谷

考虑将公式化简，然后看x是由什么性质的数组成，该题中，从x奇偶性质入手，判断x可能的组成情况。

题解：Welcome - Luogu Spilopelia

2、完全平方数

[蓝桥杯 2021 省 AB2] 完全平方数 - 洛谷

P8754 [蓝桥杯 2021 省 AB2] 完全平方数 题解 - 洛谷专栏

解题关键：

1）唯一分解定理，对于任意一个数 n，它都可以分解为若干个质数的乘积

2）质因数分解，将一个数分解为若干个质数的乘积

	// n是被分解的数
    for(ll i=2;i*i<=n;i++){
		if(n%i==0) cnt++;
		while(n%i==0){
			p[cnt]=i;//p是质因子
			g[cnt]++;//g是这个质因子的指数
			n/=i;
		}
	}
	if(n>1){
		p[++cnt]=n;
		g[cnt]++;
	}

3、杨辉三角

[蓝桥杯 2021 省 B] 杨辉三角形 - 洛谷

题解：P8749（杨辉三角） - Luogu Column

性质1：杨辉三角中的任何数都可以用层数和对角线数的组合数来表示

性质2：杨辉三角中对角线开头的元素（杨辉三角每层最中间的元素）均比对角线后面的元素小

思路：去找第一个小于n的对角线开头元素，在这条对角线上找利用二分来找n，由于对角线已确定，只需要去二分层数

4、裴蜀定理

[蓝桥杯 2017 省 AB] 包子凑数 - 洛谷

P8646 [蓝桥杯 2017 省 AB] 包子凑数 题解 - 洛谷专栏

5、埃氏筛

把范围n内的素数（质数）筛选出来：从2开始，将每个质数的倍数都标记成合数，直至遍历到n

for(int i=2;i<=N;i++){
    if(!isprime[i]){     
        for(int j=i*i;j<=N;j+=i){
            isprime[j]=1;
        }
    }
}
// 最终isprime为0的数为素数

该算法思想还可用于求数组中所有存在的倍数，相关题目： [蓝桥杯 2022 国 B] 齿轮 - 洛谷

	// vis[]=1表示数组中存在的元素
    for(int i = 1; i <= MAX; i++){
		if(vis[i]){ 
			for(int j = 2*i; j <= MAX; j += i){
				if(vis[j]) ans[j/i] = 1;
			}
		}
	}

6、费马小定理

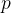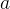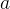若 是质数，设整数 ，则有   ≡  (mod )。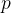

7、gcd & gbs

求最大公约数

int gcd(int a, int b){
	if(a < b){
		int tmp = a;
		a = b;
		b = tmp;
	}
	if(b == 0) return a;
	else return gcd(b, a%b);
}

求最小公倍数

int gbs(int a, int b){
	return a*b/gcd(a,b);
}

8、组合数

如果题目需要用到组合数，若知道组合数a的范围，则可以根据这个公式预处理出全部的组合数。

for(int i = 0; i < N; ++i){
	for(int j = 0; j <= i; ++j){
		if(!j || !i) c[i][j] = 1;
		else c[i][j] = c[i-1][j-1] + c[i-1][j];
	}
}

或者用函数计算

int C(int b, int a) // 计算组合（b在上面，a在下面）
{
    int sum = 1;
    for (int i = a, j = 1; j <= b; i--, j++)
        sum = sum * i / j;
    return sum;
}