递归解决汉诺塔问题（原理图解+代码实现+递归讲解）

话不多说，我们直奔主题

1.递归算法的基本模式：终止条件+递推公式

int digui(int n)
{
	if (sth1)//sth1为终止条件
	{
		return sth2;//sth2通常为一个逻辑上很简单的值
	}
    else
    {
        return sth3;//sth3为递推公式，亦即规律
        //当然这只是一个简单的逻辑，格式上不能拘泥于此
    }
	
}

以递归实现斐波那契数列为例

1，1，2，3，5，，，  f(n)=f(n-1)+f(n-2)，，，

终止条件即 当情况很简单时可以直接得到值，一般是n=1的情形，这时不需要再往下递归了，就算终止了哈哈

此处即 n<=2 时f(n)=1。所以

sth1: n<=2

sth2: 1

递推公式可以理解为我想得到f(n)的值，那我只需要得到f(n-1)+f(n-2)的值；如果我想得到f(n-1)的值，那么我只需要得到f(n-2)+f(n-3)的值。。。直到终止条件

此处即 sth3: f(n-1)+f(n-2)

完整代码

int feiBoNaQie(int n)
{
	if (n <= 2)
	{
		return 1;
	 }
	else
		return feiBoNaQie(n-1)+feiBoNaQie(n-2);
}

 2汉诺塔问题

我们先构建一个基本模型

有a b c三根柱子，初始时先定义a from;b mid;c to。我们的目标就是将a柱上的n个圆盘按照汉诺塔的规则移动到c柱上

 需要解释的是，from,mid,to是对于一个圆盘（或多个圆盘的整体）来说的，比如一个圆盘想从b柱到达c柱，那么对于该圆盘来说b柱为from柱，c柱为to柱，a柱为mid柱。

我们先看看有1，2个盘子的情形，显然

n=1;

a->c

n=2;

a->b  

a->c  

b->c

我们可以这样考虑:

n=2时，我们是先把第一个圆盘放在了mid柱(b),这样对a柱来说，就变成了只有一个盘子的汉诺塔问题,即从from柱(a)-->to柱(c);对于b柱来说，也变成了只有一个盘子的汉诺塔问题，即从from柱(b)->to柱(c）

   --->  

    --->      

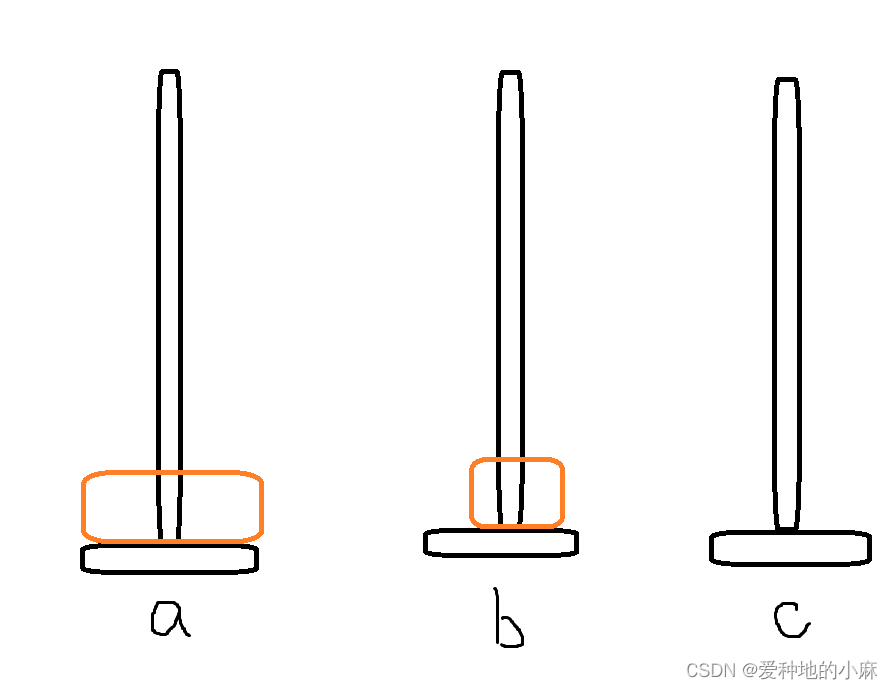
这样我们就先找到了递归的终止条件：

当某柱上只有一个圆盘时，我们仅需将它从from柱移到to柱，注意此时的from柱不一定是a柱，to柱也不一定是c柱，从n==2的分析中我们应该就能看出端倪。

那么递归函数里的终止条件代码就可以这么写：

if(n==1)
{
    printf("%c-->&c\n",from,to);
}

代码里的from,to是代表a,b,c柱子的变量，但是我们目前也不知道对应关系哈哈，但是n肯定是圆盘的数量。

那么递推公式是什么？

当有两个圆盘时我们是把上面那个放在mid柱子，那有n个时我们仍当作两个处理。

1.把上面n-1个当作一个整体，放在mid柱子，

2.a柱一个圆盘放到c柱，

3.b柱n-1个圆盘(此时当作整体)放到c柱。

 

 

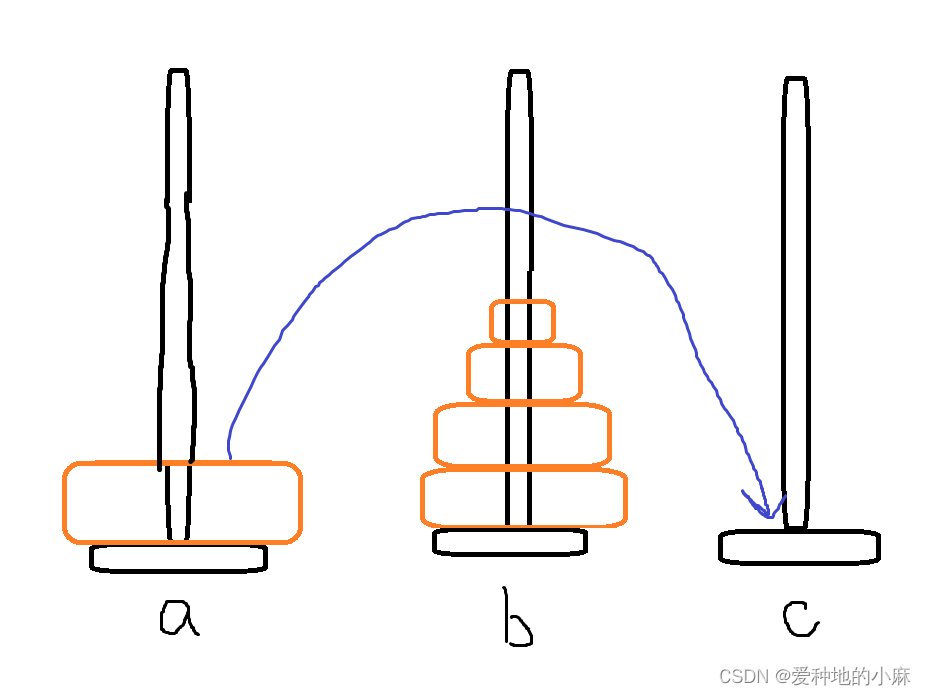
 对a柱上面的n-1个圆盘：a柱是from柱子，b柱是to柱子，c柱子是mid柱子；

对a柱下面的一个圆盘：a柱是from柱子，c柱子是to柱子，b柱是mid柱子；

所以现在的问题就变成了如何将上面n-1个圆盘放到b柱子上面

那么我们继续将这n-1个圆盘划分成两份，上面n-2个，下面一个。

按照两个圆盘的套路，我们要把上面n-2个移到mid柱子。思考，这时的mid柱子是哪根？？

 还是b柱吗？答案是c柱。读者在这里可以先细想下是为什么？？？我就不解释了。。。

。。。

读者应该品出来递归的味道了吧

ok我们总结下n个盘子的规律

对于n 个盘子a-->c mid=b  需要三步：

1.先n-1个盘子a-->b mid=c

2.然后最下面那个盘子a->c mid=b,

3.最后n-1个盘子b-->c mid=a

对于n-1个盘子 a-->b  mid=c 需要三步：

1.先n-2个盘子a-->c mid=b

2.然后最下面那个盘子 a->b mid=c

3.最后n-2个盘子c-->b mid=a

。。。

然后就如此递归下去直到终止条件

并可以发现，

这两句话的第一步 from=上一层（盘子数＋1）的from, to=上一层的mid, mid=上一层的to

                  第二步 from=上一层的from,to=上一层的to,mid=上一层的mid

                  第三步 from=上一层的mid, to=上一层的to,mid=上一层的from

所以这就是递归规律

所以我们假定递归函数

void digui(int n, char from,char mid,char to);

//声明

那么

对于n个圆盘的汉诺塔

要想digui(n,from,mid,to);

那么先 digui(n-1,from,to,mid)

然后 print("%c-->%c\n",from,to)

最后 digui(n-1,mid,to,from)

所以递归函数是

void digui(int n, char from, char mid, char to)
{
    if(n==1)
        printf("%c-->%c\n",from,to);
    else
    {
        digui(n-1,from,to,mid);
        printf("%c-->%c\n",from,to);
        digui(n-1,mid,from,to);
    }
}

作者水平有限，不太能很好地表达自己的想法。如有疑问或纰漏请不吝指教

求个关注和点赞吧  >--<

               

                        。。。