315. 计算右侧小于当前元素的个数
给你一个整数数组
nums,按要求返回一个新数组counts。数组counts有该性质:counts[i]的值是nums[i]右侧小于nums[i]的元素的数量。示例 1:
输入:nums = [5,2,6,1] 输出:[2,1,1,0] 解释: 5 的右侧有 2 个更小的元素 (2 和 1) 2 的右侧仅有 1 个更小的元素 (1) 6 的右侧有 1 个更小的元素 (1) 1 的右侧有 0 个更小的元素示例 2:
输入:nums = [-1] 输出:[0]
示例 3:
输入:nums = [-1,-1] 输出:[0,0]
提示:
1 <= nums.length <= 10(5)
-10(4) <= nums[i] <= 10(4)
题目解题思路
1.
给我们一个nums数组,例如,5,2,6,1。需要填写count数组,并返回。count数组的意思是,count[i]表示nums[i]元素右边有多少个小于自己的元素。
不妨假设我们当前位置是i位置,思考如何填写count[i]的值。
如果我们直接遍历后面的元素,计数有多少个小于自己的元素,初步估计时间复杂度是O(n^2)。
nums.length最大值是10^5。O(n^2)计算出次数是10^10次。
大多数在线编程平台(如 LeetCode, Codeforces, HackerRank 等)通常对每个测试用例设置了时间限制,这个限制一般在 1 到 2 秒之间。这意味着你的代码需要在这个时间范围内完成计算并输出结果。
操作数量:(10^{10}) 操作对应于 10,000,000,000 次迭代或方法调用,这是一个相当大的数字。
单次操作耗时:在标准桌面或服务器处理器上,每秒可以执行大约 (10^8) 到 (10^9) 个简单操作(这取决于操作的复杂性和处理器的性能)。这意味着理论上,(10^{10}) 操作至少需要 10 到 100 秒才能完成,远远超出了大多数在线评测系统的标准时间限制。
因此对于10^10次的代码我们应该认为一定会超时,而不去写这样的代码。
2.
继续思考如何计算count[i]的数值。我们希望计算右边比自己小的数,遇到的问题是我不知道右边哪些数比我小,那些数比我大,所以我必须每个数都遍历,然后去判断是不是比我小。这才是问题本身。
如果我们可以不去比较,直接判断那些数比我小那些数比我大,我们就可以以更快的方式得到答案。
如何不去比较得出一些数与我的大小的比较?很简单,只需要排序就可以了。
如果把一些数进行升序排序,那么左边的数就是比我小的数,这是显而易见的。
我想要找右边比我小的数的个数,那么只需要把所有数排序,用一个count数组记录右边数的个数即可。
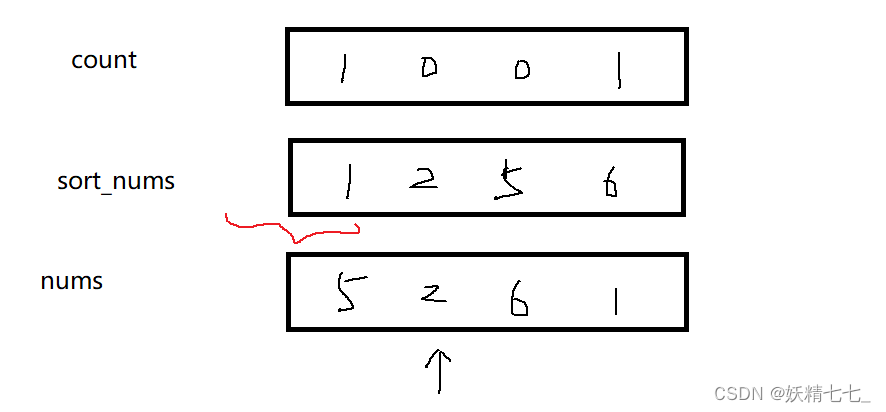
当我i==2的时候,右边数1、6分别出现一次,在count里面记录,只需要遍历sort_nums小于2的区域计数即可,问题就转变为动态前缀和。此时问题是如何解决count与sort_nums下标绑定的问题。
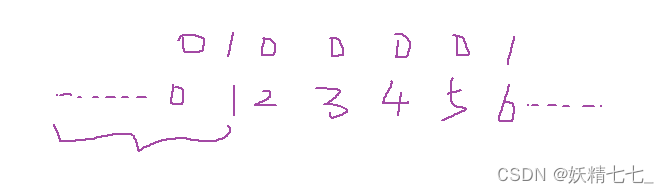
如果以sort_nums为下标,会发现小于0的部分没办法当作是下标。
我们只需要让count数组和sort_nums一一绑定就可以了,当然可以再绑定一个下标,让这三者同时绑定在一起。
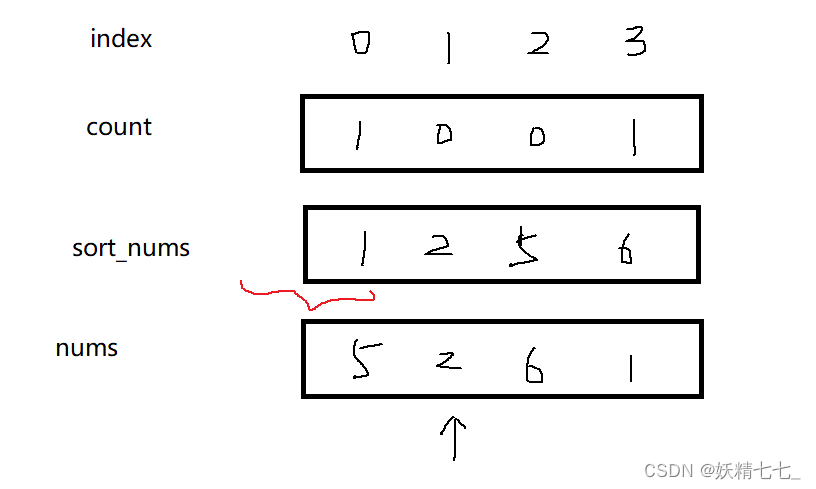
此时我们需要一个map,用于快速查找nums[i]==2对应的下标1,然后通过下标1去找count 0~1-1区间和。
问题就真正变成动态查找 0~i-1区间前缀和+单点更新count数组。
3.
于是我们的解题思路是,从后往前遍历nums数组,i位置,首先通过map查找i位置nums对应的下标index,然后计算0~index-1 count区间和,填写到ret数组i位置。
然后把nums[i]对应index位置count值++。
暴力求解动态前缀和(超时)
暴力求解动态前缀和,每一次用for循环计算0~index-1区间count值,初略估计时间复杂度也是O(n),根据前面的计算还是会超时,但是还是把题解写了,因为这涉及到多个数组绑定+问题转化。如果能够把心中的想法用代码实现即使是超时也是有意义的。
class Solution {
public:
vector<int> countSmaller(vector<int>& nums) {
vector<int> ret(nums.size()); // 创建一个和输入数组同样大小的数组ret,用来存放结果
vector<int> count_nums(nums.size()); // 创建一个计数数组,用来记录每个元素出现的次数
map<int, int> nums_index; // 创建一个map,用来存储每个数和其对应的索引
// 遍历输入数组,初始化map,为每个数分配一个映射,但暂时不分配具体的索引值
//因为我需要用map的特性先排序
for (auto& x : nums) {
nums_index[x];
}
int index = 0; // 索引初始化为0
// 为map中的每个元素分配一个连续的索引,按照从小到大的顺序
//排序排好了就依次添加索引
for (auto& x : nums_index) {
x.second = index++;
}
// 从数组的最后一个元素向前遍历
for (int i = nums.size() - 1; i >= 0; i--) {
int idx = nums_index[nums[i]]; // 获取当前元素的索引
count_nums[idx]++; // 更新当前元素的计数
int sum = 0; // 初始化sum,用于计算小于当前元素的个数
// 遍历当前元素索引左边的所有元素,累加它们的计数,得到小于当前元素的数量
for (int j = 0; j < idx; j++) {
sum += count_nums[j];
}
ret[i] = sum; // 将计算结果存储到结果数组中
}
return ret; // 返回结果数组
}
};
IndexTree求解动态前缀和
利用IndexTree求解动态一维前缀和是非常好的办法。
首先IndexTree解决的问题就是动态前缀和,动态区间和查询,每一次查询时间复杂度非常快。
唯一的缺陷是没办法做到区间更新,只能做到单点更新。但是这道题目就是单点更新+动态前缀和,完美契合IndexTree。
IndexTree的代码也比较简洁。
class IndexTree {
private:
int size; // 树状数组的大小
vector<int> tree; // 用于存储树状数组的数据结构
// 计算x的二进制表示中最低位的1及其后面的0组成的数值
int lowbit(int i) { return i & -i; }
// 在树状数组中的指定位置index加上值c
void _add(int index, int c) {
while (index < size) {
tree[index] += c;
index += lowbit(index);
}
}
// 计算从数组起始到index的前缀和
int _sum(int index) {
int ret = 0;
while (index > 0) {
ret += tree[index];
index -= lowbit(index);
}
return ret;
}
public:
// 构造函数,初始化树状数组的大小和容器
IndexTree(int n) {
size = n + 1; // 因为树状数组的索引从1开始
tree.resize(size);
}
// 对外暴露的添加数据的接口,对应的数组位置加1,因为索引从1开始
void add(int index, int c) { _add(index + 1, c); }
// 对外暴露的计算前缀和的接口,计算前缀和到index,因为索引从1开始
int sum(int index) { return _sum(index + 1); }
// 计算区间[left, right]的和
int range(int left, int right) { return sum(right + 1) - sum(left); }
};
class Solution {
public:
vector<int> countSmaller(vector<int>& nums) {
IndexTree t(nums.size()); // 创建一个树状数组实例,大小与nums相同
map<int, int> nums_index; // 映射每个数到一个唯一的索引
for (auto& x : nums)
nums_index[x]; // 为nums中的每个元素在map中创建键
int inx = 0;
// 为map中的每个元素(即nums的去重排序版本)分配一个递增的索引
for (auto& x : nums_index)
x.second = inx++;
vector<int> counts(nums.size()); // 创建结果数组,用于存储每个元素右侧小于它的元素数量
for (int i = nums.size() - 1; i >= 0; i--) {
int index = nums_index[nums[i]]; // 获取当前元素的索引
counts[i] = t.sum(index - 1); // 计算当前元素之前(即索引更小的元素)的累加和
t.add(index, 1); // 在树状数组中,当前元素的位置加1
}
return counts; // 返回结果
}
};
线段树求解动态前缀和(重新写一遍)
利用线段树求解动态前缀和查询以及单点更新。‘
暴力求解前缀和查询每一次都是O(N),如果是静态的前缀和查询只需要利用前缀和数组即可时间复杂度是O(1)。
但是动态前缀和查询,每一次更新数据对前缀和数组会造成影响,没办法直接使用前缀和数组计算。
但是线段树可以求解动态前缀和查询以及单点更新操作。
线段树相较于IndexTree代码会多许多。优势是可以快速解决区间和更新操作。
class SegmentTree2 {
public:
int MAXN; // 数组的最大长度
vector<int> arr; // 原始数据数组
vector<int> sum; // 线段树的节点值,用于存储区间和
vector<int> lazy; // 延迟更新数组,用于优化区间更新操作
// 构造函数,初始化线段树
SegmentTree2(vector<int> origin) {
MAXN = origin.size() + 1;
arr.resize(MAXN);
for (int i = 1; i < arr.size(); i++)
arr[i] = origin[i - 1];
sum.resize(MAXN << 2);
lazy.resize(MAXN << 2, 0); // 初始化lazy数组为0
}
// 向上更新节点值,用于构建树或者更新后修正父节点的值
void pushUp(int rt) {
sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}
// 构建线段树,l和r表示当前节点覆盖的区间,rt表示当前节点在数组中的位置
void build(int l, int r, int rt) {
if (l == r) {
sum[rt] = arr[l];
return;
}
int mid = (l + r) >> 1;
build(l, mid, rt << 1);
build(mid + 1, r, rt << 1 | 1);
pushUp(rt);
}
// 查询区间[L, R]的和,l和r表示当前节点覆盖的区间,rt为当前节点位置
long query(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
return sum[rt];
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
long ret = 0;
if (L <= mid) {
ret += query(L, R, l, mid, rt << 1);
}
if (R > mid) {
ret += query(L, R, mid + 1, r, rt << 1 | 1);
}
return ret;
}
// 区间添加值函数,为[L, R]区间的每个元素增加C
void add(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
sum[rt] += C * (r - l + 1);
lazy[rt] += C;
return;
}
int mid = (l + r) >> 1;
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
add(L, R, C, l, mid, rt << 1);
}
if (R > mid) {
add(L, R, C, mid + 1, r, rt << 1 | 1);
}
pushUp(rt);
}
// 向下传递更新信息,将当前节点的更新信息传递给其子节点
void pushDown(int rt, int ln, int rn) {
if (lazy[rt] != 0) {
lazy[rt << 1] += lazy[rt];
sum[rt << 1] += lazy[rt] * ln;
lazy[rt << 1 | 1] += lazy[rt];
sum[rt << 1 | 1] += lazy[rt] * rn;
lazy[rt] = 0;
}
}
};
class Solution {
public:
vector<int> countSmaller(vector<int>& nums) {
vector<int> ret(nums.size());
set<int> nums_set; // 使用集合对元素进行去重和排序
for (auto x : nums)
nums_set.insert(x);
vector<int> nums_set_now(nums_set.begin(), nums_set.end());
vector<int> count_nums(nums_set_now.size());
unordered_map<int, int>nums_index; // 为每个元素创建一个唯一索引
for (int i = 0; i < nums_set_now.size(); i++)
nums_index[nums_set_now[i]] = i;
SegmentTree2 segTree(count_nums); // 使用去重并排序后的元素初始化线段树
segTree.build(1, count_nums.size(), 1); // 构建线段树
for (int i = nums.size() - 1; i >= 0; i--) { // 从数组的最后一个元素开始
int index = nums_index[nums[i]]; // 获取当前元素的索引
segTree.add(index + 1, index + 1, 1, 1, count_nums.size(), 1); // 在线段树中,增加当前元素的计数
int sum = 0;
if (index > 0) {
sum = segTree.query(1, index, 1, count_nums.size(), 1); // 查询当前元素之前的所有元素的计数总和
}
ret[i] = sum; // 将查询到的计数总和作为结果存入返回数组
}
return ret; // 返回结果数组,每个元素表示对应位置元素右侧小于该元素的数量
}
};
699. 掉落的方块
在二维平面上的 x 轴上,放置着一些方块。
给你一个二维整数数组
positions,其中positions[i] = [left(i), sideLength(i)]表示:第i个方块边长为sideLength(i),其左侧边与 x 轴上坐标点left(i)对齐。每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落,直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆,它就会固定在原地,无法移动。
在每个方块掉落后,你必须记录目前所有已经落稳的 方块堆叠的最高高度 。
返回一个整数数组
ans,其中ans[i]表示在第i块方块掉落后堆叠的最高高度。示例 1:
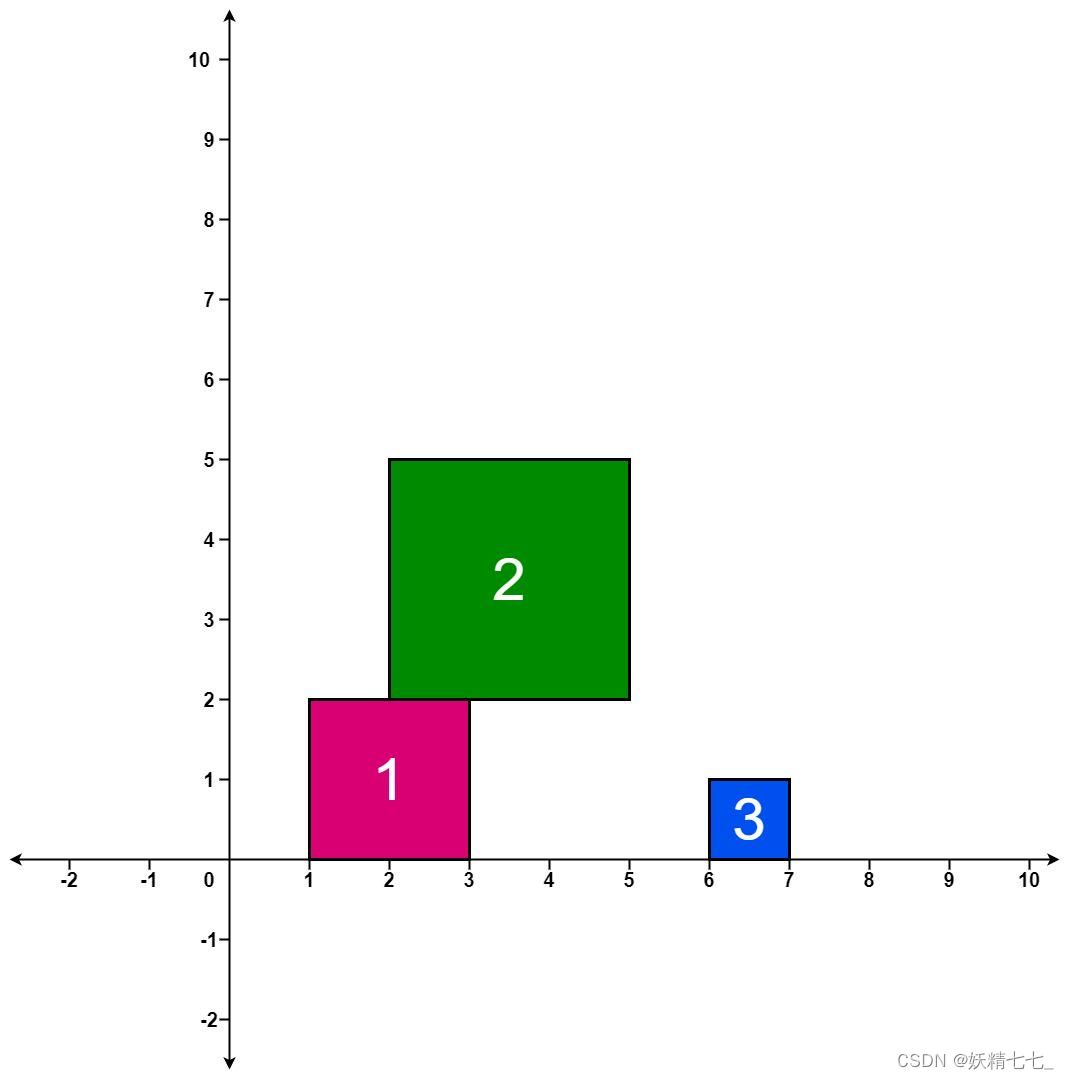
输入:positions = [[1,2],[2,3],[6,1]] 输出:[2,5,5] 解释: 第 1 个方块掉落后,最高的堆叠由方块 1 组成,堆叠的最高高度为 2 。 第 2 个方块掉落后,最高的堆叠由方块 1 和 2 组成,堆叠的最高高度为 5 。 第 3 个方块掉落后,最高的堆叠仍然由方块 1 和 2 组成,堆叠的最高高度为 5 。 因此,返回 [2, 5, 5] 作为答案。
示例 2:
输入:positions = [[100,100],[200,100]] 输出:[100,100] 解释: 第 1 个方块掉落后,最高的堆叠由方块 1 组成,堆叠的最高高度为 100 。 第 2 个方块掉落后,最高的堆叠可以由方块 1 组成也可以由方块 2 组成,堆叠的最高高度为 100 。 因此,返回 [100, 100] 作为答案。 注意,方块 2 擦过方块 1 的右侧边,但不会算作在方块 1 上着陆。
提示:
1 <= positions.length <= 1000
1 <= left(i) <= 10(8)
1 <= sideLength(i) <= 10(6)
区间压缩
坐标压缩是一种有效的技术,尤其在处理大范围但实际使用数据点稀疏的情况下,可以显著减少内存使用和提升运算效率。这里我将通过几个具体的示例来说明坐标压缩的效果和应用。
示例 1:简单压缩
假设我们有以下方块掉落的位置和大小:
方块列表:[[1, 2], [100000000, 3]]
-
未压缩的情况:
-
需要构建一个能覆盖从1到100000002的线段树(因为第二个方块从100000000开始,长度为3)。
-
这将导致线段树的节点数量非常庞大,因为节点数是线段长度的4倍,即需要大约400,000,000个节点。
-
-
压缩后的情况:
-
收集关键点:{1, 3, 100000000, 100000002}
-
映射到新坐标:{1 -> 0, 3 -> 1, 100000000 -> 2, 100000002 -> 3}
-
构建线段树的范围变为从0到3,大大减少了所需的节点数,只需16个节点即可。
-
示例 2:重叠区域
假设方块的落点有重叠:
方块列表:[[10, 5], [14, 2], [20, 1]]
-
未压缩的情况:
-
线段树需要覆盖从10到20的范围。
-
虽然范围不大,但如果坐标直接用作线段树构建,还是会有一定的空间浪费。
-
-
压缩后的情况:
-
收集关键点:{10, 15, 14, 16, 20, 21}
-
映射到新坐标:{10 -> 0, 14 -> 1, 15 -> 2, 16 -> 3, 20 -> 4, 21 -> 5}
-
只需覆盖从0到5的范围,使用更少的节点即可实现。
-
示例 3:密集数据
如果方块密集落在一小块区域内:
方块列表:[[100, 10], [105, 10], [110, 10]]
-
未压缩的情况:
-
需要一个覆盖100到120的线段树。
-
-
压缩后的情况:
-
收集关键点:{100, 110, 105, 115, 120}
-
映射到新坐标:{100 -> 0, 105 -> 1, 110 -> 2, 115 -> 3, 120 -> 4}
-
映射后只需覆盖0到4的范围,减少了节点的数量。
-
效果说明
通过坐标压缩,实际操作的坐标数量大大减少,从而显著减小了线段树所需的节点数。这样不仅节省了内存,而且由于操作的数据量减少,提高了整体的运算效率。在实际应用中,尤其是涉及到大数据处理的场景,坐标压缩是一种非常有效的优化策略。
解题思路
1.
首先我们有一个position数组,每一个变量是一个vector数组,这个vector数组有两个值,第一个值是方块下落的初始下标,第二个值是方块的底边和高的长度。
每次落下一个方块,然后记录当前情况的最高高度,放到ret数组中,最后返回ret。
如果有两个方块[1,2],[3,1],转化过来第一个方块的高度是2,落下的区间是[1,3],ret.push_back(3),第二个方块的高度是1,落下的区间是[3,4]。ret.push_back(3)。我们发现实际上两个方块不会叠在一起,所以我们不能把1~3的值设置为3,我们可以定义区间[1,1]表示[1,2),意思是1~2的区间长度,[2,1]表示[2,3)意思是2~3的区间长度。
我们需要做的是记录每一个区间的最大值,然后计算当前方块的高度和落下的区间,把这个区间的最大值设置为原先的最大值+当前方块的高度。如果查询整个区间的最大值尾插到ret即可。
用maxcount记录各个区间的最大值。
可以使用坐标压缩,因为我们关注的是最大值,并不关注区间长度,因此我们可以把所有的正方形想象成长方形,底边永远都是1,如果两个方块重叠就叠在一起,不是重叠永远都是紧挨着。
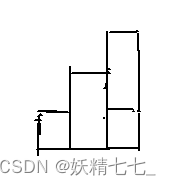
2.
首先用map记录所有需要用到的区间坐标,并且排序。
记录完毕后给map中每一个值映射索引,压缩坐标。
3.
遍历position,每一次获取对应坐标的索引。
[left,right],遍历这个区间找到区间最大值max1,然后维护这个区间的最大值newh=max1+x[1]。
用maxh记录整个区间的最大值,然后维护maxh尾插到ret中。
暴力 查询区间值+更新区间值+坐标压缩
class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
map<int, int> nums_index; // 使用map来存储不同的坐标点,自动排序并去重
vector<int> ret; // 用来存储每个方块掉落后的最高高度结果
// 遍历positions数组,将每个方块的左边界和右边界(左边界+边长-1)加入到map中
for (auto& x : positions) {
nums_index[x[0]];
nums_index[x[0] + x[1] - 1];
}
int index = 0; // 用于给map中的每个唯一坐标点分配一个连续的索引
// 为map中每个坐标点分配索引
for (auto& x : nums_index) {
x.second = index++;
}
vector<int> maxcount(index); // 使用一个数组来记录每个坐标点的当前最大高度
int maxh = INT_MIN; // 记录目前为止所有方块堆叠的最高高度
// 再次遍历positions数组,计算每个方块掉落后的最高堆叠高度
for (auto& x : positions) {
int left = nums_index[x[0]]; // 获取当前方块左边界的索引
int right = nums_index[x[0] + x[1] - 1]; // 获取当前方块右边界的索引
int max1 = INT_MIN; // 用于记录当前方块下方已有方块的最大高度
// 遍历当前方块覆盖的所有索引,找出最大高度
for (int i = left; i <= right; i++) {
max1 = fmax(maxcount[i], max1);
}
int newh = max1 + x[1]; // 计算当前方块掉落后的新高度
// 更新当前方块覆盖的所有索引的高度值
for (int i = left; i <= right; i++) {
maxcount[i] = newh;
}
// 更新全局的最大高度
if (newh > maxh)
maxh = newh;
ret.push_back(maxh); // 将当前的最大高度加入到结果数组中
}
return ret; // 返回结果数组
}
};
线段树+坐标压缩
因为每一次都需要求区间最大值,也就是查询区间值,并且更新区间值,所以可以使用线段树。
class SegmentTree {
private:
vector<int> tree_max; // 线段树数组,存储每个区间的最大值
vector<bool> isupdate; // 懒惰标记数组,标记该区间是否需要更新
vector<int> change; // 如果有更新,记录需要更新的新值
int size; // 线段树管理的原始数据大小
// 向上更新函数,更新父节点的最大值
void pushup(int rt) {
tree_max[rt] = max(tree_max[rt * 2], tree_max[rt * 2 + 1]);
}
// 懒惰传播函数,将当前节点的更新信息传递给子节点
void pushdown(int rt, int ln, int rn) {
if (isupdate[rt]) {
isupdate[rt * 2] = true;
isupdate[rt * 2 + 1] = true;
change[rt * 2] = change[rt];
change[rt * 2 + 1] = change[rt];
tree_max[rt * 2] = change[rt];
tree_max[rt * 2 + 1] = change[rt];
isupdate[rt] = false;
}
}
// 区间更新函数
void update_range(int L, int R, int C, int l, int r, int rt) {
if (L <= l && r <= R) {
isupdate[rt] = true;
change[rt] = C;
tree_max[rt] = C;
return;
}
int mid = (l + r) / 2;
pushdown(rt, mid - l + 1, r - mid);
if (L <= mid)
update_range(L, R, C, l, mid, rt * 2);
if (R > mid)
update_range(L, R, C, mid + 1, r, rt * 2 + 1);
pushup(rt);
}
// 区间查询函数
int query_range(int L, int R, int l, int r, int rt) {
if (L <= l && r <= R) {
return tree_max[rt];
}
int mid = (l + r) / 2;
pushdown(rt, mid - l + 1, r - mid);
int ans = INT_MIN;
if (L <= mid)
ans = max(ans, query_range(L, R, l, mid, rt * 2));
if (R > mid)
ans = max(ans, query_range(L, R, mid + 1, r, rt * 2 + 1));
return ans;
}
public:
SegmentTree(int n)
: size(n), tree_max(4 * n), isupdate(4 * n, false), change(4 * n) {}
void update(int L, int R, int C) { update_range(L, R, C, 1, size, 1); }
int query(int L, int R) { return query_range(L, R, 1, size, 1); }
};
class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
vector<int> result; // 存储每次方块落下后的最大高度
map<int, int> coordCompress; // 坐标压缩映射
// 压缩坐标,将方块的左右边界都映射到一个连续的整数区间
for (const auto& pos : positions) {
coordCompress[pos[0]];
coordCompress[pos[0] + pos[1] - 1];
}
int compressedIdx = 0;
for (auto& coord : coordCompress) {
coord.second = ++compressedIdx;
}
SegmentTree st(compressedIdx); // 初始化线段树
int maxHeight = 0; // 记录当前的最大高度
// 处理每个掉落的方块
for (const auto& pos : positions) {
int left = coordCompress[pos[0]]; // 获取压缩后的左边界
int right =coordCompress[pos[0] + pos[1] - 1]; // 获取压缩后的右边界
int currentHeight = st.query(left, right); // 查询当前区间的最大高度
int newHeight = currentHeight + pos[1]; // 新方块落下后的高度
st.update(left, right, newHeight); // 在区间上更新新的高度值
maxHeight = max(maxHeight, newHeight); // 更新当前已经落稳的方块堆叠的最高高度
result.push_back(maxHeight); // 将当前最大高度添加到结果数组
}
return result; // 返回结果数组,每个元素代表在对应方块掉落后的最高堆叠高度
}
};327. 区间和的个数
给你一个整数数组
nums以及两个整数lower和upper。求数组中,值位于范围[lower, upper](包含lower和upper)之内的 区间和的个数 。区间和
S(i, j)表示在nums中,位置从i到j的元素之和,包含i和j(i≤j)。示例 1:
输入:nums = [-2,5,-1], lower = -2, upper = 2 输出:3 解释:存在三个区间:[0,0]、[2,2] 和 [0,2] ,对应的区间和分别是:-2 、-1 、2 。
示例 2:
输入:nums = [0], lower = 0, upper = 0 输出:1
提示:
1 <= nums.length <= 10(5)
-2(31) <= nums[i] <= 2(31)1
-10(5) <= lower <= upper <= 10(5)题目数据保证答案是一个 32 位 的整数
解题思路
1.
遍历所有区间,利用前缀和数组计算出区间和,比较是否再lower,upper之间内,如果在就ret++。
时间复杂度是O(N^2),最大次数是10^10,显然会超时。但是还是把所思考的代码写出来。
2.
如果我们可以像315. 计算右侧小于当前元素的个数这题一样,遍历一个前缀和后,通过排序直接计算个数就可以简单很多。
lower<=prev[i]-x<=upper ==> prev[i]-upper<=x<=prev[i]-lower
对于一个prev[i]前缀和,只需要看值范围在[prev[i]-upper,prev[i]-lower]范围内的前缀和个数。
问题转化为求处于某个值区间的个数。
让所有可能值排序,然后利用map映射索引,我们就可以找到值对应的索引。
问题转化为求区间和,利用前缀和数组可以求解区间和。
动态区间和,求解完一个prev[i]需要把当前前缀和加入到数组中,单点更新。
区间查询+单点更新,线段树和IndexTree都可以解决。
前缀和+暴力计算(超时)
class Solution {
public:
// 函数接受一个整数数组 nums 以及两个整数 lower 和 upper 作为输入
int countRangeSum(vector<int>& nums, int lower, int upper) {
using LL = long long; // 使用long long类型以支持大整数运算,防止溢出
vector<LL> prevsum(nums.size()); // 创建一个前缀和数组,用于存储从数组开始到当前位置的元素之和
LL sum = 0; // 初始化sum变量,用于计算前缀和
for (LL i = 0; i < nums.size(); i++) { // 遍历数组,计算每个位置的前缀和
sum += nums[i]; // 累加当前元素到sum
prevsum[i] = sum; // 将当前的累计和存储到前缀和数组中
}
LL ret = 0; // 初始化结果变量ret,用于记录满足条件的区间和的个数
for (LL left = 0; left < nums.size(); left++) { // 用两层循环遍历所有可能的子数组(区间)
for (LL right = left; right < nums.size(); right++) { // 内层循环确定子数组的右边界
LL rangesum = prevsum[right] - ((left - 1 >= 0) ? prevsum[left - 1] : 0); // 计算子数组的和
if (rangesum >= lower && rangesum <= upper) ret++; // 如果子数组的和落在[lower, upper]内,则计数加一
}
}
return ret; // 返回满足条件的区间和的个数
}
};
前缀和+线段树+动态区间和
class SegmentTree {
private:
vector<int> sum; // 线段树数组,存储区间和
vector<int> lazy; // 懒惰标记数组,用于区间增加操作
int size; // 线段树管理的元素数量
// 向上更新节点,用于更新父节点的值为其两个子节点的和
void pushup(int rt) {
sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}
// 向下传递懒惰标记,将当前节点的懒惰标记传递给其子节点
void pushdown(int rt, int ln, int rn) {
if (lazy[rt] != 0) {
sum[rt << 1] += lazy[rt] * ln;
sum[rt << 1 | 1] += lazy[rt] * rn;
lazy[rt << 1] += lazy[rt];
lazy[rt << 1 | 1] += lazy[rt];
lazy[rt] = 0;
}
}
// 区间添加操作
void _add(int L, int R, int C, int l, int r, int rt) {
if (r < L || l > R)
return;
if (L <= l && r <= R) {
sum[rt] += C * (r - l + 1);
lazy[rt] += C;
return;
}
int mid = (l + r) >> 1;
pushdown(rt, mid - l + 1, rn - mid); // 下传懒惰标记
_add(L, R, C, l, mid, rt << 1);
_add(L, R, C, mid + 1, r, rt << 1 | 1);
pushup(rt);
}
// 区间查询操作
int _query(int L, int R, int l, int r, int rt) {
if (r < L || l > R)
return 0;
if (L <= l && r <= R) {
return sum[rt];
}
int mid = (l + r) >> 1;
pushdown(rt, mid - l + 1, rn - mid); // 下传懒惰标记
return _query(L, R, l, mid, rt << 1) + _query(L, R, mid + 1, r, rt << 1 | 1);
}
public:
SegmentTree(int _size) : size(_size) {
sum.resize(size << 2);
lazy.resize(size << 2);
}
void add(int L, int R, int C) { _add(L, R, C, 0, size - 1, 1); }
int query(int L, int R) { return _query(L, R, 0, size - 1, 1); }
};
class Solution {
public:
using LL = long long; // 使用long long类型以支持大数运算
int countRangeSum(vector<int>& nums, int lower, int upper) {
map<LL, int> value_index; // 用于坐标压缩的映射
LL sum = 0;
// 初始化坐标压缩映射
for (auto& x : nums) {
sum += x;
value_index[sum];
value_index[sum - lower];
value_index[sum - upper];
}
int inx = 0;
for (auto& x : value_index) {
x.second = inx++;
}
SegmentTree st(inx); // 初始化线段树
int ret = 0;
sum = 0;
for (auto& x : nums) {
sum += x;
// 如果当前前缀和本身就在[lower, upper]范围内
if (sum <= upper && sum >= lower) ret++;
// 计算符合条件的区间和的数量
int left = value_index[sum - upper]; // 计算当前和减去上界后对应的压缩后的索引
int right = value_index[sum - lower]; // 计算当前和减去下界后对应的压缩后的索引
ret += st.query(left, right); // 查询线段树中[left, right]范围内的计数
// 更新线段树,增加当前和的计数
st.add(value_index[sum], value_index[sum], 1);
}
return ret; // 返回满足条件的区间和的总数
}
};
前缀和+IndexTree+动态区间和
class indextree {
private:
using LL = long long; // 使用long long类型以支持大整数运算,避免溢出
LL size; // 1~size-1,树状数组的有效范围
vector<LL> tree; // 树状数组
LL lowbit(LL i) { // 计算lowbit,用于确定更新和查询的范围
return i & -i;
}
void _add(LL index, LL c) { // 内部的添加函数,用于更新树状数组
while (index < size) {
tree[index] += c;
index += lowbit(index);
}
}
LL sum(LL index) { // 计算前缀和,用于区间和查询
LL ret = 0;
while (index > 0) {
ret += tree[index];
index -= lowbit(index);
}
return ret;
}
LL _rangesum(LL left, LL right) { // 内部的范围求和函数
return sum(right) - sum(left - 1);
}
public:
indextree(LL n) { // 构造函数,初始化树状数组的大小
size = n + 1;
tree.resize(size);
}
LL rangesum(LL left, LL right) { // 公开的范围求和接口
return _rangesum(left + 1, right + 1);
}
void add(LL index, LL c) { // 公开的添加接口,用于更新树状数组
_add(index + 1, c);
}
};
class Solution {
public:
using LL = long long; // 使用long long类型以支持大整数运算
int countRangeSum(vector<int>& nums, int lower, int upper) {
vector<LL> prevsum(nums.size()); // 用于存储前缀和
LL sum = 0;
for (LL i = 0; i < nums.size(); i++) { // 计算前缀和数组
sum += nums[i];
prevsum[i] = sum;
}
map<LL, LL> prev_index; // 坐标压缩映射
for (LL i = 0; i < nums.size(); i++) { // 初始化坐标压缩映射
prev_index[prevsum[i]]; // 当前前缀和
prev_index[prevsum[i] - lower]; // 当前前缀和减去lower
prev_index[prevsum[i] - upper]; // 当前前缀和减去upper
}
LL index = 0; // 压缩坐标索引
for (auto& x : prev_index) { // 为每一个前缀和分配一个唯一的索引
x.second = index++;
}
indextree t(prev_index.size()); // 初始化树状数组
LL ret = 0; // 存储满足条件的区间和数量
for (LL i = 0; i < prevsum.size(); i++) { // 遍历每个前缀和
if (prevsum[i] >= lower && prevsum[i] <= upper) ret++; // 如果当前前缀和本身就在范围内
LL left = prev_index[prevsum[i] - upper]; // 计算符合条件的左边界索引
LL right = prev_index[prevsum[i] - lower]; // 计算符合条件的右边界索引
ret += t.rangesum(left, right); // 查询当前满足条件的区间和数量
t.add(prev_index[prevsum[i]], 1); // 在树状数组中记录当前前缀和出现的次数
}
return ret; // 返回满足条件的区间和总数。
}
};结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!























 675
675

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










