
代码:
n = 0:7;
% 信号 x1(n)
x1 = [1,1,1,1,0,0,0,0]; % R4(n)
%信号 x2(n)
x2 = zeros(size(n));
for i = 1:length(n)
if n(i) >= 1 && n(i) <= 3
x2(i) = n(i) + 1;
elseif n(i) >= 4 && n(i) <= 7
x2(i) = 8 - n(i);
end
end
% 信号 x3(n)
x3 = zeros(size(n));
for i = 1:length(n)
if n(i) >= 0 && n(i) <= 3
x3(i) = 4 - n(i);
elseif n(i) >= 4 && n(i) <= 7
x3(i) = n(i) - 3;
end
end
% 信号 x4(n)
x4 = cos(pi/4 * n);
% 信号 x5(n)
x5 = sin(pi/8 * n);
% 信号 x6(t)
t = 0:0.01:1; % 时间范围
x6 = cos(8 * pi * t) + cos(16 * pi * t) + cos(20 * pi * t);
% 绘制信号
figure(100);
subplot(3, 2, 1), stem(n, x1), title('x1(n)');
subplot(3, 2, 2), stem(n, x2), title('x2(n)');
subplot(3, 2, 3), stem(n, x3), title('x3(n)');
subplot(3, 2, 4), stem(n, x4), title('x4(n)');
subplot(3, 2, 5), stem(n, x5), title('x5(n)');
subplot(3, 2, 6), plot(t, x6), title('x6(t)');
实验结果:
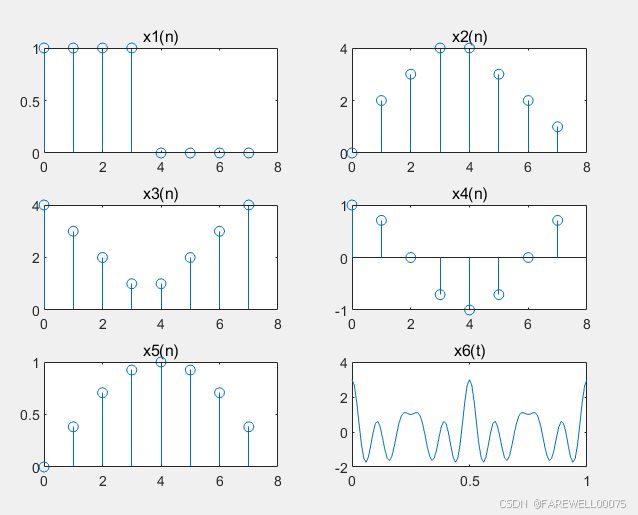
注:这部分可做可不做,感兴趣的自己可以跑一下玩玩
第一题:
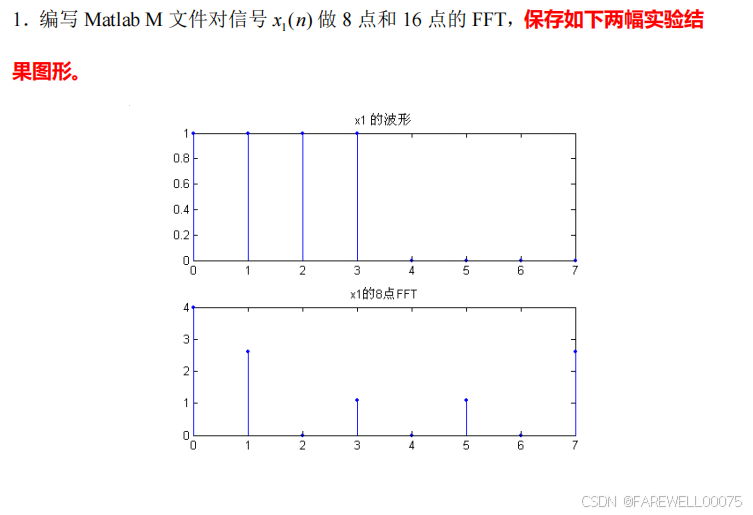
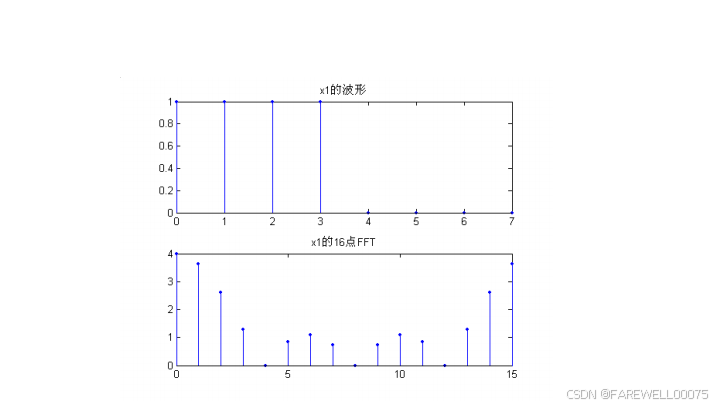
代码:
%第一题
N1=8;
N2=16;
N3=32;
x1=[1,1,1,1,0,0,0,0];
y_1=[1,1,1,1];
xk_1=fft(x1,N1);
yk_1=fft(y_1,N2);
figure(1);
subplot(2,2,1);stem(0:length(x1)-1,x1,'.');title('x1的波形');
subplot(2,2,3);stem(0:N1-1,abs(xk_1),'.');title('x1的8点FFT');
subplot(2,2,2);stem(0:length(x1)-1,x1,'.');title('x1的波形');
subplot(2,2,4);stem(0:N2-1,abs(yk_1),'.');title('x1的16点FFT');
实验结果:
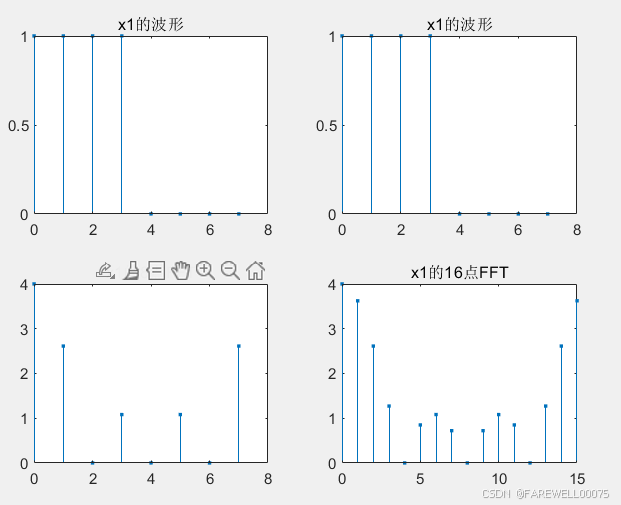
第二题:
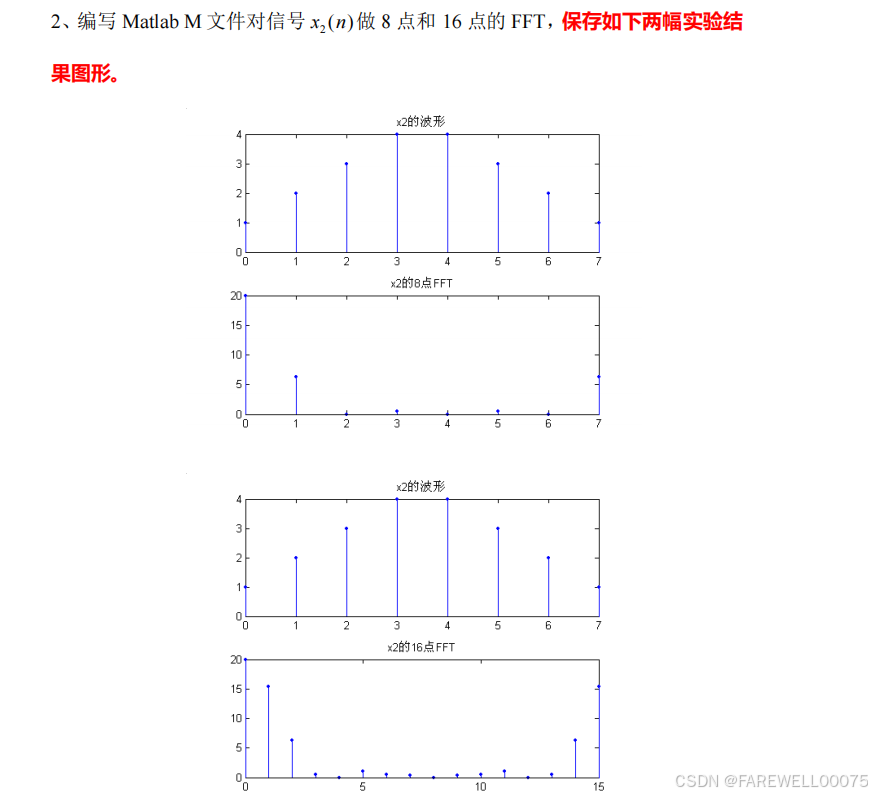
代码:
%第二题
x_2=[1,2,3,4,4,3,2,1];
y_2=[1,2,3,4,4,3,2,1];
xk_2=fft(x_2,N1);
yk_2=fft(y_2,N2);
figure(2);
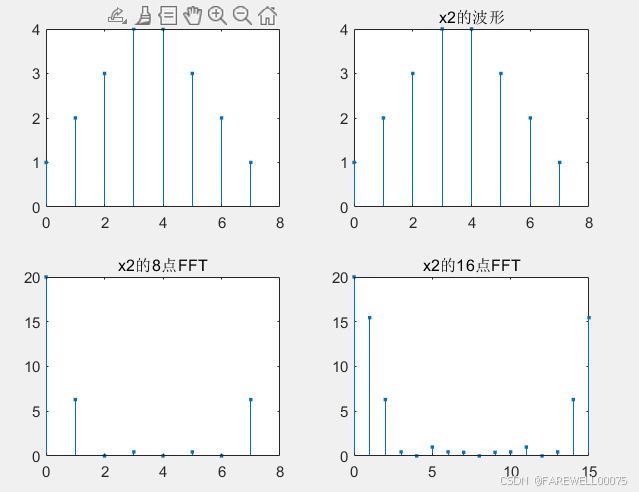
subplot(2,2,1);stem(0:length(x_2)-1,x_2,'.');title('x2的波形');
subplot(2,2,3);stem(0:N1-1,abs(xk_2),'.');title('x2的8点FFT');
subplot(2,2,2);stem(0:length(x_2)-1,x_2,'.');title('x2的波形');
subplot(2,2,4);stem(0:N2-1,abs(yk_2),'.');title('x2的16点FFT');
实验结果:
第三题:
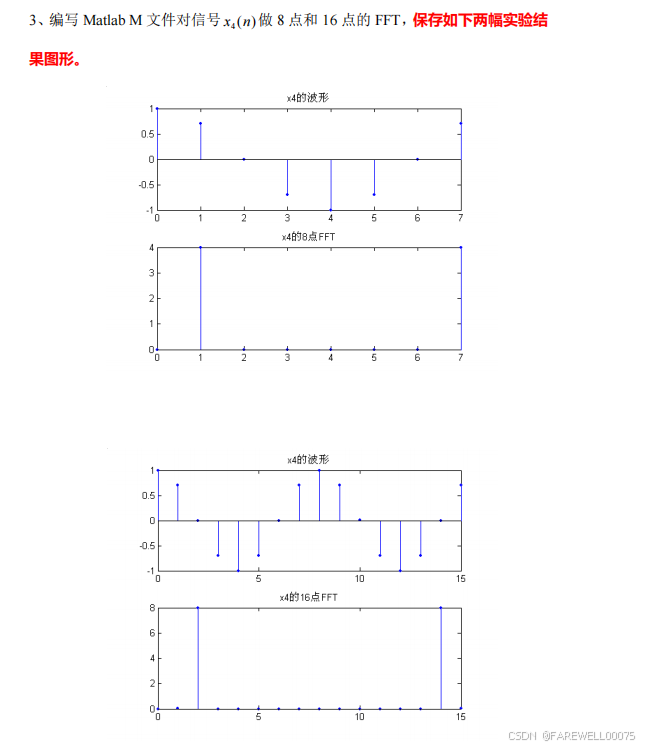
代码:
%第三题
n1=0:7;
x_4=cos(pi/4*n1);
n2=0:15;
y_4=cos(pi/4*n2);
xk_4=fft(x_4,N1);
yk_4=fft(y_4,N2);
figure(3);
subplot(2,2,1);stem(0:length(x_4)-1,x_4,'filled');title('x4的波形');
subplot(2,2,3);stem(0:N1-1,abs(xk_4),'filled');title('x4的8点FFT');
subplot(2,2,2);stem(0:length(y_4)-1,y_4,'filled');title('x4的波形');
subplot(2,2,4);stem(0:N2-1,abs(yk_4),'filled');title('x4的16点FFT');
实验结果:
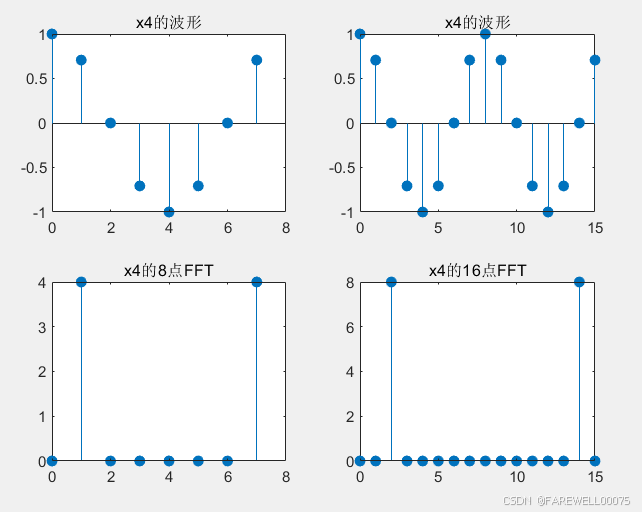
分析:
由题意得周期为8,做的DFT采取的点数为周期8的整数倍,所以所绘制的图像应该是没有问题的。
第三点五题:
做x(5)的FFT
代码:
%第三点五题
n1=0:7;%8点
x_3_5=sin(pi/8*n1);
n2=0:15;%16点
y_3_5=sin(pi/8*n2);
n3=0:31;%32点
z_3_5=sin(pi/8*n3);
xk_3_5=fft(x_3_5,N1);
yk_3_5=fft(y_3_5,N2);
zk_3_5=fft(z_3_5,N3);
figure(9);
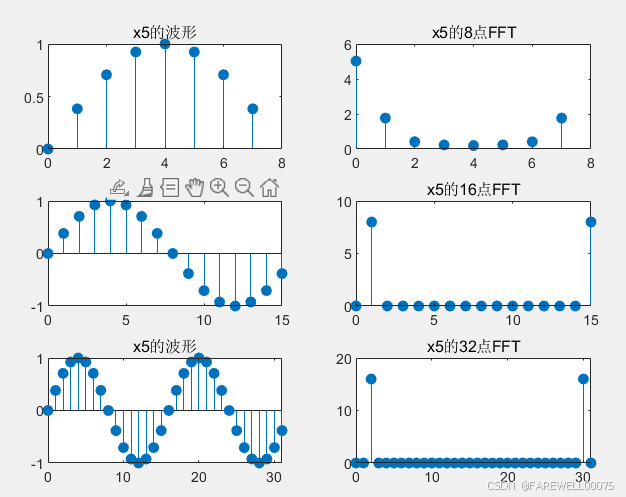
subplot(3,2,1);stem(0:length(x_3_5)-1,x_3_5,"filled");title("x5的波形");
subplot(3,2,3);stem(0:length(y_3_5)-1,y_3_5,"filled");title("x5的波形");%16点
subplot(3,2,5);stem(0:length(z_3_5)-1,z_3_5,"filled");title("x5的波形");%32点
subplot(3,2,2);stem(0:N1-1,abs(xk_3_5),'filled');title('x5的8点FFT');
subplot(3,2,4);stem(0:N2-1,abs(yk_3_5),'filled');title('x5的16点FFT');
subplot(3,2,6);stem(0:N3-1,abs(zk_3_5),'filled');title('x5的32点FFT');
实验结果:
第四题:

代码:
%第四题
N3=32;
N4=64;
n1=0:15;
n2=0:31;
n3=0:63;
fs_64=64;
x_6_1=cos(1/8*pi*n1)+cos(1/4*pi*n1)+cos(5/16*pi*n1);
x_6_2=cos(1/8*pi*n2)+cos(1/4*pi*n2)+cos(5/16*pi*n2);
x_6_3=cos(1/8*pi*n3)+cos(1/4*pi*n3)+cos(5/16*pi*n3);
xk_6_1=1/fs_64*fft(x_6_1,N2);
xk_6_2=1/fs_64*fft(x_6_2,N3);
xk_6_3=1/fs_64*fft(x_6_3,N4);
figure(4);
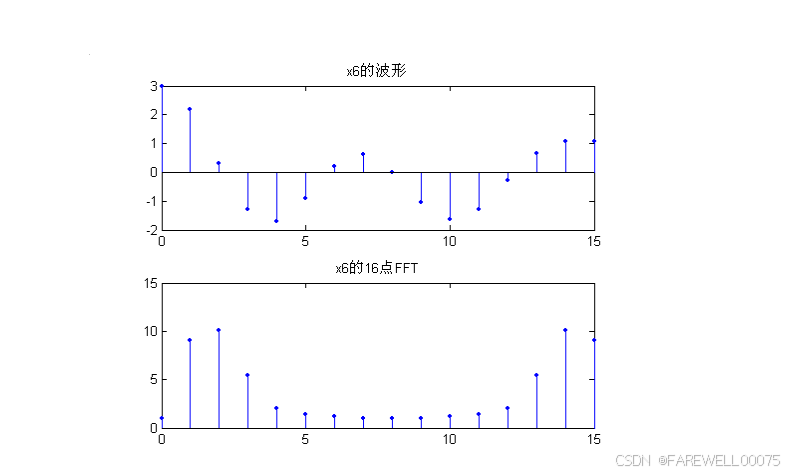
subplot(3,2,1);stem(0:length(x_6_1)-1,x_6_1,'.');title('x6的波形');
subplot(3,2,2);stem(0:N2-1,abs(xk_6_1),'.');title('x6的16点FFT');
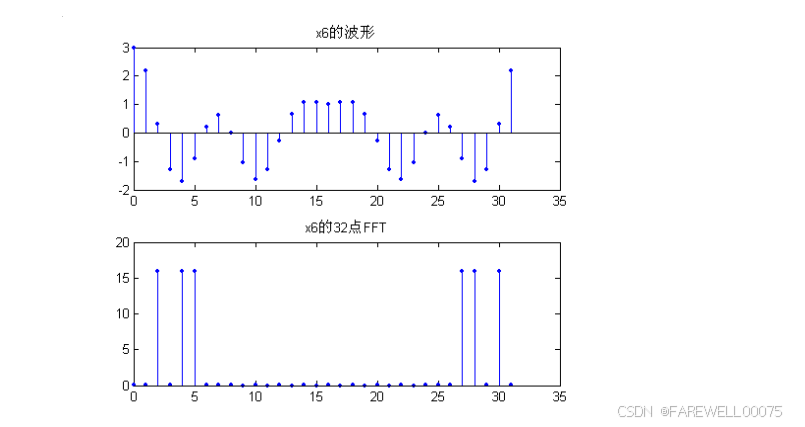
subplot(3,2,3);stem(0:length(x_6_2)-1,x_6_2,'.');title('x6的波形');
subplot(3,2,4);stem(0:N3-1,abs(xk_6_2),'.');title('x6的32点FFT');
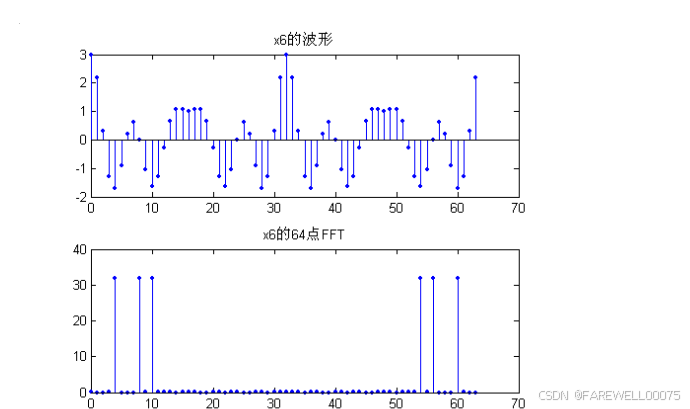
subplot(3,2,5);stem(0:length(x_6_3)-1,x_6_3,'.');title('x6的波形');
subplot(3,2,6);stem(0:N4-1,abs(xk_6_3),'.');title('x6的64点FFT');
实验结果:
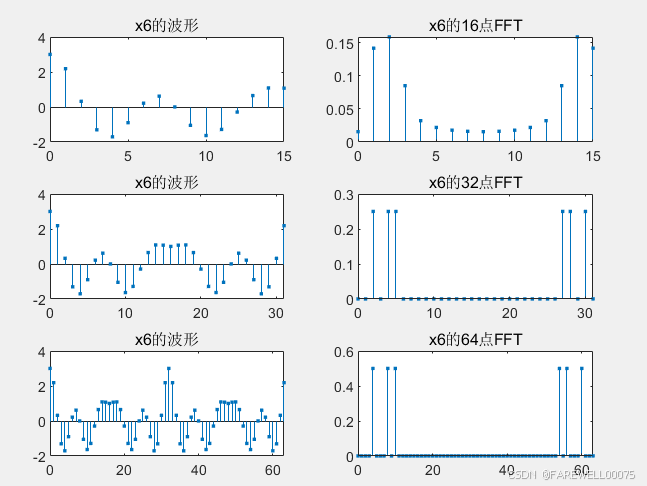
注意:fft后一定要×周期!!!

第五题:

代码:
%第五题
[xn, fs] = audioread('motherland.wav');
x_5= xn(8000:8199);
N_5 = 512;
X = fft(x_5, N_5);
f = (0:N_5-1)*(2*pi/N_5); %f = (0:N_5-1)*(fs/N_5);
M = abs(X);
N_5 = angle(X);
% 绘制幅度谱
figure(5);
subplot(2, 1, 1);
plot(f/pi, M);%plot(f, M);
title('频谱幅度谱(N=512)');
xlabel('角频率/pi (rad/s)');%xlabel('频率 (Hz)')
ylabel('幅度');
grid on;
% 绘制相位谱
subplot(2, 1, 2);
plot(f/pi, N_5);%plot(f/pi, N_5);
title('频谱相位谱(N=512)');
xlabel('角频率/pi (rad/s)');%xlabel('频率 (Hz)')
ylabel('相位 (弧度)');
grid on;
实验结果:
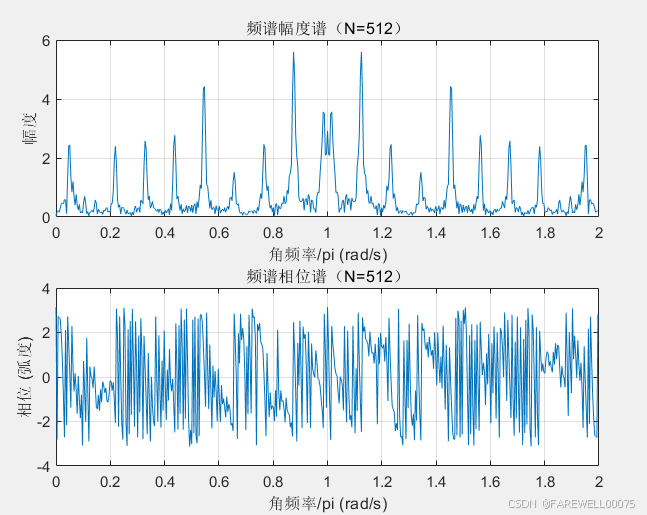
第六题:

注:这个就是直接抄代码,懒得抄的可以直接复制我的
代码:
%第六题
A=imread("lena.bmp");
figure(6);
subplot(311)
imshow(A);
title("原图");
fftI=fft2(A);%二维离散傅里叶变换
A1=abs(fftI);%取模值
%限制幅度在[0,255]
B1=(A1-min(min(A1)))/(max(max(A1))-min(min(A1)))*255;
subplot(312)
imshow(B1);title("二位幅度谱图");
B2=fftshift(B1);
subplot(313)
imshow(B2);title("移到中心位置的二维频谱图");
实验结果:

思考题:
思考题一:
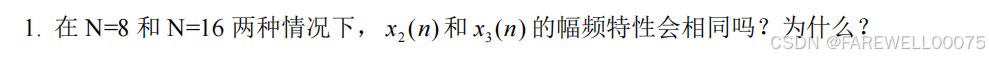
代码:
%思考题一
x_think_1_2=[1,2,3,4,4,3,2,1];
y_think_1_2=[1,2,3,4,4,3,2,1,0,0,0,0,0,0,0,0];
x_think_1_3=[4,3,2,1,1,2,3,4];
y_think_1_3=[4,3,2,1,1,2,3,4,0,0,0,0,0,0,0,0];
xk_think_1_2=fft(x_think_1_2,N1);%N1=8 N2=16
yk_think_1_2=fft(y_think_1_2,N2);
xk_think_1_3=fft(x_think_1_3,N1);
yk_think_1_3=fft(y_think_1_3,N2);
figure(7);
%x2(n)相关
subplot(4,2,1);stem(0:length(x_think_1_2)-1,x_think_1_2,'.');title('x2的波形');
subplot(4,2,3);stem(0:N1-1,abs(xk_think_1_2),'.');title('x2的8点FFT');
subplot(4,2,2);stem(0:length(y_think_1_2)-1,y_think_1_2,'.');title('x2的波形');
subplot(4,2,4);stem(0:N2-1,abs(yk_think_1_2),'.');title('x2的16点FFT');
%x3(n)相关
subplot(4,2,5);stem(0:length(x_think_1_3)-1,x_think_1_3,'.');title('x3的波形');
subplot(4,2,7);stem(0:N1-1,abs(xk_think_1_3),'.');title('x3的8点FFT');
subplot(4,2,6);stem(0:length(y_think_1_3)-1,y_think_1_3,'.');title('x3的波形');
subplot(4,2,8);stem(0:N2-1,abs(yk_think_1_3),'.');title('x3的16点FFT');
实验结果:
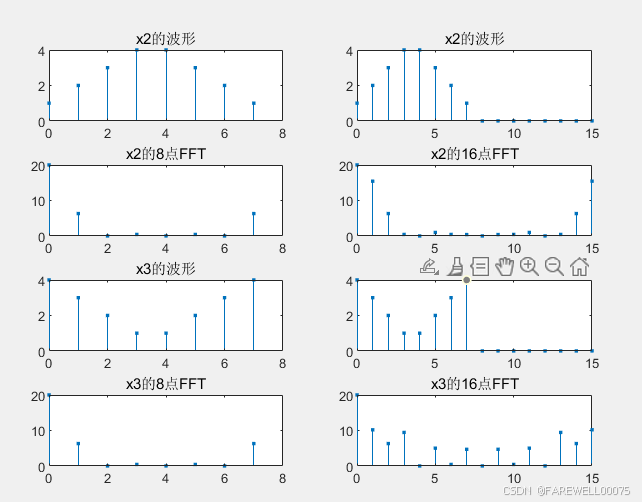
分析:

思考题二:
答:
1.对信号进行fft变换,得到信号的频域表示。
2.在频域中,找到信号的主要频率分量。可以通过观察频谱图或者寻找频域中的峰值来确定信号的主要频率。
3.计算信号的周期。根据周期信号的定义,信号的周期是重复出现的最小时间长度。可以通过信号的主要频率来计算信号的周期。假设信号的主要频率为f,则信号的周期为T=1/f。
4.对信号进行周期扩展。根据信号的周期,将信号进行周期性扩展,使得信号在任意时刻都具有相同的值序列。扩展后的信号称为周期信号。
5.对扩展后的周期信号进行FFT变换,得到信号的频谱图,在频谱图中,可以看到信号的主要频率分量以及其他频率分量,
6.分析频谱图。通过分析频谱图,可以得到信号在不同频率上的分布情况,进一步理解信号的特性
需要注意的是,如果信号中存在多个频率分量,则需要通过多个峰值来确定信号的周期。此外,如果信号是非周期信号,则无法使用FFT进行谱分析。
思考题三

代码:
%思考题三
x_think_3=[1,1,2,2,3,3,2,2,1,1];
%第一小问
%x_think_3_1=[1,2,3,2,1];
x_think_3_1=x_think_3(1:2:end);
%第二小问
x_think_3_2=[1,0,1,0,2,0,2,0,3,0,3,0,2,0,2,0,1,0,1];
%x_think_3_2= zeros(1, 2 * length(x_think_3) - 1); % 创建插入0后的新向量
%x_think_3_2(1:2:end)=x_think_3;
%第三小问
N_think_3=512;
xk_think_3=fft(x_think_3,N_think_3);
xk_think_3_1=fft(x_think_3_1,N_think_3);
xk_think_3_2=fft(x_think_3_2,N_think_3);
f_think_3=(0:N_think_3-1)*(2*pi/N_think_3);%频率
figure(8)
subplot(311);
plot(f_think_3/pi,abs(xk_think_3));
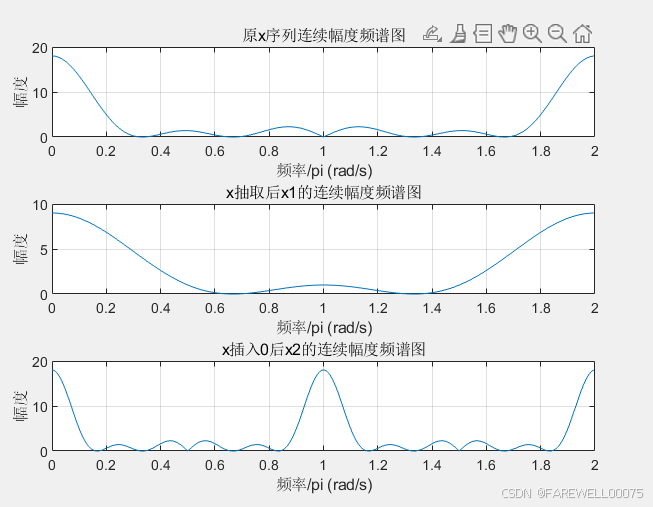
title('原x序列连续幅度频谱图');
xlabel('频率/pi (rad/s)');
ylabel('幅度');
grid on;
subplot(312);
plot(f_think_3/pi,abs(xk_think_3_1));
title('x抽取后x1的连续幅度频谱图');
xlabel('频率/pi (rad/s)');
ylabel('幅度');
grid on;
subplot(313);
plot(f_think_3/pi,abs(xk_think_3_2));
title('x插入0后x2的连续幅度频谱图');
xlabel('频率/pi (rad/s)');
ylabel('幅度');
grid on;
实验结果:
分析:
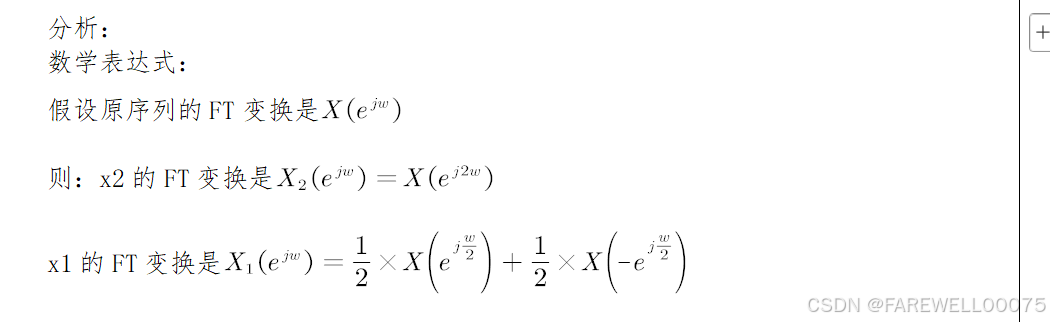
抽取序列x1:
对原序列进行抽取,使得原序列的频谱以二倍频率扩展,而且采样率也会减半。由于频谱被扩展,原始频谱中的低频成分会“拉伸”到高频范围,造成频谱混叠。频谱混叠的结果是,某些低频成分会叠加在高频成分之上,使得高频部分的幅度发生变化。
内插序列x2:
内插操作相当于在时域中增加采样点(零值点),等效于提高采样频率。在频谱压缩的同时,内插导致高频成分的幅度逐渐衰减。这种衰减现象是由零插值引入的,因为在频域中,插入零值会导致频谱中的能量分布更集中,从而在低频区域出现幅度的升高。

























 613
613

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










