扩展欧几里得 及 逆元

• 裴蜀定理

重要推论:a,b互质的充要条件是存在整数x,y使ax+by=1;

• 扩展欧几里得(exgcd)————求ax+by=gcd(a,b)的解

在朴素的求gcd(a,b)的过程中使用递归算法,达到递归边界时 b′=0, a′=gcd(a,b). 可知 a′⋅1 +  b′⋅0 = gcd(a,b),但 a′,b′ 已不是最开始的 a,b. 因此要想求出 x,y, 就要回到最开始的 a,b. 由于是递归算法,所以我们在回溯时考虑如何回到上一层.

若有 ax1​ + by1​ = gcd(a,b) 则有  bx2​ + (a mod b) y2 ​= gcd(b,amodb) 若知道了 x1​,x2​,y1​,y2​间的关系,就能递归运算. 观察 bx2​ + (a mod b)y2 ​= gcd(b,amodb),将 (a mod b)展开. 可写作 bx2​ + ( a − ⌊a/b​⌋⋅b)⋅y2​ 

化简得 ay2​ + b(x2 ​− ⌊a/b​⌋⋅y2​)= gcd(b,a mod b)  ∵gcd(a,b)=gcd(b,a mod b) ∴ 联立可得 x1​=y2​,y1​=x2​−⌊a / b​⌋⋅y2​

已知 x0​=1,y0​=0,则可以求出 ax + by = gcd(a,b) 的一组解x,y

• 如何求通解?

方程 ax + by = gcd(a,b)中 若有常数 k1​,k2​, 将 2x+k1​,y−k2​仍能使方程成立,那么 (x+k1​),(y−k2​)就是一组新解.

a⋅(x+k1​)+b⋅(y−k2​)=gcd(a,b)

 ax+by+ak1​−bk2​=gcd(a,b)

∴ak1​=bk2​

为得到所有解,需满足

ak1​=bk2​=t⋅lcm(a,b)   (t∈Z) ∴ k1​=gcd(a,b)b​, k2​=gcd(a,b)a​

• 对于更一般的情况

 ax+by=c 由裴蜀定理,若 c mod gcd(a,b)!=0,则方程无解 若  gcd(a,b)⋅t=c,只需求出ax+by=gcd(a,b)的解后乘t即可

原理

扩展欧几里得算法是基于欧几里得算法的扩展。欧几里得算法（辗转相除法）用于求解两个整数的最大公约数。但是，扩展欧几里得算法不仅计算最大公约数，还能找到满足贝祖等式 ax + by = gcd(a, b) 的整数解 x 和 y。

算法的基本思想是通过递归调用求解两个整数的最大公约数，并回溯计算整数解。具体步骤如下：

1. 若 b = 0，则 a 是最大公约数，同时设置 x = 1，y = 0。
2. 否则，递归调用扩展欧几里得算法，将 b 和 a % b 作为新的参数传入。
3. 在递归回溯过程中，根据贝祖等式进行解的计算。
4. 成立的条件 ax + by = d;  d 能够整除 gcd(a,b)

int exgcd(int a, int b, int &x, int &y) {
	if (!b) {
		x = 1, y = 0;
		return a;
	}

    // by + (a%b)x = gcd(a,b)
    // by + (a - a/b * b)x = gcd(a,b);
    // 化简  ax + b(y - a/b * x)  = gcd(a,b);
    // 所以 x = y      y = (y - a/b * x)

	int d = exgcd(b, a % b, y, x);
	y -=a / b * x;

	return d;
}

假设我们要求解 a = 20 和 b = 15 的最大公约数，并找到满足贝祖等式 ax + by = gcd(a, b) 的整数解 x 和 y。我们可以进行如下的调用：

int a = 20, b = 15; int x, y; int gcd = exgcd(a, b, x, y);

初始时，a = 20，b = 15，x 和 y 的值不确定。

1. 第一次递归调用 exgcd(20, 15, y, x)：

   • 由于 b = 15 不等于 0，进入递归。
   • 将参数传入为 b = 15 和 a % b = 20 % 15 = 5。
   • 继续递归调用 exgcd(15, 5, x, y)。

2. 第二次递归调用 exgcd(15, 5, x, y)：

   • 由于 b = 5 不等于 0，进入递归。
   • 将参数传入为 b = 5 和 a % b = 15 % 5 = 0。
   • 继续递归调用 exgcd(5, 0, y, x)。

3. 第三次递归调用 exgcd(5, 0, y, x)：

   • 由于 b = 0，到达递归出口。
   • 将 x 赋值为 1，y 赋值为 0。
   • 返回 a = 5 作为最大公约数。

回溯过程：

• 回溯到第二次递归调用：此时 d = 5，将 y 递归得到的值减去 x 的 5/a 倍，即 y -= 5 / 15 * 1 = -1。
• 回溯到第一次递归调用：此时 d = 5，将 x 递归得到的值赋给 y，即 x = -1。
• 回溯到初始调用：此时 d = 5，得到最大公约数 gcd = 5。
• 最终结果：x = -1，y = 0，gcd = 5。

所以，在这个例子中，a = 20 和 b = 15 的最大公约数是 5，同时满足贝祖等式的解为 x = -1，y = 0。

线性同余方程

扩展欧几里得算法可以解决线性同余方程 ax ≡ b (mod m)。通过求解该方程，可以得到同余方程的一个特定解，以及所有解的集合。

乘法逆元

模乘运算中，任意整数 a(mod n)的逆元表示为：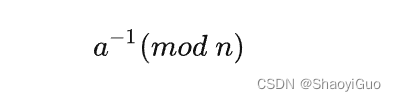

并且根据逆元的定义，满足如下等式：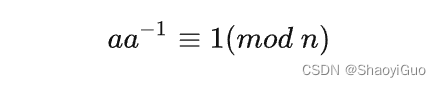 

可以理解成 a 和 a的−1次方 在 n 的作用下发生了反应，变成了 1。 

那么逆元怎么求呢？接下来介绍几种逆元的求解方法：

1.扩展欧几里得定理

 

两个整数相乘等于 1，则他们要么都等于 1，要么都等于 −1，又因为任何两个数的最大公约数不可能为负数，所以 g =1。
    所以当 a 和 b 不互素时，逆元必定不存在，直接返回 −1；
    那么，我们只需要考虑 a 和 b 互素的情况。
    给出以下推导式：

 求逆元

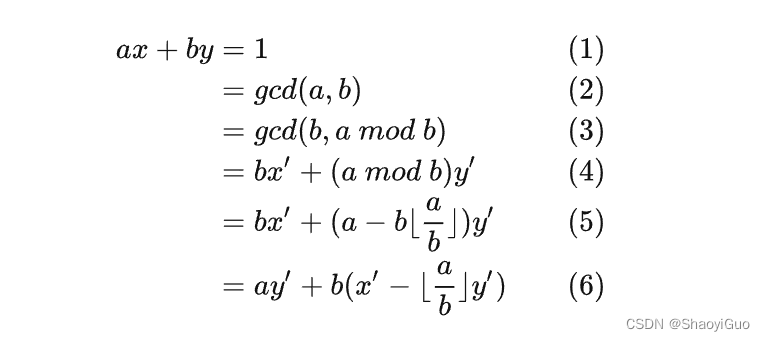
#include<iostream>
#include<cstring>
using namespace std;
int a, b;

int exgcd(int a, int b, int& x, int& y) {
	if (!b) {
		x = 1, y = 0;
		return a;
	}
	int d = exgcd(b, a % b, y, x);
	y -= a / b * x;
	return d;
}

int main() {
	cin >> a >> b;
	int x, y;
	exgcd(a, b, x, y);
	cout << (x % b + b ) % b << endl; //(x%b)表示x除以b的余数，即x对b取模的结果。然后，加上b的原因是为了避免负数的情况。最后，再次对b取模，确保结果在0到b-1之间
	return 0;
}

2、费马小定理 

 

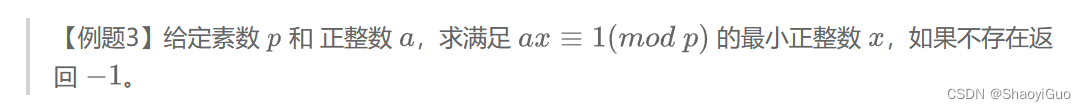
首先，当 a 为 p 的倍数时，ax ≡0(mod p)，所以一定不存在，直接返回 −1；否则，根据费马小定理，我们可以知道：

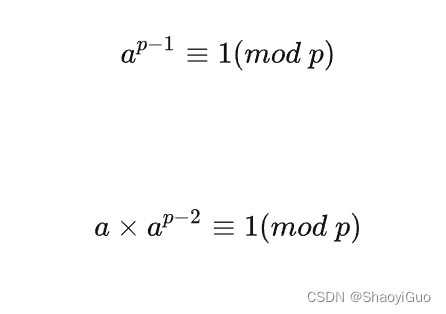
再对比原式可得：

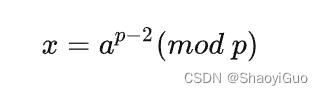
然后利用快速幂，即可求出x

 

#define ll long long
ll Exp(ll a,ll n, ll mod){
    ll ans = 1;
    while(n) {
        if(n & 1) 
            ans = ans * a % mod;
        a = a * a % mod;
        n >>= 1;
    }
    return ans;
}

ll Inv(ll a, ll p) {
    return Exp(a, p-2, p);
}