扩展欧几里得算法_逆元算法

逆元：

概念：

若ab≡1 (mod m),则称a与b在模m的情况下互为逆元。记b=a，所以b又叫a的数论倒数。

我们介绍两种方法求解逆元：

1.费马小定理：

假如p是质数，且gcd(a,p)=1，那么 a^(p-1)≡1(mod p)。即：假如a是整数，p是质数，且a,p互质(即两者只有一个公约数1)，那么a的(p-1)次方除以p的余数恒等于1。

逆元：对于a和p，若a*b%p≡1，则称b为a%p的逆元。

除法的逆元，即求(a/b)%p的值

通常情况下，p均为质数，则公约数为1的情况基本都可以保证

由费马小定理得：

b^(p-1)%p=1 则：

b*b^(p-2)%p=1 两边同乘a/b，然后左右式交换得：

a/b=a/b*b*b^(p-2)%p 化简得：

a/b=a*b^(p-2)%p

此时的结果即为a/b的结果，取模得(a/b)%p;

2.扩展欧几里得

为了介绍扩展欧几里得，我们先介绍一下贝祖定理：

即如果a、b是整数，那么一定存在整数x、y使得ax+by=gcd(a,b)。

换句话说，如果ax+by=m有解，那么m一定是gcd(a,b)的若干倍。(可以来判断一个这样的式子有没有解)

有一个直接的应用就是 如果ax+by=1有解，那么gcd(a,b)=1；

要求出这个最大公因数gcd(a,b)，我们最容易想到的就是古老悠久而又相当强大的辗转相除法：

int gcd(int a,int b){    return b==0?a:gcd(b,a%b);}

但是，对于上面的式子ax+by=m来说，我们并不仅仅想要知道有没有解，而是想要知道在有解的情况下这个解到底是多少。

所以，扩展欧几里得

        当到达递归边界的时候，b==0，a=gcd(a,b) 这时可以观察出来这个式子的一个解：a*1+b*0=gcd(a,b)，x=1,y=0，注意这时的a和b已经不是最开始的那个a和b了，所以我们如果想要求出解x和y，就要回到最开始的模样。

        初步想法：由于是递归的算法，如果我们知道了这一层和上一层的关系，一层一层推下去，就可以推到最开始的。类似数学上的数学归纳法。

        假设当前我们在求的时a和b的最大公约数，而我们已经求出了下一个状态：b和a%b的最大公因数，并且求出了一组x1和y1使得b*x1+(a%b)*y1=gcd

(注意在递归算法中，永远都是先得到下面一个状态的值)

这时我们可以试着去寻找这两个相邻状态的关系：

首先我们知道：a%b=a-(a/b)*b；带入：

b*x1 + (a-(a/b)*b)*y1

= b*x1 + a*y1 – (a/b)*b*y1

= a*y1 + b*(x1 – a/b*y1) = gcd   

发现 x = y1 , y = x1 – a/b*y1

这样我们就得到了每两个相邻状态的x和y的转化，就可以在求gcd的同时对x和y进行求值了

接下来我们重点用代码介绍扩展欧几里得求逆元。

首先引入快速幂与快速乘

ll qmul(ll a,ll b,ll m)                     //快速乘{  ll ans=0;  a%=m;  b%=m;  while(b)  {    if(b&1)    {      ans=(ans+a)%m;    }    a=(a+a)%m;    b>>=1;  }  return ans;}

ll fast_pow(ll x, ll k, ll p){                    //快速幂    ll ret=1;    x%=p;    while(k>0){        if(k&1){            ret= qmul(ret, x, p);        }        k>>=1;        x= qmul(x, x, p);    }    return ret;}

void extgcd(ll a,ll b,ll& d,ll& x,ll& y)            //拓展欧几里得{    if(!b)    {        d=a;        x=1;        y=0;    }    else    {        extgcd(b,a%b,d,y,x);        y-=x*(a/b);    }}ll ModularInverse(ll a,ll b){    ll d,x,y;    extgcd(a,b,d,x,y);    return d==1?(x+b)%b:-1;  //返回的结果就是(1/a)mod(b)的结果    // complete this part}

引入一道例题：蓝桥杯2019A组省赛E题

附解题代码：

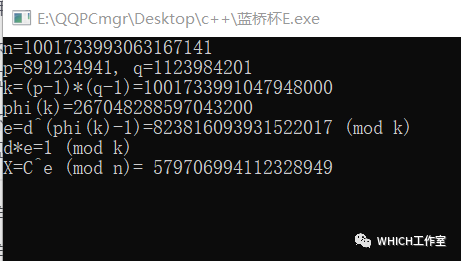
#includeusing namespace std;typedef long long ;qq fast_mul(qq x, qq y, qq p){    qq ret=0;    x%=p, y%=p;    while(y>0){        if(y&1){            ret= (ret+x)%p;        }        y>>=1;        x= (x+x)%p;    }    return ret;}qq fast_pow(qq x, qq k, qq p){    qq ret=1;    x%=p;    while(k>0){        if(k&1){            ret= fast_mul(ret, x, p);        }        k>>=1;        x= fast_mul(x, x, p);    }    return ret;}qq phi(qq n){    qq ret= n;    for(int i=2;i*i<=n;i++){        if(n%i==0){            ret= ret/i*(i-1);            while(n%i==0) n/=i;        }    }    if(n!=1){        ret= ret/n*(n-1);    }    return ret;}qq get_p(qq n){    for(qq i=2;i<=n;i++){        if(n%i==0){            return i;        }    }}int main(){    qq n = (qq)1001733993063167141;    qq d = 212353;    qq C = 20190324;    qq p,q,e,k;    printf("n=%lld\n",n);    p=get_p(n);    q=n/p;    printf("p=%lld, q=%lld\n",p,q);    k=(p-1)*(q-1);    printf("k=(p-1)*(q-1)=%lld\n",k);    printf("phi(k)=%lld\n",phi(k));    e=fast_pow(d,phi(k)-1,k);    printf("e=d^(phi(k)-1)=%lld (mod k)\n",e);    printf("d*e=%lld (mod k)\n",fast_mul(d,e,k));    qq X=fast_pow(C,e,n);    printf("X=C^e (mod n)= %lld\n",X);    while(1)getchar();    return 0;}

运行结果如下：