L5: Design, Properties, Examples, and Applications of Constraint Satisfaction Problems (CSP)

本文链接：https://blog.csdn.net/m0_74331272/article/details/146338991

English Summary: Design, Properties, Examples, and Applications of Constraint Satisfaction Problems (CSP)

1. Design of CSPs

Constraint Satisfaction Problems (CSPs) are structured problems that consist of:

A set of variables {X_1, X_2, ..., X_n\}.
A set of domains DiD_i for each variable, which define possible values.
A set of constraints {C_1, C_2, ..., C_m\}, specifying allowable value combinations.

Each constraint limits how variable values can be assigned to ensure valid solutions.

2. Properties of CSPs

Assignment: Assigning values to variables.
Consistent Assignment: Does not violate constraints.
Complete Assignment: All variables receive values.
Solution: A complete and consistent assignment.
Optimization: In some cases, an objective function is used to find the best solution.

3. Examples of CSPs

Map Coloring Problem:
- Each region of a map must be colored with one of three colors (Red, Green, or Blue).
- No two adjacent regions can have the same color.
- The problem can be represented using constraint graphs, where nodes are regions, and edges represent adjacency constraints.

4. Applications of CSPs

Graph Coloring: Used in scheduling, register allocation in compilers, and circuit design.
Sudoku and Puzzles: Formulated as CSPs where each cell must satisfy number constraints.
AI Planning: Used in robotics, route planning, and automated reasoning.
Resource Allocation: Assigning tasks, workforce, or assets under constraints.

中文翻译: 约束满足问题 (CSP) 的设计、性质、示例及应用

1. CSP的设计

约束满足问题（CSP）是结构化问题，由以下部分组成：

一组变量 {X_1, X_2, ..., X_n\}。
每个变量的取值范围（域） DiD_i 。
一组约束 {C_1, C_2, ..., C_m\}，规定变量之间允许的值组合。

约束限制了变量的值分配方式，以确保解的有效性。

2. CSP的性质

赋值：为变量分配值。
一致性赋值：不会违反任何约束。
完全赋值：所有变量均被赋值。
解：一个完整且一致的赋值方案。
优化：某些情况下，通过 目标函数 找到最优解。

3. CSP的示例

地图着色问题：
- 地图上的每个区域必须用三种颜色（红、绿、蓝）之一着色。
- 相邻区域不能使用相同的颜色。
- 问题可用约束图（constraint graph） 表示，节点代表区域，边表示相邻区域的限制关系。

4. CSP的应用

图着色问题：用于排课、编译器寄存器分配、电路设计等。
数独与拼图：要求满足一定规则的约束问题。
人工智能规划：用于机器人、路线规划和自动推理。
资源分配：用于任务调度、人员分配和资产管理。

通俗解释

CSP 就像一个填色游戏：

你有多个变量（比如国家、省份、数独的格子）。
你可以为它们选择不同的值（比如颜色、数字）。
但必须遵守一定规则（比如相邻区域不能有相同颜色）。
你的目标是找到所有变量的合适值，让整个系统满足规则。

想象你要安排考试时间表：

变量 = 课程
值 = 考试时间段
约束 = 不能安排相同时间给同一学生的不同考试

CSP 让问题变得有统一规则，所以计算机可以用通用算法解决不同类型的任务。

English Notes for Memorization

CSP Components:
- Variables {X_1, X_2, ..., X_n\}
- Domains {D_1, D_2, ..., D_n\}
- Constraints {C_1, C_2, ..., C_m\}
CSP Key Properties:
- Assignment: Giving values to variables.
- Consistency: No constraint is violated.
- Completeness: All variables are assigned.
- Solution: A complete & consistent assignment.
Example: Map Coloring:
- Nodes = Regions
- Edges = Adjacency constraints
- Colors = Red, Green, Blue (cannot be the same for neighbors)
CSP Applications:
- Graph Coloring (Scheduling, Circuit Design)
- Sudoku & Games (Puzzle Solving)
- AI Planning (Robotics, Route Optimization)
- Resource Allocation (Task Scheduling)

By remembering CSP as a coloring or scheduling problem, it becomes easier to understand its general structure and wide applications.

拆解设计者的思维过程：为什么是“变量、域、约束”？

1. 设计者的核心目标：把“现实问题”抽象成“可计算的数学结构”

想象你是一个计算机科学家，面对五花八门的问题（地图着色、排课、数独），你发现它们的共性：

需要填的“坑” → 变量（Variables）
比如地图上的国家、课程表的课程、数独的格子
每个“坑”能填的“土” → 值域（Domains）
比如颜色、时间、数字
填土时的“禁忌规则” → 约束（Constraints）
比如相邻国家颜色不同、同一学生课程时间不冲突、数独行/列不重复

设计者的灵感：把现实问题中的“可调节参数”抽象为变量，把“可选方案”抽象为值域，把“规则限制”抽象为约束。这样，计算机就能用统一的方法（如回溯算法）解决所有这类问题。

2. 为什么是这三个概念？——从具体问题到抽象框架

案例1：地图着色

实际需求：给澳大利亚7个州着色，相邻州颜色不同。
设计者的观察：
- 变量 = 7个州（必须填的“坑”）
- 值域 = 红、绿、蓝（每个州能选的“土”）
- 约束 = 相邻州颜色不同（填土时的“禁忌”）

案例2：数独

实际需求：填满9x9格子，满足行/列/宫格不重复。
抽象映射：
- 变量 = 81个格子（每个格子是一个待填的“坑”）
- 值域 = 数字1-9（每个格子的“土”）
- 约束 = 行、列、3x3宫格内数字不重复（填数字的“禁忌规则”）

设计者的顿悟：所有这类问题都能抽象为“填坑-选土-避禁忌”的模型，于是CSP的三大概念诞生。

3. 为什么不用其他概念？——抓住问题的“最小必要元素”

设计者需要一套最简框架，既能覆盖大多数问题，又不引入冗余。试想：

如果只有变量和值域（没有约束）：相当于随便填，没有规则，问题失去意义。
如果只有约束（没有变量和值域）：约束无从作用，问题无法具体化。

变量、值域、约束是描述这类问题的最小完备集：

变量定义“问题中有哪些可调节的开关”
值域定义“每个开关能拨到哪些档位”
约束定义“哪些档位组合是合法的”

就像电路设计中的“电源、开关、逻辑门”——缺一不可。

4. 设计者的深层动机：让计算机像人类一样“推理”

人类解决填色或排课时，会：

观察哪里最难填（比如被最多邻国包围的州） → 变量选择启发式
排除不可能选项（比如邻国用了红色，自己就不能选红） → 约束传播
试错并回溯（选错颜色后擦掉重填） → 回溯算法

设计者把人类的直觉思考翻译成数学语言：

变量选择启发式 → 优先选“剩余可选值最少的变量”（最受限变量优先）
约束传播 → 用弧相容（AC-3算法）提前排除矛盾
回溯 → 系统化地探索解空间

CSP的本质：把人类的问题解决逻辑，转化为计算机可执行的步骤。

5. 终极答案：设计者是为了“标准化复杂问题”

标准化变量：让问题中的“可调节因素”明确化
比如物流问题中的“货物运输路线”作为变量
标准化值域：明确每个因素的“可选方案”
比如运输路线可选“空运、陆运、海运”
标准化约束：用数学描述“现实世界的限制”
比如“易碎品不能陆运”“总成本不超过预算”

设计者的野心：用一套模型统一解决调度、优化、决策问题，让计算机成为“万能问题破解器”。这就是CSP的终极意义。

幻灯片 10：示例CSP——地图着色

节点(N)：代表变量（地图中的区域）。
弧(A)：代表约束（相邻关系）。
图表示：
- 使CSP在不同问题上具有通用性。
- 使用状态转移模型和目标测试。
- 可采用通用启发式进行求解。

要点：用给节点着色的方式逐步构建一个小型CSP问题。

幻灯片 11：CSP的增量表述

类似搜索树：
- 初始状态：空赋值 {}。
- 转移模型：
  - 选择一个未被赋值的变量。
  - 为其分配符合约束的值。
- 目标测试：当所有变量都被赋值时，得到完整解。
- 路径代价：每一步通常是固定代价。

要点：可视化为一个分支树，依次给变量赋值。

幻灯片 12：CSP的增量表述（DFS）

解的特征：
- 必须是完整赋值。
- 出现在搜索树的深度 n（n是变量数）。
- 仅需搜索到深度 n，深度优先搜索（DFS） 非常适合CSP。
路径并不重要：
- 我们只关心最终解，不在意搜索路径。
- 优化：可以加目标函数来选择最佳解。

要点：使用DFS构建搜索树，直到所有变量都完成赋值。

2. DFS的路径覆盖机制

深度优先搜索的增量表述要求逐层为变量赋值，每层对应一个变量的选择。例如，在数独问题中，每个空格的赋值对应搜索树的一层，81个空格对应深度81的搜索路径。

约束传播的局限性：尽管约束传播（如前向检验、弧相容）可以提前排除部分无效分支（如某变量值域为空时回溯），但这仅减少搜索宽度而非深度。DFS仍需按变量数n逐层展开，直到所有变量完成赋值或发现冲突。

3. 最坏情况下的深度必然性

虽然实际搜索中可能提前找到解（例如在深度k < n时已完成合法赋值），但以下两种场景仍要求搜索树深度为n：

唯一解位于最深层的场景：例如，某CSP的解要求最后一个变量的某个特定值才能满足约束，此时必须遍历到深度n。
无解场景的验证：若问题无解，DFS需遍历所有可能的完整赋值路径（深度n的叶子节点），才能最终确认无解

“增量表述”在CSP中的含义

一、通俗解释：一步步搭积木

想象你要用积木搭一座塔：

增量表述：每次只加一块积木，直到塔的高度达到目标层数。
- 每一步只处理一块积木（对应一个变量），且必须按顺序从底层到顶层逐步搭建。
- 必须搭满所有层数（n层），才算完成目标（完整解）。

CSP的增量表述：

每个变量的赋值就像放一块积木。
必须处理完所有变量（搭满n层）才能得到一个完整的解。
中途无法跳过任何步骤（无法提前完成）。

二、专业定义：逐步扩展部分解的搜索过程

在CSP的深度优先搜索（DFS）中，增量表述（Incremental Formulation） 指：

逐层构建解：每深入搜索树的一层，为一个变量赋值。
路径的完整性：解的路径必须覆盖所有n个变量（深度为n）。
回溯的机制：若当前赋值导致约束冲突，则回退到上一层（父节点），尝试其他可能的值。

核心特点：

逐步性：每次只处理一个变量，解是逐步构建的。
系统性：通过深度优先的顺序，穷举所有可能的赋值组合。

三、为什么必须到深度n？——解的结构要求

CSP的解必须满足完整性（所有变量均被赋值）。因此：

搜索树的每一层对应一个变量：
- 根节点（深度0）：未赋值任何变量。
- 叶子节点（深度n）：所有变量均被赋值，可能为合法解或冲突。
中途无法确认解的存在：
- 即使前k层（k < n）的赋值已满足所有约束，仍需继续为剩余n–k个变量赋值，才能验证是否全局一致。
- 反例：若中途停止（深度k < n），可能剩余变量因值域受限无法赋值，导致部分解无效。

案例：数独问题

即使前80个格子已正确填入数字，第81个格子可能因约束无值可选，此时需回溯调整之前的赋值。

四、增量表述 vs 非增量表述

对比维度	增量表述（CSP+DFS）	非增量表述（如BFS或状态空间搜索）
解的结构	逐变量赋值，路径长度为n	可能跳跃式赋值，路径长度不确定
搜索深度	严格等于变量数n	可能小于n（如通过合并状态提前找到解）
适用场景	必须完整赋值的约束问题	部分赋值即可验证解的问题（如路径规划）
典型算法	回溯算法（Backtracking）	A*算法、广度优先搜索（BFS）

五、增量表述的优化：约束传播与启发式

尽管必须遍历到深度n，但通过以下方法减少无效搜索：

前向检验（Forward Checking）：
- 每次赋值后，立即更新剩余变量的值域，提前排除冲突分支。
  例如：地图着色中，若为变量A赋值红色，相邻变量B的值域自动移除红色。
最受约束变量优先（MRV）：
- 优先处理值域最小的变量（最可能触发约束传播）。
最少约束值优先（LCV）：
- 为当前变量优先选择对剩余变量限制最少的值。

效果：

减少搜索树的宽度（剪枝无效分支），但深度仍为n。
例如：数独问题通过约束传播，实际搜索路径远小于理论最大值981。

六、总结：为什么“增量表述”是CSP的核心？

结构性：将问题分解为逐变量的决策步骤，符合人类逐步推理的习惯。
完备性：确保所有可能的解都被探索，避免遗漏。
可优化性：与约束传播、启发式策略无缝结合，提升搜索效率。

最终答案：
“增量表述”是CSP中一种逐层、逐步构建解的搜索方式，通过DFS确保所有变量被依次处理。尽管必须遍历到深度n，但通过约束剪枝和启发式策略，实际搜索效率远高于暴力枚举。这就像“必须填满所有空格，但用智能规则跳过死胡同”。

幻灯片 13：CSP的完全状态表述

完全赋值：
- 所有变量都有值（但不一定都满足约束）。
局部搜索：
- 适用于CSP，通过迭代改进解。
离散且有限的变量取值：
- 示例：地图着色、八皇后问题。

要点：展示了美国地图与八皇后问题，说明局部搜索可以在完整赋值的基础上迭代改进。

通俗与专业结合的“Complete State”解析

一、通俗比喻：填表格与交卷

想象你在填写一份考试卷：

Partial State（部分状态）：只填了选择题，填空题和大题还没写。
Complete State（完整状态）：所有题目都填了答案（不管对错）。
Solution（解）：所有题目都填了正确答案（既完整又正确）。

CSP中的Complete State：

所有变量都已被赋值（无论是否满足约束），就像交卷时必须填满所有题目。
只有同时满足所有约束的Complete State才是合法解，如同考试得满分。

二、专业定义：Complete State vs Solution

Complete State（完整状态）
- 定义：所有变量均被赋值（无论是否违反约束）。
- 特点：
  - 出现在搜索树的叶子节点（深度等于变量数n）。
  - 可能合法（满足所有约束），也可能非法（存在冲突）。
示例：
- 地图着色中，所有州都被赋予颜色（即使相邻州颜色相同）。
- 数独中，所有格子都填入数字（即使行/列/宫格重复）。
Solution（解）
- 定义：既是Complete State，又满足所有约束。
- 特点：
  - 合法性验证需在赋值完成后进行。
  - 只有部分Complete State是合法解。
示例：
- 地图着色中，所有相邻州颜色不同。
- 数独中，所有行、列、宫格数字不重复。

三、为什么Complete State必须深度为n？——搜索树的刚性规则

搜索树的逐层构建
- 每个层级对应一个变量的赋值。
- 根节点（深度0）：未赋值任何变量。
- 叶子节点（深度n）：所有变量均被赋值（Complete State）。
例如：在澳大利亚7州着色问题中，搜索树深度为7，每个叶子节点代表7个州均被着色（可能合法或非法）。
解的验证依赖Complete State
- 约束可能在赋值中途被违反（如地图着色中提前发现相邻州同色），但只有Complete State能验证全局合法性。
- 部分状态（Partial State）即使满足当前约束，也无法保证后续赋值不冲突。
反例：数独中前80格正确，但第81格可能无合法值，需回溯调整。

四、Complete State的应用场景

回溯算法（Backtracking）
- 深度优先搜索生成Complete State，验证后回溯剪枝。
- 例如：地图着色中尝试所有颜色组合，发现冲突则回溯。
约束优化问题（COP）
- 在Complete State基础上评估目标函数（如成本最小化）。
- 例如：物流调度中，所有货物分配路线后，计算总运输成本。
冲突分析与调试
- 通过非法Complete State定位冲突源头。
- 例如：芯片设计中发现信号干扰，需追溯具体布线错误。

五、总结：Complete State的本质

必要门槛：CSP的解必须通过Complete State的门槛，这是验证全局一致性的唯一方式。
效率平衡：尽管必须遍历到深度n，但通过约束传播和启发式策略，可以大幅减少无效Complete State的生成。

最终答案：
“Complete State”是CSP中所有变量均被赋值的状态（无论是否合法），它是验证解的必要条件。就像考试必须答完所有题才能评分，CSP必须生成Complete State才能判断是否满足约束。

为什么CSP图中提到“Local Search”？——完全状态下的高效探索

一、Local Search在CSP中的角色：从“完整但冲突”到“合法解”

在完全状态（Complete State）的CSP框架中，Local Search（局部搜索） 是一种通过逐步调整完整赋值来逼近合法解的策略。其核心思想是：

起点是一个完整但可能非法的赋值（例如所有州已着色但存在相邻同色）。
通过局部修改（如改变一个变量的值）逐步减少冲突数量，最终达到零冲突（合法解）。

图中的关键提示：

“Local search methods can work well here” → 完全状态CSP适合用局部搜索，因为无需维护部分解的一致性，直接操作完整状态。

二、Local Search的核心操作

定义邻域（Neighborhood）：
- 每个状态的邻域是所有通过单变量调整得到的新状态。
- 例如：地图着色中，修改一个州的颜色（从红→绿）生成一个邻域状态。
评估冲突（Objective Function）：
- 目标是最小化违反约束的数量（冲突数）。
- 例如：八皇后问题中，冲突数为互相攻击的皇后对数。
选择优化方向：
- 贪婪策略：选择冲突减少最多的调整。
- 随机扰动：避免陷入局部最优（如模拟退火）。

案例：

地图着色：若当前赋值有3对相邻州同色，调整某州的颜色可能减少到1对冲突。
八皇后：移动一个皇后到某列，使其与其他皇后不冲突。

三、为什么Local Search在完全状态CSP中高效？

避免系统性回溯：
- 传统回溯需逐层探索所有可能路径，复杂度指数级。
- Local Search直接操作完整状态，复杂度与冲突调整次数相关，适合大规模问题。
空间复杂度低：
- 只需维护当前状态和冲突信息，无需存储搜索树。
容忍暂时冲突：
- 允许暂时违反约束，通过逐步优化逼近合法解。

对比传统方法：

维度	回溯法（DFS）	Local Search
搜索方式	系统性遍历所有可能路径	随机或启发式调整当前状态
适用场景	小规模、精确解需求	大规模、快速近似解需求
冲突处理	遇到冲突立即回溯	允许暂时冲突，逐步优化

四、经典算法：最小冲突算法（Min-Conflicts）

步骤：
- 随机生成一个完整赋值（可能冲突）。
- 循环直到冲突数为0：
  1. 随机选择一个冲突变量（如相邻同色的州）。
  2. 将其值调整为当前值域中引发最少新冲突的值。
案例：
- 八皇后问题：平均仅需约50步调整即可找到合法解，远快于回溯法的8!=40320次尝试。
- 数独求解：通过调整冲突格子的数字，快速收敛到合法解。

五、Local Search的局限性

可能陷入局部最优：
- 若所有局部调整都无法减少冲突，需引入随机性（如随机重启）。
不保证找到解：
- 适用于存在较多解的问题（如地图着色），若问题无解则无法终止。

六、总结：图中为何强调Local Search？

完全状态的特性：允许从任意完整赋值出发，通过局部调整快速收敛。
CSP的离散有限域：变量值域明确，便于定义邻域操作。
大规模问题的实用性：对高维CSP（如百万变量调度问题），Local Search是唯一可行方法。

最终答案：
图中提到Local Search，是因为在完全状态的CSP中，它提供了一种高效启发式探索路径——从冲突的完整赋值出发，通过局部调整逼近合法解，尤其适合大规模或近似解需求的问题，如地图着色、八皇后、排课调度等。

幻灯片 14：CSP的复杂性

若最大域大小为 d:
- 所有可能赋值总数为 O(d^n)。
- 例如：地图着色若 d=3，则有 O(3^7)。
指数型增长：
- 随着变量数量增加，求解难度急剧上升。
效率：
- 虽然理论上是指数时间，但实际能通过启发式或搜索策略高效求解。

要点：强调CSP在理论上复杂度很高，但在实践中依然可行。

幻灯片 15：约束的类型

一元约束：
- 只涉及一个变量（如“SA ≠ 绿色”）。
- 可预处理以减少搜索空间。
二元约束：
- 涉及两个变量（如“SA ≠ NSW”）。
- 在约束模型中最常见。

要点：介绍不同约束形式对CSP求解的影响。

幻灯片 16：二元和高阶约束

二元CSP：
- 只包含二元约束。
- 可用约束图表示，图中的边代表变量之间的约束。
高阶约束：
- 涉及三个或以上变量。
- 无法用普通图表示，而需使用超图。
示例：文字算术谜题（如TWO + TWO = FOUR）。

要点：二元约束适合用简单图，三元及以上约束需更复杂的结构表示。

幻灯片 17：文字算术谜题的约束

变量必须两两不同：
- 常用的约束：Alldiff(F, T, U, W, R, O)。
- 或分解成多个二元约束（F≠T, T≠U, 等）。
数学约束：
- 字母对应的数字必须满足加法方程。

要点：通过字母加法展示了如何将高阶数学关系转化为CSP约束。

English Summary for Each Slide

Slide 10: Example CSP – Map Coloring

Nodes (N): Represent variables (regions on a map).
Arcs (A): Represent constraints (adjacency relations).
Graph Representation:
- Makes CSPs uniform across problems.
- Uses a transition model and goal test.
- General-purpose heuristics apply.

👉 Illustration: A small CSP problem is incrementally built by assigning colors to nodes.

Slide 11: Incremental Formulation of CSP

Similar to a search tree:
- Initial State: Empty assignment {}.
- Transition Model:
  - Select an unassigned variable.
  - Assign a value while ensuring constraints are met.
- Goal Test: Solution is complete when all variables have values.
- Path Cost: A constant cost per step.

👉 Illustration: A branching tree where variables are assigned in sequence.

Slide 12: Incremental Formulation of CSP (DFS)

Solution properties:
- Must be a complete assignment.
- Appears at depth n (n variables).
- Search extends only to depth n, making Depth-First Search (DFS) well-suited for CSP.
Path irrelevance:
- We care about the solution, not how we got there.
- Optimization: An objective function can be used to pick the best solution.

👉 Illustration: DFS tree representation for solving CSP problems.

Slide 13: Complete-state Formulation of CSP

Complete assignment:
- All variables are assigned values (not necessarily valid).
Local search:
- Works well for CSP, refining solutions iteratively.
Discrete & finite domains:
- Example: Map-coloring, 8-queens problem.

👉 Illustration: A US state map and an 8-queen problem grid.

Slide 14: Complexity of CSP

If max domain size dd:
- The number of possible assignments is O(dⁿ).
- Example: Map coloring where d=3d = 3 results in O(3⁷) complexity.
Exponential growth:
- As the number of variables increases, solving becomes harder.
Efficiency:
- Despite exponential complexity, CSP techniques solve problems efficiently.

👉 Illustration: A cartoon representing the overwhelming complexity of CSP.

Slide 15: Types of Constraints

Unary Constraints:
- Involve one variable (e.g., "SA ≠ green").
- Can be preprocessed to reduce complexity.
Binary Constraints:
- Involve two variables (e.g., "SA ≠ NSW").
- Common in constraint-based models.

👉 Illustration: Different types of constraints in CSP.

Slide 16: Binary & Higher-order Constraints

Binary CSP:
- Uses only binary constraints.
- Can be represented as a constraint graph.
Higher-order Constraints:
- Involve three or more variables.
- Cannot be represented as a normal graph, but as a hypergraph.
Example: Cryptarithmic puzzles (TWO + TWO = FOUR).

👉 Illustration: Graph representation and a cryptarithmic puzzle.

Slide 17: Cryptarithmic Puzzle Constraints

All variables must be different:
- Constraint: Alldiff(F, T, U, W, R, O)
- Alternative: Collection of binary constraints (F ≠ T, T ≠ U, etc.).
Mathematical Constraints:
- Digits must satisfy arithmetic equations.

👉 Illustration: Mathematical representation of letter-based addition puzzles.

Summary of CSP

Graph-based approach simplifies problem representation.
Incremental search models (DFS) help solve CSP.
Complexity grows exponentially but can be managed efficiently.
Constraints guide variable assignments and restrict invalid solutions.
Real-world applications: Scheduling, Sudoku, AI planning, resource allocation.

幻灯片 18：“CSP中的无启发式搜索与启发式搜索”

核心思路：对比了在约束满足问题（CSP）中使用两种搜索策略：
- 无启发式搜索（Uninformed Search）：没有特定启发式的系统化遍历。
- 启发式搜索（Informed Search）：利用问题的特定信息或通用启发式来提高搜索效率。
背景：该片介绍在CSP中如何用最简单的方式（无启发式）或更智能的方式（启发式）来进行搜索。

幻灯片 19：“CSP中的回溯搜索（Backtracking Search）”（上）

增量式CSP算法：像构造一棵搜索树一样，每次仅给一个变量赋值。
可交换赋值（Commutative Assignments）：先给WA=red然后NT=green，和先给NT=green再WA=red在最终结果上没差别。
深度优先搜索(DFS) + 单变量赋值就称为回溯搜索（Backtracking Search，BS）。
回溯搜索原因：它是CSP最基本的“无启发式”解法，逐个变量尝试赋值，如果无法继续，就回溯到上一步重新尝试。

为什么CSP中的赋值顺序不影响结果？——可交换赋值的本质

一、专业解释：约束的静态性与独立性

在约束满足问题（CSP）中，约束是变量之间的静态关系，而非依赖于赋值顺序的动态规则。
例如，在地图着色问题中，约束是“相邻区域颜色不同”，无论赋值顺序如何，最终结果只需满足这一条件。

WA=红和NT=绿的赋值顺序：
- 若先赋WA=红，则NT的可用值域自动排除红色。
- 若先赋NT=绿，则WA的可用值域自动排除绿色。
结果等价性：只要最终WA和NT的值不同，无论顺序如何，均满足约束。

数学本质：
CSP的约束是布尔逻辑表达式（如WA ≠ NT），其真值仅由变量的最终值决定，与赋值顺序无关。

二、通俗比喻：拼图与规则

想象你在拼一副拼图：

规则：相邻拼图块必须颜色匹配。
拼装顺序：无论先拼左上角还是右下角，只要最终所有相邻块颜色匹配即可。
可交换性：调整拼图块的顺序不影响最终成品的合法性。

CSP的类比：

拼图块 = 变量
颜色匹配规则 = 约束
拼装顺序 = 赋值顺序

三、设计者的底层逻辑：约束的全局性

CSP的设计者将问题抽象为静态的变量-约束网络，而非动态的状态转移过程：

变量独立性：每个变量的值仅受其直接约束的变量影响，而非历史路径。
约束的同步性：所有约束在赋值完成后统一验证，而非按顺序逐步生效。

案例对比：

非交换性场景（如状态空间搜索）：
机器人移动顺序（先左转再前进 vs 先前进再左转）会导致不同位置，路径依赖性强。
CSP的可交换性：
变量赋值的最终合法组合唯一，顺序不影响结果。

四、为什么其他算法中顺序可能重要？

在非CSP问题中（如规划问题或强化学习），动作的时序性会影响结果：

动态环境：动作执行后环境状态改变，后续动作基于新状态。
顺序敏感：例如“先加水再加热”与“先加热再加水”结果不同。

CSP的独特性：

无状态性：变量的赋值不改变问题本身的约束结构。
全局验证：所有约束仅在最终状态统一检查，而非按顺序触发。

五、总结：CSP中的“可交换性”从何而来？

约束的静态定义：所有规则预先确定，不随赋值过程改变。
最终一致性验证：合法解仅取决于最终赋值是否满足所有约束，而非中间路径。
设计哲学：CSP的目标是找到满足所有约束的静态解，而非描述动态过程。

最终答案：
CSP的赋值顺序不影响结果，因为约束是全局、静态的规则。无论先给WA还是NT赋值，只要最终它们的颜色不同，约束即被满足。这就像“填色游戏的规则只看最终颜色分布，不管你先涂哪块”。设计者通过这种抽象，将问题简化为纯粹的逻辑满足，而非过程依赖。

幻灯片 20：“CSP中的回溯搜索”（下）

通用方法可加速搜索，主要包括：
1. 决定下一个要赋值的变量。
2. 决定给该变量赋值的顺序。
3. 提早检测可能的失败。
4. 利用问题结构来减少搜索空间。
回溯搜索如果采用一成不变的顺序分配变量，也只是无启发式搜索。
启发式搜索在CSP中可能包括：
- 变量选择和取值顺序(如MRV、Degree等)
- 前向检查(Forward Checking)
- 基于冲突的改进方法(如Mini-Conflicts)

幻灯片 21：“变量选择顺序”（一）

关键决策：下一步该给哪个变量赋值？
示例：
- 如果 WA=red、NT=green已定，那么 SA 只剩一种可用颜色（blue），而 Q 还剩两种（red、blue）。
- 这时先给可用选项更少的 SA 赋值更好。
通用规则：选可行值最少的变量（又称“最少剩余值”启发式，MRV）。

幻灯片 22：“变量选择顺序”（二）

MRV（Minimum Remaining Value）启发式：
- 又称“最受限变量”。
- 每次优先选剩余可用值最少的变量。
Degree启发式：
- 如果是第一个要赋值的变量，就选与其他未赋值变量拥有最多约束关系的变量。
- 在澳大利亚地图中，SA 与 5 个邻居相连，所以它是度数最高的节点。

幻灯片 23：“变量选择顺序”（三）

Degree启发式的效果：
- 有时先选度数最高的变量能大幅减少回溯次数。
MRV vs. Degree：
- MRV整体更通用，但Degree在某些情况下也可作为辅助或首要选择。
选好变量之后：下一个问题是给它分配什么值。

幻灯片 24：“值的选择顺序”

Least Constraining Value（LCV）：
- 在选定要赋值的变量后，选择一个对其他未赋值变量约束最少的值。
- 即：赋值后尽量保留更多可选项给其他变量。
操作准则：
- 先选对邻接变量限制最少的值。
示例：
- Q可以是red或blue，若选red能让SA保留更多选择，就优先选red。

总体思路

以上内容说明在CSP中，最基础的“回溯搜索”可以通过一系列“启发式”增强来显著减少搜索成本，包括：

变量选择次序：MRV（最少剩余值）& Degree（最高度）
值选择次序：LCV（最少约束值）
前向检查或冲突检测等方法

这些技巧旨在减少搜索分支数并尽早发现冲突，从而加速约束满足问题的求解过程。

CSP中的搜索策略与启发式优化

(Search Strategies & Heuristic Optimization in CSP)

1. 无信息搜索 vs 启发式搜索 | Uninformed vs Informed Search

技术定义

无信息搜索 (Uninformed Search): 系统性地遍历解空间，不使用特定启发式规则。
例如：暴力回溯（Backtracking）尝试所有可能路径，直到找到解或穷尽所有选项。
启发式搜索 (Informed Search): 利用问题特定或通用启发式规则，高效引导搜索方向。
例如：优先处理“最受约束的变量”（MRV），减少无效分支。

通俗解释

无信息搜索：就像在迷宫中闭着眼睛摸墙走，遇到死胡同就原路返回。
启发式搜索：拿着迷宫地图和指南针，优先探索最可能通向出口的路径。

设计者初衷

目标：避免暴力搜索的指数级复杂度（如3n）。
灵感来源：人类解决复杂问题时的直觉（如填色时优先处理邻国最多的州）。

2. 回溯搜索（Backtracking Search）

技术定义

增量式算法 (Incremental CSP Algorithms): 逐层生成搜索树，每层仅为一个变量赋值。
例如：先为WA赋红色，再为NT赋绿色，依此类推。
交换性赋值 (Commutative Assignments): 变量赋值顺序不影响最终解。
例如：先WA=红后NT=绿，等价于先NT=绿后WA=红。
深度优先搜索 (DFS): 单变量赋值的DFS称为回溯搜索（Backtracking Search）。

通俗解释

回溯搜索：像搭积木一样逐块放置，如果发现当前块放错，就拆掉重试。
例如：数独中填入数字，若冲突则擦掉并尝试下一个数字。

设计者初衷

核心需求：避免存储所有中间状态，节省内存。
权衡取舍：牺牲部分时间效率（回溯次数多），换取空间效率（仅需维护当前路径）。

3. 启发式优化：变量排序 | Heuristic Optimization: Variable Ordering

技术定义

最少剩余值（MRV）启发式: 选择剩余可选值最少的变量（最受约束变量）。
例如：若SA只剩一种颜色可选，优先处理它。
度启发式（Degree Heuristic）: 选择与最多未赋值变量存在约束的变量。
例如：澳大利亚地图中，SA邻接5个州，优先处理。

通俗解释

MRV：先填数独中最难填的格子（只剩1个数字可选）。
度启发式：先解决影响范围最大的问题（如交通枢纽的调度）。

设计者初衷

减少分支因子（Branching Factor）：优先处理约束强的变量，降低后续选择复杂度。
早期剪枝（Early Pruning）：通过快速触发冲突，提前回溯（如SA无合法颜色时立即停止）。

4. 启发式优化：值排序 | Heuristic Optimization: Value Ordering

技术定义

最少约束值（Least Constraining Value）: 为变量选择对剩余变量限制最少的值。
例如：若Q选红色仅影响1个邻州，而选蓝色影响3个邻州，则优先选红色。

通俗解释

最少约束值：填色时选一种颜色，尽量不影响邻居的选择空间。
例如：给Q选红色，让SA还能选绿或蓝；若选蓝色，SA可能只剩红色（导致冲突）。

设计者初衷

保留灵活性：避免过早限制其他变量的选项，减少死胡同概率。
启发式目标：最大化解的潜在可能性，而非仅满足当前约束。

5. 完全状态公式与局部搜索 | Complete-state Formulation & Local Search

技术定义

完全赋值（Complete Assignment）: 所有变量均被赋值（可能非法）。
例如：地图着色中所有州已填色，但存在相邻同色。
局部搜索（Local Search）: 通过微调完全赋值逐步减少冲突。
例如：最小冲突算法（Min-Conflicts）调整冲突变量的值。

通俗解释

完全状态：先随便填满所有答案（即使有错误），再慢慢修正。
例如：数独先随机填满所有格子，再调整冲突数字。
局部搜索：像校对文章，逐处修正错误直到无错。

设计者初衷

应对大规模问题：传统回溯无法处理高维CSP（如百万变量调度），而局部搜索复杂度与冲突数相关。
容忍暂时错误：允许中间状态存在冲突，以空间换时间。

6. 设计者蓝图：CSP算法的演进 | Designer’s Blueprint

初始挑战：暴力回溯的指数爆炸问题（如3n复杂度）。
关键突破：将人类直觉转化为数学启发式（如MRV、度启发式）。
技术融合：
- 约束传播（Constraint Propagation）: 前向检验（Forward Checking）、弧相容（AC-3）。
- 启发式引导（Heuristic Guidance）: 变量与值排序策略。
扩展性优化：局部搜索（如Min-Conflicts）应对超大规模CSP。

通俗总结

CSP算法设计：像制定交通规则——先定义变量（路口）、值域（通行方向）、约束（红绿灯），再通过智能调度（启发式）避免拥堵。
核心哲学：用规则（约束）引导混乱（搜索空间），让计算机像人类一样“聪明地试错”。

中英对照结语

技术视角: CSP algorithms transform chaotic search spaces into structured logic through variables, domains, and constraints.
人文视角: 约束满足问题，是计算机对人类理性思维的数学致敬——用规则驯服无序，以逻辑抵达答案。

幻灯片 25：Forward Checking (FC) 的基本概念

执行时机：一旦变量 XXX 被赋值，就对所有与 XXX 之间存在约束的变量 YYY 更新其可行域（Domain）。
原理：从 YYY 的取值域中删除与 XXX 当前赋值不兼容的值，从而减少后续搜索空间。
示例：在澳大利亚地图着色中，当 WA=red 后，和 WA 相邻的变量（如 NT、SA 等）的域会去除 red；若之后 Q=green，再相邻的域会继续删除 green 等。

要点：Forward Checking 有效缩减了合法值的候选列表，使后续决策更明确。

幻灯片 26：Forward Checking (FC) 的关键点

核心思路：随时记录未赋值变量的剩余合法取值，一旦有变量出现“无合法值”时，立刻终止并回溯。
关键点 1：
- 例如当 WA=red、Q=green 时，NT 与 SA 的域可能只剩下一个可用值（blue）。
- 传播（propagating）信息能有效减少分支因子（如从 3 降到 1）。
- 结合 MRV(最少剩余值)，会自动提示下一个要赋值的变量。
效果：不断缩小搜索树规模，加速求解。

幻灯片 27：Forward Checking (FC) 的关键点（续）

关键点 2：
- 如果特定赋值导致某个变量的可行域变为空，就说明该组合不可能满足所有约束。
- 算法在检测到此不一致后会立即回溯，避免在“无解路径”上浪费时间。
示例：
- WA=red, Q=green, V=blue 可能让 SA 无法取值；FC 很快检测到 Dom(SA)={} 并回溯。

幻灯片 28：FC在约束传播中的局限性

问题：Forward Checking 并不能检测到所有类型的不一致。
- 例如，如果 NT 和 SA 同时被迫只能选择同一个值（blue），但它们又彼此相邻，这就冲突了。
解决思路：需要更进一步的约束传播(constraint propagation)，不仅要对变量进行域修剪，还要继续检查变量之间的约束本身是否冲突。

结论：仅通过 FC，仍可能漏掉某些更深层次的冲突，需要更强的传播算法（如“弧一致性”等）。

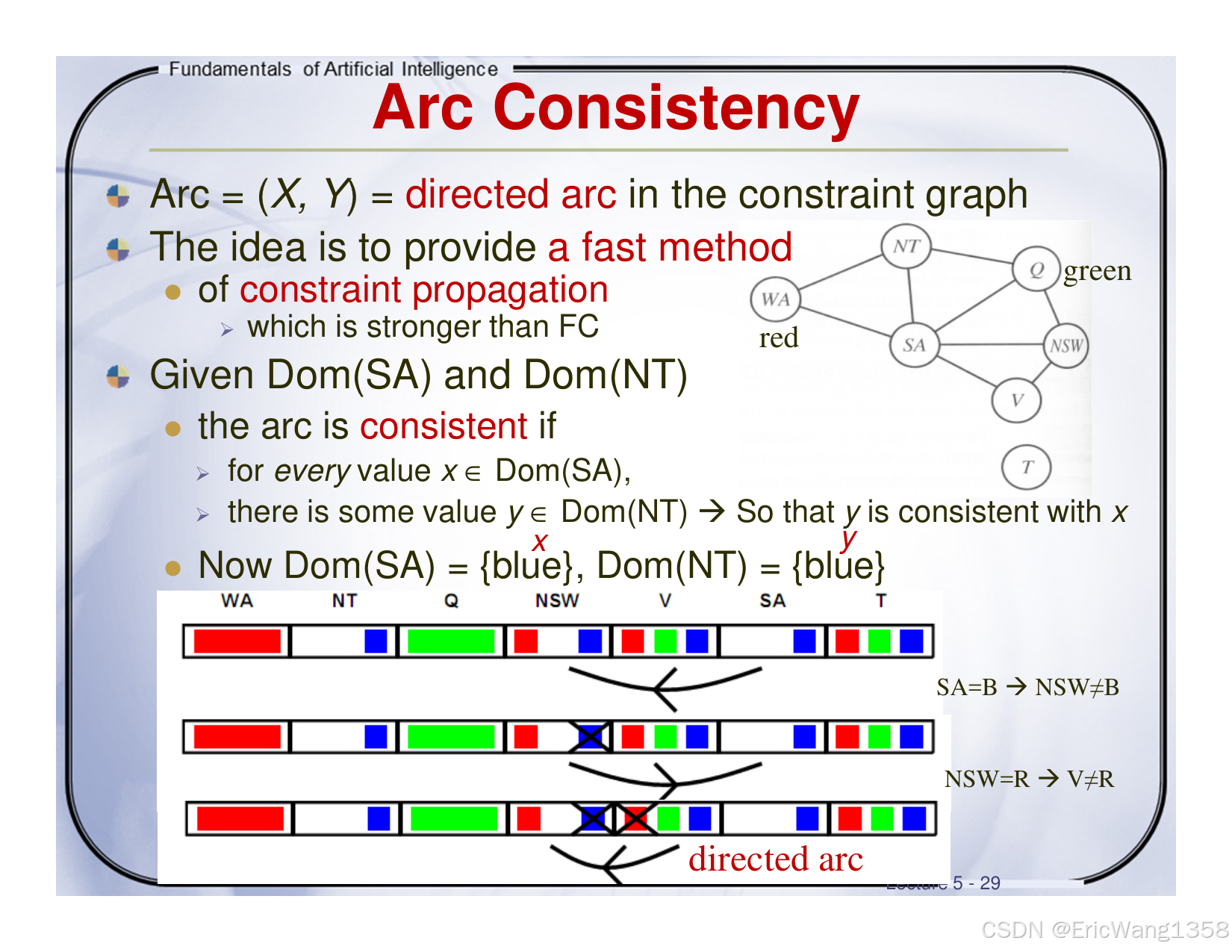
幻灯片 29：Arc Consistency（弧一致性）

概念：在约束图中，把一条弧视为有向边(X,Y)。我们希望对每个 x∈Dom(X)，都能在 Dom(Y)中找到至少一个 y 与之兼容。
作用：比 FC 更强的一种约束传播方法，可在搜索前或搜索过程中减少大量不必要的取值。
示例：若 SA 与 NT 都只有 {blue}，需判断这对邻居是否能共存（若约束是“不相同”，那就冲突了）。

幻灯片 30：Arc Consistency（弧一致性）续

流程：若某个变量失去一个可行值，则所有与它相邻的弧都要重新检查（反复更新）。
优势：相比 FC，弧一致性能更早发现失败或冲突，提高求解效率。
应用方式：
1. 预处理：在正式搜索前先做一遍弧一致性，把搜索空间先缩减。
2. 动态传播：每次赋值后都做局部更新。
终止条件：重复进行，直到没有新的不一致出现为止。

幻灯片 31：处理特殊约束（Handling Special Constraints）

场景：如果一个约束里有 m 个变量，但只有 n 个不同可用值，且 m>n，显然无法满足“所有不同”之类的高阶约束。
示例：
- 如果 {WA = red, NSW = red}，然后有约束 Alldiff(WA, SA, NT) 和 Alldiff(NSW, Q, SA)；剩下的 3 个变量却只剩 2 种颜色，就一定冲突。
要点：对于这类高阶约束，可以直接进行更多的解析或特殊判断（如Alldiff），而不必仅依赖二元局部检查。

约束传播的进阶：前向检验、弧一致性与高阶约束

1. 前向检验（Forward Checking, FC）的局限性

问题：FC仅修剪直接相邻变量的值域，无法检测跨变量的深层冲突。
示例：

赋值步骤：
1. 给WA赋红色 → 相邻的NT、SA不能为红色。
2. 接着给NT赋绿色 → 相邻的SA不能为绿色。
3. 此时SA的值域可能被修剪为仅剩蓝色。
潜在冲突：
- 若SA的邻国Q也被修剪到仅蓝色，而SA和Q相邻，则两者只能选蓝色 → 冲突未被FC检测。

根本原因：
FC仅更新当前变量的邻域，未传播到更远变量。
设计者初衷：牺牲全面性换取效率，适用于简单问题。

2. 弧一致性（Arc Consistency, AC）的升级

定义：对每一条有向弧（X→Y），X的每个值x必须在Y的值域中存在至少一个y，满足X和Y的约束。
示例：

SA和NT的约束：颜色不同。
若SA的值域为{蓝}，NT的值域为{蓝} → 无合法y满足SA≠NT → 弧不一致。

流程：

预处理：搜索前对所有弧执行AC，缩小值域。
动态传播：每次赋值后，重新检查相关弧的一致性。

优势：

更早发现冲突：例如SA和NT同时只剩蓝色时，立即报错。
减少搜索空间：修剪更多无效值，加速回溯。

对比FC：

维度	前向检验（FC）	弧一致性（AC）
传播范围	仅直接相邻变量	所有相关弧的变量对
检测能力	遗漏跨变量冲突	检测多级传播的冲突
计算开销	低	高（需多次迭代检查）

3. 处理高阶约束（如Alldiff）

场景：当变量数超过可用值数量时，必然冲突。
示例：

约束：Alldiff(WA, SA, NT)（三者颜色不同）。
可用颜色：红、绿 → 仅2种，但需3个不同值 → 无解。

解决方法：

值域分析：若变量数m > 可用值数n，直接判定无解。
特殊约束传播：
- 超弧一致性（Hyper-AC）：针对多变量约束（如Alldiff）设计的高级传播。
- 全局约束解析：例如识别Alldiff中的“m > n”情况，提前终止搜索。

设计哲学：

普通AC的局限：仅处理二元约束，无法应对多变量逻辑。
高阶约束优化：将全局逻辑转化为剪枝规则，避免无谓搜索。

4. 总结：约束传播的层次化策略

基础层（FC）：快速但粗粒度，适合简单问题。
进阶层（AC）：全面但耗时，应对复杂约束。
高阶层（全局约束）：专用逻辑处理，解决特殊场景。

实战建议：

小规模问题：优先使用AC预处理。
大规模问题：结合FC和动态AC，平衡效率与效果。
特殊约束：直接编码全局规则（如Alldiff的m ≤ n检查）。

最终答案：
前向检验（FC）因局部修剪而遗漏跨变量冲突，弧一致性（AC）通过多级传播提前拦截矛盾，而高阶约束需全局逻辑分析。设计者通过层次化策略，逐步逼近问题本质，以智能剪枝取代暴力搜索。

幻灯片 33：Local Search for CSP

局部搜索在CSP中的效果：
- 常常能很好地解决很多CSP问题。
- 使用完全状态表述：初始状态中所有变量都有一个赋值（不管是否满足约束）。
- 状态转移模型：通过一次只改变一个变量的值来“移动”到下一个状态。
- 例如：8皇后问题就是典型的CSP。
核心问题：在局部搜索中，如果要重新给某个变量赋值，应当怎样选这个值？
- 最常见的启发式是 min-conflicts（最小冲突策略）。
- 意思：选使与其他变量冲突数最少的那个值。

幻灯片 34：Local Search for CSP——Min-Conflicts 启发式

基本原理：
- 在当前状态中，针对任意一个出现冲突（违规）的变量，尝试为它重新选择一个值。
- 这个新值应当能最小化它与其它变量之间的冲突数。
示例：
- 以4皇后问题为例，每个状态是4列皇后的位置组合，共有 44=2564^4 = 25644=256 种。
- 目标测试：没有皇后互相攻击。
- 代价函数 h(n)：冲突（攻击）数。

幻灯片 35：Min-Conflicts Heuristic（伪代码与示例）

Min-Conflicts算法框架：
1. 从一个完整赋值开始（可能有冲突）。
2. 若当前赋值已满足所有约束，则返回这个解。
3. 否则，从有冲突的变量中随机挑一个。
4. 选择一个令冲突数最小的值赋给该变量。
5. 重复以上过程，直到找到解或到达最大迭代步数。
示例：
- 棋盘中每一列放一个皇后，通过不断修改相冲突列中的皇后行位置，直到冲突数减到0。

幻灯片 36：Local Search for CSP

Min-Conflicts的运行时间：
- 经验上“与问题规模无关”或仅弱相关。
- 即使是百万级的皇后问题，也能在平均约50步内找到解（实验结果）。
局部搜索的另一个优势：
- 在“动态环境（dynamic environment）”下依旧效果良好。
- 回溯搜索（Backtracking）在环境变化时往往效率低下，需要大量时间和内存。
- 而局部搜索能快速在当前完整赋值的基础上小步迭代，适应环境变化。

总结：Min-Conflicts 的核心思想

从一个初始完整状态开始，每次只修改有冲突的变量使其冲突最小化，并进行迭代。
对大规模CSP非常有效，尤其适用于8皇后或更大规模的皇后问题，也能灵活应对环境动态变化。

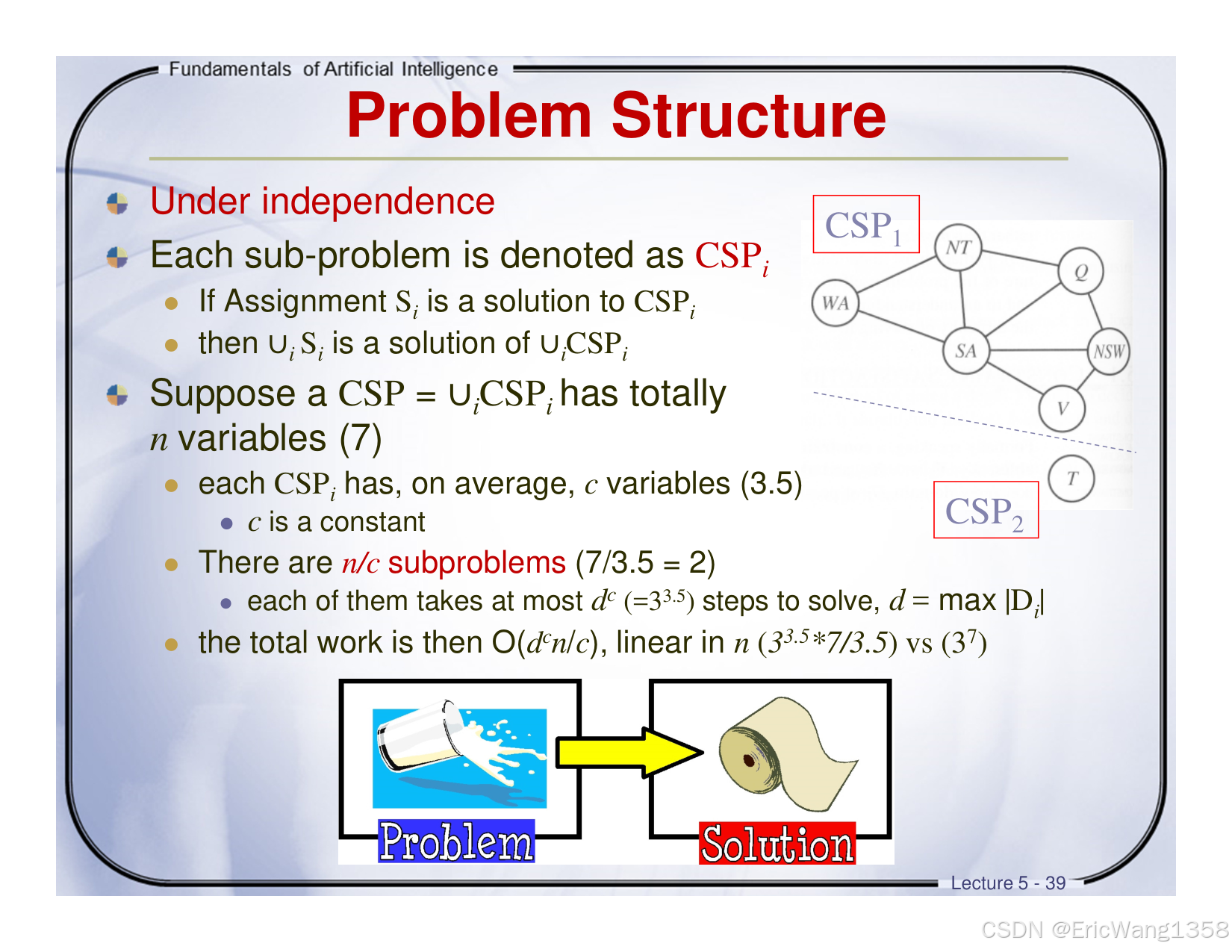
幻灯片 38：Problem Structure（从澳大利亚地图示例看“独立性”）

问题结构有助于快速求解：
- 如果大问题可分解成相互独立的子问题，分别求解后再合并。
“Divide and Conquer”思想：
- 把实际大问题切分成子问题，单独处理，再组合结果。
示例：澳大利亚地图
- 区域 T（塔斯马尼亚）与其他地区没有交互约束，相当于一个独立的子问题。
- 原本是 O(d^n) 的复杂度，但把 T 单独分出去后，就变成两部分，各自的规模更小，搜索复杂度大幅下降。
独立性识别：
- 可以从约束图中观察哪些节点（变量）与其他部分没有直接或传递性关联。

幻灯片 40：最简单情况：树形结构的CSP

树形CSP：
- 若约束图是一棵树，则任意两变量之间最多只有一条路径。
- 这种CSP可在线性时间（随变量数呈线性增长）内求解。
解决思路：
1. 选任意变量作为根（root）。
2. 从根到叶子按顺序进行“回退”检查（backward removal），验证并修剪不满足约束的取值。
结果：树状CSP极易求解，因为无环结构，减少了大量重复检查。

幻灯片 41：把一般图转换为树形的思路（Reducing Graph into Tree）

背景：我们有处理树形CSP的高效算法，但实际CSP通常图中有环，不是树。
问题：如何将带环的约束图转化为树形，使得已有算法可以应用？
两种方法：
1. Removing nodes（删除节点）：可能意味着用“节点一致化”等技巧来简化图。
2. Combining nodes（合并节点）：将某些相关节点打包成一个“超级节点”，从而减少环、形成树形结构。
意义：通过这两类操作，我们可将一般的CSP图转化为“接近树”或“树分解”形式，以便在该结构上用线性算法处理。

幻灯片 42：Removing Nodes（移除节点）

思路：先为某些变量临时分配取值，以便剩余未赋值的变量在约束图中形成一棵“树”结构。
示例：在澳大利亚地图中，如果先把 SA 固定为 red，并同步删除不兼容取值（如邻接区域不能再选 red），剩余的变量（WA, NT, Q, NSW, V, T）就构成一个树型图。
- 这时，就可以使用高效的树形CSP求解算法去处理剩余变量。
注意：对 SA 的赋值只是一种试探，若最终发现冲突，需要回溯并尝试其它取值。

幻灯片 43：Combining Nodes（合并节点）

构造Tree Decomposition（树分解）：
- 将原始约束图转化为一组“相互连通的子问题”。
- 每个子问题各自求解，然后将它们的解组合起来。
举例：
- 澳大利亚地图的着色问题可以分解成 5 个互相关联的子问题，每个子问题只包含部分区域的变量及对应约束。

幻灯片 44：Tree Decomposition 的基本条件

A tree decomposition必须满足：
1. 每个变量在原问题中都至少出现在某个子问题里，不会丢失任何变量。
2. 如果两个变量在原问题中有约束（相邻关系），那么它们必须一起出现在至少一个子问题中（包含它们及该约束）。
3. 如果某个变量出现在多个子问题里，则该变量必须出现在连接这些子问题路径上的每个子问题中，以保持一致性。
示例：
- 在澳大利亚地图上，如 Q 与 SA 有约束，那么在树分解中至少有一个节点包含这二者。

幻灯片 45：Combining Nodes（合并节点）的细节

“Mega-variable”（超级变量）：
- 在树分解中，每个节点包含一组原变量，例如 {WA, SA, NT}。
- 这个超级变量的取值域就是这些原变量的所有可能联合赋值，部分组合可能满足约束，部分则不满足。
应用方式：
- 把树分解中的每个节点视作一个超级变量，然后用“树形CSP算法”来为这些超级变量选取合适的“集合赋值”。
最终结果：
- 当所有超级变量的取值都和相邻节点保持一致，就得到原问题的整体解。

为什么树形CSP可以在线性时间内求解？

1. 树形结构的核心优势：无环约束传播

树形CSP的约束图是一棵无向无环图（即树），任意两个变量之间只有一条唯一路径。这种结构消除了环路导致的重复约束冲突，使得约束传播可以单向进行，无需回溯或重复检查。

示例：
假设一个树形CSP有5个变量（A→B→C→D→E），约束为相邻变量值不同：

根节点A赋值后，B的值域自动修剪（排除A的值）。
B赋值后，C的值域修剪，依此类推。
无环路 → 每个变量的值域修剪仅受父节点影响，不会循环依赖其他分支。

2. 线性时间求解的关键步骤

树形CSP的求解算法（如拓扑排序 + 前向检验）分为两步：

拓扑排序：从根节点到叶子节点确定处理顺序（如A→B→C→D→E）。
前向修剪：按顺序依次为每个变量赋值，并修剪子节点的值域。

时间复杂度分析：

拓扑排序：O(n)，通过一次深度优先遍历实现。
前向修剪：每个变量与其父节点和子节点交互，每次操作为O(1)。
总时间：O(n) + O(n) = O(n)（线性复杂度）。

3. 对比普通图结构CSP的指数级复杂度

普通图结构的CSP可能存在环路（如A→B→C→A），导致：

约束传播循环：A的值影响B，B影响C，C又影响A，需多次迭代才能稳定。
回溯爆炸：可能需遍历指数级数量的路径（如O(d^n)，d为值域大小）。

树形CSP的降维打击：
无环结构将指数级复杂度降为线性，因每一步仅需处理父节点的单一约束。

4. 为何“感觉错误解需要O(n)时间”是误解？

用户可能的混淆点在于：

错误解的判定：在树形CSP中，若某变量无合法值（值域为空），算法会立即终止，无需遍历所有变量。
实际流程：
1. 若父节点A赋值为红，子节点B的值域自动排除红色。
2. 若B的值域为空 → 直接判定无解，总时间为O(1)（实际远小于n）。
3. 仅当所有变量均有合法值时才需完整遍历，时间为O(n)。

结论：无论是否有解，树形CSP的最坏时间复杂度仍为O(n)。

5. 实战案例：树形地图着色

假设一个树形区域（国家A→省B→市C→区D），颜色值域为{红, 绿}，约束为相邻区域颜色不同：

赋值顺序：A→B→C→D。
操作步骤：
- A=红 → B值域为{绿} → B=绿 → C值域为{红} → C=红 → D值域为{绿} → D=绿。
结果：合法解，耗时4步（线性于变量数）。

若值域为{红}（仅一种颜色）：

A=红 → B值域为空 → 立即终止，无需处理后续变量，耗时1步。

总结

树形CSP的线性时间复杂度源于其无环结构和单向约束传播特性：

无环路：避免重复检查和回溯。
拓扑排序：确保每个变量仅依赖父节点，无需全局协调。
即时终止：一旦发现冲突立即终止，无需遍历所有变量。

最终答案：
树形CSP的线性时间求解是因其无环结构允许约束单向传播，通过拓扑排序和前向修剪，每一步仅处理一个变量且无需回溯，总步骤数与变量数成严格线性关系。即使存在错误解，算法也能在O(n)时间内完成判定。

逐页中文概括与通俗解析

幻灯片 42：移除节点（Removing Nodes）

核心思想：

先固定部分变量，让剩余的约束图变成一棵树，从而利用树形CSP的高效算法。
通俗比喻：
- 假设你在拼一幅复杂的拼图，暂时固定其中一块（比如拼图角落），剩下的部分更容易按顺序拼接，避免来回调整。

操作步骤（以澳大利亚地图着色为例）：

固定关键变量：比如先给SA（南澳）赋值红色。
修剪邻域值域：SA的邻接区域（WA、NT、Q等）不能再选红色。
剩余结构成树：此时WA、NT、Q等剩余的约束关系变成树形（无环）。
快速求解剩余：用树形CSP算法（线性时间）完成其他区域着色。

注意事项：

固定SA的赋值可能是试探性的，若后续发现冲突（如邻国无法着色），需回溯并尝试其他颜色。

设计者思路：

将复杂图问题转化为树形问题，牺牲部分试探成本，换取整体效率提升。

幻灯片 43：合并节点（Combining Nodes）

核心思想：

将多个变量合并为“超级变量”，构造树形分解（Tree Decomposition），分而治之。
通俗比喻：
- 把拼图分成几个小模块，先拼好每个模块内部，再按模块之间的接口组合成整体。

操作步骤：

划分子问题：将原问题分解为多个子问题，每个子问题包含一组变量及其约束。
例如：将澳大利亚分解为{WA, SA, NT}、{SA, Q}、{Q, NSW}等子问题。
构建树结构：子问题之间形成树形连接，避免环路。
独立求解子问题：每个子问题单独求解（如确定WA、SA、NT的合法颜色组合）。
组合全局解：根据子问题之间的接口约束，合并各子问题的解。

设计者思路：

通过分治策略，将复杂问题拆解为简单子问题，降低全局求解复杂度。

幻灯片 44：树分解（Tree Decomposition）的条件

三大条件：

覆盖性：原问题的每个变量必须出现在至少一个子问题中。
例如：澳大利亚的每个州必须属于某个子问题。
约束完整性：原问题的每条约束必须包含在某个子问题中。
例如：若SA和Q相邻，则必须有一个子问题同时包含SA和Q。
路径一致性：若一个变量出现在多个子问题中，这些子问题必须在树分解的路径上连续出现。
例如：若SA出现在子问题A和B中，则A和B之间的路径上的所有子问题都必须包含SA。

通俗解释：