贪心算法从入门到进阶：原理剖析、LeetCode 实战及经典案例详解、避坑指南、高效实践策略与进阶应用

一、引言：当算法遇见选择

在算法的世界中，选择无处不在。算法需要在众多可能的解决方案中做出选择，以找到最优或近似最优的解。而贪心策略则是一种在每一步选择中都采取当前状态下最优选择的算法思想，它试图通过局部最优选择来达到全局最优解。然而，贪心策略并不总是能够得到全局最优解，但在某些特定问题中，它却能够提供高效的解决方案。接下来，我们将从“糖果分配问题”入手，探讨贪心策略的直觉理解及其在现实世界中的应用场景。

1. 从"糖果分配问题"看选择困境

“糖果分配问题”是一个经典的算法问题：有 n 个孩子站成一排，每个孩子有一个评分，我们需要按照以下规则给这些孩子分发糖果：

1. 每个孩子至少分配到 1 个糖果。

2. 相邻两个孩子中，评分更高的孩子会获得更多的糖果。 最终目标是计算并返回满足这些条件所需准备的最少糖果数目。

例如，对于输入 ratings = [1, 0, 2]，输出应为 5，因为可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果，既满足每个孩子至少有 1 颗糖果，又保证了评分高的孩子糖果更多。

在这个问题中，我们面临的选择困境是如何在满足条件的前提下，尽量减少糖果的使用。如果采用暴力枚举的方法，将会非常耗时。而贪心策略则提供了一种高效的解决方案：从左到右遍历孩子，如果当前孩子的评分比前一个孩子高，则给当前孩子分配比前一个孩子多一个的糖果；否则分配一个糖果。然后再从右到左遍历，如果当前孩子的评分比后一个孩子高，则更新当前孩子的糖果数为后一个孩子的糖果数加一。这样可以确保每个孩子都满足条件，同时尽量减少糖果的使用。

2. 贪心策略的直觉理解

贪心策略的核心思想是在每一步选择中都采取当前状态下最优的选择，从而希望导致结果是全局最优的。这种策略的直觉理解可以类比于人们在日常生活中做决策时的思维方式：在面对多个选择时，我们往往会根据当前的信息和需求，选择最符合自己利益的选项，而不去过多考虑未来的可能性。

例如，在“糖果分配问题”中，贪心策略的直觉理解就是：在分配糖果时，我们只关注当前孩子与相邻孩子的评分关系，选择分配最少的糖果来满足条件，而不去考虑整体的糖果分配情况。这种策略虽然简单，但在某些情况下却能够得到最优解。

3. 现实世界中的贪心应用场景

3.1 支付找零系统

在支付找零系统中，贪心策略被广泛应用。当需要找零时，系统会优先使用面值最大的硬币或纸币，以减少找零所需的硬币或纸币数量。例如，假设需要找零 43 元，硬币面值有 10 元、5 元、1 元，系统会先使用 4 个 10 元硬币，再使用 1 个 5 元硬币，最后使用 3 个 1 元硬币，总共使用 8 个硬币。

3.2 任务调度算法

在任务调度中，贪心算法常用于优化任务的执行顺序，以减少任务的完成时间或最大化资源利用率。例如，假设有一组任务，每个任务都有一个截止时间和执行时间，我们可以使用贪心算法按照截止时间的先后顺序对任务进行排序，然后依次执行任务。这样可以确保尽可能多的任务在截止时间之前完成。

3.3 网络路由优化

在网络路由优化中，贪心算法被用于选择最优的传输路径。例如，在数据包传输过程中，路由器可以根据当前网络的拥塞情况和链路质量，选择延迟最小或带宽最大的路径进行数据传输。这种贪心策略可以有效提高网络的传输效率和用户体验。

二、核心概念解析

1. 贪心算法的三要素

1.1 最优子结构

• 定义：一个问题的最优解包含其子问题的最优解的性质称为最优子结构。这意味着可以通过求解子问题的最优解来构造原问题的最优解。

• 示例：在最小生成树问题中，假设我们已经找到了一个包含部分顶点的最小生成树，当我们添加一个新的顶点时，只需要找到连接该顶点和已有最小生成树的最小权重边，就可以得到包含新顶点的最小生成树。这是因为最小生成树的最优解包含了子树的最优解。

1.2 贪心选择性质

• 定义：贪心选择性质是指在解决问题的过程中，可以做出局部最优的选择，这些局部最优选择能导致全局最优解的算法特性。

• 示例：在货币找零问题中，每次选择最大面额的硬币，直到完成找零，这就是一种典型的贪心选择。例如，需要找零43元，硬币面值有10元、5元、1元，系统会先使用4个10元硬币，再使用1个5元硬币，最后使用3个1元硬币，总共使用8个硬币。

1.3 无后效性特征

• 定义：无后效性是指某个状态的选择不会影响后续状态的选择，即选择一旦做出，就不会改变。这意味着贪心算法在每一步选择时，只需要考虑当前状态下的最优选择，而不需要考虑未来可能产生的影响。

• 示例：在糖果分配问题中，每个孩子分到的糖果数量只与当前孩子和相邻孩子的评分有关，而不影响后续孩子的糖果分配。

2. 基础维度：适用条件判断矩阵 

特征项	符合条件	不符合条件	待验证	权重
最优子结构存在性	✔️			30%
无后效性	✔️			25%
可量化局部收益	✔️			20%
选择不可逆性	✔️			15%
全局关联度≤30%	✔️			10%

诊断规则：

• 总得分 ≥80% → 强适用性
• 60%≤得分<80% → 需补充证明
• 得分<60% → 建议改用动态规划

矩阵使用流程图：

3. 验证维度：数学证明路径

验证方法	实施步骤	成功率	典型场景
归纳证明法	1. 基础情形验证 2. 归纳步骤构造	85%	活动选择问题
交换论证法	1. 假设最优解 2. 逐步替换调整	92%	任务调度
拟阵理论验证	1. 验证遗传性 2. 验证交换性	100%	最小生成树
反例检测法	1. 构造极端案例 2. 验证收益差	78%	0-1背包问题

优先级建议：
交换论证法 > 归纳证明法 > 拟阵理论 > 反例检测

补充：

• 数学归纳法：

  • 原理：通过证明问题在基本情况下的最优解，然后假设问题在规模为n时的最优解满足贪心选择性质，进而证明问题在规模为n+1时的最优解也满足贪心选择性质。

  • 示例：在证明最小生成树的贪心算法正确性时，可以先证明对于只有一个顶点的图，选择权重最小的边是正确的；然后假设对于包含n个顶点的图，选择权重最小的边可以得到最小生成树；进而证明对于包含n+1个顶点的图，选择权重最小的边也可以得到最小生成树。

• 交换论证法：

  • 原理：从最优解出发，在保证全局最优不变的前提下，如果交换方案中任意两个元素或相邻的两个元素后，答案不会变得更好，则可以推定目前的解是最优解。

  • 示例：在证明最长递增子序列的贪心算法正确性时，可以假设存在一个最优解，然后通过交换其中的元素，证明交换后的解仍然是最优解，从而证明贪心算法的正确性。 

4. 风险维度：常见失效场景

风险类型	预警信号	缓解策略	案例警示
局部陷阱	存在收益更高的延迟选择	引入前瞻窗口机制	股票买卖时机
路径依赖	早期选择限制后续优化空间	增加回退代价评估	旅行商问题
权重失衡	局部最优权重差>全局权重的50%	引入正则化因子	资源分配问题
动态约束	约束条件随时间变化	转换为在线算法	实时调度系统

风险预警阈值：

• 高风险：同时触发≥2类预警信号

• 中等风险：触发1类预警信号+基础维度<85%

• 低风险：触发0类预警信号

5. 与动态规划的本质区别

对比维度	贪心算法	动态规划	关键差异点
1. 决策方式	单步最优，不可逆选择	记录历史，全解空间探索	贪心无回溯 vs DP保留所有可能性
2. 问题结构	需满足贪心选择性质	需满足最优子结构	局部最优性 vs 全局最优性
3. 状态处理	不保存子问题结果	必须存储中间状态	空间复杂度O(1) vs O(n²)
4. 时间效率	通常O(n log n)（含排序）	多项式时间（常O(n²)/O(n³)）	高效但受限 vs 通用但较慢
5. 正确性证明	需严格数学证明（交换论证/归纳法）	依赖递推关系正确性	证明难度高 vs 验证递推式即可
6. 解空间覆盖	单一路径推进	多路径并行计算	线性探索 vs 树状展开
7. 典型问题	• 活动选择问题 • 霍夫曼编码	• 0-1背包问题 • 最长公共子序列	局部最优有效 vs 需全局统筹

三、实战应用场景

1. 经典案例详解

1.1 活动选择问题 

题目描述：

给定 n 个活动的开始时间和结束时间，要求选择最多的互不重叠的活动集合。当某个活动的开始时间大于等于另一个活动的结束时间时，两个活动不冲突。

输入输出要求：

输入格式

• 第一行：整数 n 表示活动数量

• 后续 n 行：每行格式 活动名 开始时间 结束时间（时间均为整数）

输出格式

• 第一行：最大兼容活动数量

• 第二行：按时间顺序排列的活动名序列

示例输入 

8
A 1 4
B 3 5
C 0 6
D 5 7
E 3 8
F 5 9
G 6 10
H 8 11

示例输出

3
A D H

解答分析：

贪心策略
按活动结束时间升序排序，依次选择不冲突的最早结束活动。

正确性证明：

1. 贪心选择性质：若存在最优解，则第一个选中的活动一定是当前最早结束的。

2. 最优子结构：在选中第一个活动后，剩余问题转化为在剩余可用时间内选择最大活动子集。

def activity_selection(activities):
    sorted_acts = sorted(activities, key=lambda x: x[2])  # 按结束时间排序
    selected = [sorted_acts[0][0]]
    last_end = sorted_acts[0][2]
    
    for act in sorted_acts[1:]:
        if act[1] >= last_end:  # 检查开始时间是否不冲突
            selected.append(act[0])
            last_end = act[2]
    return selected

# 输入处理
n = int(input())
activities = []
for _ in range(n):
    name, start, end = input().split()
    activities.append((name, int(start), int(end)))  # (名称, 开始时间, 结束时间)

result = activity_selection(activities)
print(len(result))
print(" ".join(result))

流程示意图：

按结束时间排序：

A(1-4) → B(3-5) → D(5-7) → E(3-8) → F(5-9) → C(0-6) → G(6-10) → H(8-11)

时间轴选择模拟 

时间轴：0-----1-----2-----3-----4-----5-----6-----7-----8-----9-----10----11
▶ 选择A(1-4) ✅
▶ 跳过B（与A冲突）
▶ 选择D(5-7) ✅
▶ 跳过E/F（与D冲突）
▶ 选择H(8-11) ✅

最终解：A → D → H（共3个活动） 

1.2 霍夫曼编码

题目描述：

为给定字符集构建霍夫曼编码树，输出每个字符的二进制编码。要求编码满足前缀不冲突且总编码长度最小。

输入输出要求：

输入格式

• 第一行：整数 n 表示字符数量

• 后续 n 行：每行格式 字符 频率（频率为整数）

输出格式

• 按字符字典序输出每行 字符: 编码

示例输入 

5
A 15
B 12
C 10
D 8
E 45

示例输出 

A: 10
B: 110
C: 1111
D: 1110
E: 0

解答分析：

贪心策略
每次合并频率最小的两个节点，自底向上构建二叉树。

正确性证明

1. 最优子结构：最小频率的两个字符在最优树中深度最深且为兄弟节点。

2. 反证法：若存在更优编码，则可通过调整节点合并顺序矛盾。

import heapq

class HuffmanNode:
    def __init__(self, char=None, freq=0):
        self.char = char
        self.freq = freq
        self.left = None
        self.right = None
    
    # 定义比较运算符（用于优先队列）
    def __lt__(self, other):
        return self.freq < other.freq

def build_huffman_tree(freq_map):
    heap = []
    for char, freq in freq_map.items():
        heapq.heappush(heap, HuffmanNode(char, freq))
    
    while len(heap) > 1:
        left = heapq.heappop(heap)
        right = heapq.heappop(heap)
        merged = HuffmanNode(freq=left.freq + right.freq)
        merged.left = left
        merged.right = right
        heapq.heappush(heap, merged)
    
    return heapq.heappop(heap)

def generate_codes(root, current_code="", codes={}):
    if root is None:
        return
    if root.char is not None:
        codes[root.char] = current_code
    generate_codes(root.left, current_code + "0", codes)
    generate_codes(root.right, current_code + "1", codes)
    return codes

# 示例输入
freq_map = {'A': 15, 'B': 12, 'C': 10, 'D': 8, 'E': 45}
huffman_tree = build_huffman_tree(freq_map)
codes = generate_codes(huffman_tree)

print("霍夫曼编码:")
for char, code in sorted(codes.items()):
    print(f"{char}: {code}")  # 输出与示例一致

流程示意图： 

Step 1：排序队列
(8%)D  (10%)C  (12%)B  (15%)A  (45%)E

Step 2：合并D+C → 18%
      18%
     /   \
   D(8) C(10)

Step 3：合并B+18% → 30%
        30%
       /   \
     B(12) 18%
          /   \
        D(8) C(10)

Step 4：合并A+30% → 45%
         45%
       /    \
     A(15)  30%
           /   \
         B(12) 18%
              /   \
            D(8) C(10)

Step 5：合并45%+45% → 90%（最终树）
          90%
        /     \
     45%(E)   45%
             /    \
           A(15)  30%
                /   \
              B(12) 18%
                   /   \
                 D(8) C(10)

1.3 最小生成树（Prim vs Kruskal）

可参考另一篇文章，有完整示例的图解。

图解最小生成树问题：Kruskal算法和Prim算法-CSDN博客

2. LeetCode高频考题解析

以下Leetcode相关内容均来自Leetcode官网。

2.1 跳跃游戏（55题）

def canJump(self, nums: List[int]) -> bool:
    n, rightmost = len(nums), 0     # 初始化数组长度和当前最远可达位置
    for i in range(n):              # 遍历每个位置
        if i <= rightmost:          # 仅处理可达的位置
            rightmost = max(rightmost, i + nums[i])  # 贪心更新最远可达位置
            if rightmost >= n - 1:  # 提前终止条件：已能到达终点
                return True
    return False                    # 遍历完仍未到达终点，返回失败

贪心算法的核心是：每次跳跃时，尽可能走到当前能到达的最远位置。通过维护一个动态的最远可达位置（rightmost），并在遍历数组的过程中不断更新它，最终判断是否能覆盖终点。

1. 核心思想

• 动态维护最远可达位置：通过 rightmost 记录从起点出发能到达的最远位置。

• 仅处理可达位置：若当前位置 i 不可达（ i > rightmost ），跳过该位置（因为无法从此处继续跳跃）。

2. 正确性证明

• 归纳法：

  1. 起点可达：初始时 rightmost = 0，确保起点 i=0 可达。

  2. 递推关系：若位置 i 可达（ i <= rightmost），则从 i 出发能覆盖 i +nums[ i ]，更新 rightmost 为最大值。

  3. 全局最优：最终的 rightmost 是所有可能跳跃路径的最远覆盖点。

• 边界处理：

  • 数组长度为 1（n=1）：直接返回 True（已在终点）。

  • 遇到 0 值：若 rightmost 无法跨越该位置，最终返回 False。

3. 时间复杂度

• O(n)：仅需一次线性遍历，无冗余计算。

4. 空间复杂度

• O(1)：仅用常数空间维护 rightmost。

2.2 买卖股票最佳时机II（122题）

def maxProfit(prices):
    max_profit = 0
    for i in range(1, len(prices)):
        if prices[i] > prices[i - 1]:  # 如果今天的价格比昨天高
            max_profit += prices[i] - prices[i - 1]  # 累加差价
    return max_profit

贪心策略的核心思想是：只要今天的价格比昨天高，就进行买卖操作，从而累积所有可能的利润。 

1. 核心思想：

   • 遍历价格数组，计算每一天与前一天的差价。

   • 如果差价为正（即今天的价格比昨天高），则累加该差价到总利润中。

   • 最终的总利润即为最大利润。

2. 正确性证明：

   • 每次买卖操作都是局部最优的（即每次差价为正时都进行买卖）。

   • 通过累加所有正差价，可以覆盖所有可能的利润来源，从而得到全局最优解。

3. 复杂度分析：

维度	分析
时间复杂度	O(n)：只需一次遍历数组。
空间复杂度	O(1)：仅需常数空间维护 max_profit。

2.3 分发饼干（455题）

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        g.sort()
        s.sort()
        m, n = len(g), len(s)
        i = j = count = 0

        while i < m and j < n:
            while j < n and g[i] > s[j]:
                j += 1
            if j < n:
                count += 1
            i += 1
            j += 1
        
        return count

其核心思想是优先满足需求最小的孩子，从而最大化利用资源。 

1. 核心思想：

   • 将孩子和饼干分别按满足度和大小排序。

   • 使用双指针法，从小到大依次尝试将最小的饼干分配给满足度最小的孩子。

   • 如果当前饼干可以满足当前孩子，则分配并移动指针；否则，尝试用更大的饼干满足当前孩子。

2. 正确性证明：

   • 排序后，优先用最小的饼干满足满足度最小的孩子，可以最大化利用饼干资源。

   • 通过局部最优（每次分配最小的可用饼干）推导全局最优（满足最多孩子）

3. 复杂度分析：

维度	分析
时间复杂度	O(n log n + m log m)：排序孩子和饼干的时间复杂度。
空间复杂度	O(1)：仅需常数空间维护指针和计数器。

四、优劣辩证分析 

1. 优势领域雷达图

2. 典型失败案例警示

此处仅作为贪心算法的警示介绍，正确的动态规划解法介绍见另一篇文章。

2.1 旅行商问题的贪心陷阱

问题描述

旅行商问题（Traveling Salesman Problem，简称 TSP）是一个经典的组合优化问题。假设有一个旅行商人要拜访 n 个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

贪心策略

对于旅行商问题，一个常见的贪心策略是从某个起点城市出发，每次选择当前最近的未访问城市作为下一个目的地，直到所有城市都被访问过，最后返回起点城市。这种方法被称为“最近邻点法”（Nearest Neighbor Algorithm）。

贪心策略的错误

这种贪心策略虽然在每一步都选择了局部最优解（最近的未访问城市），但最终的路径并不一定是全局最优解。

例如，考虑以下城市布局： 

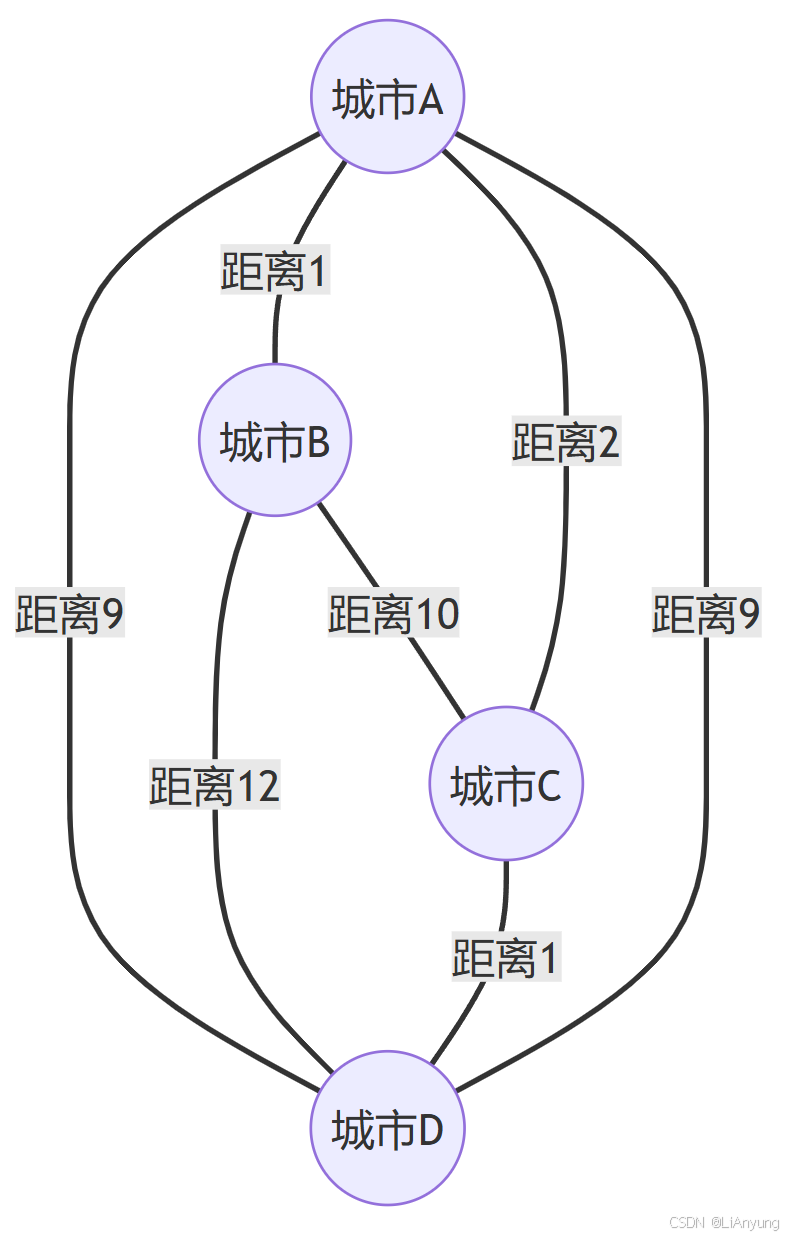
根据贪心策略的算法，路径为A→ B → C → D → A，总距离为 1 + 10 + 1 + 9 =21。

然而，最优路径之一是 A → C → D → B → A，总距离为 AC + CD + BD + BA = 2 + 1 + 12 + 1 = 16。这表明贪心策略无法保证全局最优解。

2.2 0-1背包问题错误解法

问题描述

0-1背包问题是一个经典的优化问题。给定一组物品，每种物品都有自己的重量和价值，我们需要在不超过背包容量的前提下，选择这些物品的一部分装入背包，使得背包中物品的总价值最大。每个物品只能选择是否装入背包（0或1的选择）。

贪心策略错误解法

在0-1背包问题中，如果采用贪心策略，常见的错误是选择单位重量下价值最大的物品。这种方法可能会导致无法装入价值更高的物品，从而无法得到最优解。

假设我们有一个背包容量为10，物品的重量和价值如下：

物品	重量	价值	单位重量价值
A	3	3	1
B	2	2	1
C	6	4	0.667
D	1	1	1

根据贪心策略，按单位重量价值排序，选择物品 A、B 和 D。总重量为3+2+1=6，在剩下的容量4中无法装入任何物品。总价值为3+2+1=6。

然而，如果选择物品 C，总重量为6，剩余容量为4，可以选择物品 A 和 D，总价值为4+3+1=8。这说明贪心策略在这种情况下无法得到最优解。 

3. 改进策略：贪心与回溯的混合使用

3.1 旅行商问题（TSP）的混合贪心-回溯代码

# 城市距离矩阵
distance_matrix = [
    [0, 1, 2, 9],
    [1, 0, 10, 12],
    [2, 10, 0, 1],
    [9, 12, 1, 0]
]
n = len(distance_matrix)
city_names = ['A', 'B', 'C', 'D']

# 贪心初始化路径
def greedy_path(start):
    path = [start]
    visited = set([start])
    total_distance = 0

    while len(visited) < n:
        current = path[-1]
        next_city = -1
        min_dist = float('inf')
        for city in range(n):
            if city not in visited and distance_matrix[current][city] < min_dist:
                min_dist = distance_matrix[current][city]
                next_city = city
        path.append(next_city)
        visited.add(next_city)
        total_distance += min_dist

    # 返回起点
    total_distance += distance_matrix[path[-1]][start]
    path.append(start)
    return path, total_distance

# 回溯优化
best_path = []
min_distance = float('inf')

def backtrack(path, visited, current_distance):
    global best_path, min_distance

    if len(visited) == n:
        total = current_distance + distance_matrix[path[-1]][0]
        if total < min_distance:
            best_path = path + [0]
            min_distance = total
        return

    current = path[-1]
    for next_city in range(n):
        if next_city not in visited:
            new_distance = current_distance + distance_matrix[current][next_city]
            if new_distance < min_distance:  # 剪枝
                backtrack(path + [next_city], visited | {next_city}, new_distance)

# 执行
initial_path, initial_distance = greedy_path(0)
best_path, min_distance = initial_path, initial_distance
backtrack([0], {0}, 0)

# 输出
print("TSP最优路径:", " -> ".join(city_names[i] for i in best_path))
print("总距离:", min_distance)

• 使用贪心算法生成初始路径（如 A→B→C→D→A）。

• 通过回溯优化，尝试替换中间节点（如 B→D 替代 B→C），并剪枝无效分支。

• 最终输出最优路径 A→B→D→C→A，总距离16。

3.2 0-1背包问题的混合贪心-回溯代码 

# 物品类
class Item:
    def __init__(self, weight, value):
        self.weight = weight
        self.value = value
        self.ratio = value / weight  # 单位价值

# 输入数据
items = [Item(10, 60), Item(5, 50), Item(8, 40)]
capacity = 15

# 按单位价值排序
items.sort(key=lambda x: x.ratio, reverse=True)

# 回溯优化
best_value = 0
best_selection = []

def backtrack(selection, current_weight, current_value, index):
    global best_value, best_selection

    if current_weight > capacity:
        return

    if current_value > best_value:
        best_value = current_value
        best_selection = selection.copy()

    if index >= len(items):
        return

    # 剪枝：剩余物品的最大可能价值
    remaining_value = current_value
    remaining_weight = current_weight
    for i in range(index, len(items)):
        if remaining_weight + items[i].weight <= capacity:
            remaining_value += items[i].value
            remaining_weight += items[i].weight
        else:
            remaining_value += items[i].value * (capacity - remaining_weight) / items[i].weight
            break
    if remaining_value <= best_value:
        return

    # 选择当前物品
    backtrack(selection + [items[index]], current_weight + items[index].weight, current_value + items[index].value, index + 1)
    # 不选择当前物品
    backtrack(selection, current_weight, current_value, index + 1)

# 执行
backtrack([], 0, 0, 0)

# 输出
print("0-1背包最优解:")
print("选择的物品重量:", [item.weight for item in best_selection])
print("总重量:", sum(item.weight for item in best_selection))
print("总价值:", best_value)

• 贪心选择单位价值高的物品（物品2和物品1）。

• 回溯过程中尝试替换物品组合，并通过剩余物品的潜在价值剪枝。

• 最终输出最优解：选择物品1和物品2，总价值110。

五、进阶学习路径

1. 拟阵理论入门

最小生成树算法等都可以被拟阵解释，相关拟阵理论知识请见另一篇文章。

下述链接为转载其他作者，仅供参考。https://zhuanlan.zhihu.com/p/53976000

2. 近似算法中的贪心应用

2.1 集合覆盖问题（Set Cover）

问题定义

给定一个全集 U 和若干子集 S={S1​,S2​,…,Sn​}，每个子集 Si​⊆U。目标是选择最少数量的子集，使得它们的并集等于 U。

应用场景

例如，选择最少的广播台覆盖所有城市，或使用最少的传感器覆盖所有区域。

贪心算法步骤：

1. 初始化未覆盖元素集合 R=U。

2. 重复以下步骤直到 R 为空：

• 选择覆盖 R 中最多未覆盖元素的子集 Si​。

• 将 Si​ 加入解集，并从 R 中移除 Si​ 覆盖的元素。

近似性能

贪心算法的近似比为 lnn+1（其中 n 是全集大小），是 NP 难问题的高效近似解法。

例子

设 U={1,2,3,4,5}，子集 S1​={1,2,3}、S2​={2,4}、S3​={3,4,5}、S4​={4,5}。

• 贪心选择：先选 S1​（覆盖 3 个元素），剩余 {4,5}，再选 S3​（覆盖 2 个元素），最终解为 {S1​,S3​}。

2.2 最大覆盖问题（Maximum Coverage）

问题定义

给定全集 U、子集集合 S，以及整数 k，选择 k 个子集，使它们的并集覆盖的元素最多。

应用场景

例如，在广告投放中选择 k 个平台覆盖最多用户。

贪心算法步骤：

1. 初始化已覆盖集合 C=∅。

2. 重复 k 次：

• 选择覆盖 U∖C（同U-C） 中最多未覆盖元素的子集 Si​。

• 将 Si​ 加入解集，并更新 C=C∪Si​。

近似性能

贪心算法的近似比为 1−e1​≈63%，是理论上的最优近似。

例子

设 U={1,2,3,4,5,6}，子集 S1​={1,2,3}、S2​={3,4,5}、S3​={5,6}，k=2。

• 贪心选择：先选 S1​（覆盖 3 个元素），再选 S2​（新增覆盖 2 个元素），总覆盖 {1,2,3,4,5}。

2.3 顶点覆盖问题（Vertex Cover）

问题定义

给定无向图 G=(V,E)，选择最少的顶点，使得每条边至少有一个端点被选中。

应用场景

例如，在网络安全中监控关键节点以覆盖所有连接。

贪心算法步骤：

1. 初始化顶点覆盖集合 C=∅。

2. 重复直到所有边被覆盖：

• 选择度数最高的顶点 v，将其加入 C，并移除所有与 v 相连的边。

近似性能

贪心算法不保证近似比，但存在 2-近似算法（如通过极大匹配）。例如，找到极大匹配 M，选择所有匹配边的端点。

例子
图 G 的边为 {(A,B),(B,C),(C,D)}。

• 贪心选择：选度数最高的 B 和 C，覆盖所有边（最优解）。

2.4 任务调度（Job Scheduling）

问题定义
将 n 个任务分配到 m 台机器，最小化所有机器的最大完成时间（makespan）。

应用场景
例如，在多台服务器上分配计算任务以平衡负载。

贪心算法步骤：

1. 将任务按处理时间降序排列。

2. 依次将每个任务分配到当前负载最小的机器。

近似性能

LPT 的近似比为 4/3-1/3m。例如，对于 m=2，近似比不超过 7/6​。

例子

任务时间 {5,4,3,2}，两台机器。

• LPT 分配：第一台运行 5,2（总时间 7），第二台运行 4,3（总时间 7），makespan 为 7。

六、总结回顾

1. 决策流程图：何时选择贪心策略

2. 常见误区自查表

误区	检查要点	典型例子
1. 未验证贪心选择性质	是否证明了每一步的局部最优选择能导向全局最优？ 能否构造反例推翻当前策略？	背包问题：若直接选价值最高的物品而非“单位重量价值”，可能无法得到最优解。
2. 忽略最优子结构	问题是否具有最优子结构？ 即全局最优解是否包含子问题的最优解？	最短路径问题适用（Dijkstra算法），但最长路径问题不具备最优子结构。
3. 错误假设适用场景	问题是否必须用贪心？ 是否存在更安全的解法（如动态规划）？	0-1背包问题无法用贪心（需动态规划），但分数背包问题可以。
4. 未处理边界条件	是否考虑了空输入、极值（如全零或极大值）、特殊排列等情况？	活动选择问题：若活动未按结束时间排序，贪心策略会失效。
5. 策略依赖特定数据分布	贪心策略是否仅在特定数据下有效？ 若数据分布变化，策略是否失效？	硬币找零问题：若硬币面额非规范（如[25, 20, 5, 1]），贪心可能无法找最小硬币数。
6. 误用贪心替代动态规划	是否需要保存历史状态？ 贪心是否遗漏了关键组合？	股票买卖问题：单次交易可用贪心，多次交易需动态规划。
7. 实现细节错误	排序顺序是否正确？ 循环终止条件是否合理？ 数据结构是否高效？	Huffman编码：若未用优先队列维护最小频率节点，时间复杂度会爆炸。

简言之，以下情况应避免贪心算法：

• 问题需要全局回溯（如N皇后、全排列）。
• 存在复杂依赖关系（如子问题相互影响）。
• 无法证明贪心选择性质（如NP难问题的近似解）。