Z曲线和Hilbert曲线的算法学习小结及代码实现

1．Z曲线

Z曲线编码方式相对简单，只要给出点的坐标（x，y）便可以立即给出其对于的Z映射值。

具体方法：

①读入x和y坐标的二进制表示；

②隔行扫描二进制位到一个字符串；

③计算出结果二进制串的十进制值。

图一

具体代码：

值得注意的是，采用Z映射的二维表的方阵行列数必须满足2的幂值，如1、2、4、8、16、32等等。

上述代码中加入了对输入坐标正确性及规范性的检验，输入坐标不合理将返回False。在平常运行时没有必要。（只是一时兴起）

2. Hilbert映射原理

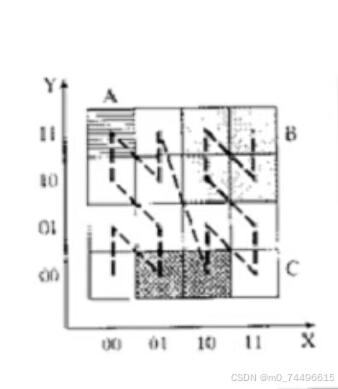
观察图一（a）Z映射，左下角起始块z=0，发现z=7的第八块（11，10）并未与临近块（11，01）相连，反而与对角块（00，01）相连，这导致其聚类性较差。

而Hilbert映射正是在Z映射基础上，将个别块进行位置调换，使连接性更好，聚类性更好。如下图所示。

图二

同样，Hilbert映射的二维表的方阵行列数必须满足2的幂值，如1、2、4、8、16、32等等。

3. Hilbert曲线算法

具体算法

(1）读入x和y坐标的n比特二进制表示。

(2）隔行扫描二进制比特到一个字符串。

(3）将字符串自左至右分成2比特长的串。

(4）规定每个2比特长的串的十进制值，例如"00"等于0,"01"等于1,"10"等于3,"11"等于2。

(5）对于数组中每个数字j，如果 j =0把后面数组中出现的所有1变成3，并把所有出现的3变成1。j =3把后面数组中出现的所有0变成2，并把所有出现的2变成0。

(6）将数组中每个值按步骤5转换成二进制表示（2比特长的串），自左至右连接所有的串，并计算其十进制值。

伪代码

下述伪代码中，函数interlaced_scanning(n, x, y)实现隔行扫描功能。输入方阵维数2的n次幂，x、y坐标。输出隔行扫描后的字符串。n要求大于等于0，x、y区间均为[0,n-1]

FUNCTION interlaced_scanning(n, x, y)     IF n >= 0 THEN         n = 2 ^ n         IF 0 <= x AND x <= n - 1 AND 0 <= y AND y <= n - 1 THEN             x1 = 将x转换为二进制字符串（去除前面的 '0b' 标识）             y1 = 将y转换为二进制字符串（去除前面的 '0b' 标识）             deta = x1的长度 - y1的长度             IF deta > 0 THEN                 y1 = 用 '0' 补齐y1使其长度与x1相同（在前面补 '0'）             ELSE IF deta < 0 THEN                 x1 = 用 '0' 补齐x1使其长度与y1相同（在前面补 '0'）             END IF             str0 = 空字符串             FOR i 从 0 到 x1的长度 - 1                 str0 = str0 + x1的第i个字符 + y1的第i个字符             END FOR             RETURN str0         END IF     END IF     RETURN False END FUNCTION

下述伪代码实现算法（4）的功能。

输入隔行扫描后的字符串，返回字符串。

FUNCTION transfer(str0)     str1 = 空字符串     FOR i 从 0 开始，每次递增2，直到str0的长度         IF str0中从i开始长度为2的子串等于 '00' THEN             str1 = str1 + '0'         ELSE IF str0中从i开始长度为2的子串等于 '01' THEN             str1 = str1 + '1'         ELSE IF str0中从i开始长度为2的子串等于 '10' THEN             str1 = str1 + '3'         ELSE IF str0中从i开始长度为2的子串等于 '11' THEN             str1 = str1 + '2'         END IF     END FOR     RETURN str1 END FUNCTION

下述伪代码实现算法（5）的功能。

输入（4）后的字符串，返回字符串。

FUNCTION transfer2(str1)     FOR j 从 0 到 str1的长度 - 1         IF str1的第j个字符等于 '0' THEN             FOR i 从 j 到 str1的长度 - 1                 IF str1的第i个字符等于 '1' THEN                     str1的第i个字符更新为 '3'                 ELSE IF str1的第i个字符等于 '3' THEN                     str1的第i个字符更新为 '1'                 END IF             END FOR         ELSE IF str1的第j个字符等于 '3' THEN             FOR i 从 j 到 str1的长度 - 1                 IF str1的第i个字符等于 '0' THEN                     str1的第i个字符更新为 '2'                 ELSE IF str1的第i个字符等于 '2' THEN                     str1的第i个字符更新为 '0'                 END IF             END FOR         END IF     END FOR     RETURN str1 END FUNCTION

下述伪代码实现算法（6）的功能。

输入（5）后的字符串，返回结果整数值。

FUNCTION transfer3(str2)     str3 = 空字符串     FOR i 从 0 到 str2的长度 - 1         IF str2的第i个字符等于 '0' THEN             str3 = str3 + '00'         ELSE IF str2的第i个字符等于 '1' THEN             str3 = str3 + '01'         ELSE IF str2的第i个字符等于 '2' THEN             str3 = str3 + '10'         ELSE IF str2的第i个字符等于 '3' THEN             str3 = str3 + '11'         END IF     END FOR     RETURN 将str3转换为十进制整数（以二进制形式解析str3转换为十进制） END FUNCTION

下述伪代码将前述四个函数进行整合，输入n,x,y，输出Hilbert映射的整数值。

FUNCTION hilbert_mapping2(n, x, y)     RETURN transfer3(transfer2(transfer(interlaced_scanning(n, x, y)))) END FUNCTION

流程图

4. Hilbert曲线算法--矩阵转置、对称、拼接

规律

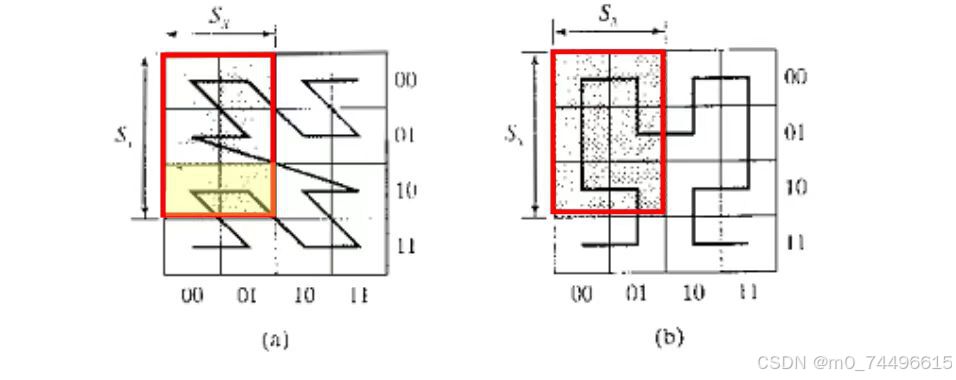
图三

以图三为例，将0-15当作一个整体，开口向上；16-31开口向左；32-47开口向左；48-63开口向下。

我发现，对于一整个方阵，可以将其视作四个小方阵组成，其中两个开口同向，另外两个开口反向。

以图三为例，二维方阵整体开口向左，四维方阵整体开口向上，八维方阵整体开口向左…得出结论：方阵开口方向交替向左向上。即两种组成方式交替。

例如：当输入一个八维方阵时，结果十六维方阵由四个八维方阵组成。可以视作四个组成单元。输入的八维方阵作为左上单元，将第一单元转置再加上64（8的平方），得到左下单元，而右下单元与左下单元同向，左下单元加上64等于右下单元，右上单元与左上单元反向，考虑数据传输方向，左上单元中心对称后再加上3*64得到右上单元。最后将四个单元合并得到十六维方阵输出。

图四

代码实现

输入Hilbert映射的n维方阵，输出得到2n维的Hilbert映射方阵。

源代码

def z_mapping(n: int, x: int, y: int):
    # 输入方阵维数2的n次幂，x、y坐标。输出z映射的值。n要求大于等于0，x、y区间均为[0,n-1]
    if n >= 0:
        n = pow(2, n)
        if 0 <= x <= n - 1 and 0 <= y <= n - 1:
            x1 = bin(x)[2:]
            y1 = bin(y)[2:]
            deta = len(x1) - len(y1)
            if deta > 0:
                y1 = '0' * deta + y1
            elif deta < 0:
                x1 = '0' * (-deta) + x1
            str0 = ''
            for i in range(len(x1)):
                str0 = str0 + x1[i] + y1[i]
            return int(str0, 2)
    return False

def interlaced_scanning(n: int, x: int, y: int):  # 输入方阵维数2的n次幂，x、y坐标。输出隔行扫描后的字符串。n要求大于等于0，x、y区间均为[0,n-1]
    if n >= 0:
        n = pow(2, n)
        if 0 <= x <= n - 1 and 0 <= y <= n - 1:
            x1 = bin(x)[2:]
            y1 = bin(y)[2:]
            deta = len(x1) - len(y1)
            if deta > 0:
                y1 = '0' * deta + y1
            elif deta < 0:
                x1 = '0' * (-deta) + x1
            str0 = ''
            for i in range(len(x1)):
                str0 = str0 + x1[i] + y1[i]
            return str0
    return False


def transfer(str0: str):
    str1 = ''
    for i in range(0, len(str0), 2):
        if str0[i:i + 2] == '00':
            str1 = str1 + '0'
        elif str0[i:i + 2] == '01':
            str1 = str1 + '1'
        elif str0[i:i + 2] == '10':
            str1 = str1 + '3'
        elif str0[i:i + 2] == '11':
            str1 = str1 + '2'
    return str1


def transfer2(str1: str):
    for j in range(len(str1)):
        if str1[j] == '0':
            for i in range(j, len(str1)):
                if str1[i] == '1':
                    str1[i] = '3'
                elif str1[i] == '3':
                    str1[i] = '1'
        elif str1[j] == '3':
            for i in range(j, len(str1)):
                if str1[i] == '0':
                    str1[i] = '2'
                elif str1[i] == '2':
                    str1[i] = '0'
    return str1


def transfer3(str2: str):
    str3 = ''
    for i in range(len(str2)):
        if str2[i] == '0':
            str3 = str3 + '00'
        elif str2[i] == '1':
            str3 = str3 + '01'
        elif str2[i] == '2':
            str3 = str3 + '10'
        elif str2[i] == '3':
            str3 = str3 + '11'
    return int(str3, 2)


# 输入方阵维数2的n次幂，x、y坐标。输出指定坐标的Hilbert映射值。n要求大于等于0，x、y区间均为[0,n-1]
def hilbert_mapping2(n: int, x: int, y: int) -> int:
    return transfer3(transfer2(transfer(interlaced_scanning(n, x, y))))


print(hilbert_mapping2(3, 5, 5))

import time
import matplotlib.pyplot as plt
import numpy as np

"""
#基本原理演示
unit0 = np.array([0])  # 0维方矩阵
unit1 = np.array([[0, 1], [3, 2]])  # 2维方矩阵-单元一

unit1T = (unit1 + 4).T  # 转置得到2维方矩阵-单元二
unit1f = np.flip(np.flip(unit1 + 3 * 2 ** 2, axis=0), axis=1)  # 先行对折，后列对折，中心对称得到2维方矩阵-单元三

unit2 = np.concatenate((np.concatenate((unit1, unit1f), axis=1), np.concatenate((unit1T, unit1T + 4), axis=1)), axis=0) #先左右合并，再上下合并
print()
print(unit2)
"""

"""
#1.0初步拼接函数编写
# 第一种拼接方法
def hilbert_mapping1(unit: np.ndarray) -> np.ndarray:
    n = len(unit)  # 获取维数n
    unit_t = (unit + n ** 2).T  # 转置得到单元二
    unit_f = np.flip(np.flip(unit + 3 * n ** 2, axis=0), axis=1)  # 先行对折，后列对折，中心对称得到单元三
    next_unit = np.concatenate(
        (np.concatenate((unit, unit_f), axis=1), np.concatenate((unit_t, unit_t + n ** 2), axis=1)),
        axis=0)  # 先左右合并，再上下合并
    return next_unit


# 第二种拼接方法
def hilbert_mapping2(unit: np.ndarray) -> np.ndarray:
    n = len(unit)  # 获取维数n
    unit_t = (unit + n ** 2).T  # 转置得到单元二
    unit_f = np.flip(np.flip(unit + 3 * n ** 2, axis=0), axis=1)  # 先行对折，后列对折，中心对称得到单元三
    next_unit = np.concatenate(
        (np.concatenate((unit, unit_f), axis=0), np.concatenate((unit_t, unit_t + n ** 2), axis=0)),
        axis=1)  # 先上下合并，再左右合并   #拼接方法一与拼接方法二仅此一处代码不同
    return next_unit
"""


# 2.0拼接方法代码优化合并，前面相同步骤共用，后面拼接步骤选择应用。
# 我们发现输入的n=2时，第一种拼接方法；n=4时，第二种；n=8时，第一种...交替进行。通过n来判定第几种方法

# 3.0又发现，第一种拼接方法与第二种拼接方法互为转置！！！
# 如果采用3.0思路，统一采用第一种拼接，之后再判断是否转置。当输入n=8，采用第一种方法拼接后还要转置，并不如先判断再直接拼接，相比之下额外多了一步转置，因此不采用3.0思路，仍选择2.0思路。
def hilbert_mapping(unit: np.ndarray) -> np.ndarray:
    n = len(unit)  # 获取维数n
    if n == 1:  # 在输入[0]时单元三对折操作与后续合并操作均出现报错，采取简单方法：对于输入[0]输出特定矩阵
        return np.array([[0, 1], [3, 2]])
    unit_t = (unit + n ** 2).T  # 转置得到单元二
    unit_f = np.flip(np.flip(unit + 3 * n ** 2, axis=0), axis=1)  # 先行对折，后列对折，中心对称得到单元三
    if np.log2(n) % 2 == 1:
        next_unit = np.concatenate(
            (np.concatenate((unit, unit_f), axis=1), np.concatenate((unit_t, unit_t + n ** 2), axis=1)),
            axis=0)  # 先左右合并，再上下合并
    else:  # elif np.log2(n) % 2 == 0:
        next_unit = np.concatenate(
            (np.concatenate((unit, unit_f), axis=0), np.concatenate((unit_t, unit_t + n ** 2), axis=0)),
            axis=1)  # 先上下合并，再左右合并
    return next_unit


"""
# [0]调试bug,以及所耗时间
a = np.array([0])
print()
t1=time.time()
for i in range(4):
    a = hilbert_mapping(a)
t2=time.time()
print(a)
print(t2-t1)
"""


def drawing(data: np.ndarray):
    # 定义热图的横纵坐标
    xLabel = []
    yLabel = []
    for i in range(len(data)):
        yLabel.append(str(i))
    for i in range(len(data[0])):
        xLabel.append(str(i))
    # 作图阶段
    fig, ax = plt.subplots(figsize=(8, 8))  # n=4时，布局8x8
    # 定义横纵坐标的刻度
    ax.set_yticks(range(len(yLabel)))
    ax.set_yticklabels(yLabel)
    ax.set_xticks(range(len(xLabel)))
    ax.set_xticklabels(xLabel)
    ax.xaxis.set_ticks_position('top')
    # 作图并选择热图的颜色填充风格，进行16分块颜色映射
    cmap = plt.get_cmap('tab20', 16)
    im = ax.imshow(data, cmap=cmap)
    # 增加右侧的颜色刻度条
    # plt.colorbar(im)

    # 填充数字
    for i in range(len(data)):
        for j in range(len(data)):
            ax.text(j, i, data[i, j], ha="center", va="center", color="black", fontsize=12)  # n=4时，字体=12

    # 增加标题
    plt.title("Hilbert Mapping", fontdict={'size': 16}, pad=30.0)
    plt.xlabel(r'X', fontdict={'size': 16}, labelpad=10.0, ha='center')

    plt.ylabel(r'Y', fontdict={'size': 16}, labelpad=10.0, rotation=0, ha='center')
    # show
    fig.tight_layout()  # 自动调整画布大小

    # plt.savefig('fig2.png')  # 替换 plt.show()

    plt.show()


a = np.array([0])
for i in range(4):
    a = hilbert_mapping(a)
drawing(a)

此文章仅作为本人平时作业的一次记录（偶然发现Hilbert的矩阵方式实现规律，很是欣喜，因此记录一下），上述内容均为原创，欢迎指正。