大学物理实验——单摆法测量重力加速度

• 实验目的 

1. 学习使用游标卡尺和螺旋测微器测量单摆摆球的直径；
2. 学习使用电子秒表，并记录单摆摆动5个周期的时间；
3. 根据不确定度均分原理，设计单摆测量重力加速度g；
4. 利用单摆测量重力加速度g。

二、实验原理       

一、单摆的一级近似的周期公式为

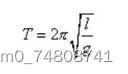
由此通过测量周期T,摆长l求重力加速度。

二、不确定度均分原理

    在间接测量中，每个独立测量的量的不确定度都会对最终结果的不确定度有贡献。如果已知各测量之间的函数关系，可写出不确定度传递公式，并按均分原理，将测量结果的总不确定度均匀分配到各个分量中，由此分析各物理量的测量方法和使用的仪器，指导实验。一般而言，这样做比较经济合理。对测量结果影响较大的物理量，应采用精度较高的仪器，而对测量结果影响不大的物理量，就不必追求高精度仪器。

三、实验仪器       

游标卡尺，螺旋测微器，米尺，单摆仪，电子停表

四、实验内容 

1、游标卡尺的使用

使用游标卡尺，测量5次单摆摆球的直径，记录数据。

2、螺旋测微计的使用

使用螺旋测微计，测量5次单摆摆球的直径，记录数据。

3、电子秒表的使用

使用电子秒表测量单摆摆动5个周期的时间，记录数据。

4、根据不确定度均分原理，设计单摆测量重力加速度g

（1）根据误差均分原理,自行设计试验方案,合理选择测量仪器和方法.

（2）测量重力加速度g,测量精度要求△g/g < 1%.

可提供的器材及参数:

游标卡尺,米尺,千分尺,电子秒表,支架,细线(尼龙线),钢球,摆幅测量标尺(提供硬白纸板自制),天平(公用).

假设摆长l≈70.00cm;摆球直径D≈2.00cm;摆动周期T≈1.700s;
米尺精度△米≈0.05cm;卡尺精度△卡≈0.002cm;千分尺精度△千≈0.001cm;秒表精度△秒≈0.01s;根据统计分析,实验人员开或停秒表反应时间为0.1s左右,所以实验人员开,停秒表总的反应时间近似为△人≈0.2s.

5、利用单摆测量重力加速度g

利用实验室提供的单摆仪，调整并确定合适的摆线长度，测量重力加速度

    

五、数据处理

（以下为内容例子）

• 数据记录

1、游标卡尺的使用

2、螺旋测微计的使用

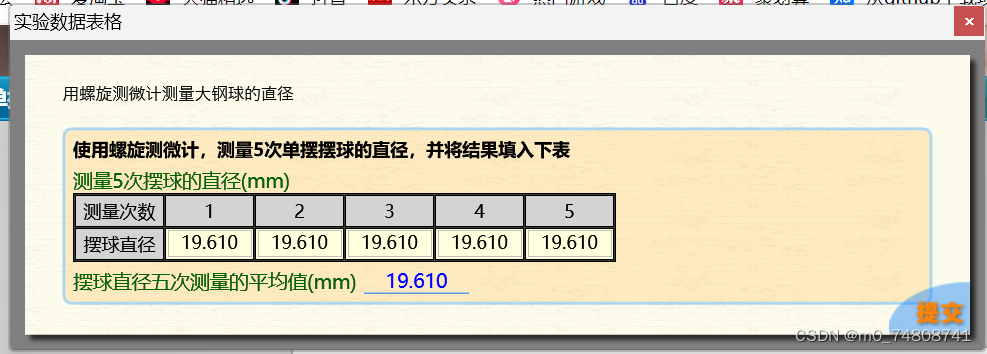
3、电子秒表的使用

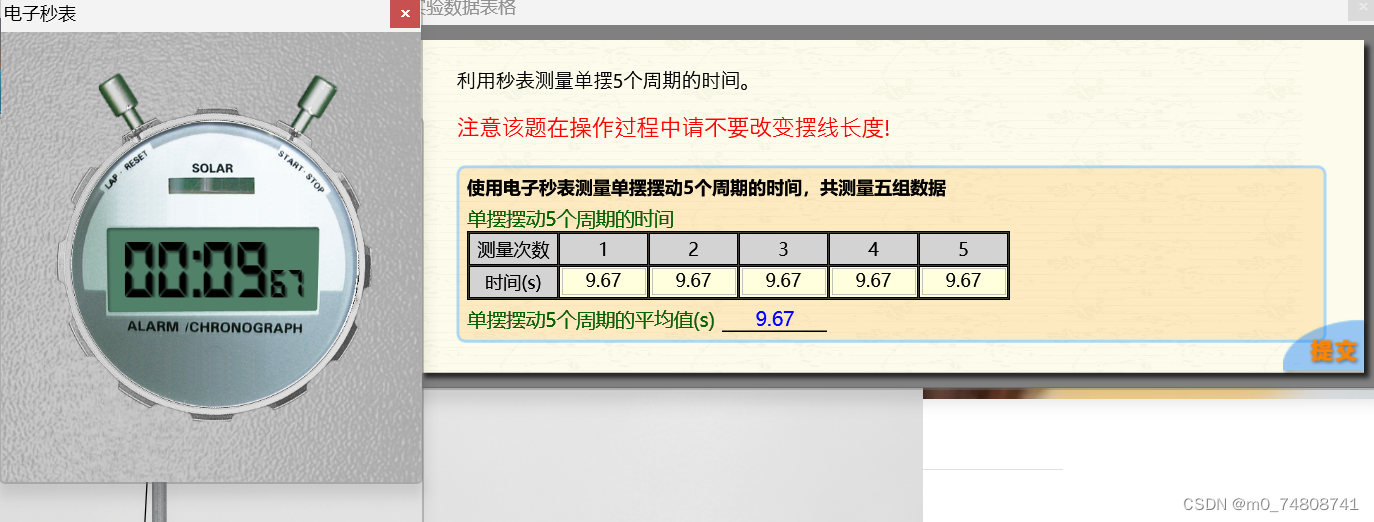
4、不确定度均分原理，设计单摆测量重力加速度g

5、利用单摆测量重力加速度g

（二）计算和数据处理

计算重力加速度g(m/s2)=(4Π2L)/(T2)=(4*3.142*0.9)/(95.91/50)2≈9.65m/s2

六、实验总结(提示：分析讨论和实验结论应分开写)

分析讨论：

1. 测量单摆周期要测量几十次，而不是一次，为什么？

分析：因为测量一次误差太大，多次测量，可以减小误差。

1. 摆长是哪两点间的距离？

分析：摆长指的是悬点到摆球球心的距离。

1. 为什么计时应以摆球通过平衡位置开始计算？

分析：在平衡点开始计时更准确，在最高点误差太大。

实验总结：

   本次实验进一步熟悉了螺旋测微器和游标卡尺的使用方法。学习了如何正确使用电子秒表。学会了如何用单摆测量重力加速度g。通过实验还得到以下结论：

1. 单摆的周期T与摆长L之间呈反比例关系，即摆长越长，周期越长。
2. 重力加速度的数值为9.65m/s2，与理论值9.8m/s2差值没有太大。