Python 和 NumPy 中的 Cholesky 分解Python 和 NumPy 中的 Cholesky 分解
我们将研究Cholesky 分解方法的 Python 实现,该方法用于某些量化金融算法。
具体来说,它出现在蒙特卡罗方法中,用于模拟具有相关变量的系统。将 Cholesky 分解应用于相关矩阵,提供下三角矩阵 L,当将其应用于不相关样本向量 u 时,会产生系统的协方差向量。因此,它与量化交易高度相关。
Cholesky 分解假设被分解的矩阵是Hermitian且正定的。由于我们只对实值矩阵感兴趣,我们可以用**对称性(即矩阵等于其自身的转置)代替 Hermitian 的性质。在适用的情况下,Cholesky 分解比 LU 分解快约 2 倍。
为了求解下三角矩阵,我们将使用Cholesky-Banachiewicz 算法。首先,我们计算主对角线上的 L 值。随后,我们计算对角线下方元素的非对角线:
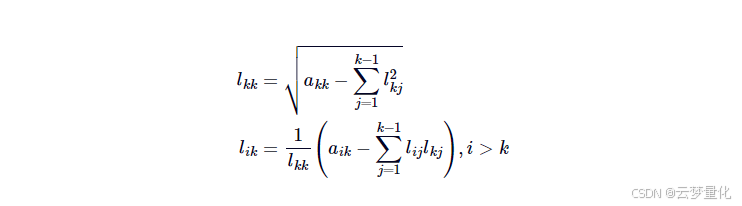
与LU 分解一样,在开发和执行时间方面最有效的方法是利用 NumPy/SciPy 线性代数 ( linalg) 库,该库具有内置的cholesky矩阵分解方法。可选lower参数允许我们确定是否生成下三角矩阵或上三角矩阵:
import pprint
import scipy
import scipy.linalg # SciPy Linear Algebra Library
A = scipy.array([[6, 3, 4, 8], [3, 6, 5, 1], [4, 5, 10, 7], [8, 1, 7, 25]])
L = scipy.linalg.cholesky(A, lower=True)
U = scipy.linalg.cholesky(A, lower=False)
print "A:"
pprint.pprint(A)
print "L:"
pprint.pprint(L)
print "U:"
pprint.pprint(U)
代码的输出如下:
A:
array([[ 6, 3, 4, 8],
[ 3, 6, 5, 1],
[ 4, 5, 10, 7],
[ 8, 1, 7, 25]])
L:
array([[ 2.44948974, 0. , 0. , 0. ],
[ 1.22474487, 2.12132034, 0. , 0. ],
[ 1.63299316, 1.41421356, 2.30940108, 0. ],
[ 3.26598632, -1.41421356, 1.58771324, 3.13249102]])
U:
array([[ 2.44948974, 1.22474487, 1.63299316, 3.26598632],
[ 0. , 2.12132034, 1.41421356, -1.41421356],
[ 0. , 0. , 2.30940108, 1.58771324],
[ 0. , 0. , 0. , 3.13249102]])
与LU 分解一样,您不太可能需要用纯 Python(即不使用 NumPy/SciPy)编写 Cholesky 分解,因为您只需包含库并使用其中更高效的实现即可。但是,为了完整性,我包含了 Cholesky 分解的纯 Python 实现,以便您了解算法的工作原理:
from math import sqrt
from pprint import pprint
def cholesky(A):
"""Performs a Cholesky decomposition of A, which must
be a symmetric and positive definite matrix. The function
returns the lower variant triangular matrix, L."""
n = len(A)
# Create zero matrix for L
L = [[0.0] * n for i in xrange(n)]
# Perform the Cholesky decomposition
for i in xrange(n):
for k in xrange(i+1):
tmp_sum = sum(L[i][j] * L[k][j] for j in xrange(k))
if (i == k): # Diagonal elements
# LaTeX: l_{kk} = \sqrt{ a_{kk} - \sum^{k-1}_{j=1} l^2_{kj}}
L[i][k] = sqrt(A[i][i] - tmp_sum)
else:
# LaTeX: l_{ik} = \frac{1}{l_{kk}} \left( a_{ik} - \sum^{k-1}_{j=1} l_{ij} l_{kj} \right)
L[i][k] = (1.0 / L[k][k] * (A[i][k] - tmp_sum))
return L
A = [[6, 3, 4, 8], [3, 6, 5, 1], [4, 5, 10, 7], [8, 1, 7, 25]]
L = cholesky(A)
print "A:"
pprint(A)
print "L:"
pprint(L)
纯 Python 实现的输出如下:
A:
[[6, 3, 4, 8], [3, 6, 5, 1], [4, 5, 10, 7], [8, 1, 7, 25]]
L:
[[2.449489742783178, 0.0, 0.0, 0.0],
[1.2247448713915892, 2.1213203435596424, 0.0, 0.0],
[1.6329931618554523, 1.414213562373095, 2.309401076758503, 0.0],
[3.2659863237109046,
-1.4142135623730956,
1.5877132402714704,
3.1324910215354165]]
SciPy 实现和纯 Python 实现都一致,尽管我们还没有计算纯 Python 实现的更高版本。在生产代码中,您应该使用 SciPy,因为它在分解较大矩阵时速度会快得多。
LU 分解方法
量化金融算法中使用的提供 NumPy/SciPy 列表以及纯 Python 列表。
解决期权定价的 Black-Scholes 偏微分方程 (PDE) 模型的关键方法之一是使用有限差分法 (FDM) 对 PDE 进行离散化,然后以数字方式求得解。某些隐式有限差分法最终会得到一组线性方程。
该线性方程组可以表述为矩阵方程,涉及矩阵一个和向量十和𝑏,其中十是要确定的解。这些矩阵通常是带状的(它们的非零元素被限制在对角线的子集中),并且使用专门的算法(例如Thomas 算法)来求解它们。
虽然从性能角度来看不是最优的,但我们将编写一种称为 LU 分解的方法,以帮助我们解决以下矩阵方程,而无需直接求逆矩阵A:

我们将利用杜立特的 LUP 分解和部分旋转来分解矩阵A进入PA=LU, 在哪里L是下三角矩阵,U是上三角矩阵,P是一个置换矩阵。P需要解决某些奇异问题。算法如下。
为了计算上三角截面,我们使用以下公式来计算元素U:

下三角矩阵元素公式大号类似,只是我们需要将每一项除以乌. 确保算法在以下情况下数值稳定你UJJ<<0,使用旋转矩阵 P 来重新排序A这样 A 中每列的最大元素就被移到A元素的公式L如下:

创建一个大号乌Python 中的分解是利用 NumPy/SciPy 库,它有一个内置方法来生成大号,乌和置换矩阵磷:
import pprint
import scipy
import scipy.linalg # SciPy Linear Algebra Library
A = scipy.array([ [7, 3, -1, 2], [3, 8, 1, -4], [-1, 1, 4, -1], [2, -4, -1, 6] ])
P, L, U = scipy.linalg.lu(A)
print "A:"
pprint.pprint(A)
print "P:"
pprint.pprint(P)
print "L:"
pprint.pprint(L)
print "U:"
pprint.pprint(U)
代码的输出如下:
A:
array([[ 7, 3, -1, 2],
[ 3, 8, 1, -4],
[-1, 1, 4, -1],
[ 2, -4, -1, 6]])
P:
array([[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]])
L:
array([[ 1. , 0. , 0. , 0. ],
[ 0.42857143, 1. , 0. , 0. ],
[-0.14285714, 0.21276596, 1. , 0. ],
[ 0.28571429, -0.72340426, 0.08982036, 1. ]])
U:
array([[ 7. , 3. , -1. , 2. ],
[ 0. , 6.71428571, 1.42857143, -4.85714286],
[ 0. , 0. , 3.55319149, 0.31914894],
[ 0. , 0. , 0. , 1.88622754]])
虽然您不太可能需要直接编写 LU 分解代码,但我提供了一个纯 Python 实现,它不依赖于任何外部库,包括 NumPy 或 SciPy。这并不是一个快速实现,事实上,它比上面概述的 SciPy 变体慢得多。此列表的目的是帮助您了解算法的“幕后”工作原理:
import pprint
def mult_matrix(M, N):
"""Multiply square matrices of same dimension M and N"""
# Converts N into a list of tuples of columns
tuple_N = zip(*N)
# Nested list comprehension to calculate matrix multiplication
return [[sum(el_m * el_n for el_m, el_n in zip(row_m, col_n)) for col_n in tuple_N] for row_m in M]
def pivot_matrix(M):
"""Returns the pivoting matrix for M, used in Doolittle's method."""
m = len(M)
# Create an identity matrix, with floating point values
id_mat = [[float(i ==j) for i in xrange(m)] for j in xrange(m)]
# Rearrange the identity matrix such that the largest element of
# each column of M is placed on the diagonal of of M
for j in xrange(m):
row = max(xrange(j, m), key=lambda i: abs(M[i][j]))
if j != row:
# Swap the rows
id_mat[j], id_mat[row] = id_mat[row], id_mat[j]
return id_mat
def lu_decomposition(A):
"""Performs an LU Decomposition of A (which must be square)
into PA = LU. The function returns P, L and U."""
n = len(A)
# Create zero matrices for L and U
L = [[0.0] * n for i in xrange(n)]
U = [[0.0] * n for i in xrange(n)]
# Create the pivot matrix P and the multipled matrix PA
P = pivot_matrix(A)
PA = mult_matrix(P, A)
# Perform the LU Decomposition
for j in xrange(n):
# All diagonal entries of L are set to unity
L[j][j] = 1.0
# LaTeX: u_{ij} = a_{ij} - \sum_{k=1}^{i-1} u_{kj} l_{ik}
for i in xrange(j+1):
s1 = sum(U[k][j] * L[i][k] for k in xrange(i))
U[i][j] = PA[i][j] - s1
# LaTeX: l_{ij} = \frac{1}{u_{jj}} (a_{ij} - \sum_{k=1}^{j-1} u_{kj} l_{ik} )
for i in xrange(j, n):
s2 = sum(U[k][j] * L[i][k] for k in xrange(j))
L[i][j] = (PA[i][j] - s2) / U[j][j]
return (P, L, U)
A = [[7, 3, -1, 2], [3, 8, 1, -4], [-1, 1, 4, -1], [2, -4, -1, 6]]
P, L, U = lu_decomposition(A)
print "A:"
pprint.pprint(A)
print "P:"
pprint.pprint(P)
print "L:"
pprint.pprint(L)
print "U:"
pprint.pprint(U)
纯 Python 实现的输出如下:
A:
[[7, 3, -1, 2], [3, 8, 1, -4], [-1, 1, 4, -1], [2, -4, -1, 6]]
P:
[[1.0, 0.0, 0.0, 0.0],
[0.0, 1.0, 0.0, 0.0],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0]]
L:
[[1.0, 0.0, 0.0, 0.0],
[0.42857142857142855, 1.0, 0.0, 0.0],
[-0.14285714285714285, 0.2127659574468085, 1.0, 0.0],
[0.2857142857142857, -0.7234042553191489, 0.0898203592814371, 1.0]]
U:
[[7.0, 3.0, -1.0, 2.0],
[0.0, 6.714285714285714, 1.4285714285714286, -4.857142857142857],
[0.0, 0.0, 3.5531914893617023, 0.31914893617021267],
[0.0, 0.0, 0.0, 1.88622754491018]]
5, 1.0, 0.0],
[0.2857142857142857, -0.7234042553191489, 0.0898203592814371, 1.0]]
U:
[[7.0, 3.0, -1.0, 2.0],
[0.0, 6.714285714285714, 1.4285714285714286, -4.857142857142857],
[0.0, 0.0, 3.5531914893617023, 0.31914893617021267],
[0.0, 0.0, 0.0, 1.88622754491018]]
您可以看到,上面的输出与 SciPy 实现生成的输出相匹配,尽管计算速度较慢。























 6549
6549

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








