统计均值回归测试基础

最新推荐文章于 2025-03-08 09:00:00 发布

云梦量化

最新推荐文章于 2025-03-08 09:00:00 发布

阅读量1.2k

点赞数 29

文章标签：均值算法 kotlin android 信息可视化算法数据分析

本文链接：https://blog.csdn.net/m0_74840398/article/details/143042583

版权

统计均值回归测试基础

到目前为止，我们在 QuantStart 上讨论了算法交易策略识别、成功的回测、证券主数据库以及如何构建软件研究环境。现在是时候将注意力转向形成实际的交易策略以及如何实施它们了。

量化工具箱中的一个关键交易概念是均值回归。此过程指的是时间序列显示出回归其历史平均值的趋势。从数学上讲，这种（连续）时间序列称为Ornstein-Uhlenbeck过程。这与随机游走（布朗运动）形成对比，后者没有“记忆”它在每个特定时间点的位置。时间序列的均值回归特性可用于制定有利可图的交易策略。

在本文中，我们将概述识别均值回归所需的统计测试。特别是，我们将研究平稳性的概念以及如何对其进行测试。

均值回归测试

连续均值回归时间序列可以用 Ornstein-Uhlenbeck 随机微分方程表示：

在这里插入图片描述

在哪里𝜃是回归均值的速度，𝜇是过程的平均值，𝜎是过程的方差，Wt是维纳过程或布朗运动。

在离散设置中，该方程表明下一时间段内价格序列的变化与平均价格和当前价格之间的差异成正比，并加上高斯噪声。

此属性激发了增强迪基-福勒检验，我们将在下面进行描述。

增强迪基-福勒 (ADF) 检验

从数学上讲，ADF 基于测试自回归时间序列样本中是否存在单位根的思想。它利用了这样一个事实：如果价格序列具有均值回归，则下一个价格水平将与当前价格水平成比例。线性滞后模型的阶数P用于时间序列：
在这里插入图片描述

在哪里𝛼是一个常数，𝛽表示时间趋势的系数，Δyt=y（t）−y（t−1）。ADF 假设检验的作用是考虑零假设𝛾=0，这将表明（𝛼=𝛽=0) 这个过程是一个随机游走过程，因此不会回归均值。

如果假设𝛾=0可以被拒绝，那么价格序列的后续变动与当前价格成比例，因此不太可能是随机游走。

那么 ADF 检验是如何进行的呢？第一个任务是计算检验统计量（D𝐹𝜏），由样本比例常数给出𝛾^除以样本比例常数的标准误差：

在这里插入图片描述

Dickey 和 Fuller 之前已经计算了该检验统计量的分布，这使我们能够确定对于任何选定的百分比临界值的假设的拒绝率。检验统计量是一个负数，因此为了在临界值之外保持显著性，该数字必须比这些值更负，即小于临界值。

对于交易者来说，一个关键的实际问题是，价格的任何长期恒定漂移都比任何短期波动的幅度小得多，因此漂移通常被假定为零（𝛽=0) 作为模型。

由于我们正在考虑顺序滞后模型页，我们需要实际设置页设置为特定值。对于交易研究来说，通常只需设置P=1让我们拒绝零假设。

要计算增强迪基-福勒检验，您需要获取 2004 年 9 月 1 日至 2020 年 8 月 31 日的 Google 开盘-最高-最低-收盘-成交量 (GOOG OHLCV) 数据的 csv。这可以从Yahoo Finance免费获得。然后我们可以使用pandas和statsmodels库。前者为我们提供了一种处理 OHLCV 数据的直接方法，而后者将 ADF 测试包装在一个易于调用的函数中。

我们将对 2004 年 9 月 1 日至 2020 年 8 月 31 日的谷歌股票样本价格序列进行 ADF 测试。

在这里插入图片描述

2004 年 9 月 1 日至 2020 年 8 月 31 日的 Google 价格系列

以下是进行测试的 Python 代码：

import pandas as pd
import statsmodels.tsa.stattools as ts

def create_dataframe(data_csv):
    """
    Read pricing data csv download for Google (GOOG)
    OHLCV data from 01/09/2004-31/08/2020 into a DataFrame.

    Parameters
    ----------
    data_csv : `csv`
        CSV file containing pricing data

    Returns
    -------
    `pd.DataFrame`
        A DataFrame containing Google (GOOG) OHLCV data from
        01/09/2004-31/08/2020. Index is a Datetime object.

    """
    # Create a pandas DataFrame containing the Google OHLCV data
    goog = pd.read_csv(data_csv, index_col="Date")
    # Convert index to a Datetime object
    goog.index = pd.to_datetime(goog.index)
    return goog


def augmented_dickey_fuller(goog):
    """
    Carry out the Augmented Dickey-Fuller test for Google data.

    Parameters
    ----------
    goog : `pd.DataFrame`
      A DataFrame containing Google (GOOG) OHLCV data from
          01/09/2004-31/08/2020. Index is a Datetime object.

    Returns
    -------
    None
    """
    # Output the results of the Augmented Dickey-Fuller test for Google
    # with a lag order value of 1
    adf = ts.adfuller(goog['Adj Close'], 1)
    print(adf)


if __name__ == "__main__":
    data_csv = "/Path/To/Your/GOOG.csv"

    goog_df = create_dataframe(data_csv)
    goog_adf = augmented_dickey_fuller(goog_df)

这是 Google 在该时间段内的 Augmented Dickey-Fuller 检验的输出。第一个值是计算出的检验统计量，第二个值是 p 值。第四个值是样本中的数据点数。第五个值（字典）分别包含 1%、5% 和 10% 处的检验统计量的临界值。有关 Augmented Dickey-Fuller 检验的此实现的完整文档可在此处找到。

(1.2593083267795873,
0.9963710920500263,
1,
4026,
{'1%': -3.4319753040982497, 
'5%': -2.8622581704258483, 
'10%': -2.56715228954666}, 
30818.361054280154)

由于检验统计量的计算值大于 1%、5% 或 10% 水平上的任何临界值，因此我们不能拒绝原假设𝛾=0因此我们不太可能找到均值回归的时间序列。

平稳性概念提供了识别均值回归时间序列的另一种方法，我们现在将对此进行讨论。

平稳性测试

如果时间序列（或随机过程）的联合概率分布在时间或空间平移下不变，则该时间序列（或随机过程）被定义为强平稳。特别是，对于交易者来说，过程的均值和方差不会随时间或空间而变化，并且它们各自不遵循趋势，这一点至关重要。

平稳价格序列的一个关键特征是，序列中的价格从其初始值扩散的速度比几何布朗运动的速度慢。通过测量这种扩散行为的速度，我们可以识别时间序列的性质。

我们现在将概述一种计算，即赫斯特指数，它有助于我们描述时间序列的平稳性。

赫斯特指数

赫斯特指数的目标是为我们提供一个标量值，帮助我们识别（在统计估计的范围内）一个序列是均值回归、随机游走还是趋势。

赫斯特指数计算背后的理念是，我们可以使用对数价格序列的方差来评估扩散行为的速度。对于任意时间滞后𝜏，方差由以下公式给出：

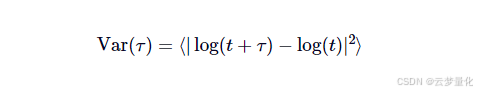
在这里插入图片描述

由于我们将扩散速率与几何布朗运动的速率进行比较，因此我们可以使用以下事实：𝜏我们认为方差与𝜏对于 GBM 来说：

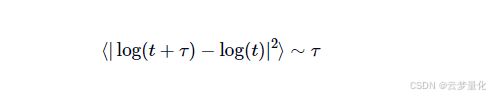
在这里插入图片描述

关键见解是，如果存在任何自相关性（即任何连续价格变动都具有非零相关性），则上述关系无效。相反，可以对其进行修改以包含指数值“2H“，这给了我们赫斯特指数值H：

在这里插入图片描述

时间序列可以用以下方式表征：

H<0.5- 时间序列呈均值回归
H=0.5- 时间序列是几何布朗运动
H>0.5- 时间序列呈趋势

除了表征时间序列之外，赫斯特指数还描述了序列在分类方式下表现的程度。例如，赫接近 0 是一个高度均值回归序列，而对于赫接近 1，该系列呈现强劲趋势。

为了计算 Google 价格序列的赫斯特指数（如上文 ADF 解释中所述），我们可以使用以下 Python 代码：

from numpy import cumsum, log, polyfit, sqrt, std, subtract
from numpy.random import randn

def hurst(ts):
    """
    Returns the Hurst Exponent of the time series vector ts

    Parameters
    ----------
    ts : `numpy.array`
        Time series upon which the Hurst Exponent will be calculated

    Returns
    -------
    'float'
        The Hurst Exponent from the poly fit output
    """
    # Create the range of lag values
    lags = range(2, 100)

    # Calculate the array of the variances of the lagged differences
    tau = [sqrt(std(subtract(ts[lag:], ts[:-lag]))) for lag in lags]

    # Use a linear fit to estimate the Hurst Exponent
    poly = polyfit(log(lags), log(tau), 1)

    # Return the Hurst exponent from the polyfit output
    return poly[0]*2.0

# Create a Gometric Brownian Motion, Mean-Reverting and Trending Series
gbm = log(cumsum(randn(100000))+1000)
mr = log(randn(100000)+1000)
tr = log(cumsum(randn(100000)+1)+1000)

# Output the Hurst Exponent for each of the above series
# and the price of Google (the Adjusted Close price) for 
# the ADF test given above in the article
print("Hurst(GBM):   %s" % hurst(gbm))
print("Hurst(MR):    %s" % hurst(mr))
print("Hurst(TR):    %s" % hurst(tr))

# Assuming you have run the above code to obtain 'goog'!
print("Hurst(GOOG):  %s" % hurst(goog['Adj Close'].values))

Hurst Exponent Python 代码的输出如下：

Hurst(GBM):   0.5031756326748011
Hurst(MR):    0.0003405749602341958
Hurst(TR):    0.9610746103704354
Hurst(GOOG):  0.4149039167976803

从这个输出我们可以看出几何布朗运动具有赫斯特指数，H，几乎正好是 0.5。均值回归序列有H几乎等于零，而趋势序列H接近于 1。

有趣的是，谷歌H也接近 0.5，表明它非常接近几何随机游动（至少对于我们利用的样本周期而言！）。

虽然我们现在有一种方法可以描述价格时间序列的性质，但我们还没有讨论这个值的*统计意义。*H是。我们需要能够确定我们是否可以拒绝原假设H=0.5确定均值回归或趋势行为。

在后续文章中，我们将描述如何计算H具有统计显著性。此外，我们将考虑协整的概念，这将使我们能够从多个不同的价格序列中创建自己的均值回归时间序列。最后，我们将把这些统计技术结合在一起，以形成一个基本的均值回归交易策略。