实Schur标准形之QR迭代法

什么是实Schur标准形

使用“方法1”来计算实Schur标准形的缺点：运算量太大，收敛速度太慢

为什么使用实Schur标准形

实矩阵的QR运算中会出现复共轭特征值，通过Am=QmRm,Am+1=RmQm所得的Am逼近的可能不是一个上三角阵，但会逼近实Schur标准形

运算量小且收敛速度快的计算实Schur标准形的方法

上Hessenberg化

step one:使用Householder将目标矩阵A化成Hessenberg矩阵

step two:对化得的Hessenberg矩阵使用n-1次Givens旋转消元，得到上三角矩阵R，即得全部特征值

step three:,时间复杂度为o(n^2)

原点位移的QR迭代法

缺点：

用在有复共轭特征值的矩阵上不能期待加速收敛作用，此时需要使用双重步位移QR迭代法

收敛效果：

上Hessemberg化和位移的使用都达到了加速收敛的效果

双重步位移的QR迭代法

基本思想：将两步原点位移的QR迭代合并为一步，以避免复数运算，实现给有复共轭特征值的矩阵A加速收敛的目的

迭代格式：

算法:

隐式QR算法

功能：判断迭代过程中产生的上Hessenberg矩阵的次对角元什么时候可以忽略不计

使用方法：满足条件,就视为0；代表机器精度，是相对误差的上限或由浮点数生成（将相对误差表示成浮点数形式然后计算出机器精度u），关于后者的详细参考徐树芳、高立、张平文的《数值线性代数》第二版的2.5.1小节

算法：

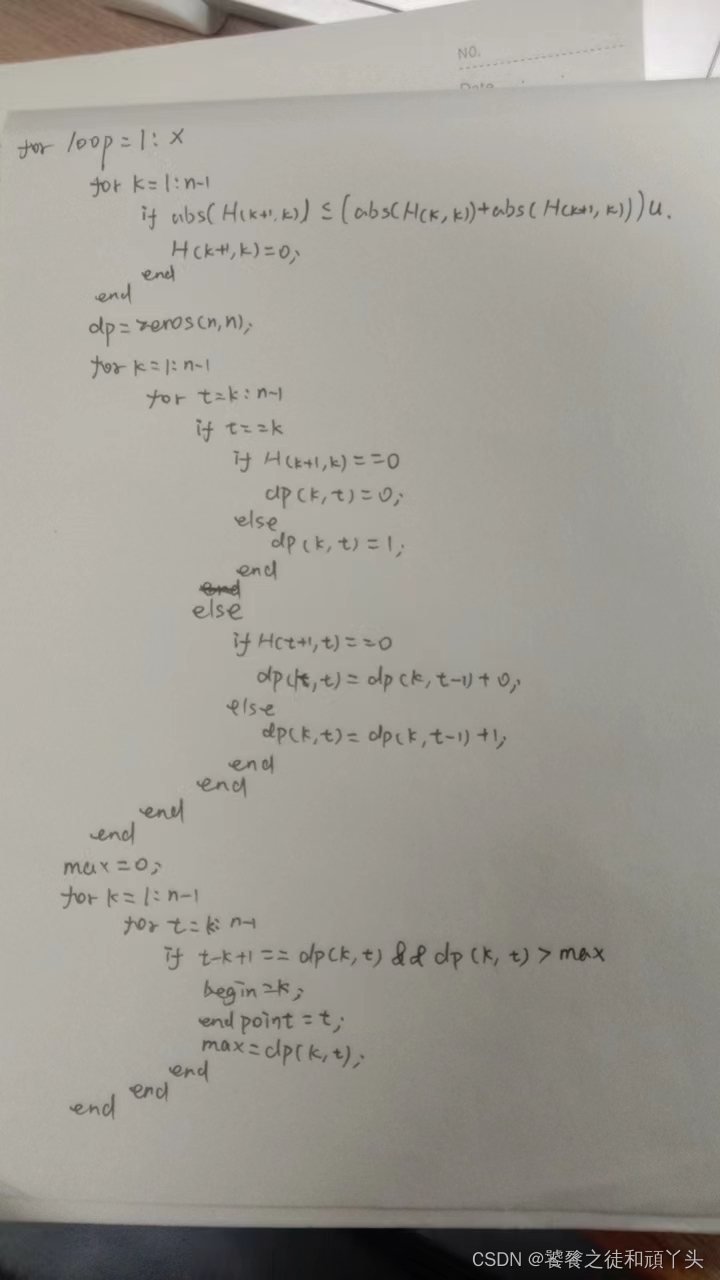
结束loop这一层循环的条件忘记加了，就是当t=k（意味着没有不可约Hessenberg矩阵）时结束loop这一层循环