目录
1. 随机事件
1.1 样本空间
S = {0, 1, 2, 3, 4, 5, 6, 7, 8}
1.2 随机事件的关系
- 和(并)事件:A∪B,A和B中至少有一个发生。
- 积(交)事件:A∩B或AB,A和B同时发生。
- 差事件:𝐴−𝐵,A发生且B不发生。
1.3 德摩根律(对偶律)
![]()
1.4 复杂事件
- A,B,C 中至少有一个发生:𝐴∪𝐵∪𝐶
- A,B,C 都发生:𝐴𝐵𝐶
- A,B,C 中恰好有两个发生:𝐴𝐵∪𝐴𝐶∪𝐵𝐶
- A,B,C 中至多有两个发生:

- A与B发生,C不发生:

2. 概率
2.1 古典概率
(1)排列: ![]()
【例】 ![]()
(2)组合: ![]()
【例】 ![]()
2.2 概率的运算性质
- 若事件A,B互斥,
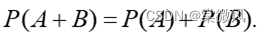
- 对任意事件A,
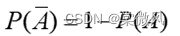
- 对任意两个事件A, B,

若![]() ,
, ![]()
- 对任意两个事件A、B,

- 若A,B相互独立,P(AB) = P(A)P(B)
【例】![]()
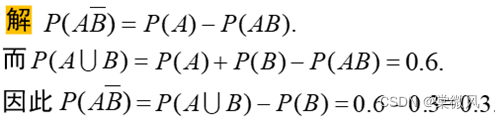
3. 条件概率
- 条件概率公式:


- 乘法公式:
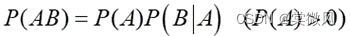
![]()
- 全概率公式:

【例】
设某人有三个不同的电子邮件账户,有70%的邮件进入账户1,另有20%的邮件进入账户2,其余10%的邮件进入账户3. 根据以往经验,三个账户垃圾邮件的比例分别为1%,2%, 5%,问某天随机收到的一封邮件为垃圾邮件的概率.

- 贝叶斯公式:

【例】
已知肝病患者经AFP检测呈阳性的概率为95%,而非肝病患者经AFP检测呈阳性(误诊)的概率为2%. 设人群中肝病的发病率为0.04%,现有一人经AFP检测呈阳性,求此人确实患肝病的概率.

4. 事件的独立性
- 若P(AB) = P(A)P(B),则事件A与事件B相互独立。
- 相互独立 不等于 互不相容。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








