医疗花费预测---数据的分布和映射

一、数据集以及影响因素

不同年龄性别的人医疗费用数据集，患者的治疗费用由诸多因素决定。如诊断、居住城市、年龄等。

import pandas as pd
import os 
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
import bokeh
import numpy as np
 
warnings.filterwarnings('ignore')
data = pd.read_csv(r'train.csv')

age：主要受益人的年龄
sex：保险承包商性别，女性，男性
bmi：体重指数，提供对身体的理解，相对于身高相对较高或较低的重量，使用身高与体重之比的体重客观指数（kg /平方公尺），理想情况下为18.5至24.9
children：健康保险覆盖的儿童人数/家属人数
smoker：吸烟
region：受益人的住宅区位于美国，东北，东南，西南，西北。
charges：由健康保险计费的个人医疗费用

二、数据分析及代码

1、查看数据集前面部分数据

data.head()

查看数据集后面部分数据

data.tail()

查看整个数据集每个特征值内是否存在空值

data.isnull().sum()

2、数据之间的关联性

from sklearn.preprocessing import LabelEncoder#LabelEncoder用于将标签（类别型数据）转换为整数编码
 
zz=LabelEncoder()#创建了一个LabelEncoder的实例，命名为zz
zz.fit(data.sex.drop_duplicates())#fit方法用于删除重复的行，确保每个类别都是唯一的
data.sex=zz.transform(data.sex)#transform方法将data.sex列中的类别数据转换为整数编码，并将转换后的数据重新赋值给data.sex列
 
zz.fit(data.smoker.drop_duplicates())
data.smoker=zz.transform(data.smoker)
 
zz.fit(data.region.drop_duplicates())
data.region=zz.transform(data.region)
 
data.corr()['charges'].sort_values()#计算data DataFrame中所有列与charges列的相关系数，并按值进行排序

将得到的结果转化为热力图

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
 
f, ax = plt.subplots(figsize=(10, 8))#创建一个图形（f）和一个坐标轴（ax），并设置图形的大小为10x8英寸
corr = data.corr()#计算data DataFrame中所有数值列的相关系数矩阵。相关系数衡量两个变量之间的线性关系，其值范围从-1到1
# 使用内置的 bool 类型替换 np.bool
sns.heatmap(corr, mask=np.zeros_like(corr, dtype=bool), cmap=sns.diverging_palette(240, 10, as_cmap=True), square=True, ax=ax)
plt.show()  # 确保添加这一行来显示图表

sns.heatmap()：这是 seaborn 库中的一个函数，用于创建热力图。
corr：这是要可视化的相关系数矩阵。
mask=np.zeros_like(corr, dtype=bool)：创建一个与 corr 形状相同且所有元素为 False 的布尔数组，用于掩码。在这里，由于所有元素都是 False，实际上不会掩码任何单元格。
cmap=sns.diverging_palette(240, 10, as_cmap=True)：设置热力图的颜色映射，使用一个从浅到深的颜色渐变。
square=True：确保每个单元格都是正方形。
ax=ax：指定在哪个轴上绘制热力图

通过上图发现医疗费用与患者是否为吸烟者有高度相关 

 三、charges的分布

3.1数据的分布

      数据分布描述了数据在不同取值区间的散布情况，它可以帮助我们了解数据的集中程度、离散程度、对称性等重要特征。这些信息对于数据清洗、特征选择、模型构建等数据处理和分析环节至关重要。常见的数据分布包括均匀分布、泊松分布、正态分布等。 

3.1.1均匀分布
        均匀分布表示数据点在一个固定范围内均匀分布，每个数据点的概率相等。连续的均匀分布密度函数为，且。在python中可以使用NumPy库的  numpy.random.uniform函数生成均匀分布的随机数。例如，要生成 10 个介于 1和 7之间的离散均匀分布随机数，可以使用以下代码：

3.1.2泊松分布

  泊松分布泊松分布描述在固定时间段或空间内，事件发生的次数。泊松分布的概率质量函数为,其中是x随机变量，表示事件发生的次数；k是事件发生的具体次数；是单位时间或空间内事件发生的平均次数，e是自然常数。泊松分布的均值和方差都等于。在python中使用NumPy库中的numpy.random.poisson函数可以生成泊松分布的随机数。要生成 10 个参数为3的泊松分布随机数，可以使用以下代码： 

3.1.3正态分布

      正态分布是一种常见的数据分布，数据点在一个固定范围内遵循正态分布。正态分布的图像呈钟形，具有对称性。其概率密度函数为u其中是均值。是标准差，决定了分布的离散程度。使用NumPy的  numpy.random.normal  函数可以生成正态分布的随机数。例如，生成 100 个均值为0，标准差为1的正态分布随机数，可以使用以下代码

3.2费用的总分布

import numpy as np
from bokeh.io import output_notebook,show
from bokeh.plotting import figure
output_notebook()
import scipy.special
from bokeh.layouts import gridplot
from bokeh.plotting import figure,show,output_file
 
p=figure(title="charges分布",tools="save",background_fill_color="#E8DDCB")
hist,edges=np.histogram(data.charges)
p.quad(top=hist,bottom=0,left=edges[:-1],right=edges[1:],fill_color="#036564",line_color="#033649")
p.xaxis.axis_label='x'
p.yaxis.axis_label='Pr(x)'
show(p)

可以看出，charges近似符合对数正态分布，所以对charges取对数，再一次进行可视化得到charges的对数，age和bmi的可视化图

3.3吸烟者与非吸烟者费用分布
 

f=plt.figure(figsize=(12,5))
ax=f.add_subplot(121)
sns.distplot(data[(data.smoker==1)]["charges"],color='c',ax=ax)
ax.set_title("Distribution of medical costs for smokers")
 
ax=f.add_subplot(122)
sns.distplot(data[(data.smoker==0)]["charges"],color='b',ax=ax)
ax.set_title("Distribution of medical costs for non-smokers")

从上图看出吸烟者在治疗上花费更多，但是查看非吸烟者的治疗花费，感觉非吸烟者的数量更多，应该好好检查一下。

 3.4 charges的对数，age和bmi的可视化图

seaborn.distplot(np.log(data['charges']))
seaborn.distplot(data['age'])
seaborn.distplot(data['bmi'])

可以从这三个图中看出，age近似服从均匀分布，所以要使用最大最小值标准化的方法将age的取值映射到区间[0,1]；charges的对数和bmi两个图近似服从正态分布，应使用z-score标准化的方法将取值映射到标准正态分布。

四、映射：

4.1、 数据映射

数据映射是指：给定两个数据模型，在模型之间建立起数据元素的对应关系，将这一过程称为数据映射。它涉及到将一种数据结构或形式转换为另一种数据结构或形式的过程。数据映射是很多数据集成任务的第一步，例如：数据迁移（data migration）、数据清洗（data cleaning）、数据集成、语义网构造、p2p信息系统。

4.2、使用字典实现映射

字典是Python中用于存储键值对的数据结构，由键（key）和值（value）组成，可以快速查找、插入和删除元素。通过字典，可以实现数据的映射。例如，可以将字符串映射到数字或其他类型的值上。

my_dict = {
    "name": "Alice",
    "age": 25,
    "city": "New York"
}

4.3、使用函数实现映射

  Python中的  map()  函数可以将一个函数应用于一个可迭代对象中的每个元素，并返回一个迭代器。这可以用来实现数据的映射

def square(x):
    return x ** 2
 
numbers = [1, 2, 3, 4, 5]
squared_numbers = map(square, numbers)
print(list(squared_numbers))

4.4、使用λ表达式

λ表达式常与  map  函数结合使用，实现数据映射。

numbers = [1, 2, 3, 4, 5]
squared_numbers = map(lambda x: x ** 2, numbers)
print(list(squared_numbers))

4.5、Pandas中的映射

Pandas是Python中非常流行的数据处理和分析库，提供了很多方便易用的数据转换和映射功能。  map()  方法是Pandas中用于数据映射的一个常用方法，它允许对Series或DataFrame中的一列进行映射转换。

import pandas as pd

# 指定文件路径，使用原始字符串来避免转义字符问题
file_path = r'C:\Users\华为\Desktop\第6章 医疗花费预测\train.csv'

# 读取CSV文件
data = pd.read_csv(file_path)

# 假设我们需要对'sex'列进行映射，将'sex'列的'female'映射为0，'male'映射为1
# 并且对'smoker'列进行映射，将'yes'映射为1，'no'映射为0
# 首先，我们需要确保这些列存在
if 'sex' in data.columns and 'smoker' in data.columns:
    # 使用map函数进行映射
    data['sex'] = data['sex'].map({'female': 0, 'male': 1})
    data['smoker'] = data['smoker'].map({'yes': 1, 'no': 0})

# 显示映射后的数据
print(data.head())

五、数据的缩放和标准化处理

5.1、MinMaxScaler

MinMaxScaler 是 sklearn.preprocessing 模块中的一个类，它用于将特征缩放到给定的最小值和最大值之间，通常是 [0, 1]。这种缩放是通过从每个特征值中减去最小值，然后除以最大值和最小值之间的差来实现的，公式如下：

其中，Xscaled是缩放后的数据，X是原始数据，Xmin和 Xmax分别是原始数据的最小值和最大值。

MinMaxScaler 的主要方法包括：

fit(X, y=None): 计算用于以后缩放的最小值和最大值。
fit_transform(X, y=None, fit_params): 拟合数据，然后对其进行转换。
transform(X): 根据 feature_range 缩放 X 的要素。
inverse_transform(X): 根据 feature_range 撤销 X 的缩放比例。
partial_fit(X, y=None): 在线计算 X 上的最小值和最大值，以便以后缩放

5.2、 StandardScaler

StandardScaler 是 sklearn.preprocessing 模块中的一个类，它用于将数据标准化到具有零均值和单位方差的标准正态分布。这种方法也被称为 Z-score 标准化。StandardScaler 的工作原理是将原始特征值减去其均值，然后除以其标准差，公式如下：

其中x是原始数据点u是均值，是标准差，z是标准化后的数据点。

StandardScaler 的主要方法包括：

fit(X, y=None): 计算训练数据的均值和标准差。
fit_transform(X, y=None, fit_params): 拟合数据，然后进行转换。
transform(X): 对新数据应用相同的标准化转换。
inverse_transform(X): 将标准化的数据转换回原始尺度。
StandardScaler 适用于数据分布接近正态分布的情况，尤其是当数据中包含异常值时。它在机器学习中非常重要，因为它可以消除不同特征之间的量纲影响，使得不同特征之间的权重变得相对平等，从而提高模型的性能和稳定性。

在实际应用中，应该根据具体的数据集和任务需求选择合适的数据预处理方法。例如，在分类、聚类算法中，需要使用距离来度量相似性的时候，或者使用PCA技术进行降维的时候，StandardScaler 表现更好。然而，如果数据的分布与正态分布差异较大，标准化可能不会达到预期的效果

5.3示例

from sklearn.preprocessing import MinMaxScaler, StandardScaler
 
min_max_scaler = MinMaxScaler()
zscore_scaler = StandardScaler()
data['charges'] = np.log(data['charges'])
data[['age']] = min_max_scaler.fit_transform(data[['age']])
data[['bmi', 'charges']] = zscore_scaler.fit_transform(data[['bmi', 'charges']])
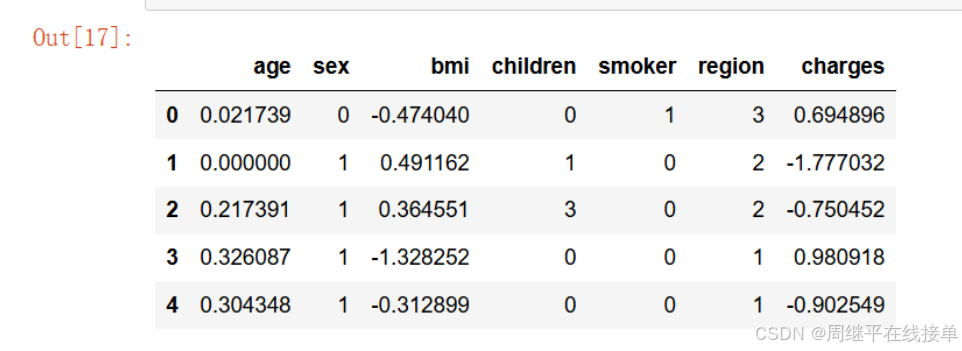
data.head(5)

结果：