正交向量
若两个n维向量a和b满足
则称向量a和向量b正交
正交矩阵
若方正A满足
则称A为正交矩阵
行向量互相正交,列向量互相正交,正交单位向量;
正交变换
A为正交矩阵,若n维向量x和y满足
则称x到y的正交变换
一维向量正交变换内积(点积)不变
二维向量(图像)的正交变换,意味着旋转
例:让A为
那么图像x顺时针旋转θ得到图像y
行列式
代数余子式
A为n阶方阵,将元素aij所在的行和列删除,剩下的n-1阶矩阵的行列式,成为元素aij的代数余子式
矩阵的逆
若方阵满足|A|不等于0,则称A为非退化方阵,或可逆矩阵
若方阵|A|=0,则称A为退化方阵
若A为非退化方阵,方阵C满足AC=I,则称C为A的逆,记作A-1
矩阵的秩
一组同维向量a1,a2,...,an,若存在不全为零的常数c1,c2,...,cn,使得:
则称该组向量线性相关
矩阵A的线性无关行向量的最大数目成为行秩,线性无关列向量的最大数目称为列秩。行秩和列秩必须相等,成为A的秩序,表示为rank(A)
特征向量和特征值
A为n阶矩阵,x为n维非零向量,λ为实数,若
则称λ为A的特征值,x为A的特征向量
可求得λ及x;其中,I为单位矩阵。
另有概念谱分解、奇异值、奇异值分解
矩阵的迹
A为n阶方阵,则它对角线元素之和称为A的迹,记作tr(A)
正定矩阵
设A是p阶对称矩阵,x是一p维向量,则x′Ax称为A的二次型
若对一切x不等于0,有x′Ax>0,则称A为正定矩阵,记作A>0
若对一切x,有x′Ax≥0,则称A为非负定矩阵,记作A≥0







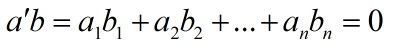
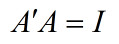
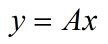
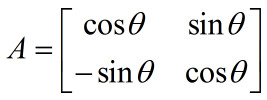
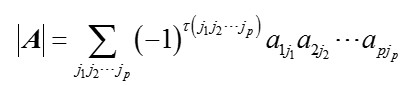
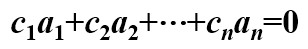
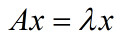
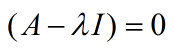














 33
33

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








