matlab机器人工具箱为Peter Corke编译的方便机器人相关计算和仿真的开源库,主要功能有机器人模型建立与仿真、正逆运动学求解、雅可比矩阵、轨迹规划、动力学等。机器人工具箱中的相关函数针对机器人开发工作的验证非常便捷,能够快速检验自己机器人运动学模型、矩阵运算是否准确。
常用功能函数可以参考文档:
MATLAB机器人工具箱【Robotics Toolbox】使用教程![]() https://ssht428.github.io/articles/matlab/robotics-4/index.html#21__27
https://ssht428.github.io/articles/matlab/robotics-4/index.html#21__27
这篇帖子仍然针对ABB的IRB2600机器人使用RTB工具箱进行运动学计算和仿真,不再对运动学相关理论进行说明。
机器人DH建模、正运动学求解及matlab代码(不依赖工具箱)可以参考这篇:
机器人运动学及轨迹规划— (2)DH建模与正运动学方程-CSDN博客![]() https://blog.csdn.net/mao3332606/article/details/140077341?spm=1001.2014.3001.5501 机器人逆运动学求解可以参考(包括全部计算过程笔记及代码):
https://blog.csdn.net/mao3332606/article/details/140077341?spm=1001.2014.3001.5501 机器人逆运动学求解可以参考(包括全部计算过程笔记及代码):
1、DH参数建模
matlab机器人工具箱建模使用到Link函数,其基于DH参数法,因此需要输入的主要参数包括theta、d、a、alpha及初始的零位偏置,下面通过MDH和SDH分别进行建模。
MDH

为了方便使用机器人工具箱,本篇机器人的6关节建立在了法兰,而第二篇为了方便进行逆解6关节建立在了腕部,因此第六个关节的theta和d是不同的,MDH参数如下所示

进行机器人建模的代码如下:
%输入MDH参数
% theta d a alpha offset
SL1=Link([0 445 0 0 0 ],'modified');
SL2=Link([0 0 150 -pi/2 0 ],'modified');
SL3=Link([0 0 700 0 0 ],'modified');
SL4=Link([0 795 115 -pi/2 0 ],'modified');
SL5=Link([0 0 0 pi/2 0 ],'modified');
SL6=Link([0 85 0 -pi/2 0 ],'modified');
%保证和实际机器人一致,初始零位偏置
SL2.offset=-pi/2;
SL6.offset=-pi;
%关节限角
SL1.qlim=[-180, 180]*pi/180;
SL2.qlim=[-95, 155]*pi/180;
SL3.qlim=[-180, 75]*pi/180;
SL4.qlim=[-400, 400]*pi/180;
SL5.qlim=[-120, 120]*pi/180;
SL6.qlim=[-400, 400]*pi/180;
%建立名为IRB2600的机器人连杆模型
IRB2600=SerialLink([SL1 SL2 SL3 SL4 SL5 SL6],'name','IRB2600');
%根据机器人模型进行示教仿真
IRB2600.teach([0 0 0 0 0 0]);代码运行结果如下:

更改机器人各个关节角度,机器人可以模拟各关节运动,同时显示笛卡尔空间对应的位置和姿态。
关于模型建立的准确性在正运动学部分再进行验证。
SDH
同一类型(结构)的机器人DH模型其实仅有关节距离和连杆长度做出区分,我找到了一篇其他博主的关于ABB-IRB4600机器人的SDH模型,我们仅需要更改下a和d然后套入自己的就好。
这是那位博主博客的参考链接:


在maltab中进行SDH建模时只需要把对应的a和d的值进行替换,运行结果与前面的MDH是完全一致的。
%输入SDH参数
% theta d a alpha offset
SL1=Link([0 445 150 -pi/2 0 ],'standard');
SL2=Link([0 0 700 0 0 ],'standard');
SL3=Link([0 0 115 -pi/2 0 ],'standard');
SL4=Link([0 795 0 pi/2 0 ],'standard');
SL5=Link([0 0 0 pi/2 0 ],'standard');
SL6=Link([0 85 0 0 0 ],'standard');
%保证和实际机器人一致,初始零位偏置
SL2.offset=-pi/2;
SL5.offset=-pi;
%关节限角
SL1.qlim=[-180, 180]*pi/180;
SL2.qlim=[-95, 155]*pi/180;
SL3.qlim=[-180, 75]*pi/180;
SL4.qlim=[-400, 400]*pi/180;
SL5.qlim=[-120, 120]*pi/180;
SL6.qlim=[-400, 400]*pi/180;
%建立名为IRB2600的机器人连杆模型
IRB2600=SerialLink([SL1 SL2 SL3 SL4 SL5 SL6],'name','IRB2600');
%根据机器人模型进行示教仿真
IRB2600.teach([0 0 0 0 0 0]);2、正运动学(FK)
在建立机器人运动学模型的基础上,给定6个关节角度值,利用fkine()函数,即可求得末端位姿矩阵。这里取与第二篇博客《DH建模与正运动学方程》相同的关节角度,可以看到通过matlab工具箱或者自己写的正运动学方程均得到了相同的位姿矩阵,且与ABB官方离线编程软件虚拟示教器一致。
%给定关节角度值
q=[60 -25 40 45 -20 60]*pi/180;
%计算该关节角度下机器人末端相对于base的位姿矩阵
T06=IRB2600.fkine([q(1) q(2) q(3) q(4) q(5) q(6)]);
%计算结果
% T06 =
% -0.6992 0.1693 0.6946 385
% 0.6781 -0.1505 0.7194 625.7
% 0.2263 0.9740 -0.0096 983.9
% 0 0 0 1
将旋转矩阵转换为ZYX欧拉角:

假如通过teach()函数发现我们在matlab建立的关节与实际机器人旋转方向相反,则需要在输入角度时给定相反值。暂时没有找到直接对运动学DH模型取反的方法(修改DH模型可以,但是没有人愿意重新建立一遍吧,而且一些机器人如KUKA的第6关节旋转方向与法兰工具坐标系tool0相反)。 假设1,4,6轴方向相反,则代码变为如下,逆运动学同理。
%给定关节角度值
q=[60 -25 40 45 -20 60]*pi/180;
%计算该关节角度下机器人末端相对于base的位姿矩阵
T06=IRB2600.fkine([-q(1) q(2) q(3) -q(4) q(5) -q(6)]);3、逆运动学(IK)
在建立机器人运动学模型的基础上,利用ikine6s或ikine进行逆运动学求解。其中ikine6s为解析解,仅能用于SDH模型,不过仍然只能得到一组解。ikine为数值解,经测试在不少点位都会产生迭代失败无法求解的问题,而设置的关节初始值对计算结果没有影响。
因此对逆解求解需求较高的话不推荐使用工具箱,6自由度的机器人建议自己计算解析解。
%指定末端位姿矩阵
T06 = [ -0.6992 0.1693 0.6946 385
0.6781 -0.1505 0.7194 625.7
0.2263 0.9740 -0.0096 983.9
0 0 0 1];
%反解机器人关节角度
InverseKinematic=IRB2600.ikine(T06);
% InverseKinematic*57.3
% 60.0031 -24.9962 40.0009 44.9890 -20.0032 60.0176当我使用MDH模型时,提示只有SDH可以使用ikine6s。
![]()
当我使用SDH时,仍然报错,提示以下内容。我们的ABB机器人是满足封闭解的条件的,而针对我建立的另外一款6轴工业机器人SDH,该函数是可以正常运行的。因此推测是建立的“这一个”SDH模型不满足该函数的条件。
![]()
4、机器人轨迹规划仿真
关节空间轨迹规划及仿真
在建立机器人运动学模型的基础上,通过jtraj()函数进行关节空间的轨迹规划,给定机器人初始和结束时的关节值,调用工具箱进行关节多项式插值,然后通过plot()函数进行绘制和仿真,代码如下:
q0 = [-90 30 0 0 30 0 ]*pi/180;%起始点
q1 = [ 60 -25 40 45 -20 60]*pi/180;%终止点
step = 50;%步长
[q,qd,qdd] = jtraj(q0,q1,step);%q,qd,qdd分别为角位移,角速度,角加速度
T=IRB2600.fkine(q);%T为各关节多项式插值点处的位姿矩阵
TT=T.T;%将T的数据集转换为三维数组
%将三维数组提取为二维矩阵,绘制末端轨迹
plot3(squeeze(TT(1,4,:)),squeeze(TT(2,4,:)),squeeze(TT(3,4,:)));
IRB2600.plot(q)%机器人运动动画仿真
%%绘制角位移、速度、加速度与时间的关系曲线
i = 1:6;
%在一个绘图窗口排列多个图片,窗口图片划分为1行3列,1为第一张图
subplot(1,3,1);
plot(q(:,i));
grid on;
title('角位移');
subplot(1,3,2);
plot(qd(:,i));
grid on;
title('角速度');
subplot(1,3,3);
plot(qdd(:,i));
grid on;
title('角加速度');机器人在关节空间运动动画及关节角位移、速度、加速度变化图如下:
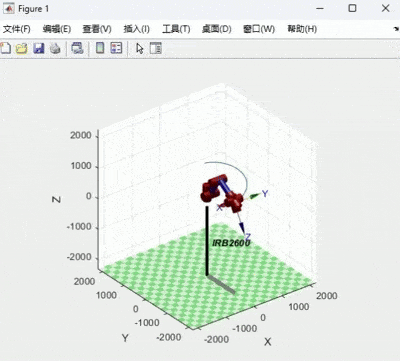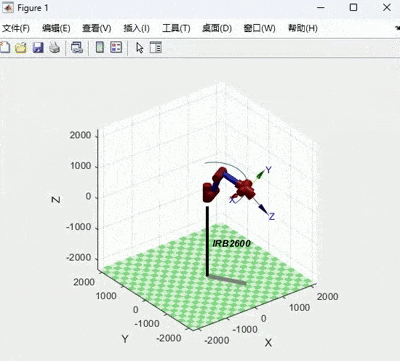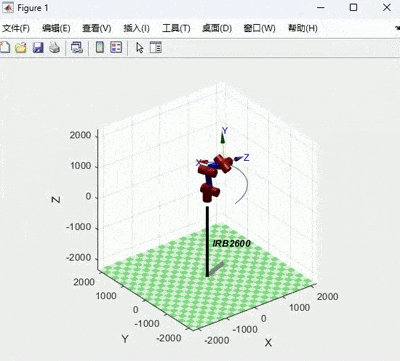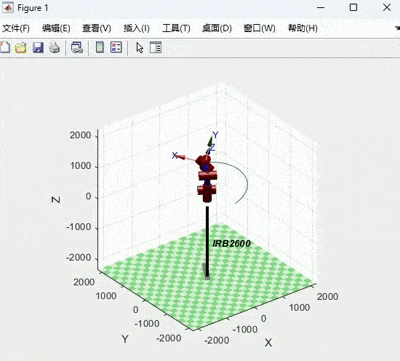

笛卡尔空间轨迹规划及仿真
对于机器人末端运动过程有需求的仿真,需要在笛卡尔空间进行轨迹规划,用到的工具箱函数为ctraj()。机器人笛卡尔空间轨迹规划需要用到逆运动学,由于机器人工具箱的ikine逆解函数不适用,因此我们使用自己反变换法得到的解析解来求逆,逆解求解的推导过程可以参考开头给出的博客链接,我也会在下面给出相应代码和使用方法。
实现机器人在笛卡尔空间轨迹规划的具体步骤如下:
1、由MDH法建立机器人运动学模型。
2、给定机器人初始和结束时的位姿矩阵(一般确定加工任务后可以通过XYZABC求得,这里暂时给出关节角度由正运动学得到),通过笛卡尔空间插值得到50个位姿矩阵,工具箱FK得到的数据类型为SE3,无法直接使用。

点开后可以看到SE3的数据是以向量的形式储存的。

需要将该数据类型进行转换:
T=double(T);%将数据类型由50个SE3转换为50个4*4矩阵转换之后的形式为:

3、由于机器人工具箱逆解函数的局限性,我们通过自己编写的逆解算法将在笛卡尔空间插补得到的50组位姿矩阵分别求逆,最终得到50组关节角度。
首先在matlab目录下创建如图所示的文件,作为逆解子程序:

然后在ikine.m文件中输入代码如下:
function IK=ikine(T06)
MDH=[0 445 0 0;
0 0 150 -pi/2;
0 0 700 0;
0 795 115 -pi/2;
0 0 0 pi/2;
0 0 0 -pi/2];
nx=T06(1,1); ny=T06(2,1); nz=T06(3,1);
ox=T06(1,2); oy=T06(2,2); oz=T06(3,2);
ax=T06(1,3); ay=T06(2,3); az=T06(3,3);
wx=T06(1,4); wy=T06(2,4); wz=T06(3,4);
d1=445; d4=795;
a1=150; a2=700; a3=115;
%t1
t11=atan2(wy,wx);
t12=atan2(-wy,-wx);
%t2
k11=wx/cos(t11)-a1;
k12=wx/cos(t12)-a1;
k3=wz-d1;
K11=(k11*k11+k3*k3+a2*a2-d4*d4-a3*a3)/2/a2;
K12=(k12*k12+k3*k3+a2*a2-d4*d4-a3*a3)/2/a2;
t21=atan2(K11/(sqrt(k11*k11+k3*k3)),sqrt((k11*k11+k3*k3-K11*K11)/(k11*k11+k3*k3)))-atan2(k3,k11);
t22=atan2(K12/(sqrt(k12*k12+k3*k3)),sqrt((k12*k12+k3*k3-K12*K12)/(k12*k12+k3*k3)))-atan2(k3,k12);
t23=atan2(K11/(sqrt(k11*k11+k3*k3)),-sqrt((k11*k11+k3*k3-K11*K11)/(k11*k11+k3*k3)))-atan2(k3,k11);
t24=atan2(K12/(sqrt(k12*k12+k3*k3)),-sqrt((k12*k12+k3*k3-K12*K12)/(k12*k12+k3*k3)))-atan2(k3,k12);
%t3
A1=(a3*(k11-a2*sin(t21))-d4*(k3-a2*cos(t21)))/(d4*d4+a3*a3);
B1=(a3*(k3-a2*cos(t21))+d4*(k11-a2*sin(t21)))/(d4*d4+a3*a3);
A2=(a3*(k12-a2*sin(t22))-d4*(k3-a2*cos(t22)))/(d4*d4+a3*a3);
B2=(a3*(k3-a2*cos(t22))+d4*(k12-a2*sin(t22)))/(d4*d4+a3*a3);
A3=(a3*(k11-a2*sin(t23))-d4*(k3-a2*cos(t23)))/(d4*d4+a3*a3);
B3=(a3*(k3-a2*cos(t23))+d4*(k11-a2*sin(t23)))/(d4*d4+a3*a3);
A4=(a3*(k12-a2*sin(t24))-d4*(k3-a2*cos(t24)))/(d4*d4+a3*a3);
B4=(a3*(k3-a2*cos(t24))+d4*(k12-a2*sin(t24)))/(d4*d4+a3*a3);
t31=atan2(A1,B1)-t21;
t32=atan2(A2,B2)-t22;
t33=atan2(A3,B3)-t23;
t34=atan2(A4,B4)-t24;
%t5
r51=ax*cos(t11)*cos(t21+t31)-az*sin(t21+t31)+ay*sin(t11)*cos(t21+t31);
r52=ax*cos(t12)*cos(t22+t32)-az*sin(t22+t32)+ay*sin(t12)*cos(t22+t32);
r53=ax*cos(t11)*cos(t23+t33)-az*sin(t23+t33)+ay*sin(t11)*cos(t23+t33);
r54=ax*cos(t12)*cos(t24+t34)-az*sin(t24+t34)+ay*sin(t12)*cos(t24+t34);
t51=atan2(-sqrt(1-r51*r51),r51);
t52=atan2(-sqrt(1-r52*r52),r52);
t53=atan2(-sqrt(1-r53*r53),r53);
t54=atan2(-sqrt(1-r54*r54),r54);
t55=atan2(sqrt(1-r51*r51),r51);
t56=atan2(sqrt(1-r52*r52),r52);
t57=atan2(sqrt(1-r53*r53),r53);
t58=atan2(sqrt(1-r54*r54),r54);
%t4
t41=atan2(ax*sin(t11)-ay*cos(t11),ax*cos(t11)*sin(t21+t31)+az*cos(t21+t31)+ay*sin(t11)*sin(t21+t31));
t42=atan2(ax*sin(t12)-ay*cos(t12),ax*cos(t12)*sin(t22+t32)+az*cos(t22+t32)+ay*sin(t12)*sin(t22+t32));
t43=atan2(ax*sin(t11)-ay*cos(t11),ax*cos(t11)*sin(t23+t33)+az*cos(t23+t33)+ay*sin(t11)*sin(t23+t33));
t44=atan2(ax*sin(t12)-ay*cos(t12),ax*cos(t12)*sin(t24+t34)+az*cos(t24+t34)+ay*sin(t12)*sin(t24+t34));
t45=atan2(-(ax*sin(t11)-ay*cos(t11)),-(ax*cos(t11)*sin(t21+t31)+az*cos(t21+t31)+ay*sin(t11)*sin(t21+t31)));
t46=atan2(-(ax*sin(t12)-ay*cos(t12)),-(ax*cos(t12)*sin(t22+t32)+az*cos(t22+t32)+ay*sin(t12)*sin(t22+t32)));
t47=atan2(-(ax*sin(t11)-ay*cos(t11)),-(ax*cos(t11)*sin(t23+t33)+az*cos(t23+t33)+ay*sin(t11)*sin(t23+t33)));
t48=atan2(-(ax*sin(t12)-ay*cos(t12)),-(ax*cos(t12)*sin(t24+t34)+az*cos(t24+t34)+ay*sin(t12)*sin(t24+t34)));
%t6
t61=atan2(ox*cos(t11)*cos(t21+t31)-oz*sin(t21+t31)+oy*sin(t11)*cos(t21+t31),-(nx*cos(t11)*cos(t21+t31)-nz*sin(t21+t31)+ny*sin(t11)*cos(t21+t31)));
t62=atan2(ox*cos(t12)*cos(t22+t32)-oz*sin(t22+t32)+oy*sin(t12)*cos(t22+t32),-(nx*cos(t12)*cos(t22+t32)-nz*sin(t22+t32)+ny*sin(t12)*cos(t22+t32)));
t63=atan2(ox*cos(t11)*cos(t23+t33)-oz*sin(t23+t33)+oy*sin(t11)*cos(t23+t33),-(nx*cos(t11)*cos(t23+t33)-nz*sin(t23+t33)+ny*sin(t11)*cos(t23+t33)));
t64=atan2(ox*cos(t12)*cos(t24+t34)-oz*sin(t24+t34)+oy*sin(t12)*cos(t24+t34),-(nx*cos(t12)*cos(t24+t34)-nz*sin(t24+t34)+ny*sin(t12)*cos(t24+t34)));
t65=atan2(-(ox*cos(t11)*cos(t21+t31)-oz*sin(t21+t31)+oy*sin(t11)*cos(t21+t31)),(nx*cos(t11)*cos(t21+t31)-nz*sin(t21+t31)+ny*sin(t11)*cos(t21+t31)));
t66=atan2(-(ox*cos(t12)*cos(t22+t32)-oz*sin(t22+t32)+oy*sin(t12)*cos(t22+t32)),(nx*cos(t12)*cos(t22+t32)-nz*sin(t22+t32)+ny*sin(t12)*cos(t22+t32)));
t67=atan2(-(ox*cos(t11)*cos(t23+t33)-oz*sin(t23+t33)+oy*sin(t11)*cos(t23+t33)),(nx*cos(t11)*cos(t23+t33)-nz*sin(t23+t33)+ny*sin(t11)*cos(t23+t33)));
t68=atan2(-(ox*cos(t12)*cos(t24+t34)-oz*sin(t24+t34)+oy*sin(t12)*cos(t24+t34)),(nx*cos(t12)*cos(t24+t34)-nz*sin(t24+t34)+ny*sin(t12)*cos(t24+t34)));
IK=[t11 t21 t31 t45 t55 t65];%仅取一组逆解
% IK=[ t11 t21 t31 t41 t51 t61
% t12 t22 t32 t42 t52 t62
% t11 t23 t33 t43 t53 t63
% t12 t24 t34 t44 t54 t64
% t11 t21 t31 t45 t55 t65
% t12 t22 t32 t46 t56 t66
% t11 t23 t33 t47 t57 t67
% t12 t24 t34 t48 t58 t68];我们IRB2600机器人正常求逆应该得到8组逆解,然而在机器人运行过程中为了保证各关节平滑稳定过渡,仅取一组关节配置来控制机器人运动。
4、在matlab命令行窗口中输入下面的主程序,将50组关节角度作为仿真输入,得到机器人在笛卡尔空间运动的连续轨迹和动画。
机器人在笛卡尔空间轨迹规划及仿真的主程序如下:
由于DH建模的关系,我们正运动学FK求解得到的位姿矩阵在法兰,而逆解函数6轴是在腕部,因此需要右乘一个transT的逆矩阵转换到腕部。
%%%%%建立机器人模型
% theta d a alpha offset
SL1=Link([0 445 0 0 0 ],'modified');
SL2=Link([0 0 150 -pi/2 0 ],'modified');
SL3=Link([0 0 700 0 0 ],'modified');
SL4=Link([0 795 115 -pi/2 0 ],'modified');
SL5=Link([0 0 0 pi/2 0 ],'modified');
SL6=Link([0 85 0 -pi/2 0 ],'modified');
%保证和实际机器人一致,初始零位偏置
SL2.offset=-pi/2;
SL6.offset=-pi;
%关节限角
SL1.qlim=[-180, 180]*pi/180;
SL2.qlim=[-95, 155]*pi/180;
SL3.qlim=[-180, 75]*pi/180;
SL4.qlim=[-400, 400]*pi/180;
SL5.qlim=[-120, 120]*pi/180;
SL6.qlim=[-400, 400]*pi/180;
%建立名为IRB2600的机器人连杆模型
IRB2600=SerialLink([SL1 SL2 SL3 SL4 SL5 SL6],'name','IRB2600');
%%%%%笛卡尔空间轨迹规划
q0 = [-70 30 10 10 30 -170 ]*pi/180;%起始点
T0=IRB2600.fkine(q0);%计算起始点位姿矩阵
q1 = [ 30 20 10 -60 80 -40 ]*pi/180;%目标点
T1=IRB2600.fkine(q1);%计算目标点位姿矩阵
step=50;%起始点到目标点的插补次数
T = ctraj(T0, T1, step);%笛卡尔空间插值
T=double(T);%将数据类型由50个SE3转换为50个4*4矩阵
q=zeros(1,6,50);%创建50个1行6列的初始化数组,用于保存逆解得到的关节角度值
%初始化XYZABC数据
X=zeros(1,50);
Y=zeros(1,50);
Z=zeros(1,50);
A=zeros(1,50);
B=zeros(1,50);
C=zeros(1,50);
%自己写的ikine逆解6轴建立在了腕部,需要做转换
transT=[-1 0 0 0
0 -1 0 0
0 0 1 85
0 0 0 1];
for i=1:50
TT=T(:,:,i);%循环提取笛卡尔空间插补得到的数组中的位姿矩阵
%记录每个插补点的XYZABC
X(i)=TT(1,4);
Y(i)=TT(2,4);
Z(i)=TT(3,4);
A(i)=atan2(TT(2,1), TT(1,1))*57.3;%旋转矩阵转ZYX欧拉角
B(i)=atan2(-TT(3,1), sqrt(TT(3,2) ^ 2 + TT(3,3) ^ 2))*57.3;
C(i)=atan2(TT(3,2), TT(3,3))*57.3;
T06=TT*inv(transT);%将FK求得的法兰位姿矩阵转换到腕部
q(:,:,i)=ikine(T06);%对位姿矩阵求逆,得到关节角度
end
%将三维数组转换为50行6列的矩阵(50组由逆解得到的关节值)
q=squeeze(q).';
%绘制末端轨迹
plot3(squeeze(T(1,4,:)),squeeze(T(2,4,:)),squeeze(T(3,4,:)),'r');
%机器人笛卡尔空间运动动画仿真
IRB2600.plot(q)
%%%%%绘制机器人XYZABC随时间变化曲线
j=1:50;%共有j个插补点
subplot(1,2,1);
plot(j,X,'r');%以j为横坐标,X为纵坐标绘图
hold on;
plot(j,Y,'g');
hold on;
plot(j,Z,'b');
hold on;
title('位移');
subplot(1,2,2);
plot(j,A,'r');
hold on;
plot(j,B,'g');
hold on;
plot(j,C,'b');
hold on;
title('角度');运行结果如下:
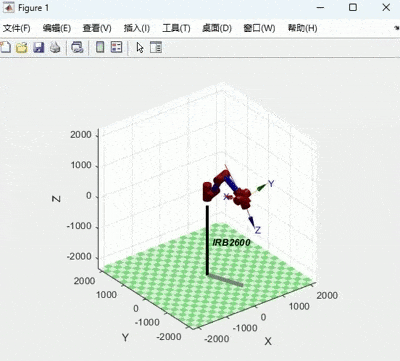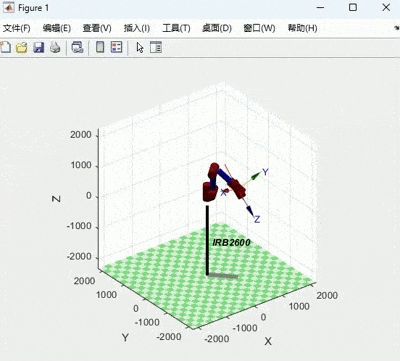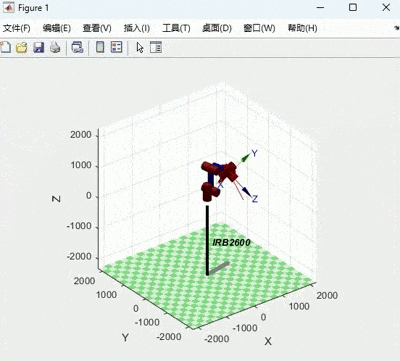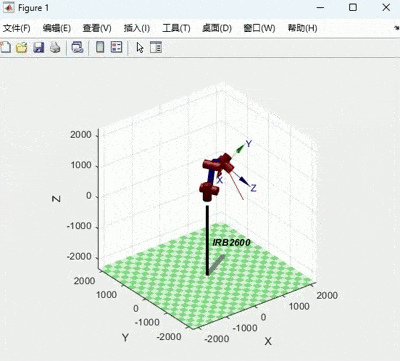

X:红 :A
Y:绿 :B
Z:蓝 :C
























 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










