第十三章 稀疏线性模型
13.1 简介
关于特征选择这个话题,其实我们在3.5.4中曾提到过,在那个方法中,我们会选择输入变量和输出的互信息很高的那些变量。这种方法的问题在于目光短浅,每次只关注一个变量。但是如果我们的变量相互之间是有联系的就不行了,比如说,如果![]() ,无论是
,无论是![]() 或者是
或者是![]() 都和结果的关系不是很大,但是异或的结果却和输出是一致的。
都和结果的关系不是很大,但是异或的结果却和输出是一致的。
在本章中,我们将着重于使用基于模型的方法一次性的选择一组变量。如果我们的模型是广义线性模型:![]() ,我们通过鼓励
,我们通过鼓励![]() 是稀疏的(有很多项是0)来进行特征的选择,这种方法提供了显著的计算优势,我们将在下面看到。
是稀疏的(有很多项是0)来进行特征的选择,这种方法提供了显著的计算优势,我们将在下面看到。
下面是特征选择/稀疏性非常有用的一些例子:
- 在许多问题中,我们的特征的数目D远大于我们的训练样本数N。对应的矩阵就是胖矩阵,而不是瘦矩阵。这个就叫做N小D大问题,这样的问题很容易导致过拟合。所以我们就要降低特征也就是D的数目。而且在这个时代这样的现象越来越多,因为我们的传感器越来越丰富,所能够获得的信息的维度越来越高。
- 在十四章中我们会讲到一个 sparse kernal machine 方法。
- 在信号处理中,常用小波基函数表示信号(图像、语音等)。为了节省时间和空间,找到信号的稀疏表示形式是有用的,这种稀疏表示形式是用少量的这种基函数表示的。这使我们能够从少量的测量中估计信号,以及压缩信号。13.8.3会进一步提到。
因此我们可以看到特征选择和稀疏性是当前机器学习/统计中最活跃的领域之一。在本章中,我们只对主要结果进行了概述。
13.2 贝叶斯变量选择
关于变量选择问题的一个很自然的想法就是引入隐变量![]() ,当
,当![]() ,我们就说第j个特征与输出是相关的,
,我们就说第j个特征与输出是相关的,![]() 则相反。那么我们模型的后验分布就是:
则相反。那么我们模型的后验分布就是:
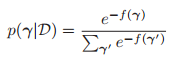
其中![]() 称为代价函数(这里把
称为代价函数(这里把![]() 代入到上面的式子中就很容易看出来上面的式子是后验分布了):
代入到上面的式子中就很容易看出来上面的式子是后验分布了):
![]()
举个例子,假设我们从线性回归模型![]() ,其中
,其中![]() (特征的数目是10)以及
(特征的数目是10)以及![]() (
(![]() 其中有五个量是等于0),生成
其中有五个量是等于0),生成![]() 个样本。事实上,我们的
个样本。事实上,我们的![]() 以及
以及![]()
![]() 。很显然我们的模型有
。很显然我们的模型有![]() ,我们分别计算每一个的后验
,我们分别计算每一个的后验![]() ,我们用格雷码的方式对模型进行排序(相邻的编码只有一个bit是不一样的)。
,我们用格雷码的方式对模型进行排序(相邻的编码只有一个bit是不一样的)。

上图的左边是格雷码的编码方式,右边是模型的cost function![]() ,我们看到这个目标函数是非常颠簸的,如果我们计算模型的后验分布
,我们看到这个目标函数是非常颠簸的,如果我们计算模型的后验分布![]() ,结果更容易解释。
,结果更容易解释。

上图的左边就是后验分布,我们取后验值最大的前八个模型:
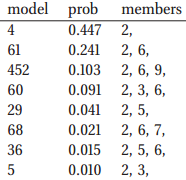
根据生成数据的模型,我们知道我们的真实模型其实是![]() ,但是特征3和8的系数相比于噪声而言是比较小的,所以这两个量就比较难以检测。如果我们有足够的数据的化,那么我们的结果就会收敛到真实的模型,但是对于有限的数据,通常会有相当大的后验不确定性。
,但是特征3和8的系数相比于噪声而言是比较小的,所以这两个量就比较难以检测。如果我们有足够的数据的化,那么我们的结果就会收敛到真实的模型,但是对于有限的数据,通常会有相当大的后验不确定性。
由于模型的数目太多了,所以用后验分布来解释会非常的complex,所以我们需要寻求一些统计量,一个比较自然的就是MAP估计,也就是得到后验的众数,但是这样的量会丢失掉模型的分布信息。所以另一种相对好一点的方法是中值模型(median model),其计算方法是:![]()
这需要计算后边缘包含概率:![]() ,上面的图(d)就是这个计算结果。我们看到,模型对包含变量2和6很有信心。如果我们将决策阈值降低到0.1,我们也会添加3和9。然而,如果我们想要捕获变量8,我们将会把5和7也加进来。关于这个折中在5.7.2.1中有讨论,画关于阈值的ROC曲线。
,上面的图(d)就是这个计算结果。我们看到,模型对包含变量2和6很有信心。如果我们将决策阈值降低到0.1,我们也会添加3和9。然而,如果我们想要捕获变量8,我们将会把5和7也加进来。关于这个折中在5.7.2.1中有讨论,画关于阈值的ROC曲线。
上面的例子说明了变量选择的黄金标准:但是往往我们的模型是稀疏的时候,D都是很大的,这就意味着我们要穷举![]() ,才能把后验分布计算出来,这是一个非常庞大的计算量,因此,我们将花费本章的大部分时间集中在算法加速上。但是在我们这么做之前,我们先解释上面例子的
,才能把后验分布计算出来,这是一个非常庞大的计算量,因此,我们将花费本章的大部分时间集中在算法加速上。但是在我们这么做之前,我们先解释上面例子的![]() 是如何进行计算的。
是如何进行计算的。
13.2.1 The spike(钉) and slab(厚板) model
我们知道后验正比于先验乘以似然:![]() ,我们先来看先验,然后再去看似然。一般来说,对于1bit的向量,我们使用如下的先验:
,我们先来看先验,然后再去看似然。一般来说,对于1bit的向量,我们使用如下的先验:
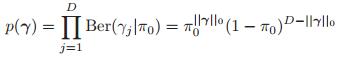
其中![]() 是每一个变量相关的可能性,其实就是稀疏性,越小越稀疏。那么我们的log似然具有如下的形式:
是每一个变量相关的可能性,其实就是稀疏性,越小越稀疏。那么我们的log似然具有如下的形式:
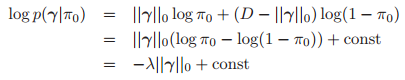
其中![]() 控制着模型的稀疏性。
控制着模型的稀疏性。
我们的似然函数可以写成如下的形式:
![]()
为了符号的简洁,我们假设假设数据的均值是0,这样![]() 这个先验就省去了均值参数。
这个先验就省去了均值参数。
我们先讨论先验![]() ,如果
,如果![]() ,说明特征j是不相关的,所以我们则希望
,说明特征j是不相关的,所以我们则希望![]() ,相反
,相反![]() ,我们则希望
,我们则希望![]() 是非0的。如果我们标准化输入(这里应该指输入的scalar都是一样的),那么我们的先验就是
是非0的。如果我们标准化输入(这里应该指输入的scalar都是一样的),那么我们的先验就是![]() ,
,![]() 表明我们希望相关变量的系数到底多大。综上,那么我们的先验如下:
表明我们希望相关变量的系数到底多大。综上,那么我们的先验如下:
![]()
第一项就是delta函数,表明在原点有个峰,对于第二项,如果![]() ,那么
,那么![]() 就会接近于均匀分布,可以被认为是一个恒定高度的平板,所以我们称之为spike and slab model。对于
就会接近于均匀分布,可以被认为是一个恒定高度的平板,所以我们称之为spike and slab model。对于![]() 这些特征,我们其实是完全可以扔掉的,所以似然可以改写为:
这些特征,我们其实是完全可以扔掉的,所以似然可以改写为:
![]()
其中![]() 。我们定义先验为
。我们定义先验为![]() ,其中
,其中![]() 是任意的正定矩阵(我们经常使用g-prior,即
是任意的正定矩阵(我们经常使用g-prior,即![]() ,ridge regression,可以用CV,经验贝叶斯,多层贝叶斯来估计g)。
,ridge regression,可以用CV,经验贝叶斯,多层贝叶斯来估计g)。
有了这些先验之后,我们就可以计算相应的边缘似然函数了,我们假设噪声方差是已知的,那么计算公式如下:

关于这个的计算,我们通过公式4.126可以得到。
如果噪声的方差是不知道的,那么我们可以通过积分的方式将其积掉。我们经常使用![]() ,这是方差的共轭先验,关于a和b 的选择可以参照
,这是方差的共轭先验,关于a和b 的选择可以参照![]() 。如果我们使用
。如果我们使用![]() ,那么这就是jeffrey‘s 先验
,那么这就是jeffrey‘s 先验![]() ,也就是无信息的先验。所以我们的最终积分后的边缘似然如下(具体可以参照
,也就是无信息的先验。所以我们的最终积分后的边缘似然如下(具体可以参照![]() ):
):

其中![]() 。
。
当我们的边缘似然并不能通过积分计算得到,即没有闭式表达式(比如我们使用logistic回归,或者非线性模型时),那么我们就使用BIC准则来做近似,具体形式如下:
![]()
其中![]() 是最大似然或者是ML的计算结果,当然是基于
是最大似然或者是ML的计算结果,当然是基于![]() 的。当然我们也可以把似然加上去,那么我们的目标函数就是:
的。当然我们也可以把似然加上去,那么我们的目标函数就是:
![]()
我们可以看到这里有两个惩罚项:一个是对于边缘似然的BIC近似,另一项则是由于先验导致的。当然很明显这两项可以合并的,所以我们就用![]() 来表示。
来表示。
13.2.2 从伯努利-高斯模型到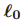 正则化
正则化
另一个我们有时会使用的模型如下:
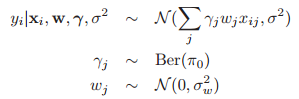
在信号处理领域,我们叫这个为伯努利-高斯模型,尽管我们有时也称它为binary mask模型。
从参数模型上,我们好像觉得这个模型与之前的spike和slab模型是一样的,但是从概率模型来看这个并不是一样,在伯努利-高斯模型中,模型是![]() ,然而spike and slab模型是
,然而spike and slab模型是![]()
这个模型很有趣的就是他可以用来推导一个非贝叶斯的模型,而且在很多文献中都很常用,其实就是![]() 正则化。首先我们注意到联合的先验具有如下的形式:
正则化。首先我们注意到联合的先验具有如下的形式:![]() 。
。
因此我们的对数后验分布具有如下形式(非归一化的):
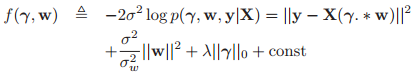
其中:![]() 。
。
同样,我们可以把![]() 分割成两个部分,分别是
分割成两个部分,分别是![]() ,也就是0和非0的两个部分。因此
,也就是0和非0的两个部分。因此![]() 。现在我们考虑
。现在我们考虑![]() ,所以我们不正则化非零权值(这样就没有来自于由于BIC近似或者边缘似然导致的惩罚项)。那么目标就变成:
,所以我们不正则化非零权值(这样就没有来自于由于BIC近似或者边缘似然导致的惩罚项)。那么目标就变成:
![]()
这个和BIC的目标很像。
我们可以不去找比特向量![]() ,而是做如下的处理
,而是做如下的处理![]() ,这个称之为
,这个称之为![]() 正则化,这样,我们就把离散的优化问题转化为离散的优化问题。但是即使是做了这样的改变之后,仍然是不好处理的,因为我们的目标函数仍然是不光滑的,还是很难去优化。
正则化,这样,我们就把离散的优化问题转化为离散的优化问题。但是即使是做了这样的改变之后,仍然是不好处理的,因为我们的目标函数仍然是不光滑的,还是很难去优化。
13.2.3 算法
对于上面的算法,我们计算出了后验或者似然,但是模型的数目依然是![]() ,所以想找一个全局最优解是不可能的。所以,相反我们不得不求助于一些启发式的方法,将这个形式改变成其它的形式。关于每一个方法模型的搜索空间,以及空间里每个点的cost。那我们在每一个固定的模型都要计算最大似然或者是边缘似然即
,所以想找一个全局最优解是不可能的。所以,相反我们不得不求助于一些启发式的方法,将这个形式改变成其它的形式。关于每一个方法模型的搜索空间,以及空间里每个点的cost。那我们在每一个固定的模型都要计算最大似然或者是边缘似然即![]() 或者
或者![]() 。这有时称为包装器方法(wrapper method
。这有时称为包装器方法(wrapper method
),因为我们用一个通用的模型拟合的过程,对一堆模型进行搜索(这个解释自己都觉得怪怪的)。
为了提高包装方法的效率,能够快速的计算新的模型的cost function是很重要的。也就是说对于上一个模型![]() ,对于新的模型
,对于新的模型![]() ,我们能用更新的方法去算,而不是重新计算一边。因为
,我们能用更新的方法去算,而不是重新计算一边。因为![]() 和
和![]() 相比只有一个不同(要不然就是加一项,要不然就是减一项),具体的细节就先不谈,这要根据具体的情况推导。
相比只有一个不同(要不然就是加一项,要不然就是减一项),具体的细节就先不谈,这要根据具体的情况推导。
13.2.3.1 贪婪的搜索
假设我们希望发现MAP模型,如果我们使用![]() 公式,即
公式,即![]() 。我们可以利用最小二乘的性质,推导出各种有效的贪婪搜索方法,我们进行了如下的总结:
。我们可以利用最小二乘的性质,推导出各种有效的贪婪搜索方法,我们进行了如下的总结:
- Single best replacement:在这个方法中,对于
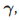 ,我们每一次翻转其中的一个,然后如果比之前的好,就替换掉,比如1000,我们就是先看0000和1000比哪个好,然后再看1100,1010,1001,最后找出这里面的最好的一个,作为新的。因为我们希望找到一个稀疏的解,所以我们一般初始化为
,我们每一次翻转其中的一个,然后如果比之前的好,就替换掉,比如1000,我们就是先看0000和1000比哪个好,然后再看1100,1010,1001,最后找出这里面的最好的一个,作为新的。因为我们希望找到一个稀疏的解,所以我们一般初始化为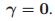 ,就这样不停的做,直到翻转每一个都不会提高性能为止。
,就这样不停的做,直到翻转每一个都不会提高性能为止。 - 正交最小二乘法(Orthogonal least squares):如果我们设定
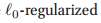 中的
中的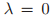 ,那么就没有关于模型复杂度的惩罚项了,那么这个时候我们就没有理由去delete某一项,所以其实在这个情况下,SBR就是正交最小二乘法。在这个算法下,我们同样初始化
,那么就没有关于模型复杂度的惩罚项了,那么这个时候我们就没有理由去delete某一项,所以其实在这个情况下,SBR就是正交最小二乘法。在这个算法下,我们同样初始化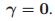 ,在每一步我们都加一项。那么在这个情况下,我们的error肯定是随着
,在每一步我们都加一项。那么在这个情况下,我们的error肯定是随着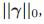 单调下降,如下图:
单调下降,如下图:

我们增加的那一项![]() 必然是
必然是![]() ,然后更新为
,然后更新为![]() 。在这个方法下,我们第t步要计算
。在这个方法下,我们第t步要计算![]() ,其中
,其中![]() 。(我的疑问就是在这个方法中,我们怎么去找稀疏值呢,我们只是看到稀疏值对最终的影响,找拐点?)
。(我的疑问就是在这个方法中,我们怎么去找稀疏值呢,我们只是看到稀疏值对最终的影响,找拐点?)
- 正交匹配追踪(Orthogonal matching pursuits):正交最小二乘法凑从某种程度上说是计算复杂度较高的。所以我们提出一种新的方法,在每一次迭代的时候,我们固定
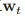 不变,我们通过下面的式子来确定要添加哪一个变量:
不变,我们通过下面的式子来确定要添加哪一个变量:
![]()
其中![]() ,
,![]()
![]() ,这个优化问题更容易解决,因为
,这个优化问题更容易解决,因为![]() 是一个标量。并且如果每一列是单位范数的,我们有:
是一个标量。并且如果每一列是单位范数的,我们有:![]() ,我们可以看到这个式子就是找与当前的残差最接近的那一列。然后我们在利用正交最小二乘里面的式子使用
,我们可以看到这个式子就是找与当前的残差最接近的那一列。然后我们在利用正交最小二乘里面的式子使用![]() 去优化
去优化![]() 。这个方法就叫做正交匹配追踪法(orthogonal matching pursuits,OMP)。在这个方法当中,我们在每一个step只要进行一次最小二乘计算。
。这个方法就叫做正交匹配追踪法(orthogonal matching pursuits,OMP)。在这个方法当中,我们在每一个step只要进行一次最小二乘计算。
- 匹配追踪(matching pursuits):一个更加进攻性的方法,就是不管范数是否为1,直接就是找与残差最相关的那一列,这就是匹配追踪算法。这个方法等价于在16.4.6中讲的least square boosting。
- backwards selection:backwards selection以
开始,然后在每一步中都删除掉最差的那一个。这相当于从格子的顶部向下执行贪婪搜索。这比自底向上的搜索可以得到更好的结果,因为是否保留变量的决策是在可能依赖于它的所有其他变量的上下文中做出的。但是对于大规模的问题,这个方法是不太可行的,因为对于稀疏模型来说,从上往下经历的步数要太多了。
- FoBa:forwards-backwards algorithms跟single best replacement algorithms差不多,但是在进行选择的时候,它使用的是类似于OMP的优化准则(Zhang 2008)。
- 贝叶斯匹配追踪(Bayesian mathching persuit):这个OMP有点像,但是这里使用的是spike and slab模型中的贝叶斯边际似然的函数而不是最小二乘的目标函数。此外,它还使用了一种波束搜索的形式来同时探索通过晶格的多条路径。
13.2.3.2 随机搜索
如果我们希望得到的是后验分布,而不是mode。一个选择就是使用MCMC。标准的方法就是使用Metropolis Hastings(没听过)。这个可以通过![]() 得到
得到![]() ,具体就不去了解了。
,具体就不去了解了。
但是还有一种方法,叫做随机搜索算法,我么用:








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








