机器学习笔记(五)——主成成分分析PCA

主成分分析PCA

介绍

PCA要做的是找到一个方向向量（Vector direction)，当把所有的数据都投射到该向量上时，希望投射平均均方误差能尽可能地小。方向向量是一个经过原点的向量，而投射误差是从特征向量向该方向向量作垂线的长度。

若将$n$维数据降至$k$维，目标是找到向量$u^{(1)}$，$u^{(2)}$，$...,u^{(n)}$，使得总的投射误差最小。

下图中的误差是指：每个点与二维平面上对应投影点之间的距离。

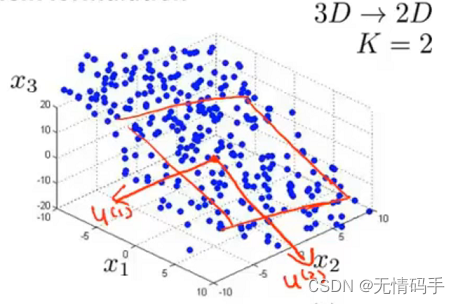
总的来说，PCA是要寻找一个$k$维平面，将原特征(数据)投影到$k$个向量展开的线性子空间上。

算法

1. 均值归一化。计算出所有特征的均值，然后令$x_j=x_j-{\mu }_j$。如果特征是在丕同的数量级上，我们还需要将其除以标准差${\sigma }^2$；
2. 计算协方差矩阵$\Sigma$，$\sum =\frac{1}{m}{\sum }_{i=1}^n\left(x^{(i)}\right){\left(x^{(i)}\right)}^T$（$x^{(i)}\in {\mathbb{R}}^{(n\times 1)}$）;
3. 计算协方差矩阵$\Sigma$的特征向量（可以使用奇异值分解 $[U,S,V]=svd(\Sigma )$）。

$$U=\left[\begin{array}{cccc}\mid & \mid & & \mid \\ u^{(1)}& u^{(2)}& \cdots & u^{(n)}\\ \mid & \mid & & \mid \end{array}\right]\in {\mathbb{R}}^{n\times n}\text{\hspace{1em}(1)}$$

$U$是我们计算得到的特征向量矩阵，我们用$U_{reduce}$来表示它，如果要将原数据由$n$维降为$k$维，需取出$U_{reduce}$矩阵的前$k$列，即前$k$个特征向量。

因此新得到的特征如$(2)$所示，其中，$i$表示它的第$i$维数据。从矩阵规模看，$(k\times 1)=(k\times n)\times (n\times 1)$。对于每行$(1\times n)\times (n\times 1)=1$来说，它表示计算特征向量$u^{(i)}$和$x^{(i)}$的内积，即$x^{(i)}$在特征向量$u^{(i)}$上的投影（之前SVM的笔记中提到过有关内积的介绍，若有疑问可以查阅上一篇笔记）。
$$z^{(i)}=U_{\text{reduce }}^T\ast x^{(i)}\text{\hspace{1em}(2)}$$

$$Z=U_{\text{reduce }}^T\ast X\text{\hspace{1em}(3)}$$

$X\in {\mathbb{R}}^n,Z\in {\mathbb{R}}^k$，从矩阵规模看，$(k\times m)=(k\times n)\times (n\times m)$。

投射误差计算

有些读者可能会有疑问下式是否成立。
$$\begin{array}{rl}{U}_{reduce}Z& =U_{reduce}{U}_{reduce}^{T}X\\ & =EX\\ & =X\end{array}\text{\hspace{1em}(4)}$$
答案是否定的，由于保留的特征数<$m$，因此这个结果不等于$X$，而是产生了误差后的$X_{approx}$。

$$X_{approx}=U_{reduce}Z\text{\hspace{1em}(5)}$$
下图可以清晰地表示出压缩数据过后重建所产生的误差。

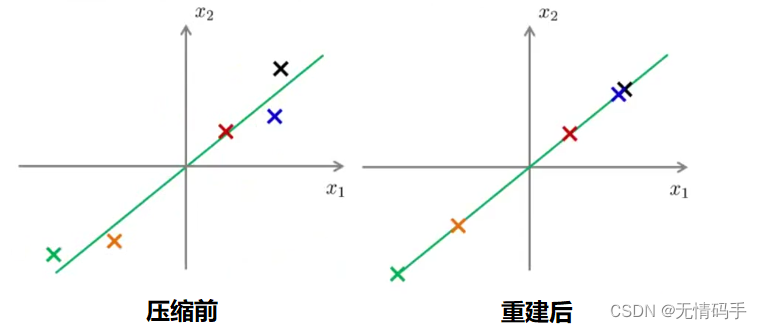
我们可以计算平均均方误差与训练集方差的比例：
$$\frac{\frac{1}{m}{\sum }_{i=1}^m{\Vert x^{(i)}-x_{approx}^{(i)}\Vert }^2}{\frac{1}{m}{\sum }_{i=1}^m{\Vert x^{(i)}\Vert }^2}\text{\hspace{1em}(6)}$$
它还可以表示为(7)式，其中$S$是奇异值分解得到的对角矩阵。
$$1-\frac{{\sum }_{i=1}^k{S}_{ii}}{{\sum }_{i=1}^n{S}_{ii}}\text{\hspace{1em}(7)}$$
我们希望在平均均方误差与训练集方差的比例尽可能小的情况下选择尽可能小的k值。如果我们希望这个比例小于1%，就意味着原本数据的偏差有99%都保留下来了，如果我们选择保留95%的偏差，便能非常显著地降低模型中特征的维度了。

易错点

1. $U_{reduce}$是在训练集上学习得到的，而非测试集和交叉验证集。对于测试集和交叉验证集，他们用的也是训练集上学习得到的$U_{reduce}$；
2. 将PCA用于减少过拟合（减少了特征的数量)。这样做非常不好，不如尝试正则化处理。原因在于PCA只是近似地丢弃掉一些特征，它并不考虑任何与结果变量有关的信息，因此可能会丢失非常重要的特征。然而当我们进行正则化处理时，会考虑到结果变量，不会丢掉重要的数据；
3. 默认地将PCA作为学习过程的一部分。最好还是使用所有原始特征，当有需要时再使用PCA。

代码

任务一：二维数据降为成一维

加载数据并显示

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat

data = loadmat('data/ex7data1.mat')
print(data)
X = data['X']
print(X.shape)

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(X[:, 0], X[:, 1])
plt.show()

定义PCA

#PCA的算法相当简单。 在确保数据被归一化之后，输出仅仅是原始数据的协方差矩阵的奇异值分解。
def pca(X):
    # normalize the features
    X = (X - X.mean()) / X.std()

    # compute the covariance matrix
    X = np.matrix(X)
    cov = (X.T * X) / X.shape[0]

    # perform SVD
    U, S, V = np.linalg.svd(cov)

    return U, S, V

U, S, V = pca(X)
def project_data(X, U, k):
    U_reduced = U[:,:k]
    #这里X是行向量，所以是X*U_r (m,n) * (n,k) -> (m,k)
    return np.dot(X, U_reduced)

执行并重建

#将原始数据投影到一个较低维的空间中
Z = project_data(X, U, 1)
print(Z)

#反向恢复原始数据
def recover_data(Z, U, k):
    U_reduced = U[:,:k]
    return np.dot(Z, U_reduced.T)

X_recovered = recover_data(Z, U, 1)
print(X_recovered)

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(list(X_recovered[:, 0]), list(X_recovered[:, 1]))
plt.show()

任务二：通过使用相同的降维技术将PCA应用于脸部图像

加载数据

faces = loadmat('data/ex7faces.mat')
X = faces['X']
print(X.shape)

face = np.reshape(X[3,:], (32, 32))
plt.imshow(face)
plt.show()

执行并重建

#执行PCA
U, S, V = pca(X)
Z = project_data(X, U, 100)

#恢复重建展示
X_recovered = recover_data(Z, U, 100)
face = np.reshape(X_recovered[3,:], (32, 32))
plt.imshow(face)
plt.show()