PCA入门级理解

深度学习系列

第一篇 局部最优点+鞍点+学习率的调节
第二篇 并行计算 深度学习 机器学习
第三篇 长短期记忆网络（LSTM）是什么怎么工作的呢？
第四篇 Dropout解析 代码实现
第五篇 Auto-encoder 自编码器
第六篇 ResNet,Xception,DenseNet优缺点对比
第六篇 STM网络（Spatial Transformer Network）常见疑问解答
第七篇 Self-attention入门级详解
第八篇 PCA入门级理解

---

---

前言

我们都知道PCA的作用是用于数据降维，但是繁杂的数学公式很容易劝退我们。但是PCA最终问题会转化为一个数学问题，具体为线性代数和概率论的问题，所以数学是避免不了的。所以，如果没学过线性代数和概率论的伙伴看起来可能会有点吃力。

但是我会尽量以通俗易懂的方式讲解！

---

一、前置概念

1.方差

方差是数据离散程度的度量

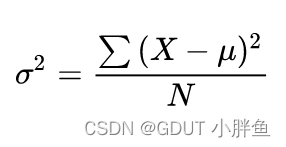
μ为为整体样本的均值

但是我们会看到有的方差分母为n-1，那个是样本方差。

1.1为什么要用n-1？

这里提一嘴。
样本方差的出现是因为有时候计算方差需要算整体的平均值，但是我们不一定能得到整体均值，所以我们使用样本方差进行估计。所以我们进行抽样，比如(X1,X2,X3,X4,X5,X6)，我们抽取6个元素，但是抽取过程中，大部分数据会从整体数据中数据集中的地方抽取过来（比如在学校中对人群抽样，抽到的肯定大部分是学生，而不是老师），但是我们不能忽略出现概率低的数据，但是由于我们是抽样，所以总是会有一定的偏差。大部分的数据是集中在出现概率高的范围内，所以离散度小，即方差小，我们会低估了方差，所以我们把n换成n-1,以此来提高方差，进行修正，所以样本方差会有人说他说总体方差的无偏估计。

至于为什么是n-1，不是n-2或者n-3， 这里是有数学证明的，我从小崔老师那拿来，有兴趣的可以看一下。

2.协方差

协方差是作用是表示两个变量的相关程度。但是协方差也有总体协方差和样本协方差，在PCA中使用的是样本协方差。

总体协方差公式：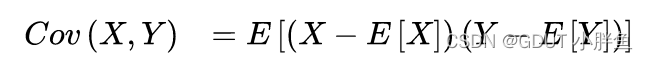
样本协方差公式:
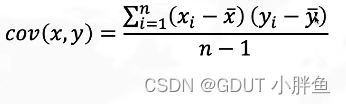有不理解的伙伴，可以先看这个视频，立马就懂：
如何通俗地解释协方差

有的人会有疑问，为什么一个公式里面有期望，一个里面是n-1
因为，这就是总体协方差和样本协方差的区别。总体协方差中的期望其实就是加权的平均值（不知道为什么请看视频），而样本协方差中只是估计量而已，也不知道整体概率。所以可能还是会有偏差，这也就是为什么人们会对数据进行预处理，进行标准化，归一化等处理。

当x增大，y也增大 则协方差>0，正相关
当x增大，y可能增大，也可能减小，则不相关
当x增大，y减小，则负相关

3.协方差矩阵

协方差矩阵是在把PCA问题转化为数学问题中使用的。其形式如下：
![协方差矩阵](https://img-blog.csdnimg.cn/0d9b20ec76924e1885f30c33e6c65675.png
正对角线为方差，负对角线为协方差。（在PCA中会先对数据去中心化，所以均值为0，所以协方差的写法就变成上面负对角线的样子）
他的意义在于写成这种形式方便解决数学问题
因为协方差矩阵与我们的数据有着相乘的关系，协方差矩阵可表示如下

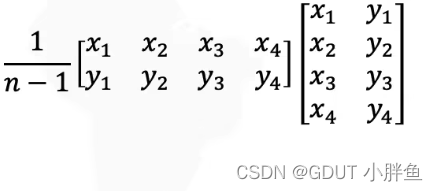
二、PCA讲解

PCA的第一步是去中心化，表现在图上就是数据的中心移动到原点，他的作用就是让均值为0，方便计算。

PCA是为了数据降维，例如，对于一个二维平面，我们就是找一条线，将这些平面的点投影到线上。对于三维的立体空间，我们降到二维，即找一个平面，把空间中的点压缩到平面上。下面是一个二维降维到一维的例子。

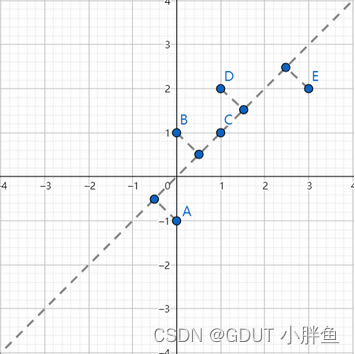
但是我们立马会发现一个问题，如果有两个二维的点降维到一维的时候，不就重复了？

是的，这就是降维造成的损失。所以，我们任务就是去找一个这种损失最小的一维线。

要使得损失最小，那么就需要离散度最大，数据分散得开，不会集中在一起，肯定重复的就少，即方差最大！这是我们的第一个条件！

---

那当我们要从三维降到二维的时候，我们需要找两个一维的线，我们希望这两个一维的线是无关的，即协方差为0。**** 这是我们第二个条件！

为什么需要无关呢？
举个例子，如果我们有出生日期和年龄这个数据，就会发现从一个出生日期已近能推出年龄了，它们是有相关性的，而我们是要做主成分分析，不希望有这种冗余，所以让表示相关性的协方差为0，即无关。

---

这时候就可以拿出我们的协方差矩阵了！
现在有两个条件，一个为方差最大，一个为协方差=0。在协方差矩阵上的表示为对角线最大，负对角线为0。所以我们现在把问题转化为协方差矩阵对角化的问题。

协方差矩阵C是一个是对称矩阵，在线性代数上，实对称矩阵有以下的性质：

1.实对称矩阵不同特征值对应的特征向量必然正交。
2.设特征向量λ重数为r，则必然存在r个线性无关的特征向量对应于λ，因此可以将这r个特征向量单位正交化。

如果没学过线性代数，可能觉得这里比较不懂，这个对角化的过程是线性代数里面的一个重点，对角化后，一个特征向量对应一个特征值，其他向量都可以用这些特征向量去表示

我们继续。
例如，我们最后n个特征向量为e1,e2,⋯,en，我们将其排列成E = (e1 e2 ⋯ en)，那么对角化后就为：

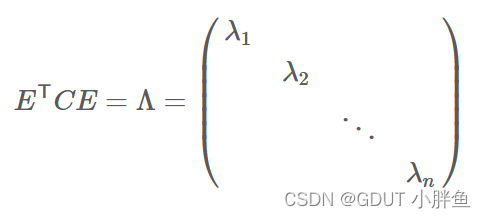
到此，我们得到我们想要的矩阵E，它里面有多个特征向量，每个特征向量代表一个维度。我们将特征值按大小排列，比如要用2维表示，那么就选取最大前两个特征值对应的特征向量，想要3维也类似。

具体要几维呢？

这里说明一下，特征值是协方差矩阵的特征向量对应的标量，它表示了在这个方向上数据的方差**（对角化协方差=0，但是维度方向不同方差的大小也不同，可以选取大的）**。而PCA的目标就是找到数据的主要方向，也就是方差最大的方向。因此，特征值越大，说明这个方向上的方差越大，对应的特征向量就是数据集中的主要方向。

这里引入一个概念，碎石图，即方差（特征值）在所有方差（特征值）的占比，如下图，如果我们使用前前两个维度已近能够表示大部分的信息，那就使用二维，不需要三维。

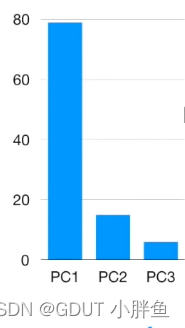
最后我们选取了需要的特征值，例如选取了最大两个，我们找到它们的特征向量，将特征向量和原始数据进行矩阵相乘（矩阵相乘的意义就是空间变化）。

下面这篇文章最后面有个例子，可以看一下
PCA的数学原理

四、Reference

[1]主成分分析（PCA）原理详解

---

总结

以上就是我个人对PCA主成分分析的理解，希望配合上其他文章，能让初学者更容易理解。如果觉得有用，请大家点赞支持！！！！。