ScSPM和LLC

 

图像的稀疏表示——ScSPM和LLC的总结

分类： Machine Learning 2013-08-09 09:52  790人阅读  评论(5)  收藏  举报

Sparse Representatio 稀疏编码

目录(?)[+]

稀疏编码系列：

• （一）----Spatial Pyramid 小结
• （二）----图像的稀疏表示——ScSPM和LLC的总结
• （三）----理解sparse coding
• （四）----稀疏模型与结构性稀疏模型

---------------------------------------------------------------------------

 

• 前言

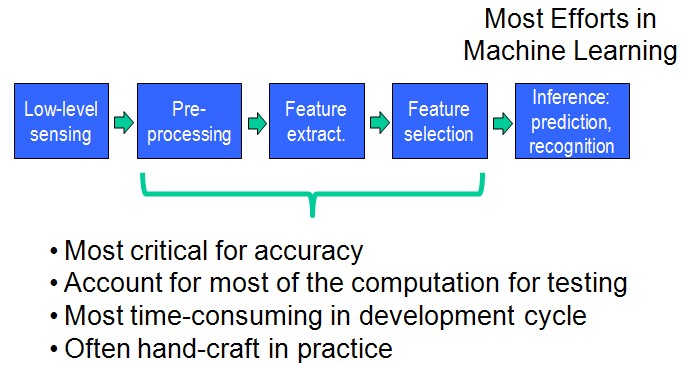
       上一篇提到了SPM。这篇博客打算把ScSPM和LLC一起总结了。ScSPM和LLC其实都是对SPM的改进。这些技术，都是对特征的描述。它们既没有创造出新的特征（都是提取SIFT,HOG, RGB-histogram et al），也没有用新的分类器（也都用SVM用于最后的image classification），重点都在于如何由SIFT、HOG形成图像的特征（见图1）。从BOW，到BOW+SPM，都是在做这一步。说到这，怕会迷糊大家------SIFT、HOG本身不就是提取出的特征么，它们不就已经形成了对图像的描述了吗，为啥还有我后面提到的各种BOW云云呢。这个问题没错，SIFT和HOG它们确实本身已经是提取到的特征了，我们姑且把它们记为x。而现在，BOW+SPM是对特征x再进行一层描述，就成了Φ(x)——这相当于是更深一层（deeper）的model。一个十分相似的概念是SVM里面的核函数kernel，K=Φ(x)Φ(x)，x是输入的特征，Φ(x)则对输入的特征又做了一层抽象（不过我们用核函数没有显式地对Φ(x)做定义罢了）。根据百度的余凯老师在CVPR2012的那个Tutorial上做的总结[5]：Deeper model is preferred，自然做深一层的抽象效果会更好了。而Deep Learning也是同样的道理变得火了起来。

       再次盗用一些余凯老师在CVPR2012的那个Tutorial上的一些图：

图 （1）

        SPM，ScSPM，LLC所做的工作也都集中在design feature这一步，而不是在Machine Learning那一步。值得注意的是，我们一直在Design features，而deep learning则是design feature learners。

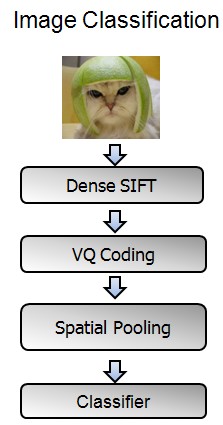
      BOW+SPM的整体流程如图(2)所示：

图（2）

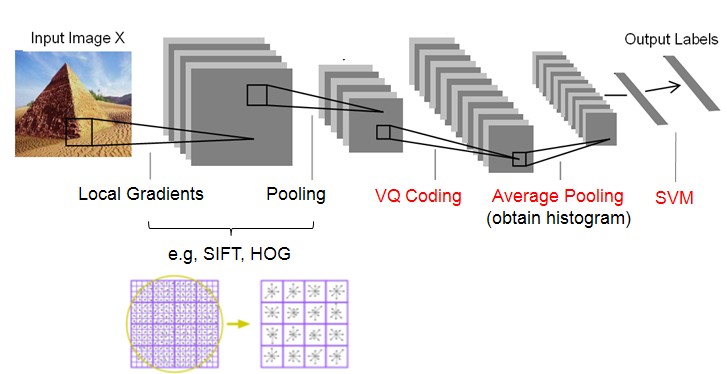
        Feature Extraction的整体过程就是先提取底层的特征（SIFT，HOG等），然后经过coding和pooling，得到最后的特征表示。

             ----Coding: nonlinear mapping data into another feature space

             ----Pooling: obtain histogram

        而SIFT、HOG本身就是一个coding+pooling的过程，因此BOW+SPM就是一个两层的Coding+Pooling的过程。所以可以说，SIFT、SURF等特征的提出，是为了寻找更好的第一层Coding+Pooling的办法；而SPM、ScSPM、LLC的提出，是为了寻找更好的第二层Coding+Pooling的办法。而ScSPM和LLC所提出的更好的Coding办法就是Sparse Coding。

图（3）

 

• 再前言

        在总结ScSPM之前又要啰嗦些话。为啥会有SPM→ScSPM呢？原因之一是为了寻找better coding + better pooling的方式提高性能，原因之二就是提高速度。如何提高速度？这里的速度，不是Coding+Pooling的速度，而是分类器的速度。SPM设计的是一个Linear feature，在文章中作者用于实验则是用了nonlinear SVM（要用Mercer Kernels）。相比linear SVM，nonlinear SVM在training和testing的时候速度会慢的。至于其原因，我们不妨看看SVM的对偶形式：

(1)

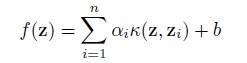
        如果核函数是一个线性的kernel：K(z, z_i)=z^Tz_i，那么SVM的决策函数就可以改写为：

    (2)

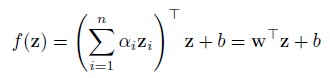
          从两式可以看见，抛开训练和存储的复杂度不说，对于测试来说，（1）式对每个测试样本要单独计算K(z, z_i)，因此testing的时间复杂度为O(n)。而（2）式的w^T可以一次性事先算出，所以每次testing的时间复杂度为O(1)。此外，linear classifier的可扩展性会更好。

          因此，如果能在coding+pooling后设计得到线性可分的特征描述，那就最好了。因此能否设计一个nonlinear feature + linear SVM得到与 linear feature + nonlinear SVM等效甚至更好的效果，成为ScSPM和LLC的研究重点。

• ScSPM

        SPM在coding一步采用的是Hard-VQ，也就是说一个descriptor只能投影到dictionary中的一个term上。这样就造成了明显的重建误差（worse reconstruction，large quantization errors）。这样，原本很相似的descripors经过coding之后就会变得非常不相似了。ScSPM为此取消了这一约束，它认为descripor可以投影到某几个terms上，而不仅仅是一个。因此，其目标函数变成了：

     (3)

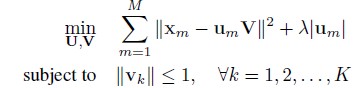
        其中M是descriptor的数目，Um表示第m个descriptor在字典V上的投影系数。

        它对投影系数用L1-norm做约束实现了稀疏。求解问题称为LASSO (least absolute shrinkage and selection operator)，在得到稀疏结果的同时，它无法得到解析解，因此速度肯定是很慢的。关于L1-norm和LASSO问题，可以参看这里。

        为什么Sparse Coding好，主要有以下几个原因：

      1）已经提到过的重建性能好；[2]

      2）sparse有助于获取salient patterns of descripors；[2]

      3）image statistics方面的研究表明image patches都是sparse signals；[2]

      4）biological visual systems的研究表明信号的稀疏特征有助于学习；[4]

      5）稀疏的特征更加线性可分。[2]

         总之，"Sparse coding is a better building block“。

         Coding过后，ScSPM采用的Pooling方法是max pooling：Z_j=max U_ij。相比SPM的average pooling：Z_j=1/M *Σ U_ij。可以看见average pooling是一个linear feature representation，而max pooling是nonlinear的。我是这么理解再前言中提到的linear和nonlinear feature的。(@13.08.11:今天在写理解sparse coding的时候发现这里搞错了。不光是pooling的函数是线性的，VQ的coding得到的u关于x好像也是线性的。)

        作者在实验中得出max pooling的效果好于average pooling，原因是max pooling对local spatial variations比较鲁棒。而Hard-VQ就不好用max pooling了，因为U中各元素非0即1。

        另外实验的一个有趣结果是发现ScSPM对大的codebook size表现出更好的性能，反观SPM，codebook大小对SPM结果影响不大。至于为啥，我也不懂。

• LLC

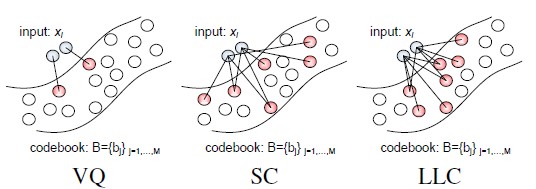
         LLC和ScSPM差不多了，也是利用了Sparsity。值得一说的是，其实Hard-VQ也是一种Sparse Coding，只不过它是一种重建误差比较大的稀疏编码。LLC对ScSPM的改进，则在于引入了locality。为了便于描述，盗用一下论文的图：

图（4）

        这个图实在是太棒了，太能解释问题了。VQ不用说，重点在于SC和LLC之间，LLC引入了locality的约束，即不仅仅是sparse要满足，非零的系数还应该赋值给相近的dictionary terms。作者在[4]中解释到，locality 很重要是因为：

     1）nonlinear function的一阶近似要求codes是local的；

     2）locality能够保证codes的稀疏性，而稀疏却不能保证locality；

     3）稀疏的coding只有再codes有局部性的时候有助于learning。

        总之，"locality is more essential than sparsity"。

        LLC的目标函数是：

     (4)

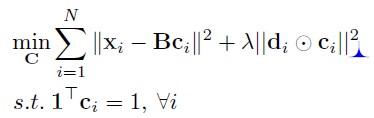
       和（3）一样，（4）可以按照加号的前后分成两部分：加号前的一项最小化是为了减少量化误差（学习字典、确认投影系数）；加号后的一项则是做出假设约束（包括是一些参数的regularization）。这个求解是可以得到闭合解的，同时也有快速的近似算法解决这个问题，因此速度上比ScSPM快。

       di描述的是xi到每个dictionary term的距离。显然这么做是为了降低距离大的term对应的系数。

       locality体现出的最大优势就是，相似的descriptors之间可以共享相似的descriptors，因此保留了codes之间的correlation。而SC为了最小化重建误差，可能引入了不相邻的terms，所以不能保证smooth。Hard-VQ则更不用说了。

       实验部分，则采用max pooling + L2-normalization。

   

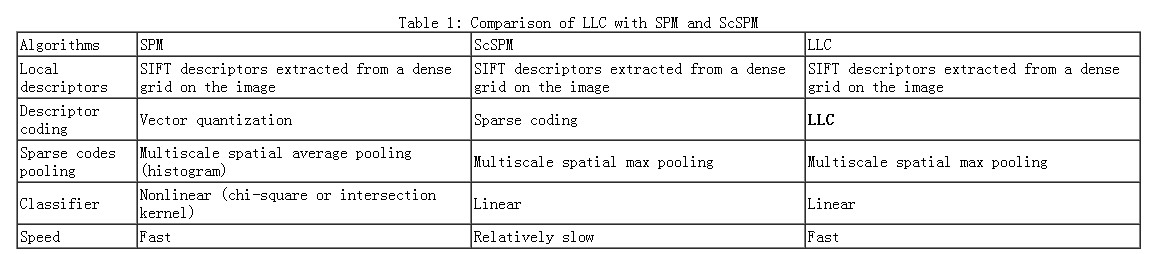
        文章的最后，盗窃一个ScSPM第一作者的总结表格结束吧（又是以偷窃别人图标的方式结束）

 

References：

[1] S. Lazebnik, C. Schmid, and J. Ponce. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. CVPR2006

[2] Jianchao Yang, Kai Yu, Yihong Gong, and Thomas Huang. Linear spatial pyramid matching using sparse coding for image classification. CVPR2009.

[3] Jinjun Wang, Jianchao Yang, Kai Yu, Fengjun Lv, and Thomas Huang. Locality-constrained linear coding for image classification. CVPR2010

[4] Kai Yu, Tong Zhang, and Yihong Gong. Nonlinear learning using local coordinate coding. NIPS2009.

[5] Kai Yu. CVPR12 Tutorial on Deep Learning: Sparse Coding.

-----------------------

作者：jiang1st2010

引用请注明来源：http://blog.csdn.net/jwh_bupt/article/details/9837555