Riemann问题精确解及程序实现

学习自李新亮的《计算流体力学讲义PPT》第2讲 双曲型方程组及间断解

1 问题描述

一维无粘流动初始间断的演化问题，激波管问题（Sod激波管问题），由于该问题属于典型的间断问题，且有精确解存在，故广泛用于对比验证CFD中离散格式、数值方法的准确性，意义嘛还是蛮重要的，哈。

一无限长管道内部充满理想气体（无粘），中间有一不计厚度的隔膜，初始时刻$t_0$，左侧气体的速度、密度、压力分别为$u_1$、${\rho }_1$、$p_1$，右侧气体的速度、密度、压力分别为$u_2$、${\rho }_2$、$p_2$。不考虑流体粘性，突然将隔膜抽出（也可认为隔膜突然消失），那么到时刻$t$后，管道内流体的速度、密度、压力将如何分布？

---------------------------------------------------------
　　$u_1,{\rho }_1,p_1$ 　　 | 　　$u_2,{\rho }_2,p_2$
---------------------------------------------------------

控制方程为一维Euler方程（即无粘可压缩理想流体一维流动的控制方程）：
$$\{\begin{array}{l}\frac{\partial \rho }{\partial t}+\frac{\partial (\rho u)}{\partial x}=0\\ \\ \frac{\partial (\rho u)}{\partial t}+\frac{\partial (\rho u^2+p)}{\partial x}=0\\ \\ \frac{\partial (\rho E)}{\partial t}+\frac{\partial (\rho Eu+pu)}{\partial x}=0\end{array}$$

初始条件：

$$t=t_0时,(u,\rho ,p)=\{\begin{array}{ll}{u}_1,{\rho }_1,p_1& x<0\\ u_2,{\rho }_2,p_2& x\ge 0\end{array}$$

另外，求解方程需要用到的变量为理想气体比热比$\gamma =1.4$，气体守恒能量$\rho E$与气体其他状态参数的关系式

$$\rho E=\frac{p}{\gamma -1}+\rho \frac{u^2}{2}$$

声速与气体其他状态参数的关系式

$$c=\sqrt{\gamma \frac{p}{\rho }}$$

2 求解方法

流场中可能出现三种波：

间断类型	特征
激波	强间断，满足R-H关系式
接触间断	特殊间断，仅密度突变，而速度和压力不变
膨胀波	等熵波

依据不同的初始条件，可以产生五类不同的情况，分别为
（1）左激波-接触间断-右激波
（2）左膨胀波-接触间断-右激波
（3）左激波-接触间断-右膨胀波
（4）左膨胀波-接触间断-右膨胀波
（5）左膨胀波-右膨胀波

2.1 情况1，左右激波和中间的接触间断

区域1和区域2中物理量与初始状态一致，分别为$u_1$、${\rho }_1$、$p_1$和$u_2$、${\rho }_2$、$p_2$；

待求量为左激波运动速度$Z_1$、右激波运动速度$Z_2$，注意左激波是向左运动的，右激波是向右运动的，这里把$Z_1$和$Z_2$的正方向都定义为沿着$x$轴的正方向。

区域3和区域4中物理量也为待求量，由于接触间断两侧仅密度产生突变，故区域3和区域4中的速度和压力时相同的，将其定义为$u^{\ast }$和$p^{\ast }$，将区域3和区域4的密度分别定义为${\rho }^{\ast L}$和${\rho }^{\ast R}$。注意，中间接触间断面的运动速度并不是未知量，因为该间断面两侧速度相同，都为$u^{\ast }$，所以该间断面的运动速度也为$u^{\ast }$。

那么总共有6个未知量，即$Z_1$、$Z_2$、$u^{\ast }$、$p^{\ast }$、${\rho }^{\ast L}$和${\rho }^{\ast R}$。

在激波两侧的物理量满足R-H关系，即质量、动量、能量通量守恒，即

$$\{\begin{array}{l}{\rho }_1(u_1-Z)={\rho }_2(u_2-Z)\\ {\rho }_1{u}_1(u_1-Z)+p_1={\rho }_2{u}_2(u_2-Z)+p_2\\ {\rho }_1{E}_1(u_1-Z)+u_1{p}_1={\rho }_2{E}_2(u_2-Z)+u_2{p}_2\end{array}$$

那么，对于1-3两区
$$\{\begin{array}{ll}{\rho }_1(u_1-Z_1)={\rho }^{\ast L}(u^{\ast }-Z_1)& (1)\\ {\rho }_1{u}_1(u_1-Z_1)+p_1={\rho }^{\ast L}{u}^{\ast }(u^{\ast }-Z_1)+p^{\ast }& (2)\\ {\rho }_1{E}_1(u_1-Z_1)+u_1{p}_1={\rho }^{\ast L}{E}^{\ast L}(u^{\ast }-Z_1)+u^{\ast }{p}^{\ast }& (3)\end{array}$$

对于2-4两区
$$\{\begin{array}{ll}{\rho }_2(u_2-Z_2)={\rho }^{\ast R}(u^{\ast }-Z_2)& (4)\\ {\rho }_2{u}_2(u_2-Z_2)+p_2={\rho }^{\ast R}{u}^{\ast }(u^{\ast }-Z_2)+p^{\ast }& (5)\\ {\rho }_2{E}_2(u_2-Z_2)+u_2{p}_2={\rho }^{\ast R}{E}^{\ast R}(u^{\ast }-Z_2)+u^{\ast }{p}^{\ast }& (6)\end{array}$$

总共6个方程(1)-(6)，6个未知数，可解。

解法如下：

先来看1-3区的关系式(1)-(3)，共有4个未知数${\rho }^{\ast L}$、$u^{\ast }$、$Z_1$、$p^{\ast }$，注意$E^{\ast L}$是其他状态参数的函数，不属于未知量，其与其他量关系为：

$${\rho }^{\ast L}{E}^{\ast L}=\frac{p^{\ast }}{\gamma -1}+{\rho }^{\ast L}\frac{(u^{\ast }{)}^2}{2}(7)$$

接下来要做的是从(1)-(3)中消去${\rho }^{\ast L}$和$Z_1$，找到$u^{\ast }$和$p^{\ast }$的关系式，先由(1)可得
$${\rho }^{\ast L}=\frac{{\rho }_1(u_1-Z_1)}{(u^{\ast }-Z_1)}(8)$$

将上式(8)代入到式(2)，消去${\rho }^{\ast L}$，可得
$${\rho }_1(u_1-Z_1)(u_1-u^{\ast })=p^{\ast }-p_1(9)$$

将式(8)代入式(3)，消去${\rho }^{\ast L}$，并将能量$E_1$和$E^{\ast L}$用压力、密度和速度来表示，可得
$$\left(\frac{p_1}{\gamma -1}+{\rho }_1\frac{u_1^2}{2}\right)(u_1-Z_1)+u_1{p}_1=\frac{p^{\ast }}{\gamma -1}(u^{\ast }-Z_1)+{\rho }_1\frac{(u^{\ast }{)}^2}{2}(u_1-Z_1)+u^{\ast }{p}^{\ast }$$

即
$$\left[\frac{p_1}{\gamma -1}+{\rho }_1\frac{u_1^2-(u^{\ast }{)}^2}{2}\right](u_1-Z_1)=\frac{p^{\ast }}{\gamma -1}(u^{\ast }-Z_1)+u^{\ast }{p}^{\ast }-u_1{p}_1(10)$$

相当于把原本的式(2)和式(3)消去了${\rho }^{\ast L}$，转化为了式(9)和式(10)，接下来想办法从式(9)和式(10)中消去$Z_1$，由式(9)可得
$$Z_1=u_1-\frac{p^{\ast }-p_1}{{\rho }_1(u_1-u^{\ast })}(11)$$

将上式代入到式(10)中，得到
$$\left[\frac{p_1}{\gamma -1}+{\rho }_1\frac{u_1^2-(u^{\ast }{)}^2}{2}\right]\frac{p^{\ast }-p_1}{{\rho }_1(u_1-u^{\ast })}=\frac{p^{\ast }}{\gamma -1}\left[u^{\ast }-u_1+\frac{p^{\ast }-p_1}{{\rho }_1(u_1-u^{\ast })}\right]+u^{\ast }{p}^{\ast }-u_1{p}_1$$

即
$$\frac{p_1-p^{\ast }}{\gamma -1}\frac{p^{\ast }-p_1}{{\rho }_1(u_1-u^{\ast })}+\frac{1}{2}(p^{\ast }-p_1)(u_1+u^{\ast })=\frac{\gamma p^{\ast }}{\gamma -1}(u^{\ast }-u_1)+u_1(p^{\ast }-p_1)$$

即
$$\frac{(p_1-p^{\ast }{)}^2}{{\rho }_1(\gamma -1)(u^{\ast }-u_1)}+\frac{1}{2}(p^{\ast }-p_1)(u^{\ast }-u_1)=\frac{\gamma p^{\ast }}{\gamma -1}(u^{\ast }-u_1)$$

即
$$\frac{(p_1-p^{\ast }{)}^2}{{\rho }_1(\gamma -1)(u^{\ast }-u_1)}=\frac{(\gamma +1)p^{\ast }+(\gamma -1)p_1}{2(\gamma -1)}(u^{\ast }-u_1)$$

即
$$\frac{2(p_1-p^{\ast }{)}^2}{(\gamma +1)p^{\ast }+(\gamma -1)p_1}={\rho }_1(u^{\ast }-u_1{)}^2$$

即
$$|u^{\ast }-u_1|=|p_1-p^{\ast }|\sqrt{\frac{2}{{\rho }_1[(\gamma +1)p^{\ast }+(\gamma -1)p_1]}}$$

这时候需要考虑$p_1-p^{\ast }$，$u^{\ast }-u_1$的正负问题，由于是左行激波，激波运动速度$Z_1<0$，那么根据式(11)有
$$Z_1=u_1-\frac{p^{\ast }-p_1}{{\rho }_1(u_1-u^{\ast })}<0$$

即
$$u_1<\frac{p^{\ast }-p_1}{{\rho }_1(u_1-u^{\ast })}$$

毫无疑问，密度必须是正值${\rho }_1>0$，而激波后部压力要大于前面，即有$p^{\ast }>p_1$。
若$u_1\ge 0$，则$p^{\ast }-p_1$与$u_1-u^{\ast }$同号，才能保证$RHS\ge 0$；
若$u_1<0$，则$p^{\ast }-p_1$与$u_1-u^{\ast }$同号时，能保证$RHS>0>u_1$，而$p^{\ast }-p_1$与$u_1-u^{\ast }$异号时，应该不会出现这种情况，具体怎么个分析解释，我暂时也没弄明白，汗颜……。
不论如何，这里经过分析，可以得到，左行激波的$p^{\ast }>p_1$，而$u_1>u^{\ast }$。

故可推得$u^{\ast }$与$p^{\ast }$的关系式
$$u^{\ast }=u_1+(p_1-p^{\ast })\sqrt{\frac{2}{{\rho }_1[(\gamma +1)p^{\ast }+(\gamma -1)p_1]}}$$

一般写成如下形式：
$$u^{\ast }=u_1-\frac{p^{\ast }-p_1}{{\rho }_1{c}_1\sqrt{\frac{\gamma +1}{2\gamma }\frac{p^{\ast }}{p_1}+\frac{\gamma -1}{2\gamma }}}=u_1-f(p^{\ast },p_1,{\rho }_1)(12)$$

其中声速$c_1=\sqrt{\gamma p_1/{\rho }_1}$

采用同样的方法，也可以从2-4区的关系式(4)-(6)推出$u^{\ast }$与$p^{\ast }$、$u_2$、${\rho }_2$、$p_2$的关系式，注意，由于是右行激波，分析后发现$p^{\ast }>p_2$，而$u_2<u^{\ast }$，所以式子里面是加号：
$$u^{\ast }=u_2+\frac{p^{\ast }-p_2}{{\rho }_2{c}_2\sqrt{\frac{\gamma +1}{2\gamma }\frac{p^{\ast }}{p_2}+\frac{\gamma -1}{2\gamma }}}=u_2+f(p^{\ast },p_2,{\rho }_2)(13)$$

其中声速$c_2=\sqrt{\gamma p_2/{\rho }_2}$
综合考虑式(12)和式(13)，他俩的右端项是相等的，可以消去$u^{\ast }$，得到关于$p^{\ast }$的方程，如下：
$$u_1-u_2=f(p^{\ast },p_1,{\rho }_1)+f(p^{\ast },p_2,{\rho }_2)\equiv F(p^{\ast })(14)$$

上式中仅含一个未知量$p^{\ast }$，所以可解，然而方程本身非线性，所以没有解析形式的解，好在$F(p^{\ast })$函数自身具有很好的单调性，为单调增函数，所以对于给定的$p_1$、$p_2$、$u_1$、$u_2$、${\rho }_1$、${\rho }_2$，可以很方便地用二分法或Newton法来获得数值解$p^{\ast }$。

算得$p^{\ast }$之后，可以先用式(12)或式(13)来算出$u^{\ast }$，再由式(11)来算出$Z_1$（$Z_2$的算法是一样的），最后用式(8)算出${\rho }^{\ast L}$（${\rho }^{\ast R}$的算法是一样的）。

至此，已经获取了情况1的全部6个未知量，即$Z_1$、$Z_2$、$u^{\ast }$、$p^{\ast }$、${\rho }^{\ast L}$和${\rho }^{\ast R}$。

2.2 情况2，左膨胀波，右激波，中间接触间断

$(u_1,p_1,{\rho }_1)=(0,1,1),(u_2,p_2,{\rho }_2)=(0,0.1,0.125)$的初始状态，在t=0.14s的参数如下，这属于情况2。

咱们先计算(3)和(4)两区的值，再计算膨胀波内部(5)区的值。

2-4两区仍然满足R-H关系，与情况1完全一样：
$$\{\begin{array}{ll}{\rho }_2(u_2-Z_2)={\rho }^{\ast R}(u^{\ast }-Z_2)& (15)\\ {\rho }_2{u}_2(u_2-Z_2)+p_2={\rho }^{\ast R}{u}^{\ast }(u^{\ast }-Z_2)+p^{\ast }& (16)\\ {\rho }_2{E}_2(u_2-Z_2)+u_2{p}_2={\rho }^{\ast R}{E}^{\ast R}(u^{\ast }-Z_2)+u^{\ast }{p}^{\ast }& (17)\end{array}$$

1-3两区，首先要满足等熵关系，其次要满足Riemann不变量的相等，即
$$\{\begin{array}{ll}\frac{p^{\ast }}{({\rho }^{\ast L}{)}^{\gamma }}=\frac{p_1}{({\rho }_1{)}^{\gamma }}& (18)\\ & \\ u_1+\frac{2c_1}{\gamma -1}=u^{\ast }+\frac{2c^L}{\gamma -1}& (19)\end{array}$$

其中$c_1=\sqrt{\gamma p_1/{\rho }_1}$，$c^L=\sqrt{\gamma p^{\ast }/{\rho }^{\ast L}}$

关于Riemann不变量，实际上是由1维Euler方程做特征分析所推导出来的，即有两个特征线$dx/dt=u+c$和$dx/dt=u-c$，在这俩特征线上Riemann量$R_1$和$R_2$保持不变，即
$$\{\begin{array}{llccc}{R}_1=u+\frac{2c}{\gamma -1}=const& & & & at\frac{dx}{dt}=u+c\\ & & & & \\ R_2=u-\frac{2c}{\gamma -1}=const& & & & at\frac{dx}{dt}=u-c\end{array}$$

对于情况1而言，这里蓝色是特征线1，向右传播，红色是特征线2，向左传播。那么，在蓝线上（显然在时空图上，它可以从1区穿过5区穿过3区），都有$R_1为常数$，故而，有式(19)存在。

式(15)-(19)共5个方程，5个未知数$Z_2$、$u^{\ast }$、$p^{\ast }$、${\rho }^{\ast L}$和${\rho }^{\ast R}$，比情况1少了个$Z_1$，可解。

由式(18)(19)可以推导出，$u^{\ast }$和$p^{\ast }$的关系：
$$u^{\ast }=u_1-\frac{2c_1}{\gamma -1}\left[{\left(\frac{p^{\ast }}{p_1}\right)}^{\frac{\gamma -1}{2\gamma }}-1\right]=u_1-f(p^{\ast },p_1,{\rho }_1)(20)$$

与情况1一样的，从2-4两区关系式中可以推出$u^{\ast }$和$p^{\ast }$的关系式(13)，将其与上式结合起来，便可消去$u^{\ast }$，得到仅包含未知量$p^{\ast }$的方程，同样可以采用数值方法来求出$p^{\ast }$。

为方便计，可以将激波和膨胀波的速度压力关系写成统一的表达形式：

左波（激波或膨胀波）$u^{\ast }=u_1-f(p^{\ast },p_1,{\rho }_1)$

右波（激波或膨胀波）$u^{\ast }=u_2+f(p^{\ast },p_2,{\rho }_2)$

其中，函数$f(p^{\ast },p_i,{\rho }_i)$为：
$$f(p^{\ast },p_i,{\rho }_i)=\{\begin{array}{llccc}\frac{p^{\ast }-p_i}{{\rho }_i{c}_i\sqrt{\frac{\gamma +1}{2\gamma }\frac{p^{\ast }}{p_i}+\frac{\gamma -1}{2\gamma }}}& & & p^{\ast }>p_i& 激波\\ & & & & \\ \frac{2c_i}{\gamma -1}\left[{\left(\frac{p^{\ast }}{p_i}\right)}^{\frac{\gamma -1}{2\gamma }}-1\right]& & & p^{\ast }<p_i& 膨胀波\end{array}$$
得到关于压力$p^{\ast }$的方程
$$u_1-u_2=f(p^{\ast },p_1,{\rho }_1)+f(p^{\ast },p_2,{\rho }_2)\equiv F(p^{\ast })$$

采用数值方法求解即可得出$p^{\ast }$，然后可以算得$u^{\ast }$，跟情况1一样，再由式(11)来算出$Z_2$（下标1替换为2即可），最后用式(8)算出${\rho }^{\ast R}$（下标1替换为2即可），而${\rho }^{\ast L}$的计算可以通过式(18)求出：
$${\rho }^{\ast L}={\rho }_1{\left(\frac{p^{\ast }}{p_1}\right)}^{\frac{1}{\gamma }}$$

至此，5个未知数$Z_2$、$u^{\ast }$、$p^{\ast }$、${\rho }^{\ast L}$和${\rho }^{\ast R}$都求出来了，接下来求膨胀波内部的物理量。

先看膨胀波的边界范围，膨胀波向左传播，所以波头的传播速度为$Z_{1head}=u_1-c_1$，波尾的传播速度为$Z_{1tail}=u^{\ast }-c^{\ast L}$，那么在t时刻，波头位于$x=(u_1-c_1)t$，波尾位于$x=(u^{\ast }-c^{\ast L})t$位置。

膨胀波内部的物理量，利用特征相容关系计算，红线为从$x=0$处发出的左行特征线$dx/dt=u-c$，故其位置在t时刻为：
$$x/t=u-c$$

而该位置也可由另外一条特征线蓝线在0时刻的位置上右行而来，即特征线$dx/dt=u+c$，其上物理量满足$R_2$不变量，即：
$$u_1+\frac{2c_1}{\gamma -1}=u+\frac{2c}{\gamma -1}$$

联立这俩式子，可以求出$u$和$c$来，即
$$\{\begin{array}{ll}c(x,t)=\frac{\gamma -1}{\gamma +1}\left(u_1-\frac{x}{t}\right)+\frac{2c_1}{\gamma +1}& (21)\\ u(x,t)=c+x/t& (22)\end{array}$$

而膨胀波内部的压力和密度，则可由等熵关系来计算：
$$p=p_1(c/c_1{)}^{\frac{2\gamma }{\gamma -1}},\rho =\gamma p/c^2$$

至此，膨胀波内部的物理量是位置$x$和时间$t$的函数，且均可算出，情况2分析完毕。

2.3 右膨胀波的处理

其余情况与此类似，只是在处理右膨胀波时稍有差异，对于右膨胀波而言，1-3两区，满足Riemann不变量$R_2$（红色特征线上$dx/dt=u-c$）的相等，即
$$\{\begin{array}{ll}\frac{p^{\ast }}{({\rho }^{\ast R}{)}^{\gamma }}=\frac{p_2}{({\rho }_2{)}^{\gamma }}& \\ & \\ u_2-\frac{2c_2}{\gamma -1}=u^{\ast }-\frac{2c^R}{\gamma -1}& \end{array}$$

所以，推出来的速度和压力关系式为$u^{\ast }=u_2+f(p^{\ast },p_2,{\rho }_2)$，与之前是一样的，即左波是$-f$，右波是$+f$，形式仍旧是统一的。其求解$u^{\ast }$、$p^{\ast }$和${\rho }^{\ast R}$的方法和前面也是一样的。

只是在膨胀波的求解时，略有不同。

首先右膨胀波向右传播，所以波头的传播速度为$Z_{2head}=u_2+c_2$，波尾的传播速度为$Z_{2tail}=u^{\ast }+c^{\ast R}$，那么在t时刻，波头位于$x=(u_2+c_2)t$，波尾位于$x=(u^{\ast }+c^{\ast R})t$位置。

然后就是膨胀波内部物理量的计算，此时刚好与左膨胀波相反，利用特征相容关系计算时，右膨胀波为从$x=0$处发出的右行特征线$dx/dt=u+c$，故其位置在t时刻为：
$$x/t=u+c$$

而该位置也可由另外一条特征线在0时刻的位置上左行而来，即特征线$dx/dt=u-c$，其上物理量满足$R_2$不变量，阶：
$$u_2-\frac{2c_2}{\gamma -1}=u-\frac{2c}{\gamma -1}$$

联立这俩式子，可以求出$u$和$c$来，即，注意这里的式子和左膨胀波在正负号上略有区分
$$\{\begin{array}{l}c(x,t)=-\frac{\gamma -1}{\gamma +1}\left(u_2-\frac{x}{t}\right)+\frac{2c_2}{\gamma -1}\\ u(x,t)=-c+x/t\end{array}$$

而膨胀波内部的密度与压力的计算，还是用等熵关系，和左膨胀波时一样的，不再赘述。

3 Riemann问题的具体求解步骤

为便于程序实现，将Riemann问题的上述求解思路的具体步骤汇总如下

已知量为$u_1$、${\rho }_1$、$p_1$，$u_2$、${\rho }_2$、$p_2$，以及时刻$t$。

1. 判断可能出现的情况（五种情况之一）
   1.1. 定义函数
   $$f(p^{\ast },p_1,{\rho }_1)+f(p^{\ast },p_2,{\rho }_2)\equiv F(p^{\ast })$$
   其中，函数$f(p^{\ast },p_i,{\rho }_i)$为：
   $$f(p^{\ast },p_i,{\rho }_i)=\{\begin{array}{llccc}\frac{p^{\ast }-p_i}{{\rho }_i{c}_i\sqrt{\frac{\gamma +1}{2\gamma }\frac{p^{\ast }}{p_i}+\frac{\gamma -1}{2\gamma }}}& & & p^{\ast }>p_i& 激波\\ & & & & \\ \frac{2c_i}{\gamma -1}\left[{\left(\frac{p^{\ast }}{p_i}\right)}^{\frac{\gamma -1}{2\gamma }}-1\right]& & & p^{\ast }<p_i& 膨胀波\end{array}$$
   1.2. 判断属于哪种情况
   计算出$F(0)$、$F(p_1)$、$F(p_2)$，根据$u_1-u_2$的大小进行情况判断属于哪种类型。

2. 求解中心区域的压力和速度
   采用二分法或Newton法求解方程，获取压力$p^{\ast }$：
   $$u_1-u_2=F(p^{\ast })=f(p^{\ast },p_1,{\rho }_1)+f(p^{\ast },p_2,{\rho }_2)$$
   再由下式算出速度$u^{\ast }$
   $$u^{\ast }=\frac{1}{2}[u_1+u_2-f(p^{\ast },p_1,{\rho }_1)+f(p^{\ast },p_2,{\rho }_2)]$$

3. 求解中心区域接触间断两侧密度及左右波的传播速度
   3.1. 左波为激波的情况（情况1和3）
   左激波运动速度$Z_1$
   $$Z_1=u_1-\frac{p^{\ast }-p_1}{{\rho }_1(u_1-u^{\ast })}$$
   中心区域左侧密度${\rho }^{\ast L}$
   $${\rho }^{\ast L}=\frac{{\rho }_1(u_1-Z_1)}{(u^{\ast }-Z_1)}$$
   3.2. 左波为膨胀波的情况（情况2，4，5）
   波头速度$Z_{1head}$和波尾速度$Z_{1tail}$
   $$Z_{1head}=u_1-c_1,Z_{1tail}=u^{\ast }-c^{\ast L}$$
   注意对于情况5，其内部为真空，无法计算声速$c^{\ast L}$，其膨胀波的波尾速度为（这个不是很确定~）
   $$Z_{1tail\_case5}=u_1-\frac{2c_1}{\gamma -1}$$
   膨胀波内物理量的计算（$Z_{1head}t<x<Z_{1tail}t$）
   $$\{\begin{array}{l}c(x,t)=\frac{\gamma -1}{\gamma +1}\left(u_1-\frac{x}{t}\right)+\frac{2c_1}{\gamma -1}\\ u(x,t)=c+x/t\end{array}$$
   而膨胀波内部的压力和密度，则可由等熵关系来计算：
   $$p=p_1(c/c_1{)}^{\frac{2\gamma }{\gamma -1}},\rho =\gamma p/c^2$$
   3.3. 右波为激波的情况（情况1，2）
   右激波运动速度$Z_2$
   $$Z_2=u_2-\frac{p^{\ast }-p_2}{{\rho }_2(u_2-u^{\ast })}$$
   中心区域左侧密度${\rho }^{\ast R}$
   $${\rho }^{\ast R}=\frac{{\rho }_2(u_2-Z_2)}{(u^{\ast }-Z_2)}$$
   3.4. 右波为膨胀波的情况（情况3，4，5）
   波头速度$Z_{2head}$和波尾速度$Z_{2tail}$
   $$Z_{2head}=u_2+c_2,Z_{2tail}=u^{\ast }+c^{\ast R}$$
   注意对于情况5，其内部为真空，无法计算声速$c^{\ast R}$，其膨胀波的波尾速度为（这个不是很确定~）
   $$Z_{2tail\_case5}=u_2+\frac{2c_2}{\gamma -1}$$
   膨胀波内物理量的计算（$Z_{2tail}t<x<Z_{2head}t$）
   $$\{\begin{array}{l}c(x,t)=-\frac{\gamma -1}{\gamma +1}\left(u_2-\frac{x}{t}\right)+\frac{2c_2}{\gamma -1}\\ u(x,t)=-c+x/t\end{array}$$
   而膨胀波内部的压力和密度，则可由等熵关系来计算：
   $$p=p_2(c/c_2{)}^{\frac{2\gamma }{\gamma -1}},\rho =\gamma p/c^2$$

4. 生成数据，绘制图形，展示结果。

4 程序实现

程序采用matlab编写，较好实现和理解。
$f(p^{\ast },p_i,{\rho }_i)$函数

function [ f ] = P01_fPsPiRi( Ps, Pi, Ri )
%P01_FPSP1R1 f(Ps, Pi, Rhoi)函数
%   激波（膨胀波）一侧已知P和Rho，另一侧Ps，求取f的函数

gamma = 1.4;    % 理想气体比热比
Ci = sqrt(gamma * Pi / Ri); % 声速

if (Ps > Pi)
    f = (Ps - Pi) / (Ri * Ci) / ...
        sqrt((gamma + 1) / (2 * gamma) * (Ps / Pi) + ...
        (gamma - 1) / (2 * gamma));
end
if (Ps < Pi)
    f = 2 * Ci / (gamma - 1) * ...
        ((Ps / Pi) ^ ((gamma - 1) / (2 * gamma)) - 1);
end
if (Ps == Pi)
    f = 0;
end

end

判断情况的函数

function [ idxCase ] = P02_judgeCase( Fp0, Fp1, Fp2, U1, U2, P1, P2 )
%P02_JUDGECASE 判断属于哪种情况，依据F(0), F(p1), F(p2), 根据u2 - u1大小来判断
%   此处显示详细说明

U1_U2 = U1 - U2;
idxCase = 0;    % 情况标致
% p2>=p1, U1-U2对应区间 
% --5--Fp0--4--Fp1--3--Fp2--1-- ->
if P2 >= P1
    if (U1_U2) >= Fp2
        idxCase = 1;
    elseif (U1_U2) >= Fp1 && (U1_U2) < Fp2
        idxCase = 3;
    elseif (U1_U2) >= Fp0 && (U1_U2) < Fp1
        idxCase = 4;
	elseif (U1_U2) < Fp0
        idxCase = 5;
    end
end
% p2<=p1, U1-U2对应区间 
% --5--Fp0--4--Fp2--2--Fp1--1-- ->
if P2 <= P1
    if (U1_U2) >= Fp1
        idxCase = 1;
    elseif (U1_U2) >= Fp2 && (U1_U2) < Fp1
        idxCase = 2;
    elseif (U1_U2) >= Fp0 && (U1_U2) < Fp2
        idxCase = 4;
    elseif (U1_U2) < Fp0
        idxCase = 5;
    end
end

二分法求解中间区域压力$p^{\ast }$的函数，顺道把$u^{\ast }$一并计算好了

function [ Ps, Us ] = P03_solvePs( U1, P1, R1, U2, P2, R2 )
%P03_SOLVEPS 求解中心区的压力和速度
% 解方程 u1 - u2 = F(p*) = f(p*, p1, rho1) + f(p*, p2, rho2)
%   此处显示详细说明

PSpn = [0, 1e10];   % 压力一定是正值的，给个足够大的范围吧，0-10000MPa

U1_U2 = U1 - U2;

for iter = 1: 1000
    Ps = mean(PSpn);
    Fps = P01_fPsPiRi(Ps, P1, R1) + P01_fPsPiRi(Ps, P2, R2);
    if U1_U2 == Fps
        return;
    end
    if U1_U2 > Fps
        PSpn = [Ps, PSpn(2)];
    else
        PSpn = [PSpn(1), Ps];
    end
    if PSpn(2) - PSpn(1) < 1e-10
        Ps = mean(PSpn);
        break;
    end
end

Us = 0.5 * (U1 + U2 + P01_fPsPiRi(Ps, P2, R2) - P01_fPsPiRi(Ps, P1, R1));

end

左激波情况下计算激波运行速度$Z_1$和中间区域左侧密度${\rho }^{\ast L}$的函数

 function [ R1s, Z1 ] = P04_calcShockR1sZ1( P1, U1, R1, Ps, Us, gamma )
%P04_CALCRISZI 此处显示有关此函数的摘要
%   此处显示详细说明

Z1 = U1 - (Ps - P1) / (R1 * (U1 - Us));
R1s = R1 * (U1 - Z1) / (Us - Z1);

end

左膨胀波情况下计算波头波尾运行速度$Z_{1head}$和$Z_{1tail}$，以及中间区域左侧密度${\rho }^{\ast L}$的函数

 function [ R1s, Z1Head, Z1Tail ] = ...
 P05_calcExpanR1sZ1( P1, U1, R1, Ps, Us, gamma, idxCase )
%P05_CALCEXPANRISZI 此处显示有关此函数的摘要
%   此处显示详细说明

C1 = sqrt(gamma * P1 / R1);
Z1Head = U1 - C1;

if (idxCase ~= 5) 
    R1s = R1 * (Ps / P1) ^ (1 / gamma);
    C1s = sqrt(gamma * Ps / R1s);
    Z1Tail = Us - C1s;
end

% 对于情况5，中心区为真空，声速c1*无从计算，改由该式计算：
if (idxCase == 5)
    % 感觉好像不对……………………
    R1s = 0;    % 真空
    Z1Tail = U1 - 2 * C1 / (gamma - 1);   
end

end

右激波情况下计算激波运行速度$Z_2$和中间区域右侧密度${\rho }^{\ast R}$的函数，这个函数实际上和左激波的完全一样，没必要单独写一个出来的

function [ R2s, Z2 ] = P06_calcShockR2sZ2( P2, U2, R2, Ps, Us )
%P04_CALCSHOCKR2SZ2 此处显示有关此函数的摘要
%   此处显示详细说明

Z2 = U2 - (Ps - P2) / (R2 * (U2 - Us));
R2s = R2 * (U2 - Z2) / (Us - Z2);

end

右膨胀波情况下计算波头波尾运行速度$Z_{2head}$和$Z_{2tail}$，以及中间区域左侧密度${\rho }^{\ast R}$的函数

function [ R2s, Z2Head, Z2Tail ] = ...
    P07_calcExpanR2sZ2( P2, U2, R2, Ps, Us, gamma, idxCase )
%P07_CALCEXPANR2SZ2 此处显示有关此函数的摘要
%   此处显示详细说明

C2 = sqrt(gamma * P2 / R2);
Z2Head = U2 + C2;

if (idxCase ~= 5)
    R2s = R2 * (Ps / P2) ^ (1 / gamma);
    C2s = sqrt(gamma * Ps / R2s);
    Z2Tail = Us + C2s;
end

% 对于情况5，中心区为真空，声速c2*无从计算，改由该式计算：
if (idxCase == 5)
    % 感觉不太对……………………
    R2s = 0;    % 真空
    Z2Tail = U2 + 2 * C2 / (gamma - 1);
end

end

左膨胀波内部状态值$u,p,\rho$的计算函数，注意状态值是x和t的函数，所以直接用向量来存储了：

function [ xSpnLftExp, uSpnLftExp, pSpnLftExp, rSpnLftExp ] = ...
    P08_calcLftExpZone( Z1Head, Z1Tail, tNow, gamma, U1, C1, P1 )
%P08_CALCLFTEXPZONE 此处显示有关此函数的摘要
%   此处显示详细说明

xDwn = Z1Head * tNow;       xUp = Z1Tail * tNow;
xDlt = (xUp - xDwn) / 100;  xSpnLftExp = xDwn: xDlt: xUp;

cSpnLftExp = (gamma - 1) / (gamma + 1) * (U1 - xSpnLftExp / tNow) + ...
    2 / (gamma + 1) * C1;
uSpnLftExp = xSpnLftExp ./ tNow + cSpnLftExp;
pSpnLftExp = P1 .* (cSpnLftExp / C1) .^ (2 * gamma / (gamma - 1));
rSpnLftExp = gamma * pSpnLftExp ./ cSpnLftExp .^ 2;

end

右膨胀波内部状态值$u,p,\rho$的计算函数：

function [ xSpnRgtExp, uSpnRgtExp, pSpnRgtExp, rSpnRgtExp ] = ...
    P09_calcRgtExpZone( Z2Tail, Z2Head, tNow, gamma, U2, C2, P2 )
%P09_CALCRGTEXPZONE 此处显示有关此函数的摘要
%   此处显示详细说明

xDwn = Z2Tail * tNow;       xUp = Z2Head * tNow;
xDlt = (xUp - xDwn) / 100;  xSpnRgtExp = xDwn: xDlt: xUp;

cSpnRgtExp = - (gamma - 1) / (gamma + 1) * (U2 - xSpnRgtExp / tNow) + ...
    2 / (gamma + 1) * C2; % 注意有个负号
uSpnRgtExp = xSpnRgtExp ./ tNow - cSpnRgtExp; % 注意是减号
pSpnRgtExp = P2 .* (cSpnRgtExp / C2) .^ (2 * gamma / (gamma - 1));
rSpnRgtExp = gamma * pSpnRgtExp ./ cSpnRgtExp .^ 2;

end

计算左侧区域范围的函数

function [ xSpnLftWavL, pSpnLftWavL, uSpnLftWavL, rSpnLftWavL ] = ...
    P11_calcLftWaveLftZone( Z1, P1, U1, R1, tNow )
%P11_CALCLFTWAVELFTZONE 此处显示有关此函数的摘要
%   此处显示详细说明

lftShockX = Z1 * tNow;  % 左激波位置（或左膨胀波波头位置）
xSpnLftWavL = [min(-1, floor(lftShockX * 2)), lftShockX];
pSpnLftWavL = [P1, P1];
uSpnLftWavL = [U1, U1];
rSpnLftWavL = [R1, R1];  

end

计算中间区域位于间断左侧范围的函数

function [  xSpnMidL, pSpnMidL, uSpnMidL, rSpnMidL  ] = ...
    P12_calcMidLftZone( Z1, Ps, Us, RsL, tNow )
%P12_CALCMIDLFTZONE 此处显示有关此函数的摘要
%   此处显示详细说明

lftShockX = Z1 * tNow;  % 左激波位置（或左膨胀波波尾位置）
midDisconX = Us * tNow; % 接触间断面位置

xSpnMidL = [lftShockX, midDisconX];
pSpnMidL = [Ps, Ps];
uSpnMidL = [Us, Us];
rSpnMidL = [RsL, RsL];  

end

计算中间区域位于间断右侧范围的函数

function [ xSpnMidR, pSpnMidR, uSpnMidR, rSpnMidR ] = ...
    P13_calcMidRgtZone( Z2, Ps, Us, RsR, tNow )
%P13_CALCMIDRGTZONE 此处显示有关此函数的摘要
%   此处显示详细说明

rgtShockX = Z2 * tNow;  % 右激波位置（或右膨胀波波尾位置）
midDisconX = Us * tNow; % 接触间断面位置

xSpnMidR = [midDisconX, rgtShockX];
pSpnMidR = [Ps, Ps];
uSpnMidR = [Us, Us];
rSpnMidR = [RsR, RsR];

end

计算右侧区域范围的函数

function [ xSpnRgtWavR, pSpnRgtWavR, uSpnRgtWavR, rSpnRgtWavR ] = ...
    P14_calcRgtWavRgtZone( Z2, P2, U2, R2, tNow )
%P14_CALCRGTWAVRGTZONE 此处显示有关此函数的摘要
%   此处显示详细说明

rgtShockX = Z2 * tNow;  % 右激波位置（或右膨胀波波头位置）
xSpnRgtWavR = [rgtShockX, max(1, ceil(rgtShockX * 2))];
pSpnRgtWavR = [P2, P2];
uSpnRgtWavR = [U2, U2];
rSpnRgtWavR = [R2, R2]; 

end

几个区域合并成一个的代码段

% 把这几个区域合并起来啊
xSpn = [xSpnLftWavL, xSpnLftExp, xSpnMidL, xSpnMidR, xSpnRgtExp, xSpnRgtWavR];
uSpn = [uSpnLftWavL, uSpnLftExp, uSpnMidL, uSpnMidR, uSpnRgtExp, uSpnRgtWavR];
pSpn = [pSpnLftWavL, pSpnLftExp, pSpnMidL, pSpnMidR, pSpnRgtExp, pSpnRgtWavR];
rSpn = [rSpnLftWavL, rSpnLftExp, rSpnMidL, rSpnMidR, rSpnRgtExp, rSpnRgtWavR];

绘图展示的代码段

% 绘制图形
figure(99);
plot(xSpn, pSpn, xSpn, uSpn, xSpn, rSpn, 'LineWidth', 2);
legend('p', 'u', 'rho');
xlabel('x');    ylabel('p, u, rho');
title('Riemann Problem Accurate Solution');

最后是主程序，即按照第3部分的求解流程逐个调用子函数来完成求解

% 2020-02-19
% 梅冠华
% 求解Riemann问题的精确解
% Riemann问题，也称Reimann间断解，激波管问题，Sod激波管问题等
% 
% 控制方程：1D Euler方程
% 初始状态，左侧u1, rho1, p1; 右侧u2, rho2, p2; 
% 抽开两侧隔板，依据不同初始状态，会有5种情况出现
% 情况1：左激波 + 接触间断 + 右激波
% 情况2：左膨胀波 + 接触间断 + 右激波
% 情况3：左激波 + 接触间断 + 右膨胀波
% 情况4：左膨胀波 + 接触间断 + 右膨胀波
% 情况5：左膨胀波 + 右膨胀波

% 第5种情况没弄明白，其它的都还OK了！

clear,clc;

tNow = 0.14;    % 要计算的时刻t1

gamma = 1.4;    % 理想气体比热比

% 初始状态t0
U1 = 0;     R1 = 1;         P1 = 1;     % x < 0
U2 = 0;     R2 = 0.125;     P2 = 0.1;   % x > 0

C1 = sqrt(gamma * P1 / R1);
C2 = sqrt(gamma * P2 / R2);

% 定义函数F(p*) = f(p*, p1, rho1) + f(p*, p2, rho2)
% 计算F(0), F(p1), F(p2);
Fp0 = P01_fPsPiRi(0, P1, R1) + P01_fPsPiRi(0, P2, R2);
Fp1 = P01_fPsPiRi(P1, P1, R1) + P01_fPsPiRi(P1, P2, R2);
Fp2 = P01_fPsPiRi(P2, P1, R1) + P01_fPsPiRi(P2, P2, R2);

% stp 1
% 判断属于哪种情况，依据F(0), F(p1), F(p2), 根据u2 - u1大小来判断
idxCase = P02_judgeCase( Fp0, Fp1, Fp2, U1, U2, P1, P2 );

% stp 2
% 求解中心区的压力和速度
% 先求压力 u1 - u2 = F(p*) = f(p*, p1, rho1) + f(p*, p2, rho2)
% 再求速度 u* = 0.5*(u1+u2+f(p*, p2, rho2) - f(p*, p1, rho1))
[Ps, Us] = P03_solvePs(U1, P1, R1, U2, P2, R2);

% stp 3
% 确定中心区接触间断两侧的密度R1*, R2*, 以及左右波的传播速度Z1和Z2
% 中心接触间断左侧的物理量a, b
% a. 左波为激波的情况（情况1和3）
if (idxCase == 1) || (idxCase == 3)
    [RLs, Z1] = P04_calcShockR1sZ1( P1, U1, R1, Ps, Us );
end
% b. 左波为膨胀波（稀疏波）的情况（情况2, 4, 5）
if (idxCase == 2) || (idxCase == 4) || (idxCase == 5)
    [ RLs, Z1Head, Z1Tail ] = P05_calcExpanR1sZ1...
        ( P1, U1, R1, Ps, Us, gamma, idxCase );
end
% 中心接触间断右侧的物理量c, d
% c. 右波为激波的情况（情况1和2）
if (idxCase == 1) || (idxCase == 2)
    [R2s, Z2] = P06_calcShockR2sZ2( P2, U2, R2, Ps, Us );
end
% d. 右波为膨胀波（稀疏波）的情况（情况3, 4, 5）
if (idxCase == 3) || (idxCase == 4) || (idxCase == 5)
    [ R2s, Z2Head, Z2Tail ] = P07_calcExpanR2sZ2...
        ( P2, U2, R2, Ps, Us, gamma, idxCase );
end

% stp 4
% 计算稀疏波区域的值（如果有的话）
% a. 左稀疏波（情况2, 4, 5）
% Z1Head*t <= x <= Z1Tail*t
if (idxCase == 2) || (idxCase == 4) || (idxCase == 5)
    [ xSpnLftExp, uSpnLftExp, pSpnLftExp, rSpnLftExp ] = ...
        P08_calcLftExpZone( Z1Head, Z1Tail, tNow, gamma, U1, C1, P1 ); 
else % 整成这样方便后面合并处理
    xSpnLftExp = [];    uSpnLftExp = [];
    pSpnLftExp = [];    rSpnLftExp = [];
end
% b. 右稀疏波（情况3, 4, 5）
% Z2Tail*t <= x <= Z2Head*t
if (idxCase == 3) || (idxCase == 4) || (idxCase == 5)
    [ xSpnRgtExp, uSpnRgtExp, pSpnRgtExp, rSpnRgtExp ] = ...
        P09_calcRgtExpZone( Z2Tail, Z2Head, tNow, gamma, U2, C2, P2 ); 
else
    xSpnRgtExp = [];    uSpnRgtExp = [];
    pSpnRgtExp = [];    rSpnRgtExp = [];
end

% 计算各区域的存在范围，各区域的状态值，以便合成绘图
% ----左激波（或左膨胀波）左侧区域----左激波（或左膨胀波区域）---
% ----中间区域间断面左侧--接触间断--中间区域间断面右侧----
% ----右激波（或右膨胀波区域）----右激波（或右膨胀波）右侧区域----
% 左激波或左膨胀波左侧区域
% a. 左波为激波的情况（情况1和3）
if (idxCase == 1) || (idxCase == 3)
    [ xSpnLftWavL, pSpnLftWavL, uSpnLftWavL, rSpnLftWavL ] = ...
        P11_calcLftWaveLftZone(Z1, P1, U1, R1, tNow);
end
% b. 左波为膨胀波（稀疏波）的情况（情况2, 4, 5）
if (idxCase == 2) || (idxCase == 4) || (idxCase == 5)
    [ xSpnLftWavL, pSpnLftWavL, uSpnLftWavL, rSpnLftWavL ] = ...
        P11_calcLftWaveLftZone(Z1Head, P1, U1, R1, tNow);
end
% 左膨胀波区域（如果有的话）前面已经算好了
% 中间区域（接触间断左侧区域）
% a. 左波为激波的情况（情况1和3）
if (idxCase == 1) || (idxCase == 3)
    [ xSpnMidL, pSpnMidL, uSpnMidL, rSpnMidL ] = ...
        P12_calcMidLftZone(Z1, Ps, Us, RLs, tNow);
end
% b. 左波为膨胀波（稀疏波）的情况（情况2, 4, 5）
if (idxCase == 2) || (idxCase == 4) || (idxCase == 5)
    [ xSpnMidL, pSpnMidL, uSpnMidL, rSpnMidL ] = ...
        P12_calcMidLftZone(Z1Tail, Ps, Us, RLs, tNow);
end
% 中间区域（接触间断面右侧）
% a. 右波为激波的情况（情况1和2）
if (idxCase == 1) || (idxCase == 2)
    [ xSpnMidR, pSpnMidR, uSpnMidR, rSpnMidR ] = ...
        P13_calcMidRgtZone(Z2, Ps, Us, R2s, tNow);
end
% b. 右波为膨胀波（稀疏波）的情况（情况3, 4, 5）
if (idxCase == 3) || (idxCase == 4) || (idxCase == 5)
    [ xSpnMidR, pSpnMidR, uSpnMidR, rSpnMidR ] = ...
        P13_calcMidRgtZone(Z2Tail, Ps, Us, R2s, tNow);
end
% 右膨胀波区域（如果有的话）前面已经算好了
% 右激波或膨胀波右侧区域
% a. 右波为激波的情况（情况1和2）
if (idxCase == 1) || (idxCase == 2)
    [ xSpnRgtWavR, pSpnRgtWavR, uSpnRgtWavR, rSpnRgtWavR ] = ...
        P14_calcRgtWavRgtZone(Z2, P2, U2, R2, tNow);
end
% b. 右波为膨胀波（稀疏波）的情况（情况3, 4, 5）
if (idxCase == 3) || (idxCase == 4) || (idxCase == 5)
    [ xSpnRgtWavR, pSpnRgtWavR, uSpnRgtWavR, rSpnRgtWavR ] = ...
        P14_calcRgtWavRgtZone(Z2Head, P2, U2, R2, tNow);
end

% 把这几个区域合并起来啊
xSpn = [xSpnLftWavL, xSpnLftExp, xSpnMidL, xSpnMidR, xSpnRgtExp, xSpnRgtWavR];
uSpn = [uSpnLftWavL, uSpnLftExp, uSpnMidL, uSpnMidR, uSpnRgtExp, uSpnRgtWavR];
pSpn = [pSpnLftWavL, pSpnLftExp, pSpnMidL, pSpnMidR, pSpnRgtExp, pSpnRgtWavR];
rSpn = [rSpnLftWavL, rSpnLftExp, rSpnMidL, rSpnMidR, rSpnRgtExp, rSpnRgtWavR];


% 绘制图形
figure(99);
plot(xSpn, pSpn, xSpn, uSpn, xSpn, rSpn, 'LineWidth', 2);
legend('p', 'u', 'rho');
xlabel('x');    ylabel('p, u, rho');
title('Riemann Problem Accurate Solution');

% 结束
disp('done!');

5 运行结果

情况1

情况2

情况3，把情况2的初始条件左右对换一下，就是情况3了，结果也和情况2是一样的，只是左右对调，速度反向而已。

情况4

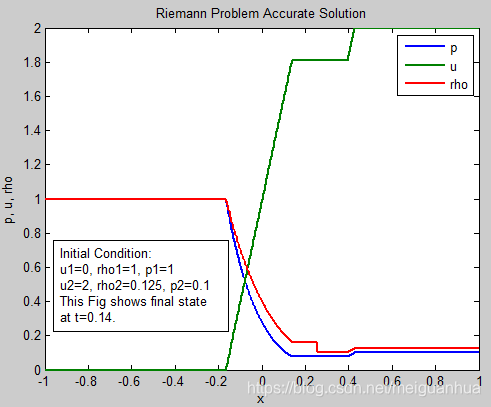
情况5，感觉不太对，波尾速度的计算好像不对，就不展示了。