Manache（马拉车）算法基本原理与python实现

 

马拉车算法：在元素向两边扩散进行查找的基本思路不变的情况下，充分利用回文串的对称性，大幅减少算法时间的一种算法（时间复杂度o(n)）。

 

字符的处理

在每个字符和字符串开头与结尾都添加上特殊符号“#”。然后在两端分别加入一个全新的符号，这样可以省去边界的判断。

如”aba“可以改写成”@#a#b#a#$“。

 

几个重要变量的初始化

建立列表p，并给其添加和字符串等数量的0，之后会用来记录每个元素向两边扩散所能达到的最大回文长度。

将max_right，max_mid_index初始化为0，前者用来记录已经观测到的所有回文串中右边界所能到达的最远的地方，后者则是这个回文串的对称点索引值。

 

主体循环

利用索引值进入循环（for i in range(1,len(s) - 1)）。

此时分三种情况：

第一种：

当i > max_right时，说明我们没法利用前面已知的数据来判断当前索引值下的元素扩散情况，因此我们让其向两边扩散查找最长回文串即可。查找完后这个回文串的右边界索引值必定大于max_right，故令max_right = i+p[i]-1。相应地，max_mid_index = i

第二种：

当i <= max_right时，根据回文串的对称性，可以令p[i]直接等于p[2*max_mid_index - i]，然后在此基础上继续向两边扩散看看能不能找到更长的回文串。

 

比如说，我们有”#a#b#a#”这个字符串，现在我们已经找到p[3] = 4（表示以b为中点的最长回文串可以由中心点向右延伸四位），因此此时max_right = 6,max_mid_index = 3。

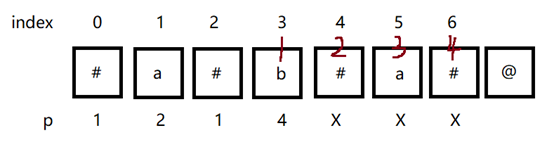
由回文串的对称性可知，回文串的前一部分和后一部分肯定是相反的，不然也不会称之为回文串。因此，p[4]可以直接等于p[2]。同理，p[5] = p[1] = 2，然后继续向两边扩散查看后面能否继续构成回文串。

 

第三种

i <= max_right，但是与p[i]对称的p[2*max_mid_index - i]超出了超出了右边界的范围，此时无论p[2*max_mid_index - i]的值多大，p[i]都要等与max_right – i + 1

 

例如以下字符串：

 

已经确定了p[5] = 4，右边界此时为8。于是轻松算的p[6]为1，但是若还是之前的逻辑，p[7]应该直接等于4了，这明显与理性的判断不符，原因在于此时“V”的索引值7+p[3] = 11已经超出边界了，超出的这一部分我们前面还没有接触过，并不知道是否为回文串，故只能先令p[7] = 右边界的索引值 – 索引值 + 1 = 2，然后继续判断s[9]是否等于s[5]，若等于，继续判断，并在判断结束后修改max_right,max_mid_index的值；若不等，则此时的p值确定。

经典题目：

leetcode 5.最长回文子串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2：

输入: "cbbd"
输出: "bb"

class Solution:
    def longestPalindrome(self, s: str) -> str:
        tem_s = '@#'
        for i in s:
            tem_s += i + '#'
        s = tem_s + '&'
        Lens = len(s)
        max_right = 0
        max_mid_index = 0
        p = [0] * Lens
        for i in range(1,Lens-1):
            if i > max_right:
                while s[i-p[i]] == s[i+p[i]]:
                    p[i] += 1
                max_right = i+p[i]-1
                max_mid_index = i
            else:
                p[i] = p[2*max_mid_index - i]
                if p[i] + i - 1 > max_right:
                    p[i] = max_right - i + 1
                while s[i-p[i]] == s[i+p[i]]:
                    p[i] += 1
                if i + p[i] - 1 > max_right:
                    max_right = i+p[i]-1
                    max_mid_index = i
        index = p.index(max(p))
        return s[index - p[index] + 1:index + p[index]].replace('#','')

leetcode 647.回文子串

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入："abc"
输出：3
解释：三个回文子串: "a", "b", "c"

示例 2：

输入："aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

 

提示：

输入的字符串长度不会超过 1000 。

class Solution:
    def countSubstrings(self, s: str) -> int:
        tem_s = '@#'
        for i in s:
            tem_s += i + '#'
        s = tem_s + '&'
        Lens = len(s)
        max_right = 0
        max_mid_index = 0
        p = [0] * Lens
        for i in range(1,Lens-1):
            if i > max_right:
                while s[i-p[i]] == s[i+p[i]]:
                    p[i] += 1
                max_right = i+p[i]-1
                max_mid_index = i
            else:
                p[i] = p[2*max_mid_index - i]
                if p[i] + i - 1 > max_right:
                    p[i] = max_right - i + 1
                while s[i-p[i]] == s[i+p[i]]:
                    p[i] += 1
                if i + p[i] - 1 > max_right:
                    max_right = i+p[i]-1
                    max_mid_index = i
        ans = 0
        for i in p:
            ans += int(i/2)
        return ans