1 图(graph)、顶点(vertices)、边(edges)
图由顶点和边组成,是表示物件与物件(objects)之间的关系的方法。在其他的术语中,图也被称作网络(network),顶点被称作结点(nodes),边被称作链接(links)。
图的数学表示:![]() ,其中V是顶点集:
,其中V是顶点集: ; E是边集:
; E是边集:
2 顶点相邻(adjacent)
两个顶点被一条边相连,就说这两个顶点是相邻的(换句话讲,如果说某两个顶点是相邻的,也就是指这两个顶点之间有边),这两个顶点互为邻居顶点(neighbor vertices)。如图1(a)中,顶点A与顶点B、C、D相邻,与顶点E不相邻,B、C、D都是A的邻居顶点。

图1:(a)无向图(undirected graph),有向图(directed graph),无向权重图(weighted undirected graph)
3 聚类系数(clustering coefficient)
顶点的聚类系数:一个顶点,它有K个邻居顶点【邻居顶点概念见上边“2 顶点相邻“】,这k个邻居顶点之间实际存在的边的个数比上这k个邻居顶点最多可能存在的边的个数(也即 ),这个比值就是这个顶点的聚类系数。
),这个比值就是这个顶点的聚类系数。
如图2(a)中蓝色顶点有3个白色邻居顶点,这3个邻居顶点实际有边3条(黑色加粗线条所示),而3个邻居顶点最多可能边数是3*(3-1)/2=3 ,因此最后的聚类系数CC=3/3=1
如图2(b)中蓝色顶点有3个白色邻居顶点,这3个邻居顶点实际有边1条(黑色加粗线条所示),而3个邻居顶点最多可能边数是3*(3-1)/2=3 ,因此最后的聚类系数CC=1/3
如图2(c)中蓝色顶点有3个白色邻居顶点,这3个邻居顶点实际有边0条(黑色加粗线条所示),而3个邻居顶点最多可能边数是3*(3-1)/2=3 ,因此最后的聚类系数CC=0
顶点的聚类系数又被称为局部聚类系数(local clustering coefficient)。



图2:顶点的聚类系数(a)CC=1 (b)CC=1/3 (c)CC=0
图的聚类系数:一个图中所有顶点的聚类系数的平均值为这个图的聚类系数。也被称作网络的平均聚类系数(networkaverage clustering coefficient)
4 顶点的度(degree),图的平均度(average degree),度分布(degree distribution)
顶点的度:一个顶点的度是指与该顶点相连的边的个数。有向图的顶点的度还可以细分为入度和出度,入度是以该顶点为头(head)的边的条数,出度是以该顶点为尾(tail)的边的条数。
如图1(a)中 顶点A的度是3,图1(b)中顶点A的度是3,其中入度是1,出度是2。
一个图的平均度(average degree)是:
![]()
其中N是图中顶点的个数。
一个图的度分布是:整个图中顶点的度的概率分布。
例如,如果一个图共有N个顶点,其中Ni个顶点的度是K,那么这个图的度分布P(K)=Ni/N。
很多社会网络的度分布服从幂法则(power law),即 。
。
幂律分布也称为无标度分布(scale free distribution)。
5 完全图(complete graph)
每一对不同顶点恰有一条边相连,即每一对不同顶点都是相邻的,则一个图称为完全图。
n个端点的完全图以Kn 表示,有n个端点及 条边【完全图的n个顶点的任意两个顶点恰有一条边,求边数相当于一个组合问题】。举例如下图:
条边【完全图的n个顶点的任意两个顶点恰有一条边,求边数相当于一个组合问题】。举例如下图:

图3:完全图举例
6 派系(clique)
一个无向图的一个派系是指:这个无向图的顶点集有这样一个子顶点集,子顶点集里的任意两个顶点都有一条边相连(也即子顶点集中的任意两个顶点都是相邻的),那么这个子顶点集及其边构成的图就是这个无向图的一个派系。如果这个派系的顶点有k个,就称这个派系为k-派系(k-clique)。
其实也就是一个无向图里的一个子完全图就是这个无向图的一个派系。
下面这个图共有23个1-派系(也即这个图的所有顶点个数)、42个2-派系(也即图中的所有边)、19个3-派系(图中所有蓝色区域标出的三角形)、2个4-派系(图中深蓝区域的四边形)

图4:派系举例
7 路径(path),简单路径(simple path), 最短路径(shortest path),平均最短路径长度(average shortest path length),图的直径(diameter),连通图(connected graph),连通分量(connected component)
路径:如图1(a)中,[A-B-E-C]就是顶点A到顶点C的一条路径。
简单路径:路径中没有重复顶点的路径叫做简单路径,[A-B-E-C]就是一条简单路径。
最短路径:如图1(a)中,顶点A到顶点C的最短路径是 [A-C]
平均最短路径长度:一个图中所有任意两点间的最短路径的平均值。
图的直径:图中所有的任意两顶点间的最短路径中,最长的那个最短路径被定义为这个图的直径。
连通图:图中任意两顶点都可以由一条路径连接起来,这个图就是连通图。
连通分量:一个图的最大的连通的子图。
8 图的类型:二分图(Bipartite graphs),随机图(Random graphs),正则图(Regular graphs),无标度图(Scale-free graphs),小世界图(Small-world graphs)
二分图:一个无向图的顶点集可分割为两个互不相交的子集,并且图中每条边所关联的两个顶点分别属于这两个不同的顶点子集(也就是说每个顶点子集里的顶点不相邻),这个图可以称为一个二分图。
下图就是一个二分图,因为这个图的顶点集可以这样划分:{1,2,3}和{4,5,6,7},顶点子集{1,2,3}中的三个顶点不相邻,顶点子集{4,5,6,7}中的四个顶点也不相邻,符合二分图条件。

图5:二分图
随机图:图中的边是随机生成的,即任意两个顶点之间有一条边的概率为P。
正则图:如果图中所有顶点的度皆相等,则此图称为正则图。
无标度图:图的度分布服从幂律分布的图为无标度图。
小世界图:图中任意两个顶点之间的路径都非常小的图(例如地球上任意两个人之间的平均距离是6,人际关系图就是一个小世界图)。
9 两个图的积:笛卡尔积图(Cartesian product graph),直积图(direct product graph),图的合成图(Lexicographical product graph)
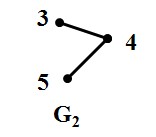
两个图的积是指由两个图G1 和 G2 生成一个新图 H 的操作:要求 新图H 的顶点集(vertex set)是 G1 和G2顶点集的笛卡尔积,即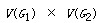
图5:G1和G2
如图5所示两图,G1 和G2的各类积图定义如下:
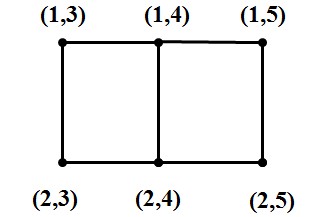
笛卡尔积图:对于顶点集V=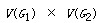
(注:adj 是 adjacent 相邻的缩写, 在G1中 u1 adj v1,即指 u1 和 v1在图G1中相邻,也即u1和v1之间在图G1中有边相连。)
例子:根据定义,G1和G2的笛卡尔积图的顶点集是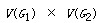
图6:G1和G2的笛卡尔积图
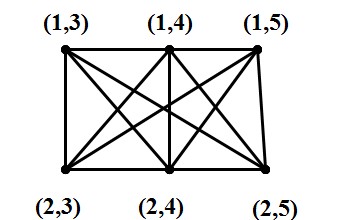
直积图:对于顶点集V=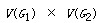
例子:根据定义,G1和G2的直积图的顶点集是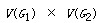
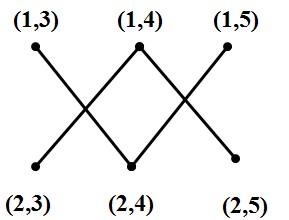
图7:G1和G2的直积图
合成图:对于顶点集V=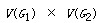
例子:根据定义,G1和G2的合成图的顶点集是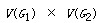
图8:G1和G2的合成图G1[G2]
参考
《复杂网络理论及其应用》
《GRAPH-BASED NATURAL LANGUAGE PROCESSING AND INFORMATION RETRIEVAL》
Wikipedia:clustering coefficient,Path(social network),complete graph,clique(graph theory),degree distribution ,graph product
转载请注明出处 http://blog.csdn.net/minenki/article/details/8606515








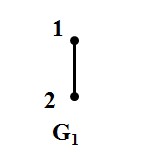














 781
781











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








