算法设计与分析 (2. 递归与分治策略)

2.1 递归的概念

• 直接或间接地调用自身的算法称为递归算法

例2.1 累加函数

• 累加函数可递归地定义为：
  $$s(n)=\{\begin{array}{ll}1,& n=1;\\ s(n-1)+n,& n>1.\end{array}$$

public static int sum(int n){
    if (n == 1) return 1;
    return sum(n - 1) + n;
}

• 每个递归函数都必须有非递归定义的初始值

讨论

• 该算法的时间、空间复杂度
• 如何改进该算法，并分析复杂度

例2.2 Fibonacci数列

$$F(n)=\{\begin{array}{ll}1,& n=0,1;\\ F(n-1)+F(n-2),& n>1.\end{array}$$

public static int fibonacci(int n){
    if (n <= 1) return 1;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

• 由递归式可知，需要两个初始值 (有时更多)

例2.3 Ackerman函数

$$\{\begin{array}{ll}A(1,0)=2;& \\ A(0,m)=1,& m\ge 0;\\ A(n,0)=n+2,& n\ge 2;\\ A(n,m)=A(A(n-1,m),m-1),& n,m\ge 1.\end{array}$$

• 仅有部分递归函数可以简化为非递归函数 (其内容为组合数学所研究)

例2.6 Hanoi塔问题

public static void hanoi(int n, int a, int b, int c){
	if (n > 0){
    	hanoi(n - 1, a, c, b);
    	System.out.println(a + “->” + b);
	    hanoi(n - 1, c, b, a);
	 }//Of if
}//Of hanoi

注意：

• 没写else，因为n = 0时不需要移动
• 如果跟踪该算法，建议不超过两层调用
  

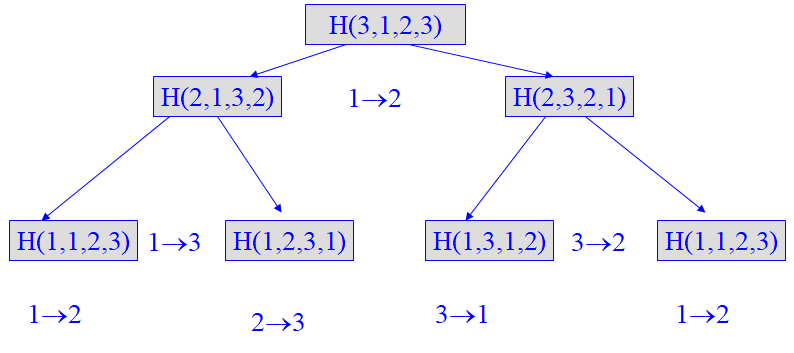
讨论

• Hanoi问题递归算法的空间复杂度、时间复杂度分别为多少?
• Hanoi问题能被有效地自动化吗?
• 如果把问题改成: 如果有 $n$ 个盘子, 求第 $k$ 步移动的源塔与目标塔呢?

2.2 分治法的基本思想

• 将一个规模为n的问题分解为k个规模较小的问题, 这些子问题相互独立且与原问题相同. 递归地解这些子问题, 然后将各子问题的解合并得到原问题的解.
• 平衡子问题: 尽量使各子问题规模相同

递归方程

$$T(n)=\{\begin{array}{ll}O(1),& n=1;\\ kT(n/m)+f(n),& n>1.\end{array}\text{\hspace{1em}(1)}$$

• 推导
  $$\begin{array}{ll}T(n)& =kT(n/m)+f(n)\\ & =k(kT(n/m^2)+f(n/m))+f(n)\\ & =k(k(kT(n/m^3)+f(n/m^2))+f(n/m))+f(n)\\ & =k^{3}T(n/m^3)+k^{2}f(n/m^2))+kf(n/m))+f(n)\\ & =\dots \\ & =k^{\log m^n}+{\sum }_{j=0}^{\log m^n-1}{k}^{j}f(n/m^j)\\ & =n^{\log m^k}+{\sum }_{j=0}^{\log m^n-1}{k}^{j}f(n/m^j)\end{array}\text{\hspace{1em}(2)}$$

2.3 二分搜索技术

• 条件：已排序
• 方法：每次将元素分成大致相同两半, 取中间数据进行比较，找到该数据或者将搜索范围减半
• 讨论: 利用 (1)(2) 式进行时间复杂度分析
• 讨论: 有若干质量介于 1 克至1000克（仅可能为整数）的物体, 为称出它们的质量, 需要多少个砝码?

课堂练习: 习题 2-3

设 $a[0:n-1]$ 是已排好序的数组. 请改写二分搜索算法, 使得当搜索元素 $x$ 不要数组中时, 返回小于 $x$ 的最大元素位置 $i$ 和大于 $x$ 的最小元素位置 $j$. 当搜索元素在数组中时, $i$ 和 $j$ 相同, 均为 $x$ 在数组中的位置.

附加练习

分别写出二分搜索的递归与非递归实现.
可参考 日撸 Java 300 行 第 41 天.

2.4 大整数的乘法

• 小学乘法
  
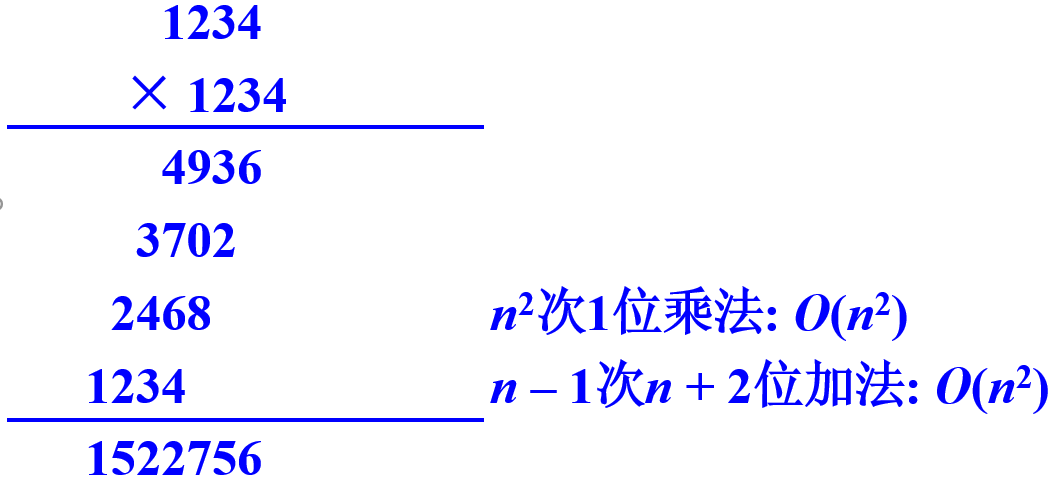
• 改进算法
  对二进制数 $X$ 与 $Y$, 令前一半高位和后一半低位分别为 $A$, $C$ 与 $B$, $D$.
  $$\begin{array}{ll}XY& =AC{2}^n+(AD+BC)2^{n/2}+BD\\ & =AC{2}^n+((A-B)(D-C)+AC+BD)2^{n/2}+BD\end{array}$$
• 对应到 (1) 式,
  $m=2$
  $k=3$
  $f(n)=O(n)$
• 问题: 代入 (2) 式, 时间复杂度为多少?

课堂练习: 习题 2-5

将 $X$ 和 $Y$ 都分成长度为 $n/3$ 的 3 段, 应如何设计? 其复杂度为多少?

• 讨论: 利用 (1)(2) 式进行归并排序的时间复杂度分析
  提示: 并归排序每轮需要比较和拷贝各 $n$ 次, 每次将问题变成两个子问题, 规模降一半.

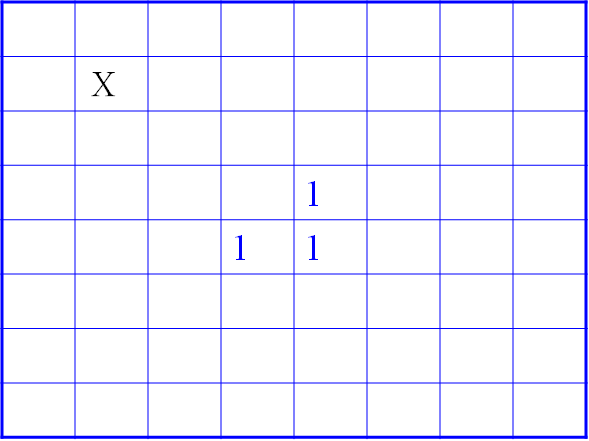
2.6 棋盘覆盖

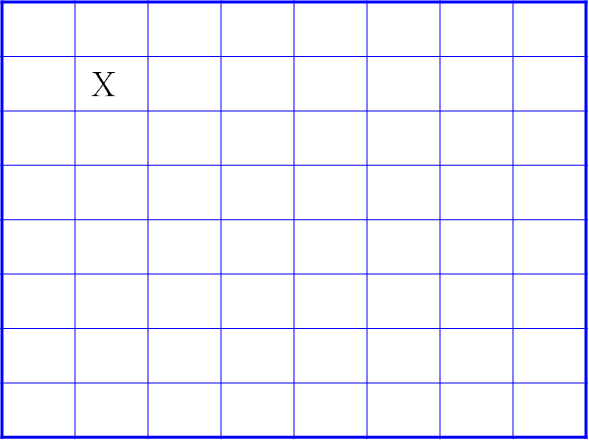
• 问题: $2^k\times 2^k$ 的棋盘中, 有一个位置已经被占据, 使用 L 型牌将其它位置覆盖, 应该如何做?
• 方案: 通过在其它三个部分分别占住一, 将其分解为 4 个 $2^{k-1}\times 2^{k-1}$ 的子问题.
  

2.7 归并排序

• 基本思想
  将待排元素分成大小大致相同的两个子集, 分别对它们进行排序, 最终将排好序的子集合并成为所要求的集合.

public void mergeSort(int a[], int left, int right){
    if (left < right){
        int i = (left + right)/2;
        mergeSort(a, left,  i);
        mergeSort(a, i + 1,  right);
        merge(a, b, left, i, right);
        copy(b, a, left, right); // Copy back
    }
}

• 两个已排序数组的合并
  

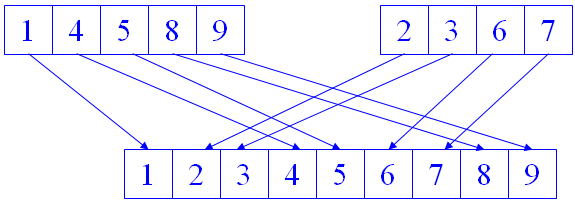
• 算法跟踪
  $a=[7,2,5,6,9,4]$, 分析其合并排序过程。S表示mergeSort，m表示merge
  

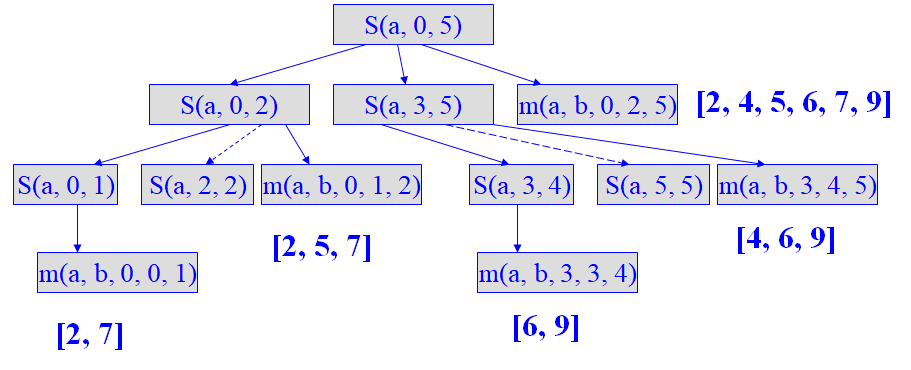
• 用 (1)(2) 式进行复杂度分析

• 讨论: 将其改造为非递归形式有什么好处?

附加练习

写出合并排序的非递归实现.
可参考 日撸 Java 300 行 第 49 天.

2.11 循环赛日程表

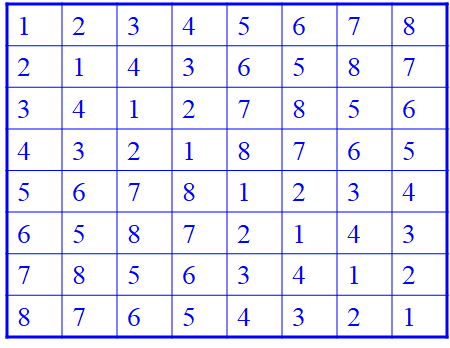
习题2-34

Gray 码是一个长度为 $2n$ 的序列. 序列中无相同元素, 每个元素都是长度为 $n$ 的串, 相邻元素恰好只有 1 位不同. 用分治策略设计一个算法对任意的 $n$ 构造相应的 Gray 码.

$n=1$: 0, 1
$n=2$: 00, 10, 11, 01
$n=3$: 000, 100, 110, 010, 011, 111, 101, 001

小结

• 递归算法的优点
  结构清晰, 可读性强, 容易用数学归纳法证明其正确性. 通常也容易分析其时间、空间复杂度.