1. 问题
f
(
x
)
=
1
1
+
e
−
x
(1)
f(x) = \frac{1}{1 + e^{-x}} \tag{1}
f(x)=1+e−x1(1)
x
∼
N
(
μ
,
σ
2
)
(2)
x \sim \mathcal{N}(\mu, \sigma^2) \tag{2}
x∼N(μ,σ2)(2)
(1)
f
(
x
)
f(x)
f(x) 的分布密度能否导出?
(2)
f
(
x
)
f(x)
f(x) 的均值方差如何计算？
2. 解:
列出正态分布式子:
p
(
x
)
=
1
2
π
σ
e
−
(
x
−
μ
)
2
2
σ
2
(3)
p(x) = \frac{1}{\sqrt{2 \pi}\sigma}e^{-\frac{(x - \mu)^2}{2 \sigma^2}} \tag{3}
p(x)=2πσ1e−2σ2(x−μ)2(3)
由式 (1) 可知,
y
=
f
(
x
)
y = f(x)
y=f(x) 的取值范围为
(
0
,
1
)
(0, 1)
(0,1). 应满足
∫
0
1
p
(
y
)
=
1.
(4)
\int_{0}^{1} p(y) = 1. \tag{4}
∫01p(y)=1.(4)
2.1 密度函数的计算
需要导出
p
(
y
)
p(y)
p(y).
P
(
y
≤
α
)
=
∫
0
α
p
(
y
)
d
y
=
P
(
x
≤
f
−
1
(
α
)
)
=
∫
−
∞
f
−
1
(
α
)
p
(
x
)
d
x
(5)
P(y \leq \alpha) = \int_{0}^\alpha p(y) d y= P(x \leq f^{-1}(\alpha)) = \int_{-\infty}^{f^{-1}(\alpha)} p(x)d x \tag{5}
P(y≤α)=∫0αp(y)dy=P(x≤f−1(α))=∫−∞f−1(α)p(x)dx(5)
这里是我的版本:
使用反函数, 获得下式 (这是一个充分条件，但我不知道是否必要):
p
y
(
x
)
=
p
x
(
f
−
1
(
x
)
)
(6)
p_y(x) = p_x(f^{-1}(x)) \tag{6}
py(x)=px(f−1(x))(6)
继续代入可得
p
y
(
x
)
=
p
x
(
ln
x
1
−
x
)
=
1
2
π
σ
e
−
(
ln
x
1
−
x
−
μ
)
2
2
σ
2
(7)
p_y(x) = p_x\left(\ln \frac{x}{1-x}\right) = \frac{1}{\sqrt{2 \pi}\sigma}e^{-\frac{\left(\ln \frac{x}{1-x} - \mu\right)^2}{2 \sigma^2}} \tag{7}
py(x)=px(ln1−xx)=2πσ1e−2σ2(ln1−xx−μ)2(7)
注意
x
∈
(
0
,
1
)
x \in (0, 1)
x∈(0,1).
以下是罗皓的推导.
先求反函数:
f
−
1
(
y
)
=
ln
y
1
−
y
(8)
f^{-1}(y) = \ln \frac{y}{1 - y} \tag{8}
f−1(y)=ln1−yy(8)
对反函数求导:
(
f
−
1
(
y
)
)
′
=
1
1
−
y
(9)
(f^{-1}(y))' = \frac{1}{1 - y} \tag{9}
(f−1(y))′=1−y1(9)
分布函数
G
(
y
)
=
P
{
η
≤
y
}
=
P
{
f
(
ξ
≤
y
)
}
=
∫
f
(
x
)
≤
y
p
(
x
)
d
x
(10)
G(y) = P\{\eta \leq y\} = P\{f(\xi \leq y)\} = \int_{f(x) \leq y} p(x) dx \tag{10}
G(y)=P{η≤y}=P{f(ξ≤y)}=∫f(x)≤yp(x)dx(10)
因为这里的
f
(
x
)
f(x)
f(x) 是单增函数, 上述积分可以直接代算的, 亦
ξ
\xi
ξ 理解为把
{
ξ
∣
f
(
ξ
)
<
y
}
\{\xi | f(\xi) < y\}
{ξ∣f(ξ)<y} 关于
ξ
\xi
ξ 的等价事件, 即
f
(
x
)
≤
y
⇔
f
−
1
(
f
(
x
)
)
≤
f
−
1
(
y
)
(11)
f(x) \leq y \Leftrightarrow f^{-1}(f(x)) \leq f^{-1}(y) \tag{11}
f(x)≤y⇔f−1(f(x))≤f−1(y)(11)
即
x
≤
f
−
1
(
y
)
x \leq f^{-1}(y)
x≤f−1(y).
则
G
(
y
)
=
P
{
f
(
ξ
)
≤
y
}
=
P
{
ξ
≤
f
−
1
(
y
)
}
=
F
(
f
−
1
(
y
)
)
(12)
G(y) = P\{f(\xi) \leq y\} = P\{\xi \leq f^{-1}(y)\} = F(f^{-1}(y)) \tag{12}
G(y)=P{f(ξ)≤y}=P{ξ≤f−1(y)}=F(f−1(y))(12)
此时
p
(
y
)
=
G
′
(
y
)
=
d
(
F
(
f
−
1
(
y
)
)
)
d
(
f
−
1
(
y
)
)
⋅
d
(
f
−
1
(
y
)
)
d
y
=
p
(
f
−
1
(
y
)
)
(
f
−
1
(
y
)
)
′
(13)
p(y) = G'(y) = \frac{d(F(f^{-1}(y)))}{d(f^{-1}(y))} \cdot \frac{d(f^{-1}(y))}{dy} = p(f^{-1}(y))(f^{-1}(y))'\tag{13}
p(y)=G′(y)=d(f−1(y))d(F(f−1(y)))⋅dyd(f−1(y))=p(f−1(y))(f−1(y))′(13)
最后
p
(
y
)
=
1
y
(
1
−
y
)
⋅
1
2
π
σ
e
−
(
ln
y
1
−
y
−
μ
)
2
2
σ
2
(14)
p(y) = \frac{1}{y(1-y)} \cdot \frac{1}{\sqrt{2 \pi}\sigma}e^{-\frac{\left(\ln \frac{y}{1-y} - \mu\right)^2}{2 \sigma^2}} \tag{14}
p(y)=y(1−y)1⋅2πσ1e−2σ2(ln1−yy−μ)2(14)
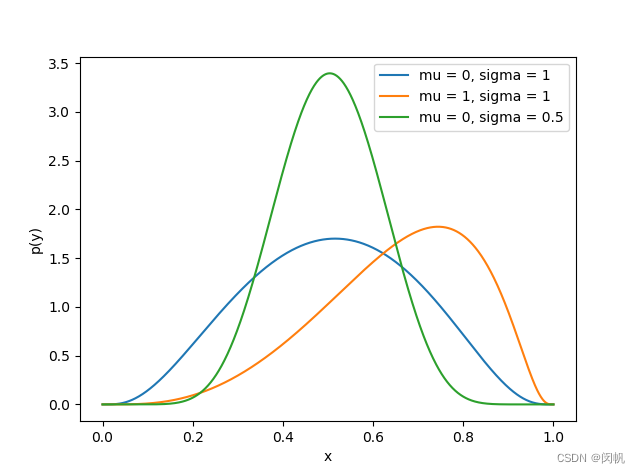
2.2 均值的计算
由 sigmoid 函数与正态分布函数的对称性可知 (我都不知道自己是怎么胡扯出来的):
E
(
x
)
=
f
(
μ
)
=
1
1
+
e
−
μ
(8)
E(x) = f(\mu) = \frac{1}{1 + e^{-\mu}} \tag{8}
E(x)=f(μ)=1+e−μ1(8)
特别地, 当
μ
=
0
\mu = 0
μ=0 时,
E
(
x
)
=
0.5
E(x) = 0.5
E(x)=0.5.
2.3 方差的计算
这个真不会了. 罗皓也没获得化简的式子. 还是把他难看的真迹秀一下.
2056
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
