GESP 2025年3月C++ 5级 真题与解析

答案：A

解析：链表需要循序访问，不能随机访问任何一个元素。

答案：A

解析：一眼就不对，p->next->prev原来指向p，现在指向p->next，就是自己。P->prev->next原来指向p，现在指向p->prev，也是自己。所以链断了。

答案：B

解析：A，head的前驱不需要赋值；C，tail的后驱不需要赋值；D，tail没有连上head

答案：B

解析：代入即可

答案：D

解析：唯一分解定理，每一项都是质因数

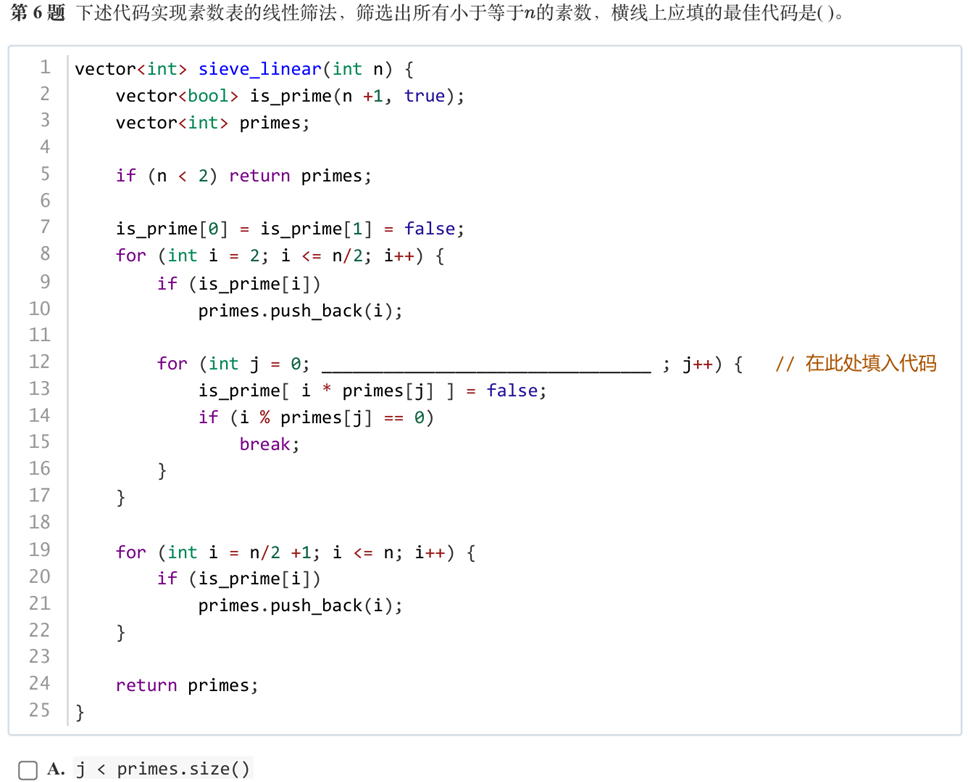
答案：C

解析：把当前所有小于n的i的倍数都设为不是质数

答案：A

解析：递归时函数的参数和结果保存在“栈”中。

答案：D

解析：factorialB不是递归

答案：A

解析：选择排序在交换时，可能会把后面的相等元素移动到前面，破坏原始顺序。

答案：B

解析：1.由于i=low-1,所以要先i++;2.由于基准是每段的末尾，所以先要把小于基准的数堆到当前分段的前部。

答案：C

解析：⌈log2​100⌉=7，向上取整

答案：A

解析：避免整数溢出：(left + right) 在 left 和 right 很大时可能溢出，但 left + (right - left) / 2 不会。等价于 (left + right) / 2，但更安全。

答案：A

解析：贪心的核心是先选择，选择当前最优解，但贪心不是一定能找到最优解。

答案：D

解析：首先排除A，然后排除C，return 0不可能获得最大值，且还return leftMax*rightMax，就更不符合逻辑。最后排除B，return leftMax+rightMax不符合逻辑。

答案：B

解析：carry是上一位的进位值，所以选B

答案：T

解析：注意，这里是将p的“值”设为p->next的值，不是将p=p->next。是p.val=p->next->val。

答案：F

解析：链表中的存储单元是动态分配的，不需要连续。

答案：T

解析：如题所述。

答案：F

解析：贪心做的的最有选择，不一定是最优解。      

答案：T

解析：如题所述。

答案：F

解析：快排平均复杂度为为O(nlogn)，最差为O（n2）

答案：T

解析：如题所述。

答案：F

解析：只适用于有序数组

答案：F

解析：贪心

答案：T

解析：如题所述。

解题思路

这是一个分配问题，可以转化为选择哪些物品分配给 B，哪些分配给 C，使得总收入最大。
由于 B 和 C 各自必须买 n 件，我们需要找到一种最优分配策略。

关键观察

• 如果第 i 件物品分配给 B，收入增加 b_i。
• 如果分配给 C，收入增加 c_i。
• 决策因素：选择 b_i - c_i 较大的物品优先给 B（因为这样“损失”更小）。

什么是“损失”？

• 如果把第 i件物品分配给 B，则收入是 bi。
• 如果分配给 C，则收入是 ci。
• “损失”：如果本可以分配给 B（因为 bi>ci​），但错误地分配给了 C，那么你会“损失” bi−ci的潜在收入。

因此：

• bi−ci越大，说明分配给 B 比分配给 C 更有利（即“损失”更大如果没选 B）。
• bi−ci越小（甚至是负数），说明分配给 C 更有利。

注意：必须取差值最大，取值最大是不对的。比如：

6 7  9 11

1 10 11 12

这里取的是(6,11)和（10,11），和为38，即差值最大，而不是(6,7)和(11,12)，和为36。

代码

#include <bits/stdc++.h>

 using namespace std;

 const int N = 2e5 + 5;

 int n;

 long long b[N], c[N], d[N];

 long long ans;

 int main() {

    scanf("%d", &n);

    for (int i = 1; i <= 2 * n; i++)

        scanf("%lld", &b[i]);

    for (int i = 1; i <= 2 * n; i++)

        scanf("%lld", &c[i]);

    for (int i = 1; i <= 2 * n; i++) {

        ans += b[i];

        d[i] = c[i] - b[i];                 //求两个价格的差值

    }

    sort(d + 1, d + 2 * n + 1);                                    

    for (int i = n + 1; i <= 2 * n; i++)    //加上c-b的n个差值，注意这里是从n+1开始

        ans += d[i];

    printf("%lld\n", ans);

    return 0;

 }

思路：重点：根据群论基本定理和数论中的阶的性质：

1. 欧拉定理保证：对任何与p互质的a，都有a^φ(p) ≡ 1 mod p

2. 最小性约束：若存在更小的k满足a^k ≡ 1 mod p，则这个k必须是φ(p)的约数

3. 约数必然性证明：

  假设存在k是最小正整数使a^k ≡ 1，但k不整除φ(p)

  用辗转相除法：设d = gcd(k, φ(p))，则存在整数x,y使d = kx + φ(p)y

  可得a^d ≡ 1 mod p（因1^x * 1^y = 1）

  这与k的最小性矛盾（因d < k）

参考程序

//2025年3月五级考试

//原根判断

#include <cstdio>

 using namespace std;

 int a, p;

 int ans;

 int fpw(int b, int e) {            //快速幂

    if (e == 0)

        return 1;

    int r = fpw(b, e >> 1);

    r = 1ll * r * r % p;

    if (e & 1)

        r = 1ll * r * b % p;

    return r;

 }

 void check(int e) {

    if (fpw(a, e) == 1)

        ans = 0;

 }

 int main() {

    int T;

    scanf("%d", &T);

    while (T--) {

        scanf("%d%d", &a, &p);

        ans = 1;

        int phi = p - 1, r = phi;

        for (int i = 2; i * i <= phi; i++)//最小性约束：若存在更小的k满足a^k ≡ 1 mod p，则这个k必须是φ(p)的约数

            if (phi % i == 0) {    

                check(phi / i);

                if(ans == 0)

                    break;

                while (r % i == 0)

                    r /= i;

            }

        if (ans && r > 1)  

            check(phi / r);

        printf(ans ? "Yes\n" : "No\n");

    }

    return 0;

 }

学编程、玩信奥，微信搜“信奥莫老师”，或关注微信公众号“AI之上-信奥驿站”