算法竞赛进阶指南 0x30 数学知识
本书有在线测评网站的支持,是一大亮点,又是NOI经历者编写的,故赶紧入手一本,抓紧时间研读,希望能通过该书建立较为完整的知识体系。先从最为薄弱,但又想尽快提升的数学入手。2018-2-12 20:33
http://begin.lydsy.com/JudgeOnline/problemset.php?page=38
0x31 质数
//4789: Poj2689 Prime Distance
//有个疑问,2-sqrt(R) 数组得开到1.5*2^15 这已超出内存限制了,写到这里,突然发现是自己的问题,想成1.5*10^15
//实际应该是,1.5*2^15 数组不会超出内存限制
//即数组开到sqrt(2^31)=46500即可,归根结底,还是想得多,动手得少
//处理1<<31遇到障碍,
//赋值1<<31 一直是负数,参考http://blog.csdn.net/hiyohu/article/details/52292634此文 由于编译器将1默认为int类型,将1左移31位时超过了int最长位数,编译器给出一个默认值。想要得到理想中的值需将1强制转换成unsigned long long类型。马上进行修改 .
//处理 v2[2147483648],prime2[2147483648]; 发现 溢出了。
//求助网络,此文代码写得比较合心意https://www.cnblogs.com/kuangbin/archive/2013/05/20/3089840.html
//该题要小心,在计算的过程中,int容易溢出,有些地方要注意强转long long
//原题可参考 https://vjudge.net/problem/POJ-2689
//样例通过,提交Wrong Answer if(L<2)L=2;//漏了此句,一直AC ,确实如此,若无此句,按下面算法,1也是质数,当然是错误的
//若无测试数据,思考无果,只能对照正确代码进行排错,提交AC 2018-2-15 9:33
//该题比较核心的思想:任何一个合数n必定包含一个不超过sqrt(n)的质因数。
//额外的知识,每logN个数中大约有1个质数
//该题断续编了有5天之间,思考量,思维量比较大,建议读者自己先编,收获比直接看解答大得多得多。
#include <stdio.h>
#include <string.h>
int v1[46500],prime1[46500/2],v2[1000100],prime2[1000100/2];//N个数里的质数个数接近logN
void getPrime1(int n){//筛法 //获得2--n==sqrt(R)之间的质数
int i,j;
memset(v1,0,sizeof(v1)),prime1[0]=0;//prime1[0]用来统计prime1[]中质数个数
for(i=2;i<=n;i++){
if(v1[i]==0)v1[i]=i,prime1[++prime1[0]]=i;//此处写成v1[i]=2//i是质数
for(j=1;j<=prime1[0];j++){
if(prime1[j]>v1[i]||prime1[j]*i>n)break;//prime1[j]>v[i] i已经用采用最小质数v[i]处理过了,避免重复处理,跳出循环;prime1[j]*i>n 数据已经超出排查范围,跳出循环
v1[i*prime1[j]]=prime1[j];
}
}
}
void getPrime2(int L,int R){//获得L--R之间的质数
int i,j,start;
memset(v2,0,sizeof(v2)),prime2[0]=0;
if(L<2)L=2;//漏了此句,一直AC ,确实如此,若无此句,按下面算法,1也是质数,当然是错误的
for(i=1;i<=prime1[0]&&(long long)prime1[i]*prime1[i]<=R;i++){//请注意(long long)prime1[i]*prime1[i]<=R技巧,prime1[i]*prime1[i]容易超出int范围//i<=prime1[0] 不能超出质数范围, prime1[i]*prime1[i]<=R 不能超出右边界
start=L/prime1[i]+(L%prime1[i]>0);//要求start*prime1[i]i>=L;
if(start==1)start=2;//start必须从2开始 可以参考getPrime1中代码 for(i=2;i<=n;i++) i从2开始
for(j=start;(long long)j*prime1[i]<=R;j++)v2[j*prime1[i]-L]=1;//请注意(long long)j*prime1[i]<=R j*prime1[i]容易超出int范围//此处存在重复,在思考如何处理得更好//请注意 j*prime1[i]-L处理手法,偏移量处理方式,此处 本人 一直未想到,只好参考他人代码,不过还是有收获的
}
for(i=0;i<=R-L;i++)
if(v2[i]==0)prime2[++prime2[0]]=i+L;//此处写成 prime2[++prime2[0]]=i 在进行样例测试中排查出来,注意了,别忘了将偏移量加回去
}
int main(){
int L,R,x1,x2,y1,y2,i;
getPrime1(46500);//46500>sqrt(2^31);
while(scanf("%d%d",&L,&R)!=EOF){
getPrime2(L,R);
if(prime2[0]<2){printf("There are no adjacent primes.\n");continue;}//此处写成break;经样例测试排查出来//区间内质数个数小于两个质数
x1=0,x2=1000100,y1=0,y2=0;
for(i=1;i<prime2[0];i++){//请注意prime2[0]最大值接近log1000000=10*10=100
if(x2-x1>prime2[i+1]-prime2[i])x1=prime2[i],x2=prime2[i+1];
if(y2-y1<prime2[i+1]-prime2[i])y1=prime2[i],y2=prime2[i+1];
}
printf("%d,%d are closest, %d,%d are most distant.\n",x1,x2,y1,y2);//建议字符串直接拷贝输出
}
return 0;
}
若读者觉得意犹未尽,想练练筛法,可以试试下面这道
//P3383 【模板】线性筛素数
//https://www.luogu.org/problemnew/show/P3383 在线测评网站
//2018-2-15 9:57 AC
#include <stdio.h>
#include <string.h>
int v[10000100],prime[10000100/2];
void getPrime(int n){//筛法模板 线性筛法 源自《算法竞赛进阶指南》 时间效率比之前Eratoshenes算法要提高一倍
int i,j;
memset(v,0,sizeof(v)),prime[0]=0;
for(i=2;i<=n;i++){
if(v[i]==0)v[i]=i,prime[++prime[0]]=i;
for(j=1;j<=prime[0];j++){
if(prime[j]>v[i]||prime[j]*i>n)break;
v[i*prime[j]]=prime[j];
}
}
}
int main(){
int n,m,a;
scanf("%d%d",&n,&m);
getPrime(n);
while(m--){
scanf("%d",&a);
if(v[a]==a)printf("Yes\n");
else printf("No\n");
}
return 0;
}
0x32 约数
//4790: Lydsy1053 反素数
//P1463 [HAOI2007]反素数 洛谷https://www.luogu.org/problemnew/show/P1463
//先看题,没看书之前,发现,要筛出1--N中 约数的个数,1<=N<=2,000,000,000 就算是O(n)的算法也要超时
//好吧,先学习书。
//看书学习该题的一系列证明过程,发现真是值回书费,感觉确实内容前后呼应,学习完该章,应能建立一定的数学体系
//https://www.cnblogs.com/zhber/p/4036041.html此文代码写得不错,
//跟踪了上述算法,发现与本人思路正好相反,期待水平提升后,能独立将本人思路编写成功。
//按上述算法编写下来,还是感觉到递归写得不太好
//样例通过,提交AC 2018-2-15 19:36 递归里未必有回溯,回溯里必有递归
#include <stdio.h>
int n,ans=2100000000,mx=0,c[12],prime[]={0,2,3,5,7,11,13,17,19,23,29};//c[i]统计对应prime[i]的个数
void dfs(int pos,int cnt,long long mult){//pos当前质数在prime中的位置,cnt当前约数个数,mult当前对应的约数的乘积
if(mx<cnt||mx==cnt&&ans>mult)mx=cnt,ans=mult;
c[pos]=0;//重置当前位置质数个数
while(mult*prime[pos]<=n&&c[pos]<=c[pos-1]){//请注意c[]是全局变量
c[pos]++,mult*=prime[pos];
dfs(pos+1,cnt*(c[pos]+1),mult);
}
}
int main(){
scanf("%d",&n);
c[0]=32;//质因数幂次和不超过31
dfs(1,1,1);
printf("%d",ans);
return 0;
}
//4791: Lydsy1257 余数之和
//1<=n ,k<=10^9 数据范围,告诉我,要学新知识了
//看书,面强看懂大部分,但还有些细节不清楚,模拟了一堆数据[k/i]*i k从1-11都模拟了一遍,有了写感觉
[1/1]*1=1
[2/1]*1=2
[2/2]*2=2
[3/1]*1=3
[3/2]*2=2
[3/3]*3=3
[4/1]*1=4
[4/2]*2=4
[4/3]*3=3
[4/4]*4=4
[5/1]*1=5
[5/2]*2=4
[5/3]*3=3
[5/4]*4=4
[5/5]*5=5
[6/1]*1=6
[6/2]*2=6
[6/3]*3=6
[6/4]*4=4
[6/5]*5=5
[6/6]*6=6
[7/1]*1=7
[7/2]*2=6
[7/3]*3=6
[7/4]*4=4
[7/5]*5=5
[7/6]*6=6
[7/7]*7=7
[8/1]*1=8
[8/2]*2=8
[8/3]*3=6
[8/4]*4=8
[8/5]*5=5
[8/6]*6=6
[8/7]*7=7
[8/8]*8=8
[9/1]*1=9
[9/2]*2=8
[9/3]*3=9
[9/4]*4=8
[9/5]*5=5
[9/6]*6=6
[9/7]*7=7
[9/8]*8=8
[9/9]*9=9
[10/1]*1=10
[10/2]*2=10
[10/3]*3=9
[10/4]*4=8
[10/5]*5=10
[10/6]*6=6
[10/7]*7=7
[10/8]*8=8
[10/9]*9=9
[10/10]*10=10
[11/1]*1=11
[11/2]*2=10
[11/3]*3=9
[11/4]*4=8
[11/5]*5=10
[11/6]*6=6
[11/7]*7=7
[11/8]*8=8
[11/9]*9=9
[11/10]*10=10
[11/11]*11=11
//参考http://blog.csdn.net/u013598409/article/details/47037031
//参考http://blog.csdn.net/loi_dqs/article/details/50522975根据此文,动手证明了一遍
//摘抄部分:
//添加的证明部分:
//a1=w*L an=w*R 求和S=(a1+an)*(n-1+1)/2
//即S=(w*L+w*R)*(R-L+1)/2 整理可得S=w*(L+R)*(R-L+1)/2
//样例通过,提交AC 2018-2-16 21:37
#include <stdio.h>
typedef long long LL;
int main(){
LL L,R,w,n,k,i,ans;
scanf("%lld%lld",&n,&k);
ans=n*k;
if(n>k)n=k;//k/i i>k k/i=0故 i>k部分对结果无影响,故将n=k
for(i=1;i<=n;i=R+1){
L=i,w=k/i,R=k/w;
if(R>n)R=n;//越界判断
ans-=w*(L+R)*(R-L+1)/2;
}
printf("%lld",ans);
return 0;
}
//4792: Noip2009 Hankson的趣味题
//http://codevs.cn/problem/1172/ 1172 Hankson 的趣味题
//https://www.luogu.org/problemnew/show/P1072洛谷 P1072 Hankson 的趣味题
//http://www.cnblogs.com/cellular-automaton/p/7475678.html此文思路不错,摘抄如下:
//x与a0的最大公约数为a1,那么我们把x/=a1,a0/=a1之后,x和a0不会再有除了1之外的公约数。
//承接上文思路,此文证明不错http://blog.csdn.net/nuclearsubmarines/article/details/77603154
//https://www.luogu.org/problemnew/solution/P1072?&page=4代码写得不错
//样例通过,提交AC 2018-2-17 17:18
#include <stdio.h>
int gcd(int a,int b){
return b?gcd(b,a%b):a;//此处写成 return b?a:gcd(b,a%b); 大失水准,没想到是这里写错,查了好长时间
}
int main(){
int n,a0,a1,b0,b1,i,x,ans;
scanf("%d",&n);
while(n--){
ans=0;
scanf("%d%d%d%d",&a0,&a1,&b0,&b1);
for(i=1;i*i<=b1;i++)
if(b1%i==0){
x=i;
if(x%a1==0&&gcd(x/a1,a0/a1)==1&&gcd(b1/x,b1/b0)==1)ans++;//不写成if(x%a1==0&&gcd(x,a0)==a1&&gcd(x,b0)*b1==x*b0)ans++;原因 x*b0容易超出int范围
x=b1/i;//b1的另一个约数
if(x!=i&&x%a1==0&&gcd(x/a1,a0/a1)==1&&gcd(b1/x,b1/b0)==1)ans++;//不写成if(x!=i&&x%a1==0&&gcd(x,a0)==a1&&gcd(x,b0)*b1==x*b0)ans++;原因 x*b0容易超出int范围
}
printf("%d\n",ans);
}
return 0;
}
//4793: Poj3090 Visible Lattice Points
//https://vjudge.net/problem/POJ-3090可查看该题题目
//首先,为什么是2倍关系,https://yq.aliyun.com/articles/6472此文说得不错,摘抄如下:
//首先ans[1]=3,不经过其他点也就是(x,y)点的gcd(x,y)=1,也就是x,y,互素。所以就是每一行上的个数为phi(n)*2因为行和列都算上就是两倍关系。
//要更深入的了解该题,模拟是少不了的
//size=1 visible points (1,0)(1,1)(0,1)
//size=2 visible points (1,0)(2,1)(1,1)(1,2)(0,1)
//size=3 visible points (1,0)(3,1)(2,1)(3,2)(1,1)(2,3)(1,2)(1,3)(0,1)
//样例通过,提交AC 2018-2-17 22:56
#include <stdio.h>
#include <string.h>
#define maxn 1100
int v[maxn],prime[maxn],phi[maxn];
void Euler(int n){//线性筛法,通质数
int i,j;
memset(v,0,sizeof(v)),prime[0]=0;//prime[0]用来计数质数个数
for(i=2;i<=n;i++){
if(v[i]==0)v[i]=i,prime[++prime[0]]=i,phi[i]=i-1;//i是质数
for(j=1;j<=prime[0];j++){
if(prime[j]>v[i]||prime[j]*i>n)break;//之前已经筛过
v[i*prime[j]]=prime[j];
phi[i*prime[j]]=phi[i]*(i%prime[j]?prime[j]-1:prime[j]);//此处写成 phi[i*prime[j]]=phi[prime[j]]*(i%prime[j]?i-1:i);
}
}
}
int main(){
int c,n,k=0,i,sum;
scanf("%d",&c);
while(c--){
scanf("%d",&n);
Euler(n);
k++,sum=0;
for(i=2;i<=n;i++)sum+=phi[i];
printf("%d %d %d\n",k,n,3+2*sum);
}
return 0;
}
0x33 同余
//4794: The Luckiest Number
//https://vjudge.net/problem/POJ-3696可看原题
//http://blog.csdn.net/qiqijianglu/article/details/7926478此文思路写得不错,摘抄如下:
//思路:这个数一定可以写成11……11*8=(10^0+10^1……+10^(k-1))*8
//化简得8*(10^k-1)/9=mL (等比数列,笔者注)
//-->8*(10^k-1)=9mL
//-->d=gcd(8,L) 8*(10^k-1)/d=9mL/d
//-->p=8/d q=9mL/d p*(10^k-1)=q
//--->因为p,q互质,10^k=1 mod q
//由欧拉定理可知,当q与10互质的时候,10^(phi(q))=1 mod q
//所以无解的时候就是q与10不互质的时候,此外我们求phi(q)的所有因子,按小到大排序,第一个满足10^x =1 mod q的输出。
//上述思路在于,得出 8*(10^k-1)/9=mL 写得不错
//http://blog.csdn.net/wzq_QwQ/article/details/46699751此文让人有阅读学习的兴趣
//http://blog.csdn.net/huanghongxun/article/details/50966715此文代码写得够短,让人有编写的兴趣
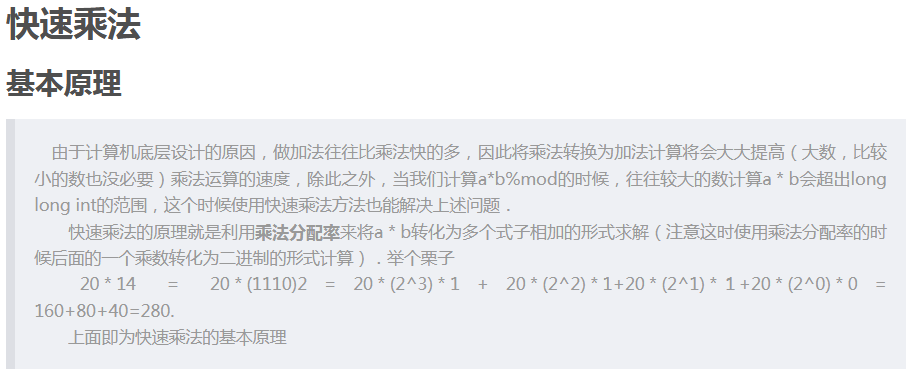
上图公式解释如下:
因8/gcd(8,n)与n/gcd(8,n)互质,因8与9互质,故8/gcd(8,n)与9互质,即gcd(8/gcd(8,n),9)=1,
故8/gcd(8,n)与9*n/gcd(8,n)互质 即gcd(8/gcd(8,n),9n/gcd(8,n))=1
下图公式解释如下:
因8/gcd(8,n)与9*n/gcd(8,n)互质 因(10^x-1)*8/gcd(8,n)=k*9n/gcd(8,n) 故(10^x-1)一定能整除9n/gcd(8,n)
即9n/gcd(8,n)|(10^x-1)
令 q=9n/gcd(8,n)
10^x≡1(mod q)
上述同余关系,来自同余定理 详见 https://baike.baidu.com/item/%E5%90%8C%E4%BD%99%E5%AE%9A%E7%90%86/1212360?fr=aladdin
摘抄如下:
数论中的重要概念。给定一个正整数m,如果两个整数a和b满足a-b能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余,记作a≡b(mod m)。对模m同余是整数的一个等价关系。
用了三天时间,上述证明总算是弄明白了,可以说,没有本书的支持,学到这里很是困难。2018-2-19 19:46
//http://blog.csdn.net/yhrun/article/details/6908470再看此文,发现能看懂了
//在编写快速幂时,提交,一直Wrong Answer ,搜索网络,发现 由于在进行快速幂求模的时候数据会超出long long 的表示范围,因此要进行优化。
//惊呆了,快速幂也会 溢出,马上动手进行验证
//因L(1 ≤ L ≤ 2,000,000,000) f = 9 * L / gcd(8, L); 最大值f时,L=1999999999,最大值f=9*1999999999/1=9*1999999999=17999999991
//故快速幂运算时,模运算参与其中,计算过程中产生的最大值 17999999991*10,000,000,000=1.8*10^20
//而long long 最大值2^63-1=9.2*10^18 unsigned long long 最大值 2^64-1=1.8*10^19
//经过上述一番计算,弄明白了为什么long long 乃至unsigned long long 也会溢出,为学习新知识,做了铺垫
//第一次知道了,快速幂也可以优化。
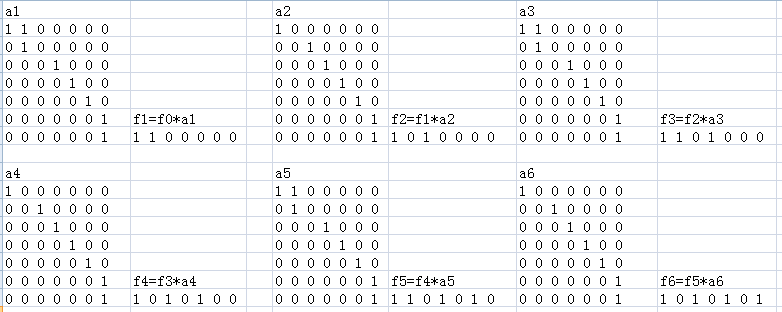
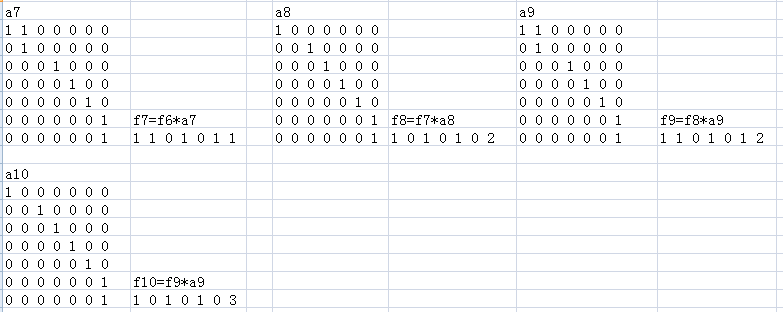
//优化考的是快速乘,马上学习快速乘
//此文快速乘介绍得不错,http://blog.csdn.net/thearcticocean/article/details/50432502摘抄如下:
//此文快速乘介绍得不错,http://blog.csdn.net/u014630623/article/details/50302365 摘抄如下:
//条件具备,可以开始动手编写代码了 2018-2-20 13:23
//该题核心算法:快速排序+欧拉函数+快速幂+快速乘
//约数个数计算,一个正数N的约数上界为2*sqrt(n),欧拉函数最大值,phi[i]=i-1,若i为质数
//故约数个数2*sqrt(17999999991-1)=268329;故约数数组只需开到268400即可,即factor[268400];
//该题所需具备知识:质数,约数,欧几里德算法,欧拉函数,同余,欧拉定理
//编写完毕后,样例未通过,排查,漏洞百出,详见程序,写代码的过程中要十分小心,稍有不慎long long溢出,
//样例通过后,提交,Time Limit Exceed
//对比了该题与 POJ-3696 发现 该题 L(1≤ L ≤ 10^12)而 POJ-3696 L(1 ≤ L ≤ 2,000,000,000) 数据范围竟然改了
//factor范围重新计算,2*sqrt(9*10^12)=2*3*10^6;
//用原书提供的代码提交,Wrong Answer ,那么好,此题作罢,只要POJ-3696上能通过,即可
//推测,该题原文需要修改 与原题 一致,该题数据也需重新修改。该题就此作罢2018-2-20 16:54
#include <stdio.h>
#define LL long long
LL q,factor[268400];
LL gcd(LL a,LL b){//欧几里德算法
return b?gcd(b,a%b):a;//此处写成return b?gcd(b,b%a):a; 欧几里德算法都搞晕了
}
LL phi(LL n){//欧拉函数
LL ans=n,i;
for(i=2;i*i<=n;i++)
if(n%i==0){
ans=ans/i*(i-1);//此处写成 ans=ans*(i-1)/i;计算过程中long long 会溢出
while(n%i==0)n/=i;
}
if(n>1)ans=ans/n*(n-1);//此处写成 ans=ans*(n-1)/n;计算过程中long long 会溢出
return ans;
}
LL quick_mul(LL a,LL b){//快速乘,因快速幂计算过程中,long long 要溢出,采用 快速乘 优化
LL ans=0;
while(b){
if(b&1)ans=(ans+a)%q;
a=(a+a)%q,b>>=1;
}
return ans;
}
LL quick_pow(LL a,LL b){//快速幂
LL ans=1;
while(b){
if(b&1)ans=quick_mul(ans,a);
a=quick_mul(a,a),b>>=1;
}
return ans;
}
void quick_sort(LL left,LL right){//快速排序 ,自小到大排序
LL i=left,j=right,mid=factor[(left+right)/2],t;
while(i<=j){
while(factor[i]<mid)i++;
while(factor[j]>mid)j--;
if(i<=j)t=factor[i],factor[i]=factor[j],factor[j]=t,i++,j--;//i++,j--别忘了,容易漏
}
if(i<right)quick_sort(i,right);
if(left<j)quick_sort(left,j);
}
int main(){
LL x,p,i,flag,kcase=0;
while(scanf("%lld",&x)==1&&x){
q=9*x/gcd(8,x),p=phi(q),factor[0]=0,kcase++,flag=0;//别忘了flag每次都要初始化//factor[0]用来存储约数个数
for(i=1;i*i<=p;i++)//此处写成for(i=2;i*i<=p;i++),混淆进了质数,1也是约数//找p的约数
if(p%i==0){
factor[++factor[0]]=i;
if(p/i!=i)factor[++factor[0]]=p/i;//另一个约数
}
quick_sort(1,factor[0]);
for(i=1;i<=factor[0];i++)
if(quick_pow(10,factor[i])%q==1){//此处写成if(quick_pow(10,i)%q==1)继续有失水准//此处写成 if(quick_pow(10,i)%p==1)有失水准
printf("Case %lld: %lld\n",kcase,factor[i]),flag=1;//此处写成 printf("Case %lld: %lld\n",kcase,i),flag=1;继续有失水准
break;
}
if(flag==0)printf("Case %lld: 0\n",kcase);
}
return 0;
}
//4705: Sumdiv
//https://vjudge.net/problem/POJ-1845可见原题
//该题最大的难点 弄懂 乘法逆元
//概念好懂,推理难懂
//关于费马小定理,此文介绍得不错http://www.xieguofang.cn/Maths/Number_Theory/Fermat's_Little_Theorem_1.htm
//样例通过,提交Wrong Answer; 修改了多出的,和少了的c[prime[0]]++,提交 Wrong Answer
//基本上怀疑,有部分地方int溢出,需强转long long 修改,提交Wrong Answer
//ans=ans*(b%mod*c[i]%mod+1)%mod;//此处写成 ans*=ans*(b%mod*c[i]%mod+1)%mod;多次提交,均未发现 修改 提交Wrong Answer
//提交AC后,还经多次测试,明白了那些地方int 会溢出,收获很大2018-2-21 22:27
#include <stdio.h>
#include <string.h>
#define mod 9901
int prime[10],c[10];
void divide(int n){
int i;
memset(c,0,sizeof(c)),prime[0]=0;//prime[0]存储质因数个数
for(i=2;i*i<=n;i++)
if(n%i==0){
prime[++prime[0]]=i;//此处多了一句 c[prime[0]]++
while(n%i==0)n/=i,c[prime[0]]++;//漏了c[prime[0]]++;
}
if(n>1)prime[++prime[0]]=n,c[prime[0]]++;//特判,本身n就是质数
}
int quick_pow(int a,int b){
int ans=1;
while(b){
if(b&1)ans=ans*a%mod;
a=(a%mod)*(a%mod)%mod,b>>=1;//此句 a=(a%mod)*(a%mod)%mod写得不好的情况,容易int溢出 如 a=(a%mod*a%mod)%mod a=a*a%mod均会溢出
}
return ans;
}
int main(){
int a,b,ans=1,i,x,y;
scanf("%d%d",&a,&b);
divide(a);
for(i=1;i<=prime[0];i++){
if((prime[i]-1)%mod==0){
ans=ans*(b%mod*c[i]%mod+1)%mod;//此处写成 ans*=ans*(b%mod*c[i]%mod+1)%mod;多次提交,均未发现
continue;
}
x=quick_pow(prime[i],b*c[i]+1);//请注意 结果有可能 x=0 这是最不容易发现的地方
x=(x-1+mod)%mod;//最大的Bug 此处写成x=(x-1)%mod; 在计算之前 有可能 x=0//漏了此句 请注意,是等比数列求和之后的 分子 故需 减1
y=quick_pow(prime[i]-1,mod-2);//prime[i]-1的原因是 等比数列,求和公式计算后的分母就是 prime[i]-1 //此处写成 y=quick_pow(prime[i],mod-2);
ans=ans%mod*x%mod*y%mod;
}
printf("%d",ans);
return 0;
}
//4795: Noip2012 同余方程
//http://codevs.cn/problem/1200/可见该题
//https://www.luogu.org/problemnew/show/P1082可见该题
//样例通过,提交AC 2018-2-22 16:05
//http://blog.csdn.net/yoer77/article/details/69568676扩展欧几里德算法,此文介绍得不错,读者可以研读
#include <stdio.h>
int exgcd(int a,int b,int *x,int *y){
int d,t;
if(b==0){
*x=1,*y=0;
return a;
}
d=exgcd(b,a%b,x,y);//此处写成 d=exgcd(a,b,x,y); 确无递推关系
t=*x,*x=*y,*y=t-a/b**y;
return d;
}
int main(){
int a,b,x,y;
scanf("%d%d",&a,&b);
exgcd(a,b,&x,&y);
printf("%d",(x+b)%b);
return 0;
}
//4796: Strange Way to Express Integers
//https://vjudge.net/problem/POJ-2891可见原题
//https://www.cnblogs.com/L-King/p/5721035.html此文代码比较对路
//https://www.cnblogs.com/Missa/archive/2013/06/01/3112536.html
//http://blog.csdn.net/u012294939/article/details/44040091思路摘抄如下(有删改):
//思路,可以参看上述两文,交替研究
//同样是求这个东西。。
//X mod m1=r1
//X mod m2=r2
//...
//...
//...
//X mod mn=rn
//首先,我们看两个式子的情况
//X mod m1=r1……………………………………………………………(1)
//X mod m2=r2……………………………………………………………(2)
//则有
//X=m1*k1+r1………………………………………………………………(*)
//X=m2*k2+r2
//那么 m1*k1+r1=m2*k2+r2
//整理,得
//m1*k1-m2*k2=r2-r1
//令(a,b,x,y,m)=(m1,m2,k1,k2,r2-r1),原式变成
//ax+by=m
//熟悉吧?
//此时,因为GCD(a,b)=1不一定成立,GCD(a,b) | m 也就不一定成立。所以应该先判 若 GCD(a,b) | m 不成立,则!!!方程无解!!!。
//否则,继续往下。
//解出(x0,y0),将k1=x0反代回(*),得到X。即X0%m1=r1,X0%m2=r2
//即X=x0,通解可写成X=x0+m1*k1,X=x0+m2*k2 即(x0+m1*k1)%m1=x0%m1=r1, (x0+m2*k2)%m2=x0%m2=r2
//综合 X=x0+m1*k1,X=x0+m2*k2 可得通解 X=x0+k*LCM(m1,m2) 注LCm(m1,m2)是m1,m2的最小公倍数
//于是X就是这两个方程的一个特解,通解就是 X'=X0+k*LCM(m1,m2)
//这个式子再一变形,得 X' mod LCM(m1,m2)=X0,请注意等号右边是x0
//这个方程一出来,说明我们实现了(1)(2)两个方程的合并。
//令 M=LCM(m1,m2),x0
//就可将合并后的方程记为 X mod M = x0。
//然后,扩展到n个方程。
//用合并后的方程再来和其他的方程按这样的方式进行合并,最后就能只剩下一个方程 X mod M=X0,其中 M=LCM(m1,m2,...,mn)。
//那么,X便是原模线性方程组的一个特解,通解为 X'=X+k*M。
//如果,要得到X的最小正整数解,就还是原来那个方法:
//X%=M;
//if (X<0) X+=M;
//研究下来,发现http://blog.csdn.net/u012294939/article/details/44040091代码更易看懂
//样例通过,提交Wrong Answer
//排查,发现if(f==0)printf("-1\n");//此处写成 printf("0\n"); 真是昏招尽出
//提交AC,2018-2-38 14:03
#include <stdio.h>
#define LL long long
LL exgcd(LL a,LL b,LL *x,LL *y){//每写一次拓展欧几里德算法,就要对该公式进行一次纸上推导
LL d,t;
if(b==0){//结束条件
*x=1,*y=0;
return a;
}
d=exgcd(b,a%b,x,y);
t=*x,*x=*y,*y=t-a/b**y;
return d;
}
int main(){
LL n,a1,r1,a2,r2,x,y,i,f,d,t;
while(scanf("%lld",&n)!=EOF){
f=1;
scanf("%lld%lld",&a1,&r1);
for(i=2;i<=n;i++){
scanf("%lld%lld",&a2,&r2);
if(f==1){
d=exgcd(a1,a2,&x,&y);
if((r2-r1)%d){
f=0;
continue;
}
x=(r2-r1)/d*x,t=a2/d;//此处写成t=a2/(r2-r1)//每次到这里,总要对ax+by=c进行推导
x=(x%t+t)%t;//要求x0>0
r1=a1*x+r1,a1=a1/d*a2;//a1=a1/d*a2 即a1=(a1*a2)/d;
}
}
if(f==0)printf("-1\n");//此处写成 printf("0\n"); 真是昏招尽出
else printf("%lld\n",r1);
}
return 0;
}
0x34 矩阵乘法
//4797: Poj3070 Fibonacci
//https://vjudge.net/problem/POJ-3070可见原题
//原以为,矩阵乘法挺简单,曾经学过,
//没想到有如此妙用,能快速计算该题
//也没想到快速幂还能针对矩阵乘
//真是大开眼界
//样例通过,提交AC 2018-2-23 19:40
#include <stdio.h>
#include <string.h>
#define LL long long
#define m 10000
LL f[2],a[2][2],c1[2],c2[2][2];
void mul(LL f[2],LL a[2][2]){//1*2矩阵 * 2*2矩阵
LL i,j;
memset(c1,0,sizeof(c1));
for(i=0;i<2;i++)
for(j=0;j<2;j++)
c1[i]+=f[j]*a[j][i]%m;//该处i,j如何放置,只要手动能模拟出,就能写出该程序
memcpy(f,c1,sizeof(c1));
}
void mul2(LL a[2][2]){//2*2矩阵 * 2*2矩阵
LL i,j,k;
memset(c2,0,sizeof(c2));
for(i=0;i<2;i++)
for(j=0;j<2;j++)
for(k=0;k<2;k++)
c2[i][j]+=a[i][k]*a[k][j]%m;//同样,该处的i,j,k如何放置,只要手动能模拟出,就能写出该程序
memcpy(a,c2,sizeof(c2));
}
int main(){
LL n;
while(scanf("%lld",&n)&&n!=-1){
f[0]=0,f[1]=1,a[0][0]=0,a[0][1]=1,a[1][0]=1,a[1][1]=1;
if(n==0)printf("0\n");
else if(n==1)printf("1\n");
else{//n>=2
n-=1;
while(n){//快速幂
if(n&1)mul(f,a);
mul2(a);
n>>=1;
}
printf("%lld\n",f[1]%m);
}
}
return 0;
}
//4798: Lydsy2973 石头游戏
//弄不懂样例啊,无奈之下,https://www.cnblogs.com/CQzhangyu/p/6791205.html运行提供的代码,对样例进行测试
//测试过程中,突然明白样例所表达的意思,解释如下
//1 6 10 3 1行6列 6个格子 10秒 3个操作序列
//011112 0格子对应0操作序列,1格子对应1操作序列,2格子对应1操作序列,3格子对应1操作序列,4格子对应1操作序列,2格子对应2操作序列
//1E 0操作序列 第1s 产生1个石头,第2s 对应格子的石头往右移 依次类推
//E 1操作序列 第1s 对应格子的石头往右移 依次类推
//0 2操作序列 第1s 产生0个石头 依次类推
//过程如下
//第1s 0格子里有1个石头
//第2s 0格子里的这个头移到1格
//第3s 0格子里有1个石头,1格里的石头移到2格
//样例总算弄明白了。
//该题陌生度还是比较大,简单看了书中的思路,一句话,都没想到
//对照书中思路,开始编码
//矩阵乘法+快速幂
//为了帮组大家理解上述算法,对样例进行了模拟,过程如下:
//仔细思考,发现该句无法处理,“D:拿走这个格子的石头。”
//https://www.cnblogs.com/CQzhangyu/p/6791205.html再扫一遍里面的代码,发现“D:拿走这个格子的石头。”这句确没处理
//提交上述代码,AC,确实没有处理“D:拿走这个格子的石头。” ,建议该题删去这句“D:拿走这个格子的石头。”,否则该题很难处理
//if('0'<=cmd&&cmd<='9')a[k][num[i][j]][num[i][j]]=1,a[k][0][num[i][j]]=cmd-'0';//程序最难编写的地方//此处写成if('0'<=cmd&&cmd<='9')a[k][0][num[i][j]]=cmd-'0';
//样例通过,提交,Runtime Error
//char s[15][10],c[100];//此处写成c[10] 应是n*m 提交,还是 Runtime Error
//int i,j,k,len,p;//此处写成int i,j,k,len,t; 造成与外面的全局变量t冲突 ,提交,还是 Runtime Error
//多次修改无果,无奈,只好翻出该书提供的测试数据
//看了测试数据后,才发现,“接下来n行,每行m个字符,表示每个格子对应的操作序列。”把n行m列 读成了1行
//修改,提交AC 2018-2-26 20:14 该题编的好久,持续3天。
//提供一组输入数据
//输入:
8 8 390 6
51111112
11111122
41111222
44112222
44403222
44433322
44333332
43333333
000000
00000E
00000S
00000W
00000N
10000E
//输出:
3
#include <stdio.h>
#include <string.h>
#define LL long long
int n,m,t,act,q,r;
int num[10][10];//num[i][j]对应格子位置,
LL f[100],a[100][100][100],d[100][100],b[100];//f[num[i][j]]记录格子(i,j)中石头个数
char s[15][10],c[10][10]; //此处写成c[100]//此处写成c[10] 应是n*m
void push(int i,int j,int k,char cmd){//产生石头 ,以及 往四周推 石头
if('0'<=cmd&&cmd<='9')a[k][num[i][j]][num[i][j]]=1,a[k][0][num[i][j]]=cmd-'0';//程序最难编写的地方//此处写成if('0'<=cmd&&cmd<='9')a[k][0][num[i][j]]=cmd-'0';
else if(cmd=='N'&&i>1)a[k][num[i][j]][num[i-1][j]]=1;
else if(cmd=='S'&&i<n)a[k][num[i][j]][num[i+1][j]]=1;
else if(cmd=='W'&&j>1)a[k][num[i][j]][num[i][j-1]]=1;
else if(cmd=='E'&&j<m)a[k][num[i][j]][num[i][j+1]]=1;
}
void mul(LL a[100][100],LL b[100][100]){//矩阵乘法
int i,j,k;
memset(d,0,sizeof(d));
for(i=0;i<=n*m;i++)
for(j=0;j<=n*m;j++)
for(k=0;k<=n*m;k++)
d[i][j]+=a[i][k]*b[k][j];
memcpy(a,d,sizeof(d));
}
void mul2(LL f[100],LL a[100][100]){//矩阵乘法
int i,j;
memset(b,0,sizeof(b));
for(i=0;i<=n*m;i++)
for(j=0;j<=n*m;j++)
b[i]+=f[j]*a[j][i];
memcpy(f,b,sizeof(b));
}
void quick_pow(LL a[100][100],LL b[100][100],int q){//快速幂
while(q){
if(q&1)mul(b,a);
mul(a,a),q>>=1;
}
}
int main(){
int i,j,k,len,p;//此处写成int i,j,k,len,t; 造成与外面的全局变量t冲突//t=q*60+r
LL max=-1;
memset(f,0,sizeof(f)),f[0]=1;//f[i]状态矩阵
memset(a,0,sizeof(a)),a[0][0][0]=1;//a[i][j]转移矩阵
scanf("%d%d%d%d",&n,&m,&t,&act);
for(i=1;i<=n;i++)scanf("%s",c[i]);//此处写成scanf("%s",c);
for(i=0;i<act;i++)scanf("%s",s[i]);
q=t/60,r=t%60;
for(i=1;i<=n;i++)//行
for(j=1;j<=m;j++)//列
num[i][j]=(i-1)*m+j;//二维化一维
for(k=1;k<=60;k++){//经测试无误//60是1-6的最小公倍数 处理a1-a60 转移矩阵
a[k][0][0]=1;//该位置产生石头
for(i=1;i<=n;i++)
for(j=1;j<=m;j++){
p=c[i][j-1]-'0';//此处写成t=c[num[i][j]]-'0';//(i,j)格子对应的操作序列
len=strlen(s[p]);
push(i,j,k,s[p][(k-1)%len]);//此处写成 for(p=0;p<len;p++)push(i,j,k,s[t][p]);
}
}
memcpy(a[61],a[1],sizeof(a[1]));//a[61] 用来存储ar转移矩阵
for(k=2;k<=r;k++)mul(a[61],a[k]);//计算ar转移矩阵
memcpy(a[62],a[61],sizeof(a[61]));//a[62] 用来存储a60转移矩阵
for(k=r+1;k<=60;k++)mul(a[62],a[k]);//此处写成for(k=r+1;k<=60;k++)mul(a[61],a[k]);昏招//计算a60转移矩阵
for(i=0;i<=n*m;i++)//将a[63]初始化为单位矩阵
for(j=0;j<=n*m;j++)
if(i==j)a[63][i][j]=1;
quick_pow(a[62],a[63],q);//a[63]用来存储(a60)^q
mul2(f,a[63]);
mul2(f,a[61]);
for(i=1;i<=n*m;i++)
if(max<f[i])max=f[i];
printf("%lld",max);
return 0;
}
0x35 高斯消元法与线性空间
//球形空间产生器BZOJ1013
//http://www.lydsy.com/JudgeOnline/problem.php?id=1013可见原题
//https://www.luogu.org/problemnew/show/P4035可见原题
//解释一下,为什么要提供n+1组数据,圆心坐标x1,x2,...,xn-1,xn,有n个未知数,半径R也是一个未知数,未知数共计n+1个,需要n+1个方程,故需提供n+1组数据
//对样例进行推演
//(a11-x1)^2+(a12-x2)^2=R^2 (1) a11表述数据1在1维度上的坐标值,a12表述数据1在2维度上的坐标值
//(a21-x1)^2+(a22-x2)^2=R^2 (2) a21表述数据2在1维度上的坐标值,a22表述数据2在2维度上的坐标值
//(a31-x1)^2+(a32-x2)^2=R^2 (3) a31表述数据3在1维度上的坐标值,a32表述数据3在2维度上的坐标值
//将(2)-(1)可得 2*(a11-a21)*x1+2*(a12-a22)*x2=a11^2-a21^2+a12^2-a22^2
//将(3)-(2)可得 2*(a21-a31)*x1+2*(a22-a32)*x2=a21^2-a31^2+a22^2-a32^2
//上述样例推演目的,方便读者看懂书中通式
//惊呆了,样例一次性通过,洛谷里 提交,一次性AC。2018-2-27 22:35
//还是那句话,会算,编起来就容易多了
#include <stdio.h>
#include <string.h>
#include <math.h>
double a[15][15],b[15],c[15][15];
void swap(double a,double b){
double t;
t=a,a=b,b=t;
}
int main(){
int i,j,k,n;
double rate;
memset(b,0,sizeof(b));
scanf("%d",&n);
for(i=1;i<=n+1;i++)//数据读取
for(j=1;j<=n;j++)
scanf("%lf",&a[i][j]);
for(i=1;i<=n;i++)//转化为 行列式
for(j=1;j<=n;j++)
c[i][j]=2*(a[i][j]-a[i+1][j]),b[i]+=a[i][j]*a[i][j]-a[i+1][j]*a[i+1][j];
for(i=1;i<=n;i++){//i表示矩阵的列//高斯消元
for(j=i;j<=n;j++){//该功能保证当前的x[i]系数非零//j表示矩阵的行
if(fabs(c[j][i])>1e-8){//保证x[i]系数非零//非零
for(k=1;k<=n;k++)swap(c[i][k],c[j][k]);
swap(b[i],b[j]);
}
}
for(j=1;j<=n;j++){//所有的行//目标:除了对角线外,其他列处的系数为0
if(j==i)continue;//避免出现自己-自己 的情况
rate=c[j][i]/c[i][i];
for(k=1;k<=n;k++)c[j][k]-=c[i][k]*rate;//每行的数据
b[j]-=b[i]*rate;
}
}
printf("%.3lf",b[1]/c[1][1]);
for(i=2;i<=n;i++)printf(" %.3lf",b[i]/c[i][i]);//打印
return 0;
}
//4800: Poj1830 开关问题
//https://vjudge.net/problem/POJ-1830可见原题
//开关,容易与二进制搭上关系
//0 < N < 29 ,故0 < N+1 < 30 int有31位,极限情况int还是不会溢出
//样例通过,提交Wrong Answer
//ans=1;//漏了此句,if(a[i]==1),if(a[i]==0)均未进入,即自由元0个,2^0=1答案为1 ,因为此句,一直Wrong Answer
//提交AC,2018-3-1 14:51
#include <stdio.h>
int a[40];
int main(){
int i,j,k,t,n,x,y,ans,b;
scanf("%d",&t);
while(t--){
ans=1;//漏了此句,if(a[i]==1),if(a[i]==0)均未进入,即自由元0个,2^0=1答案为1 ,因为此句,一直Wrong Answer
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
for(i=1;i<=n;i++){
scanf("%d",&j);
a[i]^=j,a[i]|=1<<i;//处理第0位,第i位
}
while(~scanf("%d%d",&x,&y)&&x&&y)a[y]|=1<<x;
for(i=1;i<=n;i++){
for(j=i+1;j<=n;j++)//此处写成for(j=i+1;j<=n;i++)笔误害人//类冒泡排序
if(a[i]<a[j])//自大到小排序,即找出最高位
b=a[i],a[i]=a[j],a[j]=b;//此处写成 t=a[i],a[i]=a[j],a[j]=t;请注意t已被 数据组数所占用
if(a[i]==1){ans=0;break;}//即 0001 无解
if(a[i]==0){ans=1<<n-(i-1);break;}//即a[i]==0,a[i+1]==0,...,a[n]==0 0000 即i ,i+1,...,n均是自由元
for(k=n;k>=1;k--)//高斯消元
if(a[i]>>k&1){//找到最高位为1
for(j=1;j<=n;j++)//削掉第k位
if(j!=i&&a[j]>>k&1)a[j]^=a[i];//该行if(j!=i&&a[j]>>k&1)中的a[j]>>k&1翻书才想起
break;
}
}
if(ans==0)printf("Oh,it's impossible~!!\n");
else printf("%d\n",ans);
}
return 0;
}
//4801: Lydsy4004 装备购买
//https://www.luogu.org/problemnew/show/P3265可见该题,网络中的代码在此处大都能AC
//http://begin.lydsy.com/JudgeOnline/problemstatus.php?id=4801这里的数据更苛刻,好还是不好呢?
//向量需要高中数学的基础,本质,就是用坐标系表示
//没什么经验,对 秩 感到陌生,弄个代码能AC的代码来研究https://www.cnblogs.com/SilverNebula/p/6353939.html
//贪心+高斯消元
//为了方便读者理解,样例模拟如下:
//经过一番折腾,发现加入long double 之后,Dev-C++4.9.9.2已无跟踪,编译能力,研究的过程瞎子摸象
//建议编写时,这样操作,先用double,在Dev-c++4.9.9.2进行跟踪研究,没有问题后,将double改成long double
//样例通过,终于提交AC,2018-3-2 16:29
//若采用C++方式提交,可用fabs,fabsl,若采用C方式提交,采用fabsl
#include <stdio.h>
#include <string.h>
#include <math.h>
#define double long double//此处写成 #define long double double
#define maxn 510
#define eps 1e-7
struct node{//用结构体的目的是方便排序
double b[maxn];
int w;
}a[maxn],a_t,p[maxn];
int vis[maxn];
void quicksort(int left,int right){//快排,按w自小到大排序
int i=left,j=right,mid=a[(left+right)/2].w;//没想到快排也会写错,此处写成 int i,j,mid=a[(left+right)/2].w;
while(i<=j){
while(a[i].w<mid)i++;
while(a[j].w>mid)j--;
if(i<=j)a_t=a[i],a[i]=a[j],a[j]=a_t,i++,j--;
}
if(i<right)quicksort(i,right);
if(left<j)quicksort(left,j);
}
int main(){
int n,m,i,j,k,cnt=0,cost=0;
double rate;
memset(vis,0,sizeof(vis));
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
scanf("%Lf",&a[i].b[j]);//请注意long double 必须%Ld L必须大写
for(i=1;i<=n;i++)scanf("%d",&a[i].w);
quicksort(1,n);
for(i=1;i<=n;i++)//高斯消元
for(j=1;j<=m;j++)
if(fabsl(a[i].b[j])>=eps)//排查了math.h文件,发现extern long double __cdecl fabsl (long double x);//此处写成if(fabs(a[i].b[j])>eps) C里面有问题//此处写成if(a[i].b[j]>eps)//大于0
if(vis[j]==0){//该列元素未被访问
vis[j]=1,p[j]=a[i],cnt++,cost+=p[j].w;
break;//漏了此句
}
else{
rate=a[i].b[j]/p[j].b[j];
for(k=1;k<=m;k++)a[i].b[k]-=rate*p[j].b[k];//此处写成a[i].b[k]-=rate*p[i].b[k];
}
printf("%d %d\n",cnt,cost);
return 0;
}
//4802: Hdu3949 XOR
//http://acm.hdu.edu.cn/showproblem.php?pid=3949可见该题
//https://vjudge.net/problem/HDU-3949可见该题
//提交,Compilation Error,发现全是在有注释的地方,注释竟然不行,
//删除注释,提交Wrong Answer,仔细想了想,zero=0应在每组数据开始 int t,n,zero; //此处写成 int t,n,zero=0;
//修改,提交 Wrong Answer,排查代码,发现if(a[i]==0){t=i-1;zero=1;break}//此处写成 if(a[i]==0)t=i-1,zero=1;
//修改,提交Wrong Answer,对照代码才发现,本应是unsigned long long k写成int ,题目没读全,修改,提交AC 2018-3-3 12:28
//if(zero)k--;原因是,利用异或得不到0,最小值0必须从ans=0的初始值中得到,故必须k--
#include <stdio.h>
#define maxn 10100
#define ULL unsigned long long
ULL a[maxn],b;
int t,n,zero;
void gauss(){
int i,j,k;
for(i=1;i<=n;i++){
for(j=i+1;j<=n;j++)
if(a[i]<a[j])b=a[i],a[i]=a[j],a[j]=b;
if(a[i]==0){t=i-1;zero=1;break;}
for(k=63;k>=0;k--)
if(a[i]>>k&1){
for(j=1;j<=n;j++)
if(j!=i&&a[j]>>k&1)
a[j]^=a[i];
break;
}
}
}
int main(){
ULL ans,k;
int T,q,i,j,kase=0;
scanf("%d",&T);
while(T--){
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%llu",&a[i]);
t=n,zero=0;
gauss();
scanf("%d",&q);
kase++;
printf("Case #%d:\n",kase);
while(q--){
ans=0;
scanf("%llu",&k);
if(zero)k--;
if(k>=1ULL<<t){printf("-1\n");continue;}
for(i=t-1;i>=0;i--)
if(k>>i&1)ans^=a[t-i];
printf("%llu\n",ans);
}
}
return 0;
}
0x36 组合计数
//4803: Noip2011 计算系数
//http://codevs.cn/problem/1137/可见该题
//https://www.luogu.org/problemnew/show/P1313可见该题
//由杨辉三角可得:C(k,n)=C(k-1,n-1)+c(k-1,n) 初始值C(k,0)=1,C(k,k)=1
//因存在int溢出风险,故全采用long long
//样例通过,提交AC 2018-3-3 21:28
//方法二:快速幂+逆元
//参考了https://www.luogu.org/problemnew/solution/P1313?&page=3写法,看来逆元需要好好复习2018-3-3 21:46
#include <stdio.h>
#define mod 10007
#define LL long long
LL quick_pow(LL a,LL n){//快速幂
LL ans=1;
while(n){
if(n&1)ans=(ans*a)%mod;
a=(a*a)%mod;
n>>=1;
}
return ans;
}
int main(){
LL a,b,k,n,m,i,j,c=1,d=1;
scanf("%lld%lld%lld%lld%lld",&a,&b,&k,&n,&m);
for(i=1;i<=n;i++)c=c*i%mod;
for(i=k-n+1;i<=k;i++)d=d*i%mod;
d=d*quick_pow(c,mod-2)%mod;
printf("%lld",d*quick_pow(a,n)*quick_pow(b,m)%mod);
return 0;
}
//4803: Noip2011 计算系数
//http://codevs.cn/problem/1137/可见该题
//https://www.luogu.org/problemnew/show/P1313可见该题
//由杨辉三角可得:C(k,n)=C(k-1,n-1)+c(k-1,n) 初始值C(k,0)=1,C(k,k)=1
//因存在int溢出风险,故全采用long long
//样例通过,提交AC 2018-3-3 21:28
#include <stdio.h>
#define mod 10007
#define LL long long
LL c[1010][1010];
LL quick_pow(LL a,LL n){//快速幂
LL ans=1;
while(n){
if(n&1)ans=(ans*a)%mod;
a=(a*a)%mod;
n>>=1;
}
return ans;
}
int main(){
LL a,b,k,n,m,i,j;
scanf("%lld%lld%lld%lld%lld",&a,&b,&k,&n,&m);
for(i=1;i<=k;i++)c[i][0]=1;
for(i=1;i<=k;i++)c[i][i]=1;
for(i=2;i<=k;i++)
for(j=1;j<i;j++)
c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
printf("%lld",(c[k][n]*quick_pow(a,n)*quick_pow(b,m))%mod);
return 0;
}
多重集合的组合数 可通过 https://blog.csdn.net/mrcrack/article/details/80562324 第10讲内容 内容进行 学习。2018-9-8 19:07
多重集的组合数:http://blog.csdn.net/kennyrose/article/details/7469528此文介绍得相当棒,摘抄其中一个例子如下:
例1:线性方程 x1 + x2 + ... + xk = r 一共有多少组非负整数解?
解答:上述不定方程的非负整数解对应于下述排列
1...101...1 01...1 0 ...... 01...1
x1 个 x2 个 x3 个 ...... xk 个
其中 k-1个 0 将 r 个 1 分成k段, 每段含1的个数分别为 x1, x2, ..., xk,
很明显这个排列是多重集合 S = { r * 1, (k-1)* 0 }的全排列
即:P(r+k-1; r*1, (k-1)*0) = (r+k-1)! / ( r! * (k-1)! ) = C( r+k-1, r),即从k类元素中选r个的种类
2018-3-9 22:08
//4804: Counting Swaps
//https://ipsc.ksp.sk/2016/real/problems/c.html可见该题
//因无处提交代码,此题暂时搁置。2018-3-5
//4805: Lydsy1951 古代猪文
//http://codevs.cn/problem/1830/可见该题
//https://www.luogu.org/problemnew/show/P2480可见该题
//样例模拟如下
//N=4,q=2,d|N d=1,4,2
//C(4,1)=4,C(4,2)=6,C(4,4)=1 和为11
//2^11=2048
//https://www.cnblogs.com/wuminyan/p/5188551.html此文代码写得不错,可以参考一下
//光看他人源代码,就花了很长时间,有3天之多,感受是思维提升了,很多数论问题有了更深的体会。
//乘法逆元+卢卡斯定理+拓展欧几里得算法+中国剩余定理+快速幂
//为尽可能的避免数据溢出,采用long long
//该题对数论要求比较高,要想编码成功,需要对数论比较清晰。样例通过,提交AC 2018-3-9
//该题耗时五天之久,收获就是数论有些感觉。
#include <stdio.h>
#define LL long long
#define mod 999911659
LL n,g,fact[4][35700],prime[4]={2,3,4679,35617},b[4];//此处写成fact[35700]//fact阶乘 prime[] 2*3*4679*35617=999911658
LL quick_pow(LL a,LL b,LL x){
LL ans=1;
while(b){
if(b&1)ans=ans*a%x;
a=a*a%x,b>>=1;
}
return ans;
}
LL Comb(LL n,LL m,LL i){//组合数计算
if(n<m)return 0;//为了程序的健壮性写的
return fact[i][n]*quick_pow(fact[i][n-m]*fact[i][m],prime[i]-2,prime[i])%prime[i];//此处写成fact[i][n]*quick_pow(fact[i][n-m]*fact[i][m],prime[i]-2,i)%prime[i];//乘法逆元
}
LL lucas(LL n,LL m,LL i){
if(m==0)return 1;
return Comb(n%prime[i],m%prime[i],i)*lucas(n/prime[i],m/prime[i],i)%prime[i];
}
LL exgcd(LL a,LL b,LL *x,LL *y){
LL t,d;
if(b==0){
*x=1,*y=0;
return a;
}
d=exgcd(b,a%b,x,y);//此处写成 d=exgcd(a,b,x,y);
t=*x,*x=*y,*y=t-a/b**y;
return d;
}
LL CRT(){//中国剩余定理
LL N=1,i,j,m,ans=0,x,y;
for(i=0;i<4;i++)N*=prime[i];
for(i=0;i<4;i++){
m=N/prime[i];
exgcd(m,prime[i],&x,&y);
ans=(ans+x*m*b[i])%N;//此处写成ans=(ans+x*m*b[i])%mod;,查了好长时间
}
ans=(ans%N+N)%N;//此处写成ans=(ans%mod+N)%mod;,查了好长时间 //保证ans最后结果>0
return ans;
}
int main(){
LL i,j,k;
scanf("%lld%lld",&n,&g);
if(g==mod){
printf("0");
return 0;
}
g%=mod;
for(i=0;i<4;i++){
fact[i][0]=1;
for(j=1;j<=prime[i];j++)
fact[i][j]=fact[i][j-1]*j%prime[i];//此处写成fact[i][j]=fact[i][j-1]*j%mod;//fact[i]=i!阶乘计算
}
for(i=1;i*i<=n;i++)//找n的约数
if(n%i==0){
k=n/i;
for(j=0;j<4;j++){
if(k!=i)b[j]=(b[j]+lucas(n,k,j))%prime[j];
b[j]=(b[j]+lucas(n,i,j))%prime[j];
}
}
printf("%lld",quick_pow(g,CRT(),mod)%mod);
return 0;
}
0x37 容斥原理与Mobius函数
容斥原理,多重集的组合数,可看https://blog.csdn.net/mrcrack/article/details/80562324 第17讲内容 例子 10组合,定能弄明白书中公式的意义。2018-9-8 20:14
没有接触过容斥原理,可以看看这篇文章http://www.sohu.com/a/198865515_128501先有一个基本印象。2018-3-10 10:21
关于多重集,此文介绍得相当棒https://blog.csdn.net/kennyrose/article/details/7469528摘抄部分内容如下 2018-4-20
例1:线性方程 x1 + x2 + ... + xk = r 一共有多少组非负整数解?
解答:上述不定方程的非负整数解对应于下述排列
1...101...1 01...1 0 ...... 01...1
x1 个 x2 个 x3 个 ...... xk 个
其中 k-1个 0 将 r 个 1 分成k段, 每段含1的个数分别为 x1, x2, ..., xk,
很明显这个排列是多重集合 S = { r * 1, (k-1)* 0 }的全排列
即:P(r+k-1; r*1, (k-1)*0) = (r+k-1)! / ( r! * (k-1)! ) = C( r+k-1, r),即从k类元素中选r个的种类
多重集的理解,借助上例,很快就能理解。
多重集的例题,此文不错,可以学习研究https://blog.csdn.net/thearcticocean/article/details/46794101
例题 Devu and Flowers 在线测评可见 https://vjudge.net/problem/CodeForces-451E
试着推导 多重集的组合数公式,竟然成功了,方法一是从 公式角度入手,方法二是从组合的意义入手,全部成功。虽然有些磕碰,但时隔这么久,能成功,证明是掌握了。2018-9-9 16:15
根据容斥原理,将样例全部算了一遍,数据全部对上,可以开始考虑编码了。2018-9-9 16:36
看了数据范围,long long是省不了了,有顾虑,算组合数,十有八九要溢出。2018-9-9 16:48
还有一个疑惑,容斥原理如何结束。2018-9-9 17:05
//https://vjudge.net/problem/CodeForces-451E
//Devu and Flowers
//参考了书中代码,但没有照抄。
//编好一个函数,测试一个函数
//2018-9-11
//t-=p;//此处写成t-=(p+1); 这是编码中最核心的错误,大约花了30分钟排错 主要靠printf 才找到错误
//3个样例均通过,提交AC。2018-9-11
//该程序的原理,多重集的组合+容斥原理 的学习,致使该代码的诞生足足延迟了半年。
#include <stdio.h>
#define LL long long
#define mod 1000000007
LL inv[25];//逆元
LL myPower(LL a,LL b){//a^b 快速幂 可采用2^10模拟 来编写该代码。
LL c=1;
while(b){
if(b&1)//判断b是奇数
c=c*a%mod;
a=a*a%mod;
b>>=1;
}
return c;
}
LL comb(LL y,LL x){//c(y,x) 想一想C(5,2)计算,该函数很快就能编出。
LL c=1,i;
if(y<0||y<x||x<0)return 0;
if(x==0||y==x)return 1;
y%=mod;
for(i=0;i<x;i++)c=c*(y-i)%mod;
for(i=x;i>=1;i--)c=c*inv[i]%mod;//变除法为乘法 逆元
return c;
}
int main(){
LL i,a[25],n,s,ans,p,t,x;
for(i=1;i<=20;i++)inv[i]=myPower(i,mod-2);//计算i的逆元
scanf("%lld%lld",&n,&s);
for(i=1;i<=n;i++)scanf("%lld",&a[i]);
for(x=0;x<1<<n;x++){//二进制 每位对应一个集合的使用 多重集的组合+容斥原理 该循环,测试了x的值,一次性成功。
p=0;
t=n+s;
if(x==0)ans=comb(t-1,n-1);
else{
for(i=0;i<n;i++)//查找n次,因有n位
if(x>>i&1){
p++;
t-=a[i+1];
}
t-=p;//此处写成t-=(p+1); 这是编码中最核心的错误,大约花了30分钟排错 主要靠printf 才找到错误//之前的问题 将该代码块 放在了 else之外。
if(p&1){//奇数 -
ans=(ans-comb(t-1,n-1))%mod;
}else{//偶数 +
ans=(ans+comb(t-1,n-1))%mod;
}
}
}
printf("%lld\n",(ans+mod)%mod);
}
0x38 概率与数学期望
0x39 0/1分数规划
0x3A 博弈论之SG函数
0x3B 总结与练习































 2176
2176

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








