数据结构与算法分析之伸展树(splaytree)

伸展树定义

伸展树是在查询或删除时对二叉查找树进行伸展操作，并保证从空树开始任意连续M次对树的操作最多花费O(MlogN)的时间。

对二叉查找树进行伸展的意义是将访问路径上的节点尽可能的推向离树根最近的地方，有益于在下次访问时用时最少。通常一个节点被访问时，很可能不久会被再次访问。

如何构造一个伸展树?

方法1：

访问到X节点时，从X处通过单旋转将X移动到根节点处，也就是将访问路径上的每个节点和他们的父节点都实施旋转。这种旋转的效果是将访问节点X一直推向树根，但是不好的地方是可能将其他节点推向更深的位置。这种效果并不好，因为它没有改变访问路径上其他节点的后序访问状况。

方法2：

和方法1类似，在访问节点X时，根据X节点和其父节点(P)以及祖父节点(G)之间的形状做相应的单旋转或者双旋转。如果三个节点构成LR或RL时(即之字形)，则进行相应的双旋转；如果构成LL或者RR时进行对应的单旋转(一字型)。这样展开的效果是将X推向跟节点的同时，访问路径上其他节点的深度大致都减小了一半(某些浅的节点最多向退后了两层)。这有做对绝大多数访问路径上的节点的后序访问都是有益的。

伸展树的基本特性

当访问路径太长而导致超出正常查找时间的时候，这些旋转将对未来的操作(下一次访问)有益；当访问耗时很少的时候，这些旋转则不那么有益甚至有害。

伸展树的伸展操作

伸展树的伸展方式有两种，一种是自下向上的伸展；另一种是自上向下的伸展。比较容易理解的是自下向上的伸展，我们会重点解释自顶向下的实现方式。

自低向上的伸展

先自顶向下搜寻X节点，当搜索到X节点时，从X节点开始到根节点的路径上所有的节点进行旋转，最终将X节点推向跟节点，将访问路径上的大部分节点的深度都降低。

具体旋转需要根据不同的情形进行，在X节点处有三种情形需要考虑(假设X的父节点为P，X的祖父节点为G)：

1.X的父节点P就是树根的情形，这种情形比较简单，只需要将X和P进行旋转即可，X和P构成LL就左单旋转，构成RR就右单旋转

2.X和P和G之间构成之字型的情形，即LR和RL类型。如果是LR则进行左双旋转，如果是RL进行右双旋转。如下图所示

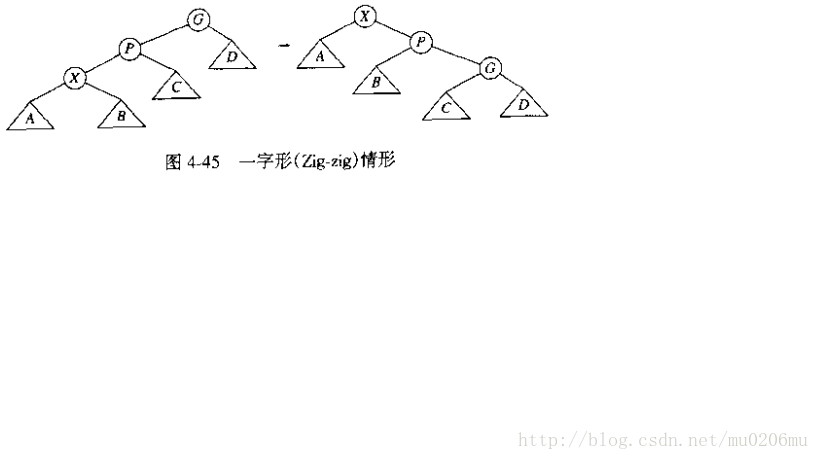
3.X和P和G之间构成一字型的情形，即LL和RR类型。如果是LL则执行两次单左旋转，如果是RR则执行两次单右旋转。如下图所示：

自低向上的实现：

/*
 * down-top
 * 自下向上的方式一般都不推荐使用，首先效率不高，需要在访问路径上两次遍历。
 * 一次是先向下遍历找到X节点，另一次是从X节点向上移动到根节点处；
 * 另外一个考虑是节点中需要一个额外的指针用来保存父亲节点
 * */
static SplayTree Splay(Position X, SplayTree T)
{
	Position P, G;

	P = X->Parent;
	while(P != NULL) {
		G = P->Parent;
		/* X是P的左儿子 */
		if (X == P->Left) {
			if (G == NULL)
				SingleRotateWithLeft(P);
			else if (P == G->Left) {//LL类型
				SingleRotateWithLeft(P);/* X P左单旋 */
				SingleRotateWithLeft(G);/* X G左单旋 */
			} else
				DoubleRotateWithRight(G);/* RL型 */
		} else {
		/* X是P的右儿子 */
			if (G == NULL)
				SingleRotateWithRight(P);
			else if (P == G->Right) {//RR
				SingleRotateWithRight(P);/* X P右单旋*/
				SingleRotateWithRight(G);/* X G右单旋 */
			} else
				DoubleRotateWithLeft(G);//LR
		}

		P = X->Parent;// X P G通过一次循环后X已被移动到循环前的G处
	}
	return X;
}

自顶向下的伸展

此种方式的伸展是自顶向下，边查询边旋转，在访问路径上的一次遍历就可完成，效率上要比自低向上的方式高。要想在访问路径上一次遍历并完成伸展，

需要开辟额外子树用于保存遍历过程中的信息。具体操作过程是(假设查找节点X)：

1.先建立两个空子树，一个是LeftTreeMax(简称LTMax)，另一个是RightTreeMin(简称RTMin)。

其中LTMax子树保存遍历过程中所有小于X的节点，并且LTMax在遍历过程中始终指向该子树中最大的那个节点。不难看出LTMax->Right始终为空

RTMin子树保存遍历过程中所有大于X的节点，RTMin在遍历过程中始终指向该子树中最小的那个节点。同样RTMin->Left也始终为空。

因此在合并RTMin和LTMax前，RTMin是所在子树上所有大于X节点中那个最小的并接近X的节点，同理LTMax中所在子树中所有小于X节点中那个最大的并接近X的节点

2.从根节点T开始遍历，查找X节点，直到找到或者未找到

1.0如果X节点小于T并且小于T->Left(LL型)则实行一次围绕T的左单旋转，之后T->Left成为新的根节点T'，X<T'，所以从T‘劈开的右子树(包括T')上的所有节点都大于X，我们将T'挂在RTMin->Left上，并更新RTMin指向T'节点，T‘节点是所有大于X节点中最小的那个。

1.1如果X节点小于T，但T->Left为NULL，则未找到X节点，退出循环并将三个子树合并

2.0如果X节点大于T并且大于T->Right(RR型)，则实行一次围绕T的右单旋转，这样T->Right成为新的根节点T'，X又大于T'，所以从T'劈开的左子树(包括T')上所有的节点都小于X，我们将T’子树挂在LTMax->Right上，并将LTMax指向新的T‘节点，T’节点就是所有小于X节点中最大的那个。

2.1如果X节点大于T，但T-Right为NULL,则未找到X节点，退出循环将三个子树合并

3.当找到或者未找到X节点退出循环后，合并三个子树。

此时LTMax是所有小于X节点的最大的那个，所以要将中子树(简称为M)的M->Left挂在LTMax->Right上，将M->Right挂在RTMin->Left上。最后更新M为LTMax和RTMin的根节点。

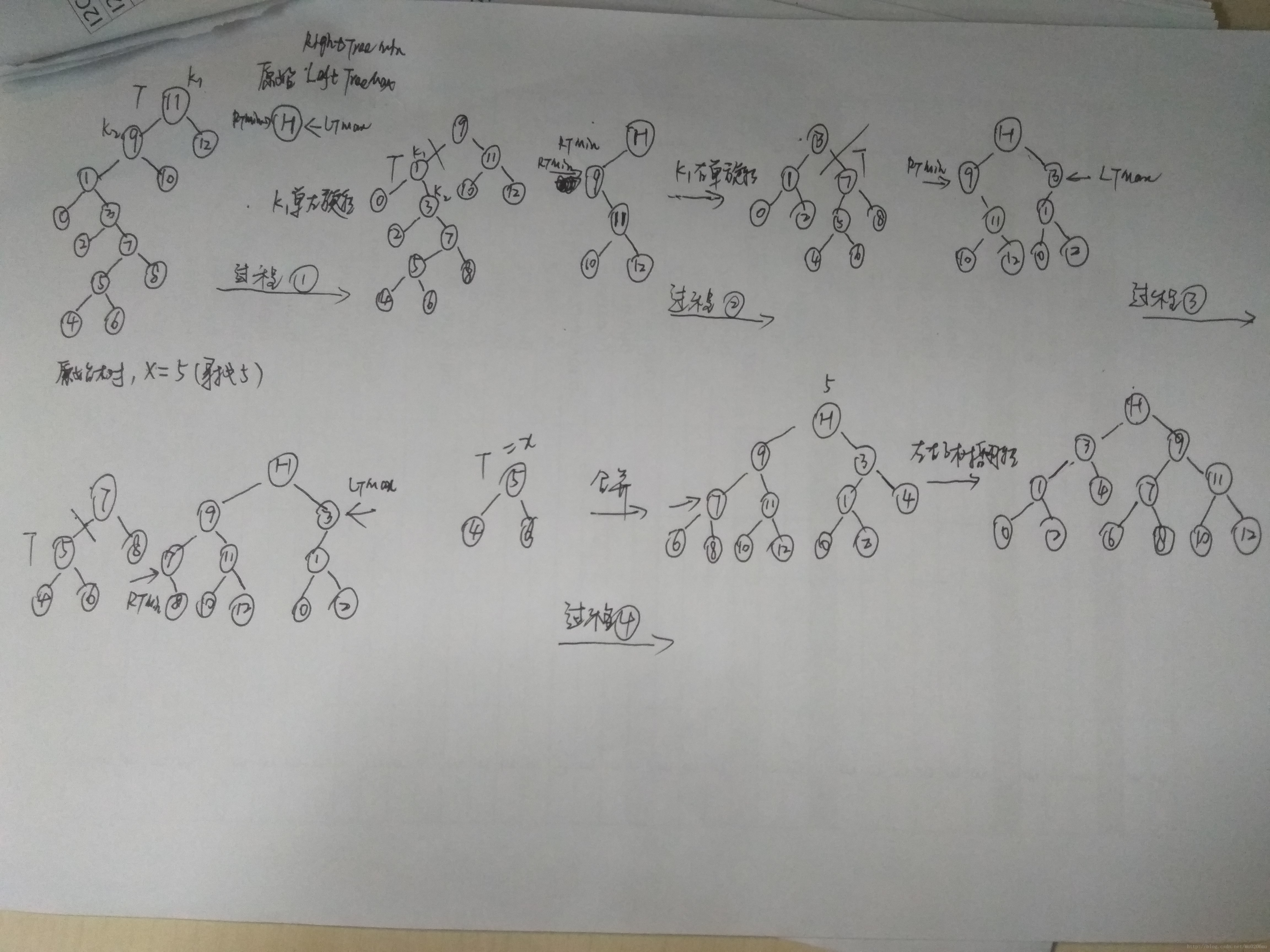
文字描述太过抽象，下面看一个例子，如下图所示：

假设寻找X=5的节点

过程1：

X小于根节点11，同时还小于T->Left(节点9)，在节点9和11之间执行一次单左旋转，旋转后新的根为节点9。由于查找的X小于T->Left，所以以节点9为首的右子树(称为T')中所有节点都大于X。将T‘劈开并挂到RTMin->Left上，并更新RTMin指向新的T'（节点9）。移动T，T=T->Left，新的根为节点1，并继续在新的子树上寻找。

过程2：

X大于根节点1，同时还大于T->Right(节点3)，在节点1和3之间执行一次单右旋转，旋转后新的根节点为3。此时X的值扔大于3，需要在右子树上寻找，所以以3为首的左子树(称为T')上所有的节点都小于3。将T’劈开与母树分离，挂在LTMax->Right上，并更新LTMax指向新的T'(即节点3)。移动T=T->Right，继续在右子树上寻找。

过程3：

X小于根节点7，但是X=T->Left，不需要旋转，直接将以7为首的右子树(称为T‘)与母树分离，挂在RTMin->Left上，并更新RTMin指向新的T’。最后更新T=T->Left继续寻找

过程4：

X等于根节点5，表示已找到X，退出循环并将3个子树合并。此时，H节点的左子树即RTMin上是所有大于X的节点，并且RTMin是最小的那个，T->Right(节点6)，T<T->Right<RTMin,所以将RTMin->Left = T->Right。H节点的右子树即LTMax上所有节点都小于X并且LTMax是最大的那个，因此LTMax<T->Left < X, 所以LTMax->Right = T->Left。最后需要将X替换成H节点，并翻转左右子树RTMin和LTMax。

自顶向下的伸展树实现：

static SplayTree Splay(ElementType X, Position T)
{
	static struct SplayNode Header;
	Position LeftTreeMax, RightTreeMin;

	Header.Left = Header.Right = NullNode;
	LeftTreeMax = RightTreeMin = &Header;
	NullNode->Element = X;

	while (X != T->Element) {
		if (X < T->Element) {
			if (X < T->Left->Element)//LL类型
				T = SingleRotateWithLeft(T);
			if (T->Left == NullNode)//未找到X，退出
				break;

			/* Link Right */
			RightTreeMin->Left = T;//将右子树分离
			RightTreeMin = T;
			T = T->Left;//继续在左子树查找
		} else {
			if (X > T->Right->Element)//RR类型
				T = SingleRotateWithRight(T);
			if (T->Right == NullNode)//未找到X，退出
				break;
			/* Link Left */
			LeftTreeMax->Right = T;//将左子树分离
			LeftTreeMax = T;
			T = T->Right;//继续在右子树上寻找
		}

	}

	/* 分离中树上的左右子树到LTMax和RTMin上 */
	LeftTreeMax->Right = T->Left;
	RightTreeMin->Left = T->Right;
	/* 查找到的X或者未找到的中树上的根替换成最终合成树的根节点 */
	T->Left = Header.Right;
	T->Right = Header.Left;

	return T;
}

伸展树的插入操作

SplayTree Insert(ElementType X, SplayTree T)
{
	static Position NewNode = NULL;
	if (NewNode == NULL) {
		NewNode = malloc(sizeof(struct SplayNode));
		if (NULL == NewNode) {
			printf("Out of memory\n");
			return T;
		}
	}

	NewNode->Element = X;

	if (T == NULL) {
		NewNode->Right = NewNode->Left = NullNode;
		T = NewNode;
	} else {
		T = Splay(X, T);//按照X大小伸展T，伸展后插入到左子树或右子树中
		if (X < T->Element) {//插入到左子树中
			NewNode->Left = T->Left;
			NewNode->Right = T;
			T->Left = NullNode;
			T = NewNode;
		} else if (X > T->Element) {//插入到右子树中
			NewNode->Right = T->Right;
			NewNode->Left = T;
			T->Right = NullNode;
			T = NewNode;
		} else
			return T;	//新节点已经在伸展树中
	}

	NewNode = NULL;//用于下次继续分配新插入的节点
	return T;
}

伸展树的删除操作

SplayTree Insert(ElementType X, SplayTree T)
{
	static Position NewNode = NULL;
	if (NewNode == NULL) {
		NewNode = malloc(sizeof(struct SplayNode));
		if (NULL == NewNode) {
			printf("Out of memory\n");
			return T;
		}
	}

	NewNode->Element = X;

	if (T == NULL) {
		NewNode->Right = NewNode->Left = NullNode;
		T = NewNode;
	} else {
		T = Splay(X, T);//按照X大小伸展T，伸展后插入到左子树或右子树中
		if (X < T->Element) {//插入到左子树中
			NewNode->Left = T->Left;
			NewNode->Right = T;
			T->Left = NullNode;
			T = NewNode;
		} else if (X > T->Element) {//插入到右子树中
			NewNode->Right = T->Right;
			NewNode->Left = T;
			T->Right = NullNode;
			T = NewNode;
		} else
			return T;	//新节点已经在伸展树中
	}

	NewNode = NULL;//用于下次继续分配新插入的节点
	return T;
}

解释下删除操作，想删除值为X的节点，先将树进行伸展，如果能找到值问X的节点T，那么T处于根节点的位置。T的左右子树都不为空时，将T->Left子树按照X进行伸展。也就是说在所有节点都小于X的节点的子树上伸展X，其伸展后的结果是根节点的右子树肯定为空。例如在下图进行伸展3

            1

    0            2

伸展后的结果为：

                 2

           1

      0