目录
傅里叶变换方法认为任意一个具有连续周期的信号可以根据一组由正弦和余弦曲线构成的三角函数的曲线组合而成或任意逼近。经过长期以来的发展，傅里叶变换在物理学、信号处理、统计学、声学和结构力学等研究领域有着广泛的应用。
1. 傅里叶变换定义
傅里叶变换是一种全局性的分析方法，它的核心是将时间序列信号从时间域变换到频率域，实现提取波形信号的频率信息的目的，并得到信号的不同频率成分和分布情况。给定一个时序信号s(t)，它的傅里叶变换公式如下：
图 信号傅里叶时频域转换
傅里叶变换是一种全局性的信号分析方法，因此，对于类似地震信号的非线性、非平稳的信号，傅里叶变换具有一定的局限性。傅里叶变换并不能很好的表示信号的局部时频信息，同时只能得到信号的频率和振幅之间的关系，只能获得整个信号总体上所包含的频率成分和简单的信号时变特征频谱，对于信号在不同时间上的频率分布并不能很好的表达出来。
2. 频率轴设置
在傅里叶变换的matlab仿真中，频率轴对应的范围并不是（0，fs），根据奈奎斯特采样定理可得出采样后的信号只在(0，fs/2)范围内的频率分量才有意义，实际上并不存在大于fs/2的频率分量。由于快速傅里叶变换的共轭对称性，大于fs/2的频率分量实际上是负频率的分量。因此对于fft(x)的频谱对应的频率实际上是前半部分是正频率频谱，即（0，fs/2）；后半部分频谱对应的是负频率频谱，即（-fs/2，0）。由频谱的对称性可见，频谱的一半即可表现信号的全部特征。对于单双边谱的频率轴选择代码可详见第3小节中的“图 傅里叶变换matlab仿真关键部分代码”。
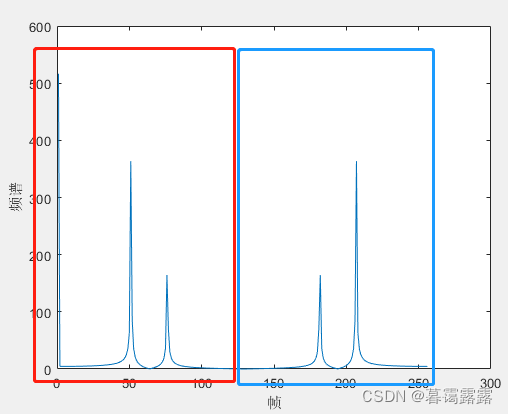
图 fft(x)频谱（未设置频率轴）
总之，频率轴范围应该是(-fs/2，fs/2)，可通过fftshift进行频谱平移转换。也可以fft只截取（0,fs/2）频率部分与频谱的前半部分，单边谱也可以完全反映信号特性。
图 fftshift(fft(x))频谱 （未设置频率轴）
3. 频谱幅度
当信号的频谱在该信号频率处取得峰值，并峰值幅度正好等于信号的幅度时，该频谱可以较好的反映信号特征。
但通常情况下，经过fft(x)变换的信号频谱与信号实际幅度并不一致。其转化方式为：
信号幅度=频谱幅度/采样点总数
在频谱的计算过程中，频谱幅度的计算需要将fft频谱值除以采样点数量。
单边谱除以N/2得到该频率的幅度，也是该频率的真实幅度；
双边谱除以N得到该频率的幅度，是信号该频率的真实幅度的一半。
图 傅里叶变换matlab仿真关键部分代码
图 频谱单边谱与双边谱的幅度差异
4. 频谱混叠
经过fft变换的信号频谱的峰值点应处于该信号频率及负信号频率，但有时由于采样率不满足奈奎斯特采样定律，将不满足上述规律。
经总结，当信号采样率不满足奈奎斯特采样定律时，此时频谱频率对应于
fa=floor(fs/f0)*fs-f0
其中，floor(fs/f0)为fs/f0的向下取整(也就是向小取整)。
同时由于频谱正负频率关于fs/2对称，因此，在未进行fftshift之前的另一根频谱的位置为
fb=f0
这也就解释了为什么当未进行fftshift时也总有正确的频率fb。但实际上fa才是真正的信号频率，fb时其未进行shift的负频率，其大小本身是无实际意义的，只是恰好等于正确的信号频率。
图 中心频率为50，采样频率为80的fft频谱
上图为信号中心频率为50Hz的信号，由于采样频率为80Hz，不满足奈奎斯特采样定理，因此
fa=fs-f0=30Hz，fb=f0=50Hz。但实际上，30Hz是频谱混叠后计算得到的频率，该图经过fftshift后，结果如下。
图 中心频率为50，采样频率为80的fftshift频谱
5. 频谱泄露
理想的频谱在信号频率处应是一个冲激信号的尖峰信号，但频谱有时却在中心频率附近的频率均有值，形成了一段频谱，同时在尖峰处的频谱幅度也降低了。
图 频谱泄露的信号图
针对此问题，主要有两个原因：
（1）信号采样不是整数周期，造成频谱泄露。
在该代码中，采样时间为t0=N/fs，信号周期为T0=1/f0，则采样周期为t0/T0不是整数周期，因此会存在频谱泄露。
（2）信号构造不按照采样频率构造
对于上述信号的构造，t的采样间隔为1/N=1/256，并不采样周期1/200的时间间隔，函数构造的不同步也会造成频谱的泄露。
6. 频谱相位
matlab计算频谱的相位使用angle函数。
图 计算信号相位代码
在计算频谱相位时，需要注意对于较小频谱的归零处理，避免干扰，如上述框红代码所示。下图为使用与不使用该行代码的相位计算结果。
图 是否归零操作的使用结果对比
5万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
