STARKs and STARK VM: Proofs of Computational Integrity

1. 引言

所谓Proofs of Computational Integrity，是指：

2. 现有ZKP证明系统

现有的ZKP证明系统主要有：

• 1）具有Succinct Verifier的ZKP系统有：
  • 1.1）Groth16：2016年
  • 1.2）STARK：2018年
  • 1.3）PLONK：2019年
  • 1.4）Marlin：2019年
  • 1.5）Sonic：2019年
  • 1.6）SuperSonic：2019年
  • 1.7）Spartan：2019年
  • 1.8）Fractal：2019年
• 2）Transparent无需可信设置的ZKP系统有：
  • 2.1）Bulletproofs：2017年
  • 2.2）Ligero：2017年
  • 2.3）STARK：2018年
  • 2.4）Aurora：2018年
  • 2.5）Spartan：2019年
  • 2.6）SuperSonic：2019年
  • 2.7）Fractal：2019年
  • 2.8）Halo：2019年
  • 2.9）Pickles：2020年
• 3）Post-Quantum抗量子ZKP系统有：
  • 3.1）Ligero：2017年
  • 3.2）Aurora：2018年
  • 3.3）STARK：2018年
  • 3.4）Fractal：2019年

这些ZKP系统从是否需要可信设置、Proof size、Prover speed、Verifier speed、密码学安全假设 维度对比如下：

根据https://github.com/matter-labs/awesome-zero-knowledge-proofs有：

	SNARKs	STARKs	Bulletproofs
Algorithmic complexity: prover	O(N * log(N))	O(N * poly-log(N))	O(N * log(N))
Algorithmic complexity: verifier	~O(1)	O(poly-log(N))	O(N)
Communication complexity (proof size)	~O(1)	O(poly-log(N))	O(log(N))
- size estimate for 1 TX	Tx: 200 bytes, Key: 50 MB	45 kB	1.5 kb
- size estimate for 10.000 TX	Tx: 200 bytes, Key: 500 GB	135 kb	2.5 kb
Ethereum/EVM verification gas cost	~600k (Groth16)	~2.5M (estimate, no impl.)	N/A
Trusted setup required?	YES 😒	NO 😄	NO 😄
Post-quantum secure	NO 😒	YES 😄	NO 😒
Crypto assumptions	DLP + secure bilinear pairing 😒	Collision resistant hashes 😄	Discrete log 😏

3. SNARKs VS STARKs

STARKs全称为：Scalable Transparent Arguments of Knowledge
SNARKs全称为：Succinct Non-interactive Arguments of Knowledge

STARKs与SNARKs的交叉区域有：

• Non-interactive STARKs
• Scalable Transparent SNARKs

3.1 SNARKs算术化表示 VS STARKs算术化表示

• 1）大多数SNARKs将程序表达为电路计算，以R1CS（Rank 1 Constraint Satisfiability）来表示，即：
  

• 2）STARKs将程序表达为machine computation，以AIR（Algebraic Intermediate Representation）来表示。
  

SNARKs的R1CS算术化表示 与 STARKs的AIR算术化表示 对比情况为：

算术化友好的计算有：

• Native CPU arithmetic：如$c=a\ast b\mathrm{mod}{2}^{64}$
• Native ZKP arithmetic：如$c=a\ast b\mathrm{mod}p$，其中$p$为某素数

除此之外，ZKP系统中还包含一些昂贵的运算：

• Non-native arithmetic：如需要对输入、输出的范围进行校验。
• 比较运算，如大于、小于：需要二进制分解。
• 位运算：如AND、OR、XOR、位移等。

ZKP系统的主要挑战在于：

• 1）证明开销：证明生成过程是昂贵的：
  • 对于算术化友好的计算，相比于直接计算，为其生成证明需增加100倍的开销；
  • 对于算术化困难的计算，相比于直接计算，为其生成证明需增加1万倍的开销。
• 2）算术化表示复杂度：高效的算术化表示是困难的：
  • 除非是最简单的计算，否则手工算术化是不可行的；
  • 直观自动化的算术化实现是可能的，但不实用。

针对以上ZKP挑战的解决方案有：

• 1）针对证明生成昂贵问题的解决方案有：
  • 使用算术化友好的密码学原语
  • 引入lookup tables（PLOOKUP）
  • 证明生成并行化
  • 硬件加速
• 2）针对算术化表示复杂度高的问题，解决方案有：
  • 采用高层级编程语言和编译器（特别适于R1CS算术化表达）
  • 引入零知识虚拟机（特别适于AIR算术化表达）

4. ZKP用例——将ZKP用于证明计算完整性

证明计算完整性需满足2个要求：

• 1）扩展性：使得验证的内容小而快，主要体现在：
  • 1.1）压缩：辅助数据可作为witness，无需与Verifier共享。
    
  • 1.2）无需重新执行：对于succinct proving system，一旦证明生成，可相比于重新执行该计算，验证该证明的速度为exponentially faster。
    
• 2）隐私性：可隐藏具体的数据和计算，具体为：
  • 2.1）数据隐私：以witness来表示隐私数据，无需对外公开。
    
  • 2.2）函数（程序）隐私：witness可对某程序编码，使得该程序也为隐私的。
    

5. 深入浅出STARKs

5.1 STARKs优缺点

STARKs的优势主要有：

• 1）Transparent：无需可信设置，无需预处理；
• 2）精干的密码学：仅需要抗碰撞哈希函数，是量子安全的；
• 3）灵活性：
  • 适于多个不同的域
  • 在Prover-time 和 proof size之间权衡
  • 在security level 和 proof size之间权衡
• 4）性能：
  • 4.1）具有超轻Verifier：
    • 大多数证明验证时间为2~5ms；
    • 具有简洁的计算描述
  • 4.2）非常快的Prover：
    • 在单核CPU上，为15K zk VM cycles/sec（对于Matic Miden VM）；
    • 可大规模并行化：在64核CPU上，速度高达400K cycles/sec。

STARKs的劣势主要有：

• 1）proof size：为数十KB：
  • 约15KB for preimage of Rescue哈希函数
  • 约120KB for 1M cycles of virtual machine execution
• 2）递归有限：可实现递归STARKs，但当前未论证
• 3）算术化表示：
  • AIR算术化表示方法比R1CS更复杂；
  • 相关工具仍在开发中。

5.2 STARK证明生成

STARK证明生成流程为：

• 1）将待证明的计算 以 execution trace表示；
• 2）将execution trace的每列（寄存器）的值作为某多项式的$f(x)$的evaluations，基于trace domain $D_{trace}$插值获得$f(x)$，然后再基于更大的evaluation domain $D_{lde}$对$f(x)$进行evaluate。
• 3）定义transition constraints和boundary constraints等约束，以多项式$p(x)$来表示。
• 4）对多项式$p(x)$采用FRI协议进行证明。

5.2.1 STARK Execution trace

STARK第一步Execution trace的核心思想为：

• 1）为待证明的计算 定义state transition logic，即transition function；
• 2）运行该transition function $n$步；
• 3）记录在每步计算中，transition function的结果。

比如，在32-bit素数域内（如模为：$125\ast 2^{25}+1$，与$2^{32}-3\ast 2^{25}+1$等价），计算斐波那契数列的第64项值：

• Prover待证明内容为：
  

对应的Fibonacci execution trace表达方式有：

• 1）表达方式1：$r_{i+2}=r_{i+1}+r_i$
  相应的execution trace参数为：
  • 寄存器：1个
  • 计算步数：64步
  • 域模：$125\ast 2^{25}+1$
    
• 2）表达方式2：$r_{0,i+1}=r_{0,i}+r_{1,i}$ 以及 $r_{1,i+1}=r_{0,i}+2\ast r_{1,i}$
  相应的execution trace参数为：
  • 寄存器：2个
  • 计算步数：32步
  • 域模：$125\ast 2^{25}+1$
    

5.2.2 STARK Low Degree Extension

STARK Low Degree Extension（LDE）核心思想为：

• 1）将每个register trace解析为某多项式$f(x)$的evaluations；
• 2）基于某trace domain $D_{trace}$，对$f(x)$进行插值。
  如以execution trace的某register列（ r 0 = { y 0 , y 1 , y 2 , y 3 } r_0=\{y_0,y_1,y_2,y_3\} r0​={y0​,y1​,y2​,y3​}）为例，基于trace domain D t r a c e = { x 0 , x 1 , x 2 , x 3 } D_{trace}=\{x_0,x_1,x_2,x_3\} Dtrace​={x0​,x1​,x2​,x3​} 插值获得的$f(x)$多项式为：【多项式$f(x)$的degree为$|D_{trace}|-1$】
  
• 3）基于某更大的evaluation domain $D_{lde}$，对$f(x)$进行evaluate。
  基于更大的evaluation domain D l d e = { x 0 ′ , x 1 ′ , x 2 ′ , x 3 ′ , x 4 ′ , x 5 ′ , x 6 ′ , x 7 ′ } D_{lde}=\{x_0',x_1',x_2',x_3',x_4',x_5',x_6',x_7'\} Dlde​={x0′​,x1′​,x2′​,x3′​,x4′​,x5′​,x6′​,x7′​}，对步骤2）中获得的多项式$f(x)$进行evaluate，有：
  

以上有2个domain：

• 1）trace domain $D_{trace}$
• 2）evaluation domain $D_{lde}$

若将trace domain $D_{trace}$ 4倍放大为 evaluation domain $D_{lde}$，二者的关系为：

其中，${\omega }_{trace}$为某multiplicative sub-group of size $n$的generator，且${\omega }_{lde}^4={\omega }_{trace}$。

仍以上面的斐波那契数列为例，其域模为：$125\ast 2^{25}+1$。
对于只有单个寄存器的execution trace表示，其包含了64步，取size为$64$的multiplicative sub-group为$D_{trace}$，相应的generator为${\omega }_{64}$。
将$D_{trace}$放大4倍为$D_{lde}$，$D_{lde}$对应size为$64\times 4=512$的multiplicative sub-group，其generator为${\omega }_{512}$。

STARK execution trace经Low Degree Extension之后，获得了Extended execution trace。

5.2.3 STARK Constraint Evaluation

STARK Constraints核心思想为：

• 1）定义execution trace寄存器之间的代数关系；
• 2）将这些代数关系重新解析为多项式，在该多项式的root points位置，其值对应为该关系成立的位置（Reinterpet these relationships as polynomials with roots at points where relationships hold）；
• 3）从constraint polynomials中除以相应的roots，将其转换为rational constraints。

STARK中主要包含2种约束类型：

• 1）Transition Constraints：描述了计算的2步或多步之间的代数关系。
• 2）Boundary Constraints：断言了计算中特定步数的特定寄存器的值。（Assert values of specific registers at specific steps in the computation.）

仍然以斐波那契数列的单个寄存器execution trace表示为例，其Transition Constraints为：
$r_{i+2}=r_{i+1}+r_i$，for $0\le i\le 61$

在Low Degree Extension（LDE）步骤中，对trace domain D t r a c e = { ω 0 , ω 2 , ω 3 , ⋯   , ω 63 } D_{trace}=\{\omega^0,\omega^2,\omega^3,\cdots,\omega^{63}\} Dtrace​={ω0,ω2,ω3,⋯,ω63} 插值获得了多项式$f(x)$，基于多项式$f(x)$的Transition Constraints表示为：
$f(x\ast {\omega }^2)=f(x\ast \omega )+f(x)$，for $x={\omega }^i$ where $0\le i\le 61$。
进一步将其表示为多项式$p(x)$：
$p(x)=f(x\ast {\omega }^2)-f(x\ast \omega )-f(x)$
其中多项式$p(x)$的roots为：${\omega }^i$ where $0\le i\le 61$。

多项式可除性（Polynomial divisibility）是指：
$$\frac{p(x)}{x-z}$$
多项式的degree为$d$，当且仅当：

• 1）$p(x)$多项式degree为$d+1$；
• 2）$z$为$p(x)$的根。

定义diviosr polynomial：
$$z(x)=(x-{\omega }^0)\cdot (x-{\omega }^1)\cdots (x-{\omega }^{61})$$
为product of all divisors of $p(x)$。
有：

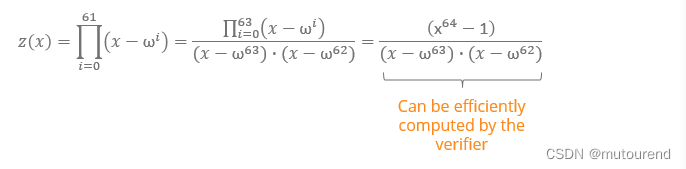
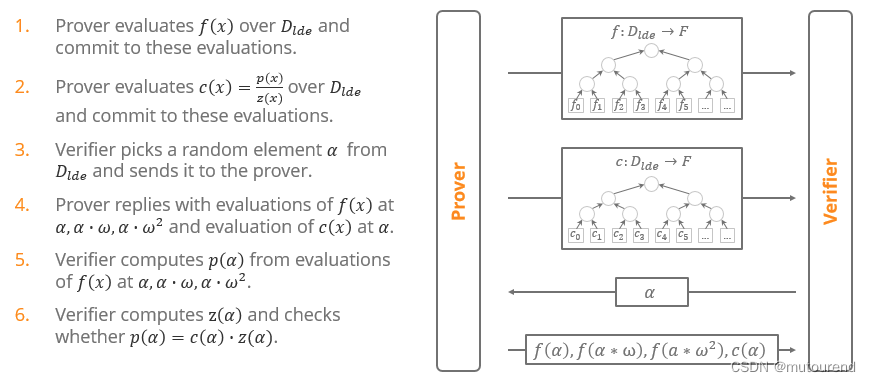
Prover与Verifier的交互流程为：

• 1）Prover：基于$D_{lde}$域，对$f(x)$进行evaluate，并对所有evaluations进行commit。
• 2）Prover：基于$D_{lde}$域，对$c(x)=\frac{p(x)}{z(x)}$进行evaluate，并对所有evaluations进行commit。
• 3）Verifier：从$D_{lde}$中选择随机值$\alpha$发送给Prover。
• 4）Prover：回复$f(x)$在$\alpha ,\alpha \cdot \omega ,\alpha \cdot {\omega }^2$处的evaluations，以及$c(x)$在$\alpha$处的evaluation值。
• 5）Verifier：根据$p(\alpha )=f(\alpha \cdot {\omega }^2)-f(\alpha \cdot \omega )-f(\alpha )$计算$p(\alpha )$值。
• 6）Verifier：可根据$z(x)$公式高效计算出$z(\alpha )$值，并检查$p(\alpha )=c(\alpha )\cdot z(\alpha )$是否成立。
  

以上对于transition constraints证明过程的soundness分析为：
Fact：2个不同的degree为$d$的多项式，最多有$d$个点是相等的。
$\mathrm{deg}(p(x))=\mathrm{deg}(c(x)\ast z(x))=|D_{trace}|-1$
从而，若$p(x)$和$c(x)\ast z(x)$不是相同的多项式，Verifier误判的概率为$\epsilon =\frac{|D_{trace}|-1}{|D_{lde}|}$。
若将$D_{trace}$放大16倍为$D_{lde}$，则，误判概率为：
$\epsilon =\frac{63}{64\ast 16}\approx 6\%$

transition constraints证明过程中，若query 24次不同的点，则可达到100-bit security level。

以上考虑完斐波那契数列例子中的Transition constraints之外，接下来讲考虑边界约束Boundary constraints了：

• Step 0，对于root ${\omega }^0$，有$f(x)=1$，构建多项式$p_1(x)=f(x)-1$；
• Step 1，对于root ${\omega }^1$，有$f(x)=1$，构建多项式$p_2(x)=f(x)-1$；
• 最后一步，Step 63，对于root ${\omega }^{63}$，有$f(x)=2815039194$，构建多项式$p_3(x)=f(x)-2815039194$。

其它约束表达有：

• 1）如约束某列$r_0$中所有值均必须为二进制的，即0或1，相应的约束表达为：
  $$\frac{(f_0(x)-1)\ast f_0(x)}{(x^n-1)}$$
• 2）如约束除最后一步之外，所有步数满足$r_{0,i+1}=r_{0,i}\ast r_{1,i}$（当$r_0,r_1$均为二进制时，等价为AND gate操作，）相应的约束表达为：
  $$\frac{f_0(x\ast w)-f_0(x)\ast f_1(x)}{(x^n-1)/(x-{\omega }^{n-1})}$$
• 3）如约束除最后一步之外，所有步数均满足：
  $$r_{0,i+1}=\{\begin{array}{cc}{r}_{0,i}& \text{当 }{r}_{2,i}=1\\ r_{1,i}& \text{当 }{r}_{2,i}=0\end{array}$$
  相应的约束表达为：
  $$\frac{f_0(x\ast \omega )-f_2(x)\ast f_0(x)-(1-f_2(x))\ast f_1(x)}{(x^n-1)/(x-{\omega }^{n-1})}$$

5.2.4 FRI protocol

所谓Degree-respecting projection（DRP）是指：


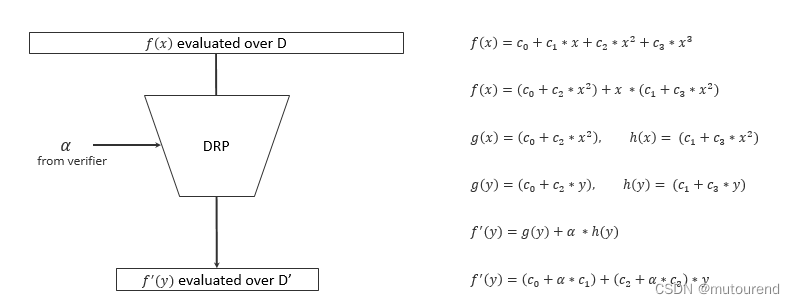
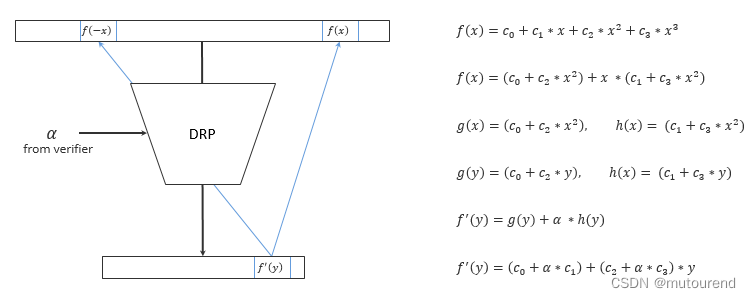
FRI testing polynomiality，是指针对：

• 函数：$f(x)=c_0+c_1\cdot x+c_2\cdot x^2+\cdots +c_k\cdot x^{k-1}$
• domain：$D=1,\omega ,{\omega }^2,\cdots ,{\omega }^{8\ast k-1}$
• evaluations：$f:D\to F=e_0,e_1,e_2,\cdots ,e_{8\ast k1}$

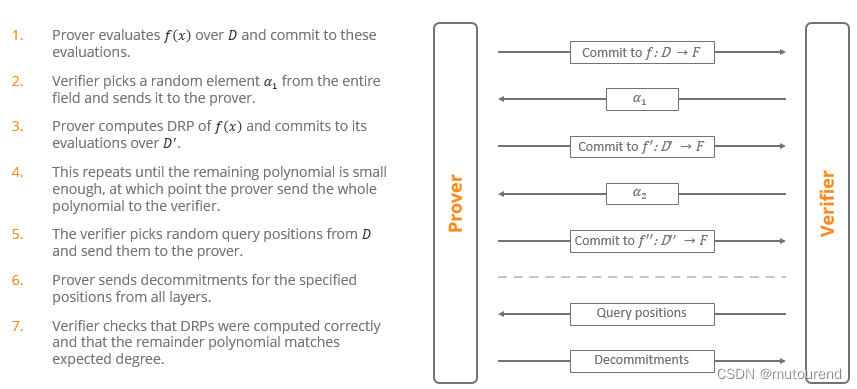
Prover在仅发送$O(\log k)$个evaluation值的情况下，向Verifier证明$f:D\to F$为evaluations of polynomial of degree less than $k$ 的证明流程为：

• 1）Prover：evaluate $f(x)$ over $D$，并对这些evaluations进行commit。
• 2）Verifier：从整个域中选择随机值${\alpha }_1$发送给Prover。
• 3）Prover：计算$f(x)$的DRP，并对其evaluations over $D^{\prime }$进行commit。
• 4）重复以上过程，直到剩余的多项式足够小，此时Porver会将剩余的整个多项式发送给Verifier。
• 5）Verifier：从$D$中选择随机query位置发送给Prover。
• 6）Prover：将所有层的特定位置的decommitments发送给Verifier。
• 7）Verifier：检查所有层的DRP计算正确，并检查remainder polynomial与期待的degree匹配。
  

6. 基于STARK的虚拟机——STARK VM

虚拟机定义为：

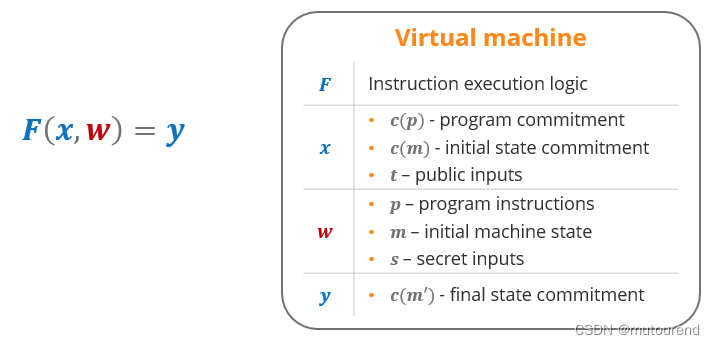
VM在设计时需考虑以下维度：

• 1）machine类型：
  • 1.1）Stack machine
  • 1.2）Register machine
  • 1.3）Memory-memory machine
• 2）Flow control：
  • 2.1）哈佛架构
  • 2.2）冯·诺依曼架构
  • 2.3）Merkelized abstract syntax tree（MAST）
• 3）Program input：
  • 3.1）Program hash
  • 3.2）Public memory
  • 3.3）Codeword commitment
• 4）Function calls：
  • 4.1）Static call targets VS dynamic call targets
• 5）Memory model：
  • 5.1）Write-once memory VS read-write memory
  • 5.2）Addressing model
• 6）Native data types：
  • 6.1）Field elements
  • 6.2）Regular integers（如u32）
  • 6.3）Structs、arrays、sets等
• 7）Native field：
  • 7.1）64-bit VS 128-bit VS 256-bit

一个玩具虚拟机为例：

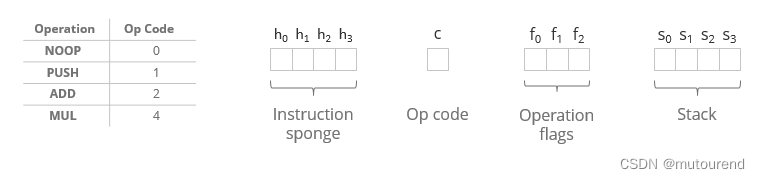
相应的程序运行示例为：

相应的约束有：

• 1）Op flags必须为binary，即：$f_i^2-f_i=0$
• 2）Op flags必须与Op code一致，即：$c-(f_0+2\ast f_1+4\ast f_2)=0$
• 3）一次仅能设置一个Op flag，即：$1-(f_0+f_1+f_2)-(1-f_0)\ast (1-f_1)\ast (1-f_2)=0$
• 4）需基于Op flags来更新stack，
  
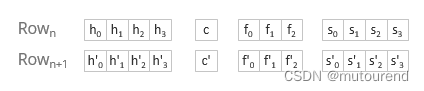
  即：
  

7. 附录

7.1 STARK fields

• 1）STARK通常使用素数域，但也可使用binary fields。
• 2）STARK的安全性不依赖于底层域的size。如64-bit和128-bit fields都可提供over 100 bits of security，但是对于很小的域会有一些注意事项。
• 3）STARK友好的素数域，通常具有a large multiplicative sub-group with order $2^n$。任意素数域的模形如$k\ast 2^n+1$（Proth primes），其中$n$大于32即满足该条件。

7.2 STARK security level

STARK proof 的security依赖于：

• Size of the prime field $q$
• Length of the exectuion trace $t$
• Maximum degree of constraints $d$
• Domain blowup factor $b$
• Collision resistance of the hash function $c$
• Nummber of queries $n$

其security为：
$$\min ({\log }_2(\frac{q}{t\ast b}),{\log }_2(\frac{b}{d})\ast n,c)$$

如某STARK proof参数为：

• Size of the prime field $q=2^{128}$
• Length of the exectuion trace $t=2^{20}$
• Maximum degree of constraints $d=4$
• Domain blowup factor $b=32$
• Collision resistance of the hash function $c=128$
• Nummber of queries $n=38$

相应的security为：
$$\min ({\log }_2(\frac{2^{128}}{2^{25}}),{\log }_2(\frac{32}{4})\ast 38,128)=\min (113,114,128)=113$$

7.3 STARK prover complexity

STARK proof生成时间依赖于：

• Size of the prime field $q$
• Length of the exectuion trace $t$
• Width of the execution trace $w$
• Maximum degree of constraints $d$

相应的prover complexity为：
$$(\frac{{\log }_{2}q}{64}{)}^2\ast (d+2)\ast t\ast {\log }_{2}t$$

参考资料

[1] Proofs of Computational Integrity