本节目标:
通过对点阵的连通分析,看是否能达到有效分割多边形的目标。
实现步骤:
我这次主要是想看看一个多边形要怎样才能被不重不漏的分成若干个三角形,
但这个目标不知道能不能实现。
为了测试,先写了以下代码:
//解决某个特定问题
function problemSolve(pointArray) {
//传入点阵列pointArray
//格式为[[px1, py1], [px2, py2], ...]
//document.write(pointArray.join(' , ')+'<br/>');
//对于pointArray中的每个点,求它与所有其它点的距离
//结果放入distanceArray
//格式为[[点1序号,点2序号, 距离值]]
var distanceArray = [];
//点的数量
var size = pointArray.length;
//临时变量
var distance = x1 = y1 = x2 = y2 = 0;
//计算并压入距离
for (var i = 0; i < size; i++) {
for (var j = i+1; j < size; j++) {
x1 = pointArray[i][0];
y1 = pointArray[i][1];
x2 = pointArray[j][0];
y2 = pointArray[j][1];
distance = Math.sqrt(Math.pow(x1-x2, 2)+Math.pow(y1-y2, 2));
//注意这里已经保证i < j
//所以起始点序号必须要小于终点序号
//这是为了连接起始点和终点的直线不会重复
distanceArray.push([i, j, distance]);
}
}
//对距离阵列排序
//排序权重:起始点序号 > 距离 > 终点序号
distanceArray.sort(function(a, b) {
if (a[0] == b[0]) {
if (Math.abs(a[2] - b[2]) < 0.000001) {
return a[1]-b[1];
}
else {
return a[2]-b[2];
}
}
else {
return a[0] - b[0];
}
});
//document.write(distanceArray.join(' , ')+'<br/>');
return distanceArray;
}
//去除重复点
function removeDuplicatedPoint(pointArray) {
var array = new Array();
var size = pointArray.length;
array.push(pointArray[0]);
var len = 0;
for (var i = 0; i < size; i++) {
len = array.length;
for (var j = 0; j < len; j++) {
if (pointArray[i][0] == array[j][0] &&
pointArray[i][1] == array[j][1]) {
break;
}
if (j >= len-1) {
array.push(pointArray[i]);
}
}
}
return array;
}然后这里是测试用例:
<span style="font-size:18px;"> var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0, 180);
//点的坐标阵列
//格式为[[px1, py1], [px2, py2], ...]
var array = [
[0,2], [3, 3], [4,5], [4, 6], [4, 5], [-1,-2],[-3,-4],
[-6,-8], [-9, -10], [12,-2], [15,-8], [-6,7], [-7,12]
];
//去除重复点
var pointArray = removeDuplicatedPoint(array);
//无重复的点的数量
var points = pointArray.length;
//得到距离阵列
//格式为[[点1序号,点2序号, 距离值], ...]
var distanceArray = problemSolve(pointArray);
//边的数量
var edges = distanceArray.length;
//存放需要连通的边
var linkedArray = [];
//连通的边的数量
var links = 0;
//每个顶点相关的边的集合
var edgeOfVertex = [];
for (var i = 0; i < points; i++) {
//获得顶点相关的边的集合
edgeOfVertex = [];
for (var j = 0; j < edges; j++) {
if (distanceArray[j][0] == i ||
distanceArray[j][1] == i) {
edgeOfVertex.push(distanceArray[j]);
}
}
//根据起始点寻找最短长度的两条边
edgeOfVertex.sort(function(a, b) {
return a[2] - b[2];
});
var choice = 1;
if (edgeOfVertex.length > choice) {
edgeOfVertex = edgeOfVertex.slice(0, choice);
}
linkedArray = linkedArray.concat(edgeOfVertex);
}
//document.write(linkedArray.join(' , ')+'<br/>');
linkedArray = removeDuplicatedPoint(linkedArray);
links = linkedArray.length;
//document.write(linkedArray.join(' , ')+'<br/>');
var startPoint, endPoint, x1, y1, x2, y2;
//比例缩放
var scale = 15;
for (var i = 0; i < links; i++) {
startPoint = linkedArray[i][0];
endPoint = linkedArray[i][1];
x1 = pointArray[startPoint][0];
y1 = pointArray[startPoint][1];
x2 = pointArray[endPoint][0];
y2 = pointArray[endPoint][1];
shape.multiLineDraw([[x1,y1], [x2, y2]], 'red', scale);
}
shape.pointDraw(pointArray, 'blue', scale);</span>见证效果的时刻:
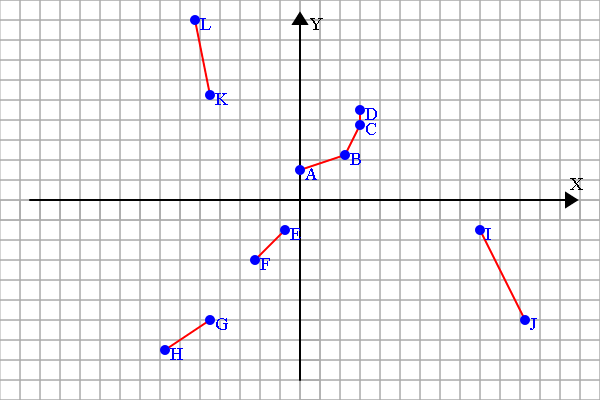
有一个叫做choice的参数,它的意义是可以选择最短距离序列中的前几个,比如只选最短的:
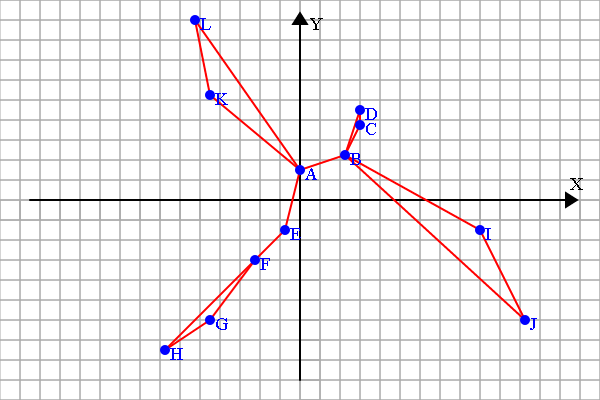
如果每个点可以有两个选择呢?
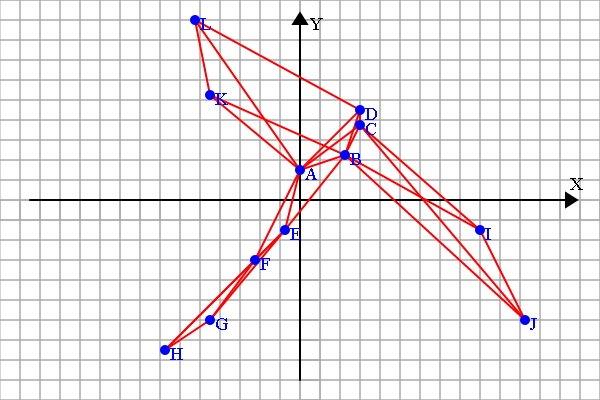
如果可以有三个选择呢?
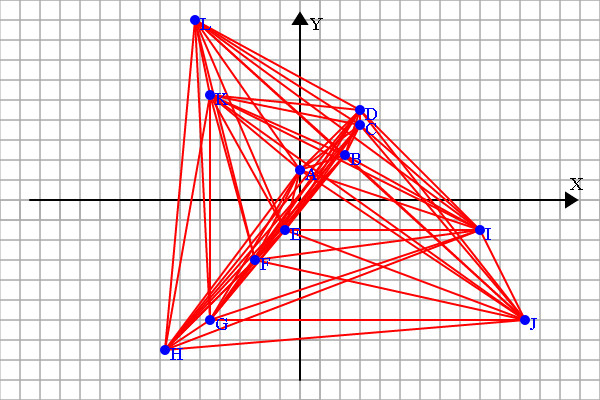
如果这个选择其实很多,比如100,会怎样呢?
到现在为止,其实我还没想明白到底发生了什么,不过,好像要另换一组点来试验一下比较好。
<span style="font-size:18px;"> //点的坐标阵列
//格式为[[px1, py1], [px2, py2], ...]
var array = [
[-2, -2], [2, -2], [2, 2], [-2, 2]
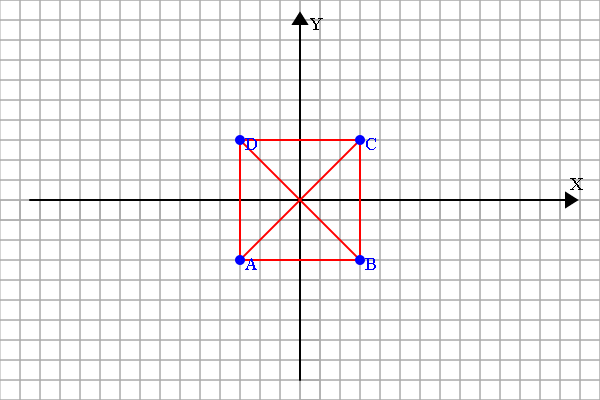
];</span>这是一个正方形的顶点,看看会发生什么。
选择太多,重复了。
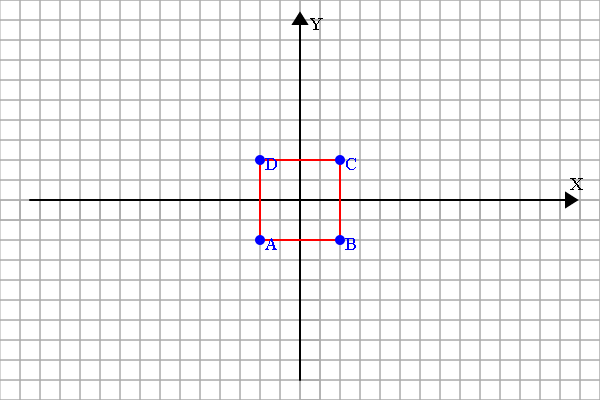
选择为2的情况,没有分割开:
其实我是想只要一条对角线的,但好像做不到。
先到这里吧,有些问题我还要好好想想。
本节到此结束。








 本节关注Canvas中通过连通分析来尝试将多边形分割成三角形的问题。作者通过编写代码进行测试,探讨了不同选择数量(如最短距离序列的前几个)对分割效果的影响,并发现选择过多可能导致重复或无法实现预期的单一对角线分割。目前,作者尚未完全理解现象并计划进一步试验。
本节关注Canvas中通过连通分析来尝试将多边形分割成三角形的问题。作者通过编写代码进行测试,探讨了不同选择数量(如最短距离序列的前几个)对分割效果的影响,并发现选择过多可能导致重复或无法实现预期的单一对角线分割。目前,作者尚未完全理解现象并计划进一步试验。














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








