一、组合逻辑电路概述
数字逻辑电路
- 组合逻辑电路
- 时序逻辑电路
组合电路特点
- 功能上:输出仅与该时刻的输入有关
- 结构上:由门电路组成
主要内容
- 组合电路的分析、设计方法(对小规模集成电路)
- 常用集成组合逻辑电路(对中规模集成电路)
组合逻辑电路:输出跟随输入的变化
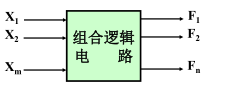
- 输入: X 1 , X 2 , … , X m X_1 , X_2 ,… , X_m X1,X2,…,Xm
- 输出: F 1 , F 2 , … , F n F_1 , F_2 , … , F_n F1,F2,…,Fn
逻辑关系:
F 1 = f 1 ( X 1 , X 2 , . . . , X m ) F 2 = f 2 ( X 1 , X 2 , . . . , X m ) F n = f n ( X 1 , X 2 , . . . , X m ) \begin{aligned} F_1 &= f_1(X_1,X_2,...,X_m)\\ F_2 &= f_2(X_1,X_2,...,X_m)\\ F_n &= f_n(X_1,X_2,...,X_m)\\ \end{aligned} F1F2Fn=f1(X1,X2,...,Xm)=f2(X1,X2,...,Xm)=fn(X1,X2,...,Xm)
组合电路的特点: :
- 电路中不包含记忆元件
- 输出无反馈到输入的回路
- 任意时刻 , 电路的输出仅取决于当时的输入
二、组合逻辑电路分析
分析目的
- 找出输出函数与输入变量的逻辑关系,确定电路所实现的逻辑功能
分析方法 - 从输入级开始,逐级写出门的逻辑表达式
- 对表达式进行化简
- 列真值表
- 描述电路的逻辑功能
组合逻辑电路的级数:输入信号从输入端到输出端所经历的逻辑门的最大数目

例1:试分析下图所示逻辑电路的功能。

解 : 该电路为二级组合电路。
(1) 写出电路的逻辑表达式
F = A + B ‾ + A B ‾ = ( A + B ) ( A ‾ + B ‾ ) = A ‾ B + A B ‾ \begin{aligned} F &= \overline {\overline {A+B} + AB}\\ &= (A+B)(\overline A + \overline B)\\ &= \overline AB + A\overline B \end{aligned} F=A+B+AB=(A+B)(A+B)=AB+AB
(2) 描述电路的逻辑功能:该函数表达式比较简单,不用列真值表,由表达式可知此电路是一个异或电路 。
例2 :试分析图中所示逻辑电路的功能。

(1) 写出电路的逻辑表达式
F = F 1 ⋅ F 2 ⋅ F 3 ‾ = A B ‾ ⋅ B C ‾ ⋅ A C ‾ ‾ = A B + B C ‾ + A C \begin{aligned} F&=\overline {F_1 \cdot F_2 \cdot F_3}\\ &=\overline {\overline {AB} \cdot \overline {BC} \cdot \overline {AC}}\\ &= AB +B\overline C+AC \end{aligned} F=F1⋅F2⋅F3=AB⋅BC⋅AC=AB+BC+AC
(2) 列真值表

(3) 描述电路的逻辑功能:
- 多数输入变量为1 ,输出 F F F 为 1 1 1
- 多数输入变量为0 ,输出 F F F 为 0 0 0
因此,该电路为少数服从多数电路,也称多数表决电路。
例3:试分析图中所示电路逻辑,写出表达式。

(1) 写出电路的逻辑表达式
G 3 = B 3 G 2 = B 3 ⊕ B 2 G 1 = B 2 ⊕ B 1 G 0 = B 1 ⊕ B 0 \begin{aligned} G_3 &= B_3\\ G_2 &= B_3 \oplus B_2\\ G_1 &= B_2 \oplus B_1\\ G_0 &= B_1 \oplus B_0 \end{aligned}








 本文深入探讨了组合逻辑电路的设计与分析,详细讲解了电路原理、功能特性及设计方法,辅以实例解析,适合电子工程专业学生及电路设计爱好者学习。
本文深入探讨了组合逻辑电路的设计与分析,详细讲解了电路原理、功能特性及设计方法,辅以实例解析,适合电子工程专业学生及电路设计爱好者学习。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 5025
5025

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










