author: Marcythm, Ir1d, Ycrpro, Xeonacid, konnyakuxzy, CJSoft, HeRaNO, ethan-enhe, ChungZH, Chrogeek, hsfzLZH1, billchenchina, orzAtalod, luoguojie, Early0v0, wy-luke
## 引入
线段树是算法竞赛中常用的用来维护 **区间信息** 的数据结构。
线段树可以在 $O(\log N)$ 的时间复杂度内实现单点修改、区间修改、区间查询(区间求和,求区间最大值,求区间最小值)等操作。
## 线段树
### 线段树的基本结构与建树
#### 过程
线段树将每个长度不为 $1$ 的区间划分成左右两个区间递归求解,把整个线段划分为一个树形结构,通过合并左右两区间信息来求得该区间的信息。这种数据结构可以方便的进行大部分的区间操作。
有个大小为 $5$ 的数组 $a=\{10,11,12,13,14\}$,要将其转化为线段树,有以下做法:设线段树的根节点编号为 $1$,用数组 $d$ 来保存我们的线段树,$d_i$ 用来保存线段树上编号为 $i$ 的节点的值(这里每个节点所维护的值就是这个节点所表示的区间总和)。
我们先给出这棵线段树的形态,如图所示:
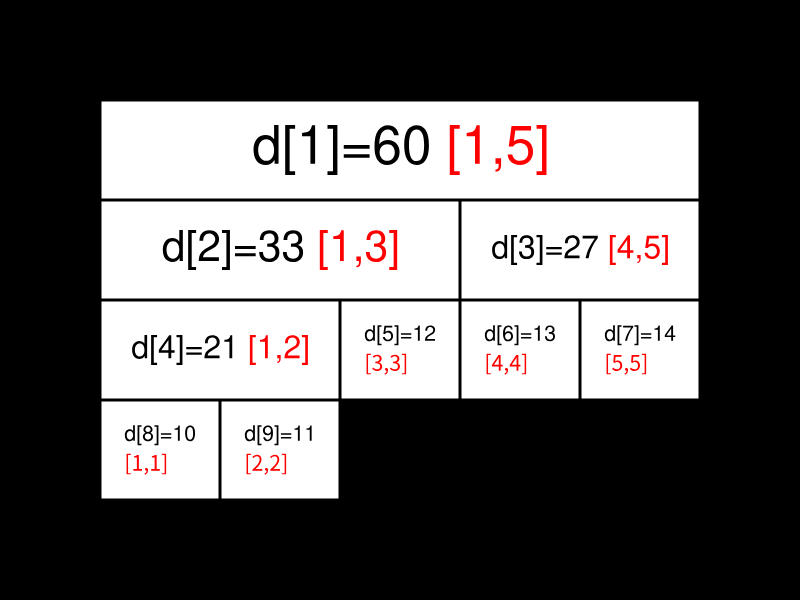
图中每个节点中用红色字体标明的区间,表示该节点管辖的 $a$ 数组上的位置区间。如 $d_1$ 所管辖的区间就是 $[1,5]$($a_1,a_2, \cdots ,a_5$),即 $d_1$ 所保存的值是 $a_1+a_2+ \cdots +a_5$,$d_1=60$ 表示的是 $a_1+a_2+ \cdots +a_5=60$。
通过观察不难发现,$d_i$ 的左儿子节点就是 $d_{2\times i}$,$d_i$ 的右儿子节点就是 $d_{2\times i+1}$。如果 $d_i$ 表示的是区间 $[s,t]$(即 $d_i=a_s+a_{s+1}+ \cdots +a_t$)的话,那么 $d_i$ 的左儿子节点表示的是区间 $[ s, \frac{s+t}{2} ]$,$d_i$ 的右儿子表示的是区间 $[ \frac{s+t}{2} +1,t ]$。
在实现时,我们考虑递归建树。设当前的根节点为 $p$,如果根节点管辖的区间长度已经是 $1$,则可以直接根据 $a$ 数组上相应位置的值初始化该节点。否则我们将该区间从中点处分割为两个子区间,分别进入左右子节点递归建树,最后合并两个子节点的信息。
#### 实现
此处给出代码实现,可参考注释理解:
```cpp
void build(int s, int t, int p) {
// 对 [s,t] 区间建立线段树,当前根的编号为 p
if (s == t) {
d[p] = a[s];
return;
}
int m = s + ((t - s) >> 1);
// 移位运算符的优先级小于加减法,所以加上括号
// 如果写成 (s + t) >> 1 可能会超出 int 范围
build(s, m, p * 2), build(m + 1, t, p * 2 + 1);
// 递归对左右区间建树
d[p] = d[p * 2] + d[(p * 2) + 1];
}
```
=== "Python"
```python
def build(s, t, p):
# 对 [s,t] 区间建立线段树,当前根的编号为 p
if s == t:
d[p] = a[s]
return
m = s + ((t - s) >> 1)
# 移位运算符的优先级小于加减法,所以加上括号
# 如果写成 (s + t) >> 1 可能会超出 int 范围
build(s, m, p * 2); build(m + 1, t, p * 2 + 1)
# 递归对左右区间建树
d[p] = d[p * 2] + d[(p * 2) + 1]
```
关于线段树的空间:如果采用堆式存储($2p$ 是 $p$ 的左儿子,$2p+1$ 是 $p$ 的右儿子),若有 $n$ 个叶子结点,则 d 数组的范围最大为 $2^{\left\lceil\log{n}\right\rceil+1}$。
分析:容易知道线段树的深度是 $\left\lceil\log{n}\right\rceil$ 的,则在堆式储存情况下叶子节点(包括无用的叶子节点)数量为 $2^{\left\lceil\log{n}\right\rceil}$ 个,又由于其为一棵完全二叉树,则其总节点个数 $2^{\left\lceil\log{n}\right\rceil+1}-1$。当然如果你懒得计算的话可以直接把数组长度设为 $4n$,因为 $\frac{2^{\left\lceil\log{n}\right\rceil+1}-1}{n}$ 的最大值在 $n=2^{x}+1(x\in N_{+})$ 时取到,此时节点数为 $2^{\left\lceil\log{n}\right\rceil+1}-1=2^{x+2}-1=4n-5$。
### 线段树的区间查询
#### 过程
区间查询,比如求区间 $[l,r]$ 的总和(即 $a_l+a_{l+1}+ \cdots +a_r$)、求区间最大值/最小值等操作。
仍然以最开始的图为例,如果要查询区间 $[1,5]$ 的和,那直接获取 $d_1$ 的值($60$)即可。
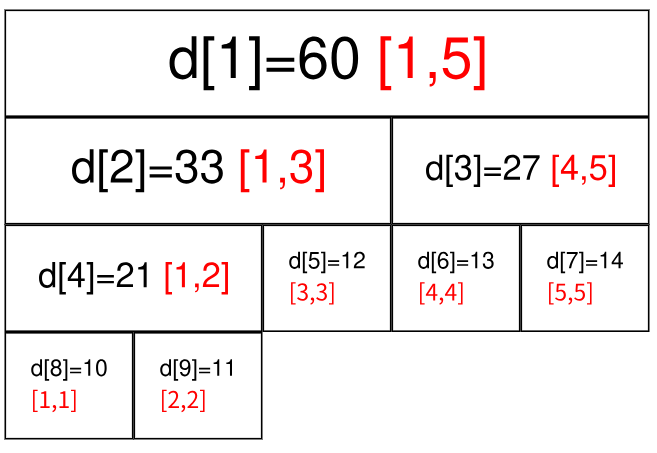
如果要查询的区间为 $[3,5]$,此时就不能直接获取区间的值,但是 $[3,5]$ 可以拆成 $[3,3]$ 和 $[4,5]$,可以通过合并这两个区间的答案来求得这个区间的答案。
一般地,如果要查询的区间是 $[l,r]$,则可以将其拆成最多为 $O(\log n)$ 个 **极大** 的区间,合并这些区间即可求出 $[l,r]$ 的答案。
#### 实现
此处给出代码实现,可参考注释理解:
```cpp
int getsum(int l, int r, int s, int t, int p) {
// [l, r] 为查询区间, [s, t] 为当前节点包含的区间, p 为当前节点的编号
if (l <= s && t <= r)
return d[p]; // 当前区间为询问区间的子集时直接返回当前区间的和
int m = s + ((t - s) >> 1), sum = 0;
if (l <= m) sum += getsum(l, r, s, m, p * 2);
// 如果左儿子代表的区间 [s, m] 与询问区间有交集, 则递归查询左儿子
if (r > m) sum += getsum(l, r, m + 1, t, p * 2 + 1);
// 如果右儿子代表的区间 [m + 1, t] 与询问区间有交集, 则递归查询右儿子
return sum;
}
```
```python
def getsum(l, r, s, t, p):
# [l, r] 为查询区间, [s, t] 为当前节点包含的区间, p 为当前节点的编号
if l <= s and t <= r:
return d[p] # 当前区间为询问区间的子集时直接返回当前区间的和
m = s + ((t - s) >> 1); sum = 0
if l <= m:
sum = sum + getsum(l, r, s, m, p * 2)
# 如果左儿子代表的区间 [s, m] 与询问区间有交集, 则递归查询左儿子
if r > m:
sum = sum + getsum(l, r, m + 1, t, p * 2 + 1)
# 如果右儿子代表的区间 [m + 1, t] 与询问区间有交集, 则递归查询右儿子
return sum
```
### 线段树的区间修改与懒惰标记
#### 过程
如果要求修改区间 $[l,r]$,把所有包含在区间 $[l,r]$ 中的节点都遍历一次、修改一次,时间复杂度无法承受。我们这里要引入一个叫做 **「懒惰标记」** 的东西。
懒惰标记,简单来说,就是通过延迟对节点信息的更改,从而减少可能不必要的操作次数。每次执行修改时,我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改,但不更新该节点的子节点的信息。实质性的修改则在下一次访问带有标记的节点时才进行。
仍然以最开始的图为例,我们将执行若干次给区间内的数加上一个值的操作。我们现在给每个节点增加一个 $t_i$,表示该节点带的标记值。
最开始时的情况是这样的(为了节省空间,这里不再展示每个节点管辖的区间):
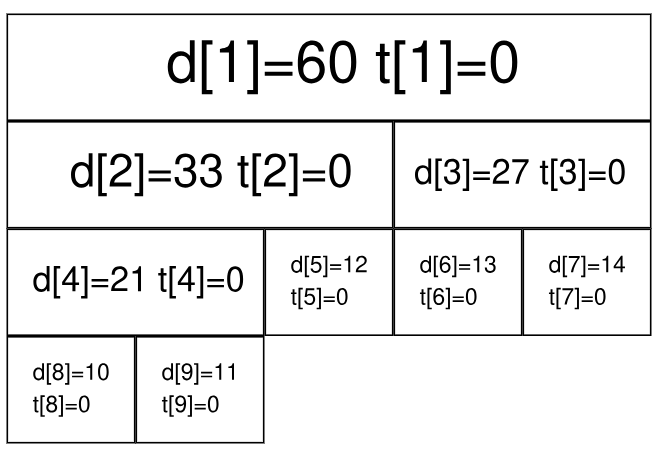
现在我们准备给 $[3,5]$ 上的每个数都加上 $5$。根据前面区间查询的经验,我们很快找到了两个极大区间 $[3,3]$ 和 $[4,5]$(分别对应线段树上的 $3$ 号点和 $5$ 号点)。
我们直接在这两个节点上进行修改,并给它们打上标记:

我们发现,$3$ 号节点的信息虽然被修改了(因为该区间管辖两个数,所以 $d_3$ 加上的数是 $5 \times 2=10$),但它的两个子节点却还没更新,仍然保留着修改之前的信息。不过不用担心,虽然修改目前还没进行,但当我们要查询这两个子节点的信息时,我们会利用标记修改这两个子节点的信息,使查询的结果依旧准确。
接下来我们查询一下 $[4,4]$ 区间上各数字的和。
我们通过递归找到 $[4,5]$ 区间,发现该区间并非我们的目标区间,且该区间上还存在标记。这时候就到标记下放的时间了。我们将该区间的两个子区间的信息更新,并清除该区间上的标记。
现在 $6$、$7$ 两个节点的值变成了最新的值,查询的结果也是准确的。
#### 实现
接下来给出在存在标记的情况下,区间修改和查询操作的参考实现。
区间修改(区间加上某个值):
=== "C++"
```cpp
void update(int l, int r, int c, int s, int t, int p) {
// [l, r] 为修改区间, c 为被修改的元素的变化量, [s, t] 为当前节点包含的区间, p
// 为当前节点的编号
if (l <= s && t <= r) {
d[p] += (t - s + 1) * c, b[p] += c;
return;
} // 当前区间为修改区间的子集时直接修改当前节点的值,然后打标记,结束修改
int m = s + ((t - s) >> 1);
if (b[p] && s != t) {
// 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值
d[p * 2] += b[p] * (m - s + 1), d[p * 2 + 1] += b[p] * (t - m);
b[p * 2] += b[p], b[p * 2 + 1] += b[p]; // 将标记下传给子节点
b[p] = 0; // 清空当前节点的标记
}
if (l <= m) update(l, r, c, s, m, p * 2);
if (r > m) update(l, r, c, m + 1, t, p * 2 + 1);
d[p] = d[p * 2] + d[p * 2 + 1];
}
```
```python
def update(l, r, c, s, t, p):
# [l, r] 为修改区间, c 为被修改的元素的变化量, [s, t] 为当前节点包含的区间, p
# 为当前节点的编号
if l <= s and t <= r:
d[p] = d[p] + (t - s + 1) * c
b[p] = b[p] + c
return
# 当前区间为修改区间的子集时直接修改当前节点的值, 然后打标记, 结束修改
m = s + ((t - s) >> 1)
if b[p] and s != t:
# 如果当前节点的懒标记非空, 则更新当前节点两个子节点的值和懒标记值
d[p * 2] = d[p * 2] + b[p] * (m - s + 1)
d[p * 2 + 1] = d[p * 2 + 1] + b[p] * (t - m)
# 将标记下传给子节点
b[p * 2] = b[p * 2] + b[p]
b[p * 2 + 1] = b[p * 2 + 1] + b[p]
# 清空当前节点的标记
b[p] = 0
if l <= m:
update(l, r, c, s, m, p * 2)
if r > m:
update(l, r, c, m + 1, t, p * 2 + 1)
d[p] = d[p * 2] + d[p * 2 + 1]
```
区间查询(区间求和):
```cpp
int getsum(int l, int r, int s, int t, int p) {
// [l, r] 为查询区间, [s, t] 为当前节点包含的区间, p 为当前节点的编号
if (l <= s && t <= r) return d[p];
// 当前区间为询问区间的子集时直接返回当前区间的和
int m = s + ((t - s) >> 1);
if (b[p]) {
// 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值
d[p * 2] += b[p] * (m - s + 1), d[p * 2 + 1] += b[p] * (t - m);
b[p * 2] += b[p], b[p * 2 + 1] += b[p]; // 将标记下传给子节点
b[p] = 0; // 清空当前节点的标记
}
int sum = 0;
if (l <= m) sum = getsum(l, r, s, m, p * 2);
if (r > m) sum += getsum(l, r, m + 1, t, p * 2 + 1);
return sum;
}
```
```python
def getsum(l, r, s, t, p):
# [l, r] 为查询区间, [s, t] 为当前节点包含的区间, p为当前节点的编号
if l <= s and t <= r:
return d[p]
# 当前区间为询问区间的子集时直接返回当前区间的和
m = s + ((t - s) >> 1)
if b[p]:
# 如果当前节点的懒标记非空, 则更新当前节点两个子节点的值和懒标记值
d[p * 2] = d[p * 2] + b[p] * (m - s + 1)
d[p * 2 + 1] = d[p * 2 + 1] + b[p] * (t - m)
# 将标记下传给子节点
b[p * 2] = b[p * 2] + b[p]
b[p * 2 + 1] = b[p * 2 + 1] + b[p]
# 清空当前节点的标记
b[p] = 0
sum = 0
if l <= m:
sum = getsum(l, r, s, m, p * 2)
if r > m:
sum = sum + getsum(l, r, m + 1, t, p * 2 + 1)
return sum
```
如果你是要实现区间修改为某一个值而不是加上某一个值的话,代码如下:
```cpp
void update(int l, int r, int c, int s, int t, int p) {
if (l <= s && t <= r) {
d[p] = (t - s + 1) * c, b[p] = c;
return;
}
int m = s + ((t - s) >> 1);
// 额外数组储存是否修改值
if (v[p]) {
d[p * 2] = b[p] * (m - s + 1), d[p * 2 + 1] = b[p] * (t - m);
b[p * 2] = b[p * 2 + 1] = b[p];
v[p * 2] = v[p * 2 + 1] = 1;
v[p] = 0;
}
if (l <= m) update(l, r, c, s, m, p * 2);
if (r > m) update(l, r, c, m + 1, t, p * 2 + 1);
d[p] = d[p * 2] + d[p * 2 + 1];
}
int getsum(int l, int r, int s, int t, int p) {
if (l <= s && t <= r) return d[p];
int m = s + ((t - s) >> 1);
if (v[p]) {
d[p * 2] = b[p] * (m - s + 1), d[p * 2 + 1] = b[p] * (t - m);
b[p * 2] = b[p * 2 + 1] = b[p];
v[p * 2] = v[p * 2 + 1] = 1;
v[p] = 0;
}
int sum = 0;
if (l <= m) sum = getsum(l, r, s, m, p * 2);
if (r > m) sum += getsum(l, r, m + 1, t, p * 2 + 1);
return sum;
}
```
```python
def update(l, r, c, s, t, p):
if l <= s and t <= r:
d[p] = (t - s + 1) * c
b[p] = c
return
m = s + ((t - s) >> 1)
if v[p]:
d[p * 2] = b[p] * (m - s + 1)
d[p * 2 + 1] = b[p] * (t - m)
b[p * 2] = b[p * 2 + 1] = b[p]
v[p * 2] = v[p * 2 + 1] = 1
v[p] = 0
if l <= m:
update(l, r, c, s, m, p * 2)
if r > m:
update(l, r, c, m + 1, t, p * 2 + 1)
d[p] = d[p * 2] + d[p * 2 + 1]
def getsum(l, r, s, t, p):
if l <= s and t <= r:
return d[p]
m = s + ((t - s) >> 1)
if v[p]:
d[p * 2] = b[p] * (m - s + 1)
d[p * 2 + 1] = b[p] * (t - m)
b[p * 2] = b[p * 2 + 1] = b[p]
v[p * 2] = v[p * 2 + 1] = 1
v[p] = 0
sum = 0
if l <= m:
sum = getsum(l, r, s, m, p * 2)
if r > m:
sum = sum + getsum(l, r, m + 1, t, p * 2 + 1)
return sum
```
### 动态开点线段树
前面讲到堆式储存的情况下,需要给线段树开 $4n$ 大小的数组。为了节省空间,我们可以不一次性建好树,而是在最初只建立一个根结点代表整个区间。当我们需要访问某个子区间时,才建立代表这个区间的子结点。这样我们不再使用 $2p$ 和 $2p+1$ 代表 $p$ 结点的儿子,而是用 $\text{ls}$ 和 $\text{rs}$ 记录儿子的编号。总之,动态开点线段树的核心思想就是:**结点只有在有需要的时候才被创建**。
单次操作的时间复杂度是不变的,为 $O(\log n)$。由于每次操作都有可能创建并访问全新的一系列结点,因此 $m$ 次单点操作后结点的数量规模是 $O(m\log n)$。最多也只需要 $2n-1$ 个结点,没有浪费。
单点修改:
```cpp
// root 表示整棵线段树的根结点;cnt 表示当前结点个数
int n, cnt, root;
int sum[n * 2], ls[n * 2], rs[n * 2];
// 用法:update(root, 1, n, x, f); 其中 x 为待修改节点的编号
void update(int& p, int s, int t, int x, int f) { // 引用传参
if (!p) p = ++cnt; // 当结点为空时,创建一个新的结点
if (s == t) {
sum[p] += f;
return;
}
int m = s + ((t - s) >> 1);
if (x <= m)
update(ls[p], s, m, x, f);
else
update(rs[p], m + 1, t, x, f);
sum[p] = sum[ls[p]] + sum[rs[p]]; // pushup
}
```
区间询问:
```cpp
// 用法:query(root, 1, n, l, r);
int query(int p, int s, int t, int l, int r) {
if (!p) return 0; // 如果结点为空,返回 0
if (s >= l && t <= r) return sum[p];
int m = s + ((t - s) >> 1), ans = 0;
if (l <= m) ans += query(ls[p], s, m, l, r);
if (r > m) ans += query(rs[p], m + 1, t, l, r);
return ans;
}
```
区间修改也是一样的,不过下放标记时要注意如果缺少孩子,就直接创建一个新的孩子。或者使用标记永久化技巧。
## 一些优化
这里总结几个线段树的优化:
- 在叶子节点处无需下放懒惰标记,所以懒惰标记可以不下传到叶子节点。
- 下放懒惰标记可以写一个专门的函数 `pushdown`,从儿子节点更新当前节点也可以写一个专门的函数 `maintain`(或者对称地用 `pushup`),降低代码编写难度。
- 标记永久化:如果确定懒惰标记不会在中途被加到溢出(即超过了该类型数据所能表示的最大范围),那么就可以将标记永久化。标记永久化可以避免下传懒惰标记,只需在进行询问时把标记的影响加到答案当中,从而降低程序常数。具体如何处理与题目特性相关,需结合题目来写。这也是树套树和可持久化数据结构中会用到的一种技巧。
## C++ 模板
??? "SegTreeLazyRangeAdd 可以区间加/求和的线段树模板"
```cpp
--8<-- "docs/ds/code/seg/seg_4.hpp
#include <bits/stdc++.h>
using namespace std;
template <typename T>
class SegTreeLazyRangeAdd {
vector<T> tree, lazy;
vector<T> *arr;
int n, root, n4, end;
void maintain(int cl, int cr, int p) {
int cm = cl + (cr - cl) / 2;
if (cl != cr && lazy[p]) {
lazy[p * 2] += lazy[p];
lazy[p * 2 + 1] += lazy[p];
tree[p * 2] += lazy[p] * (cm - cl + 1);
tree[p * 2 + 1] += lazy[p] * (cr - cm);
lazy[p] = 0;
}
}
T range_sum(int l, int r, int cl, int cr, int p) {
if (l <= cl && cr <= r) return tree[p];
int m = cl + (cr - cl) / 2;
T sum = 0;
maintain(cl, cr, p);
if (l <= m) sum += range_sum(l, r, cl, m, p * 2);
if (r > m) sum += range_sum(l, r, m + 1, cr, p * 2 + 1);
return sum;
}
void range_add(int l, int r, T val, int cl, int cr, int p) {
if (l <= cl && cr <= r) {
lazy[p] += val;
tree[p] += (cr - cl + 1) * val;
return;
}
int m = cl + (cr - cl) / 2;
maintain(cl, cr, p);
if (l <= m) range_add(l, r, val, cl, m, p * 2);
if (r > m) range_add(l, r, val, m + 1, cr, p * 2 + 1);
tree[p] = tree[p * 2] + tree[p * 2 + 1];
}
void build(int s, int t, int p) {
if (s == t) {
tree[p] = (*arr)[s];
return;
}
int m = s + (t - s) / 2;
build(s, m, p * 2);
build(m + 1, t, p * 2 + 1);
tree[p] = tree[p * 2] + tree[p * 2 + 1];
}
public:
explicit SegTreeLazyRangeAdd<T>(vector<T> v) {
n = v.size();
n4 = n * 4;
tree = vector<T>(n4, 0);
lazy = vector<T>(n4, 0);
arr = &v;
end = n - 1;
root = 1;
build(0, end, 1);
arr = nullptr;
}
void show(int p, int depth = 0) {
if (p > n4 || tree[p] == 0) return;
show(p * 2, depth + 1);
for (int i = 0; i < depth; ++i) putchar('\t');
printf("%d:%d\n", tree[p], lazy[p]);
show(p * 2 + 1, depth + 1);
}
T range_sum(int l, int r) { return range_sum(l, r, 0, end, root); }
void range_add(int l, int r, int val) { range_add(l, r, val, 0, end, root); }
};
```
??? "SegTreeLazyRangeSet 可以区间修改/求和的线段树模板"
```cpp
--8<-- "docs/ds/code/seg/seg_5.hpp"
#include <bits/stdc++.h>
using namespace std;
template <typename T>
class SegTreeLazyRangeSet {
vector<T> tree, lazy;
vector<T> *arr;
int n, root, n4, end;
void maintain(int cl, int cr, int p) {
int cm = cl + (cr - cl) / 2;
if (cl != cr && lazy[p]) {
lazy[p * 2] = lazy[p];
lazy[p * 2 + 1] = lazy[p];
tree[p * 2] = lazy[p] * (cm - cl + 1);
tree[p * 2 + 1] = lazy[p] * (cr - cm);
lazy[p] = 0;
}
}
T range_sum(int l, int r, int cl, int cr, int p) {
if (l <= cl && cr <= r) return tree[p];
int m = cl + (cr - cl) / 2;
T sum = 0;
maintain(cl, cr, p);
if (l <= m) sum += range_sum(l, r, cl, m, p * 2);
if (r > m) sum += range_sum(l, r, m + 1, cr, p * 2 + 1);
return sum;
}
void range_set(int l, int r, T val, int cl, int cr, int p) {
if (l <= cl && cr <= r) {
lazy[p] = val;
tree[p] = (cr - cl + 1) * val;
return;
}
int m = cl + (cr - cl) / 2;
maintain(cl, cr, p);
if (l <= m) range_set(l, r, val, cl, m, p * 2);
if (r > m) range_set(l, r, val, m + 1, cr, p * 2 + 1);
tree[p] = tree[p * 2] + tree[p * 2 + 1];
}
void build(int s, int t, int p) {
if (s == t) {
tree[p] = (*arr)[s];
return;
}
int m = s + (t - s) / 2;
build(s, m, p * 2);
build(m + 1, t, p * 2 + 1);
tree[p] = tree[p * 2] + tree[p * 2 + 1];
}
public:
explicit SegTreeLazyRangeSet<T>(vector<T> v) {
n = v.size();
n4 = n * 4;
tree = vector<T>(n4, 0);
lazy = vector<T>(n4, 0);
arr = &v;
end = n - 1;
root = 1;
build(0, end, 1);
arr = nullptr;
}
void show(int p, int depth = 0) {
if (p > n4 || tree[p] == 0) return;
show(p * 2, depth + 1);
for (int i = 0; i < depth; ++i) putchar('\t');
printf("%d:%d\n", tree[p], lazy[p]);
show(p * 2 + 1, depth + 1);
}
T range_sum(int l, int r) { return range_sum(l, r, 0, end, root); }
void range_set(int l, int r, int val) { range_set(l, r, val, 0, end, root); }
};
```
## 例题
???+ note "[luogu P3372【模板】线段树 1](https://www.luogu.com.cn/problem/P3372)"
已知一个数列,你需要进行下面两种操作:
- 将某区间每一个数加上 $k$。
- 求出某区间每一个数的和。
??? "参考代码"
```cpp
--8<-- "docs/ds/code/seg/seg_1.cpp"
#include <iostream>
typedef long long LL;
LL n, a[100005], d[270000], b[270000];
void build(LL l, LL r, LL p) { // l:鍖洪棿宸︾鐐?r:鍖洪棿鍙崇鐐?p:鑺傜偣鏍囧彿
if (l == r) {
d[p] = a[l]; // 灏嗚妭鐐硅祴鍊?
return;
}
LL m = l + ((r - l) >> 1);
build(l, m, p << 1), build(m + 1, r, (p << 1) | 1); // 鍒嗗埆寤虹珛瀛愭爲
d[p] = d[p << 1] + d[(p << 1) | 1];
}
void update(LL l, LL r, LL c, LL s, LL t, LL p) {
if (l <= s && t <= r) {
d[p] += (t - s + 1) * c, b[p] += c; // 濡傛灉鍖洪棿琚寘鍚簡锛岀洿鎺ュ緱鍑虹瓟妗?
return;
}
LL m = s + ((t - s) >> 1);
if (b[p])
d[p << 1] += b[p] * (m - s + 1), d[(p << 1) | 1] += b[p] * (t - m),
b[p << 1] += b[p], b[(p << 1) | 1] += b[p];
b[p] = 0;
if (l <= m)
update(l, r, c, s, m, p << 1); // 鏈鍜屼笅闈㈢殑涓€琛岀敤鏉ユ洿鏂皃*2鍜宲*2+1鐨勮妭鐐?
if (r > m) update(l, r, c, m + 1, t, (p << 1) | 1);
d[p] = d[p << 1] + d[(p << 1) | 1]; // 璁$畻璇ヨ妭鐐瑰尯闂村拰
}
LL getsum(LL l, LL r, LL s, LL t, LL p) {
if (l <= s && t <= r) return d[p];
LL m = s + ((t - s) >> 1);
if (b[p])
d[p << 1] += b[p] * (m - s + 1), d[(p << 1) | 1] += b[p] * (t - m),
b[p << 1] += b[p], b[(p << 1) | 1] += b[p];
b[p] = 0;
LL sum = 0;
if (l <= m)
sum =
getsum(l, r, s, m, p << 1); // 鏈鍜屼笅闈㈢殑涓€琛岀敤鏉ユ洿鏂皃*2鍜宲*2+1鐨勭瓟妗?
if (r > m) sum += getsum(l, r, m + 1, t, (p << 1) | 1);
return sum;
}
int main() {
std::ios::sync_with_stdio(0);
LL q, i1, i2, i3, i4;
std::cin >> n >> q;
for (LL i = 1; i <= n; i++) std::cin >> a[i];
build(1, n, 1);
while (q--) {
std::cin >> i1 >> i2 >> i3;
if (i1 == 2)
std::cout << getsum(i2, i3, 1, n, 1) << std::endl; // 鐩存帴璋冪敤鎿嶄綔鍑芥暟
else
std::cin >> i4, update(i2, i3, i4, 1, n, 1);
}
return 0;
}
```
???+ note "[luogu P3373【模板】线段树 2](https://www.luogu.com.cn/problem/P3373)"
已知一个数列,你需要进行下面三种操作:
- 将某区间每一个数乘上 $x$。
- 将某区间每一个数加上 $x$。
- 求出某区间每一个数的和。
??? "参考代码"
```cpp
--8<-- "docs/ds/code/seg/seg_2.cpp"
#include <cstdio>
#define ll long long
ll read() {
ll w = 1, q = 0;
char ch = ' ';
while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if (ch == '-') w = -1, ch = getchar();
while (ch >= '0' && ch <= '9') q = (ll)q * 10 + ch - '0', ch = getchar();
return (ll)w * q;
}
int n, m;
ll mod;
ll a[100005], sum[400005], mul[400005], laz[400005];
void up(int i) { sum[i] = (sum[(i << 1)] + sum[(i << 1) | 1]) % mod; }
void pd(int i, int s, int t) {
int l = (i << 1), r = (i << 1) | 1, mid = (s + t) >> 1;
if (mul[i] != 1) { // 鎳掓爣璁颁紶閫掞紝涓や釜鎳掓爣璁?
mul[l] *= mul[i];
mul[l] %= mod;
mul[r] *= mul[i];
mul[r] %= mod;
laz[l] *= mul[i];
laz[l] %= mod;
laz[r] *= mul[i];
laz[r] %= mod;
sum[l] *= mul[i];
sum[l] %= mod;
sum[r] *= mul[i];
sum[r] %= mod;
mul[i] = 1;
}
if (laz[i]) { // 鎳掓爣璁颁紶閫?
sum[l] += laz[i] * (mid - s + 1);
sum[l] %= mod;
sum[r] += laz[i] * (t - mid);
sum[r] %= mod;
laz[l] += laz[i];
laz[l] %= mod;
laz[r] += laz[i];
laz[r] %= mod;
laz[i] = 0;
}
return;
}
void build(int s, int t, int i) {
mul[i] = 1;
if (s == t) {
sum[i] = a[s];
return;
}
int mid = s + ((t - s) >> 1);
build(s, mid, i << 1); // 寤烘爲
build(mid + 1, t, (i << 1) | 1);
up(i);
}
void chen(int l, int r, int s, int t, int i, ll z) {
int mid = s + ((t - s) >> 1);
if (l <= s && t <= r) {
mul[i] *= z;
mul[i] %= mod; // 杩欐槸鍙栨ā鐨?
laz[i] *= z;
laz[i] %= mod; // 杩欐槸鍙栨ā鐨?
sum[i] *= z;
sum[i] %= mod; // 杩欐槸鍙栨ā鐨?
return;
}
pd(i, s, t);
if (mid >= l) chen(l, r, s, mid, (i << 1), z);
if (mid + 1 <= r) chen(l, r, mid + 1, t, (i << 1) | 1, z);
up(i);
}
void add(int l, int r, int s, int t, int i, ll z) {
int mid = s + ((t - s) >> 1);
if (l <= s && t <= r) {
sum[i] += z * (t - s + 1);
sum[i] %= mod; // 杩欐槸鍙栨ā鐨?
laz[i] += z;
laz[i] %= mod; // 杩欐槸鍙栨ā鐨?
return;
}
pd(i, s, t);
if (mid >= l) add(l, r, s, mid, (i << 1), z);
if (mid + 1 <= r) add(l, r, mid + 1, t, (i << 1) | 1, z);
up(i);
}
ll getans(int l, int r, int s, int t,
int i) { // 寰楀埌绛旀锛屽彲浠ョ湅涓嬩笂闈㈡噿鏍囪鍔╀簬鐞嗚В
int mid = s + ((t - s) >> 1);
ll tot = 0;
if (l <= s && t <= r) return sum[i];
pd(i, s, t);
if (mid >= l) tot += getans(l, r, s, mid, (i << 1));
tot %= mod;
if (mid + 1 <= r) tot += getans(l, r, mid + 1, t, (i << 1) | 1);
return tot % mod;
}
int main() { // 璇诲叆
int i, j, x, y, bh;
ll z;
n = read();
m = read();
mod = read();
for (i = 1; i <= n; i++) a[i] = read();
build(1, n, 1); // 寤烘爲
for (i = 1; i <= m; i++) {
bh = read();
if (bh == 1) {
x = read();
y = read();
z = read();
chen(x, y, 1, n, 1, z);
} else if (bh == 2) {
x = read();
y = read();
z = read();
add(x, y, 1, n, 1, z);
} else if (bh == 3) {
x = read();
y = read();
printf("%lld\n", getans(x, y, 1, n, 1));
}
}
return 0;
}
```
???+ note "[HihoCoder 1078 线段树的区间修改](https://cn.vjudge.net/problem/HihoCoder-1078)"
假设货架上从左到右摆放了 $N$ 种商品,并且依次标号为 $1$ 到 $N$,其中标号为 $i$ 的商品的价格为 $Pi$。小 Hi 的每次操作分为两种可能,第一种是修改价格:小 Hi 给出一段区间 $[L, R]$ 和一个新的价格 $\textit{NewP}$,所有标号在这段区间中的商品的价格都变成 $\textit{NewP}$。第二种操作是询问:小 Hi 给出一段区间 $[L, R]$,而小 Ho 要做的便是计算出所有标号在这段区间中的商品的总价格,然后告诉小 Hi。
??? "参考代码"
```cpp
--8<-- "docs/ds/code/seg/seg_3.cpp"
#include <iostream>
int n, a[100005], d[270000], b[270000];
void build(int l, int r, int p) { // 寤烘爲
if (l == r) {
d[p] = a[l];
return;
}
int m = l + ((r - l) >> 1);
build(l, m, p << 1), build(m + 1, r, (p << 1) | 1);
d[p] = d[p << 1] + d[(p << 1) | 1];
}
void update(int l, int r, int c, int s, int t,
int p) { // 鏇存柊锛屽彲浠ュ弬鑰冨墠闈袱涓緥棰?
if (l <= s && t <= r) {
d[p] = (t - s + 1) * c, b[p] = c;
return;
}
int m = s + ((t - s) >> 1);
if (b[p]) {
d[p << 1] = b[p] * (m - s + 1), d[(p << 1) | 1] = b[p] * (t - m);
b[p << 1] = b[(p << 1) | 1] = b[p];
b[p] = 0;
}
if (l <= m) update(l, r, c, s, m, p << 1);
if (r > m) update(l, r, c, m + 1, t, (p << 1) | 1);
d[p] = d[p << 1] + d[(p << 1) | 1];
}
int getsum(int l, int r, int s, int t, int p) { // 鍙栧緱绛旀锛屽拰鍓嶉潰涓€鏍?
if (l <= s && t <= r) return d[p];
int m = s + ((t - s) >> 1);
if (b[p]) {
d[p << 1] = b[p] * (m - s + 1), d[(p << 1) | 1] = b[p] * (t - m);
b[p << 1] = b[(p << 1) | 1] = b[p];
b[p] = 0;
}
int sum = 0;
if (l <= m) sum = getsum(l, r, s, m, p << 1);
if (r > m) sum += getsum(l, r, m + 1, t, (p << 1) | 1);
return sum;
}
int main() {
std::ios::sync_with_stdio(0);
std::cin >> n;
for (int i = 1; i <= n; i++) std::cin >> a[i];
build(1, n, 1);
int q, i1, i2, i3, i4;
std::cin >> q;
while (q--) {
std::cin >> i1 >> i2 >> i3;
if (i1 == 0)
std::cout << getsum(i2, i3, 1, n, 1) << std::endl;
else
std::cin >> i4, update(i2, i3, i4, 1, n, 1);
}
return 0;
}
```
???+ note "[2018 Multi-University Training Contest 5 Problem G. Glad You Came](https://vjudge.net/problem/HDU-6356)"
??? "解题思路"
维护一下每个区间的永久标记就可以了,最后在线段树上跑一边 DFS 统计结果即可。注意打标记的时候加个剪枝优化,否则会 TLE。
## 线段树合并
### 过程
顾名思义,线段树合并是指建立一棵新的线段树,这棵线段树的每个节点都是两棵原线段树对应节点合并后的结果。它常常被用于维护树上或是图上的信息。
显然,我们不可能真的每次建满一颗新的线段树,因此我们需要使用上文的动态开点线段树。
线段树合并的过程本质上相当暴力:
假设两颗线段树为 A 和 B,我们从 1 号节点开始递归合并。
递归到某个节点时,如果 A 树或者 B 树上的对应节点为空,直接返回另一个树上对应节点,这里运用了动态开点线段树的特性。
如果递归到叶子节点,我们合并两棵树上的对应节点。
最后,根据子节点更新当前节点并且返回。
???+ note "线段树合并的复杂度"
显然,对于两颗满的线段树,合并操作的复杂度是 $O(n\log n)$ 的。但实际情况下使用的常常是权值线段树,总点数和 $n$ 的规模相差并不大。并且合并时一般不会重复地合并某个线段树,所以我们最终增加的点数大致是 $n\log n$ 级别的。这样,总的复杂度就是 $O(n\log n)$ 级别的。当然,在一些情况下,可并堆可能是更好的选择。
### 实现
```cpp
int merge(int a, int b, int l, int r) {
if (!a) return b;
if (!b) return a;
if (l == r) {
// do something...
return a;
}
int mid = (l + r) >> 1;
tr[a].l = merge(tr[a].l, tr[b].l, l, mid);
tr[a].r = merge(tr[a].r, tr[b].r, mid + 1, r);
pushup(a);
return a;
}
```
### 例题
???+ note "[luogu P4556 \[Vani 有约会\] 雨天的尾巴/【模板】线段树合并](https://www.luogu.com.cn/problem/P4556)"
??? "解题思路"
线段树合并模板题,用差分把树上修改转化为单点修改,然后向上 dfs 线段树合并统计答案即可。
??? "参考代码"
```cpp
--8<-- "docs/ds/code/seg/seg_6.cpp"
#include <bits/stdc++.h>
using namespace std;
int n, fa[100005][22], dep[100005], rt[100005];
int sum[5000005], cnt = 0, res[5000005], ls[5000005], rs[5000005];
int m, ans[100005];
vector<int> v[100005];
void update(int x) {
if (sum[ls[x]] < sum[rs[x]]) {
res[x] = res[rs[x]];
sum[x] = sum[rs[x]];
} else {
res[x] = res[ls[x]];
sum[x] = sum[ls[x]];
}
}
int merge(int a, int b, int x, int y) {
if (!a) return b;
if (!b) return a;
if (x == y) {
sum[a] += sum[b];
return a;
}
int mid = (x + y) >> 1;
ls[a] = merge(ls[a], ls[b], x, mid);
rs[a] = merge(rs[a], rs[b], mid + 1, y);
update(a);
return a;
}
int add(int id, int x, int y, int co, int val) {
if (!id) id = ++cnt;
if (x == y) {
sum[id] += val;
res[id] = co;
return id;
}
int mid = (x + y) >> 1;
if (co <= mid)
ls[id] = add(ls[id], x, mid, co, val);
else
rs[id] = add(rs[id], mid + 1, y, co, val);
update(id);
return id;
}
void initlca(int x) {
for (int i = 0; i <= 20; i++) fa[x][i + 1] = fa[fa[x][i]][i];
for (int i : v[x]) {
if (i == fa[x][0]) continue;
dep[i] = dep[x] + 1;
fa[i][0] = x;
initlca(i);
}
}
int lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
for (int d = dep[x] - dep[y], i = 0; d; d >>= 1, i++)
if (d & 1) x = fa[x][i];
if (x == y) return x;
for (int i = 20; i >= 0; i--)
if (fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];
return fa[x][0];
}
void cacl(int x) {
for (int i : v[x]) {
if (i == fa[x][0]) continue;
cacl(i);
rt[x] = merge(rt[x], rt[i], 1, 100000);
}
ans[x] = res[rt[x]];
if (sum[rt[x]] == 0) ans[x] = 0;
}
int main() {
ios::sync_with_stdio(0);
cin >> n >> m;
for (int i = 0; i < n - 1; i++) {
int a, b;
cin >> a >> b;
v[a].push_back(b);
v[b].push_back(a);
}
initlca(1);
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
rt[a] = add(rt[a], 1, 100000, c, 1);
rt[b] = add(rt[b], 1, 100000, c, 1);
int t = lca(a, b);
rt[t] = add(rt[t], 1, 100000, c, -1);
rt[fa[t][0]] = add(rt[fa[t][0]], 1, 100000, c, -1);
}
cacl(1);
for (int i = 1; i <= n; i++) cout << ans[i] << endl;
return 0;
}
```
## 线段树分裂
### 过程
线段树分裂实质上是线段树合并的逆过程。线段树分裂只适用于有序的序列,无序的序列是没有意义的,常用在动态开点的权值线段树。
注意当分裂和合并都存在时,我们在合并的时候必须回收节点,以避免分裂时会可能出现节点重复占用的问题。
从一颗区间为 $[1,N]$ 的线段树中分裂出 $[l,r]$,建一颗新的树:
从 1 号结点开始递归分裂,当节点不存在或者代表的区间 $[s,t]$ 与 $[l,r]$ 没有交集时直接回溯。
当 $[s,t]$ 与 $[l,r]$ 有交集时需要开一个新结点。
当 $[s,t]$ 包含于 $[l,r]$ 时,需要将当前结点直接接到新的树下面,并把旧边断开。
???+ note "线段树分裂的复杂度"
可以发现被断开的边最多只会有 $\log n$ 条,所以最终每次分裂的时间复杂度就是 $O(\log n)$,相当于区间查询的复杂度。
### 实现
```cpp
void split(int &p, int &q, int s, int t, int l, int r) {
if (t < l || r < s) return;
if (!p) return;
if (l <= s && t <= r) {
q = p;
p = 0;
return;
}
if (!q) q = New();
int m = s + t >> 1;
if (l <= m) split(ls[p], ls[q], s, m, l, r);
if (m < r) split(rs[p], rs[q], m + 1, t, l, r);
push_up(p);
push_up(q);
}
```
### 例题
???+ note "[P5494【模板】线段树分裂](https://www.luogu.com.cn/problem/P5494)"
??? "解题思路"
线段树分裂模板题,将 $[x,y]$ 分裂出来。
- 将 $t$ 树合并入 $p$ 树:单次合并即可。
- $p$ 树中插入 $x$ 个 $q$:单点修改。
- 查询 $[x,y]$ 中数的个数:区间求和。
- 查询第 $k$ 小。
??? "参考代码"
```cpp
--8<-- "docs/ds/code/seg/seg_7.cpp"
#include <iostream>
using namespace std;
const int N = 2e5 + 10;
int n, m;
int idx = 1;
long long sum[N << 5];
int ls[N << 5], rs[N << 5], root[N << 2], rub[N << 5], cnt, tot;
//鍐呭瓨鍒嗛厤涓庡洖鏀?
int New() { return cnt ? rub[cnt--] : ++tot; }
void Del(int &p) {
ls[p] = rs[p] = sum[p] = 0;
rub[++cnt] = p;
p = 0;
}
void push_up(int p) { sum[p] = sum[ls[p]] + sum[rs[p]]; }
void build(int s, int t, int &p) {
if (!p) p = New();
if (s == t) {
cin >> sum[p];
return;
}
int m = s + t >> 1;
build(s, m, ls[p]);
build(m + 1, t, rs[p]);
push_up(p);
}
//鍗曠偣淇敼
void update(int x, int c, int s, int t, int &p) {
if (!p) p = New();
if (s == t) {
sum[p] += c;
return;
}
int m = s + t >> 1;
if (x <= m)
update(x, c, s, m, ls[p]);
else
update(x, c, m + 1, t, rs[p]);
push_up(p);
}
//鍚堝苟
int merge(int p, int q, int s, int t) {
if (!p || !q) return p + q;
if (s == t) {
sum[p] += sum[q];
Del(q);
return p;
}
int m = s + t >> 1;
ls[p] = merge(ls[p], ls[q], s, m);
rs[p] = merge(rs[p], rs[q], m + 1, t);
push_up(p);
Del(q);
return p;
}
//鍒嗚
void split(int &p, int &q, int s, int t, int l, int r) {
if (t < l || r < s) return;
if (!p) return;
if (l <= s && t <= r) {
q = p;
p = 0;
return;
}
if (!q) q = New();
int m = s + t >> 1;
if (l <= m) split(ls[p], ls[q], s, m, l, r);
if (m < r) split(rs[p], rs[q], m + 1, t, l, r);
push_up(p);
push_up(q);
}
long long query(int l, int r, int s, int t, int p) {
if (!p) return 0;
if (l <= s && t <= r) return sum[p];
int m = s + t >> 1;
long long ans = 0;
if (l <= m) ans += query(l, r, s, m, ls[p]);
if (m < r) ans += query(l, r, m + 1, t, rs[p]);
return ans;
}
int kth(int s, int t, int k, int p) {
if (s == t) return s;
int m = s + t >> 1;
long long left = sum[ls[p]];
if (k <= left)
return kth(s, m, k, ls[p]);
else
return kth(m + 1, t, k - left, rs[p]);
}
int main() {
cin >> n >> m;
build(1, n, root[1]);
while (m--) {
int op;
cin >> op;
if (!op) {
int p, x, y;
cin >> p >> x >> y;
split(root[p], root[++idx], 1, n, x, y);
} else if (op == 1) {
int p, t;
cin >> p >> t;
root[p] = merge(root[p], root[t], 1, n);
} else if (op == 2) {
int p, x, q;
cin >> p >> x >> q;
update(q, x, 1, n, root[p]);
} else if (op == 3) {
int p, x, y;
cin >> p >> x >> y;
cout << query(x, y, 1, n, root[p]) << endl;
} else {
int p, k;
cin >> p >> k;
if (sum[root[p]] < k)
cout << -1 << endl;
else
cout << kth(1, n, k, root[p]) << endl;
}
}
}
```
## 线段树优化建图[](https://oi-wiki.org/ds/seg/#%E7%BA%BF%E6%AE%B5%E6%A0%91%E4%BC%98%E5%8C%96%E5%BB%BA%E5%9B%BE "Permanent link")
在建图连边的过程中,我们有时会碰到这种题目,一个点向一段连续的区间中的点连边或者一个连续的区间向一个点连边,如果我们真的一条一条连过去,那一旦点的数量多了复杂度就爆炸了,这里就需要用线段树的区间性质来优化我们的建图了。
下面是一个线段树。
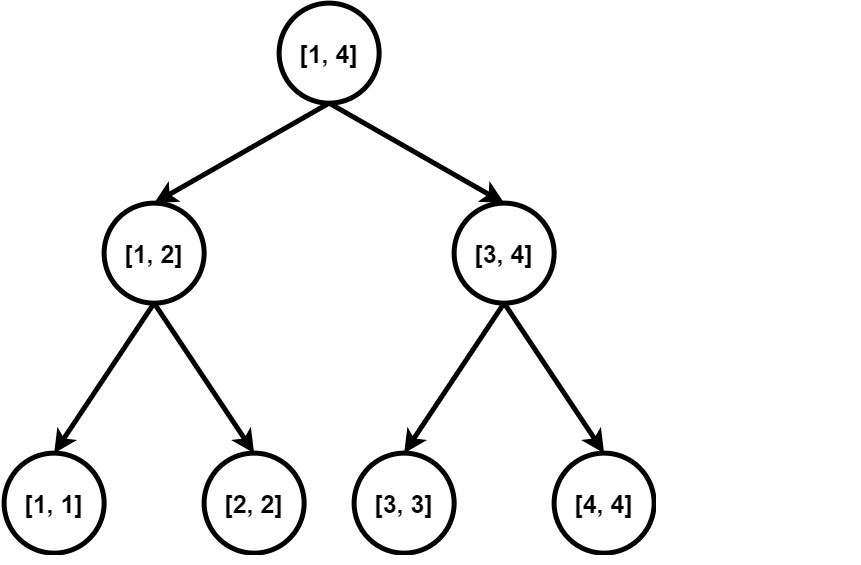
每个节点都代表了一个区间,假设我们要向区间 [2,4]  连边。
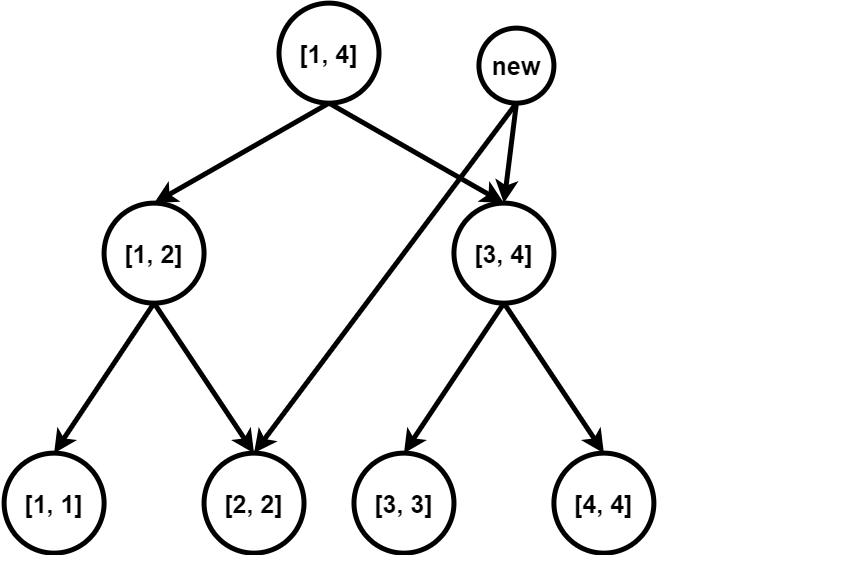
在一些题目中,还会出现一个区间连向一个点的情况,则我们将上面第一张图的有向边全部反过来即可,上面的树叫做入树,下面这个叫做出树。
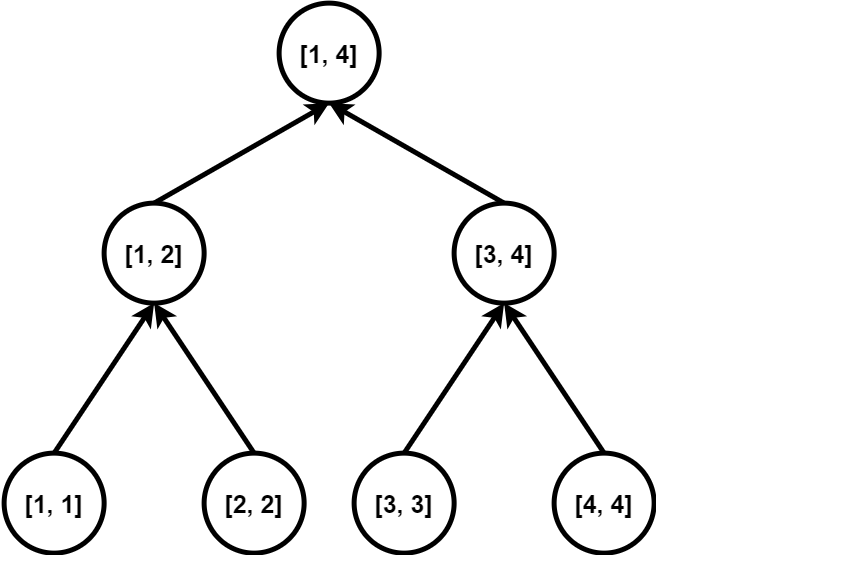
[Legacy](https://codeforces.com/problemset/problem/786/B)
题目大意:有  个点、 次操作。每一种操作为以下三种类型中的一种:

- 操作一:连一条  的有向边,权值为 。
- 操作二:对于所有  连一条  的有向边,权值为 。
- 操作三:对于所有  连一条  的有向边,权值为 。
求从点  到其他点的最短路。
。
```
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 1e5 + 5; using pil = pair<int, ll>; using pli = pair<ll, int>; int n, q, s, tot, rt1, rt2; int pos[N]; ll dis[N << 3]; vector<pil> e[N << 3]; bitset<(N << 3)> vis; struct seg { int l, r, lson, rson; } t[N << 3]; inline int ls(int u) { // 左儿子 return t[u].lson; } inline int rs(int u) { // 右儿子 return t[u].rson; } void build(int &u, int l, int r) { // 动态开点建造入树 u = ++tot; t[u] = seg{l, r}; if (l == r) { pos[l] = u; return; } int mid = (l + r) >> 1; build(t[u].lson, l, mid); build(t[u].rson, mid + 1, r); e[u].emplace_back(ls(u), 0); e[u].emplace_back(rs(u), 0); } void build2(int &u, int l, int r) { // 动态开点建造出树 if (l == r) { u = pos[l]; return; } u = ++tot; t[u] = seg{l, r}; int mid = (l + r) >> 1; build2(t[u].lson, l, mid); build2(t[u].rson, mid + 1, r); e[ls(u)].emplace_back(u, 0); e[rs(u)].emplace_back(u, 0); } void add1(int u, int lr, int rr, int v, ll w) { // 点向区间连边 if (lr <= t[u].l && t[u].r <= rr) { e[v].emplace_back(u, w); return; } int mid = (t[u].l + t[u].r) >> 1; if (lr <= mid) { add1(ls(u), lr, rr, v, w); } if (rr > mid) { add1(rs(u), lr, rr, v, w); } } void add2(int u, int lr, int rr, int v, ll w) { // 区间向点连边 if (lr <= t[u].l && t[u].r <= rr) { e[u].emplace_back(v, w); return; } int mid = (t[u].l + t[u].r) >> 1; if (lr <= mid) { add2(ls(u), lr, rr, v, w); } if (rr > mid) { add2(rs(u), lr, rr, v, w); } } void dij(int S) { priority_queue<pli, vector<pli>, greater<pli> > q; int tot = (n << 2); for (int i = 1; i <= tot; ++i) { dis[i] = 1e18; } dis[S] = 0; q.emplace(dis[S], S); while (!q.empty()) { pli fr = q.top(); q.pop(); int u = fr.second; if (vis[u]) continue; for (pil it : e[u]) { int v = it.first; ll w = it.second; if (dis[v] > dis[u] + w) { dis[v] = dis[u] + w; q.emplace(dis[v], v); } } } } int main() { scanf("%d%d%d", &n, &q, &s); build(rt1, 1, n); build2(rt2, 1, n); for (int i = 1, op, u; i <= q; ++i) { scanf("%d%d", &op, &u); if (op == 1) { int v; ll w; scanf("%d%lld", &v, &w); e[pos[u]].emplace_back(pos[v], w); } else if (op == 2) { int l, r; ll w; scanf("%d%d%lld", &l, &r, &w); add1(rt1, l, r, pos[u], w); } else { int l, r; ll w; scanf("%d%d%lld", &l, &r, &w); add2(rt2, l, r, pos[u], w); } } dij(pos[s]); for (int i = 1; i <= n; ++i) { if (dis[pos[i]] == 1e18) { printf("-1 "); } else { printf("%lld ", dis[pos[i]]); } } return 0; }
```
## 拓展 - 猫树[](https://oi-wiki.org/ds/seg/#%E6%8B%93%E5%B1%95---%E7%8C%AB%E6%A0%91 "Permanent link")
众所周知线段树可以支持高速查询某一段区间的信息和,比如区间最大子段和,区间和,区间矩阵的连乘积等等。
但是有一个问题在于普通线段树的区间询问在某些毒瘤的眼里可能还是有些慢了。
简单来说就是线段树建树的时候需要做 ") 次合并操作,而每一次区间询问需要做 ") 次合并操作,询问区间和这种东西的时候还可以忍受,但是当我们需要询问区间线性基这种合并复杂度高达 ") 的信息的话,此时就算是做 ") 次合并有些时候在时间上也是不可接受的。
而所谓「猫树」就是一种不支持修改,仅仅支持快速区间询问的一种静态线段树。
构造一棵这样的静态线段树需要 ") 次合并操作,但是此时的查询复杂度被加速至 ") 次合并操作。
在处理线性基这样特殊的信息的时候甚至可以将复杂度降至 ")。
### 原理[](https://oi-wiki.org/ds/seg/#%E5%8E%9F%E7%90%86 "Permanent link")
在查询  这段区间的信息和的时候,将线段树树上代表  的节点和代表  这段区间的节点在线段树上的 LCA 求出来,设这个节点  代表的区间为 ,我们会发现一些非常有趣的性质:
1.  这个区间一定包含 。显然,因为它既是  的祖先又是  的祖先。
2.  这个区间一定跨越  的中点。由于  是  和  的 LCA,这意味着  的左儿子是  的祖先而不是  的祖先, 的右儿子是  的祖先而不是  的祖先。因此, 一定在  这个区间内, 一定在  这个区间内。
有了这两个性质,我们就可以将询问的复杂度降至 ") 了。
### 实现[](https://oi-wiki.org/ds/seg/#%E5%AE%9E%E7%8E%B0_5 "Permanent link")
具体来讲我们建树的时候对于线段树树上的一个节点,设它代表的区间为 。
不同于传统线段树在这个节点里只保留  的和,我们在这个节点里面额外保存  的后缀和数组和  的前缀和数组。
这样的话建树的复杂度为 =2T(n/2)+O(n)=O(n\log{n})") 同理空间复杂度也从原来的 ") 变成了 ")。
下面是最关键的询问了。
如果我们询问的区间是  那么我们把代表  的节点和代表  的节点的 LCA 求出来,记为 。
根据刚才的两个性质, 在  所包含的区间之内并且一定跨越了  的中点。
这意味这一个非常关键的事实是我们可以使用  里面的前缀和数组和后缀和数组,将  拆成  从而拼出来  这个区间。
而这个过程仅仅需要 ") 次合并操作!
不过我们好像忽略了点什么?
似乎求 LCA 的复杂度似乎还不是 "),暴力求是 ") 的,倍增法则是 ") 的,转 ST 表的代价又太大……
### 堆式建树[](https://oi-wiki.org/ds/seg/#%E5%A0%86%E5%BC%8F%E5%BB%BA%E6%A0%91 "Permanent link")
具体来将我们将这个序列补成  的整次幂,然后建线段树。
此时我们发现线段树上两个节点的 LCA 编号,就是两个节点二进制编号的最长公共前缀 LCP。
稍作思考即可发现发现在  和  的二进制下 `lcp(x,y)=x>>log[x^y]`。
所以我们预处理一个 `log` 数组即可轻松完成求 LCA 的工作。
这样我们就构建了一个猫树。
由于建树的时候涉及到求前缀和和求后缀和,所以对于线性基这种虽然合并是 ") 但是求前缀和却是 ") 的信息,使用猫树可以将静态区间线性基从 ") 优化至 ") 的复杂度。
### 参考[](https://oi-wiki.org/ds/seg/#%E5%8F%82%E8%80%83 "Permanent link")
- [immortalCO 大爷的博客](https://immortalco.blog.uoj.ac/blog/2102)
- [[Kle77]](http://ieeexplore.ieee.org/document/1675628/) V. Klee, "Can the Measure of be Computed in Less than O (n log n) Steps?," Am. Math. Mon., vol. 84, no. 4, pp. 284–285, Apr. 1977.
- [[BeW80]](https://www.tandfonline.com/doi/full/10.1080/00029890.1977.11994336) Bentley and Wood, "An Optimal Worst Case Algorithm for Reporting Intersections of Rectangles," IEEE Trans. Comput., vol. C–29, no. 7, pp. 571–577, Jul. 1980.
---
> 本页面最近更新:2023/11/14 20:34:23,[更新历史](https://github.com/OI-wiki/OI-wiki/commits/master/docs/ds/seg.md)
> 发现错误?想一起完善? [在 GitHub 上编辑此页!](https://oi-wiki.org/edit-landing/?ref=/ds/seg.md "edit.link.title")
> 本页面贡献者:[ChungZH](https://github.com/ChungZH), [billchenchina](https://github.com/billchenchina), [Chrogeek](https://github.com/Chrogeek), [Early0v0](https://github.com/Early0v0), [ethan-enhe](https://github.com/ethan-enhe), [HeRaNO](https://github.com/HeRaNO), [hsfzLZH1](https://github.com/hsfzLZH1), [iamtwz](https://github.com/iamtwz), [Ir1d](https://github.com/Ir1d), [konnyakuxzy](https://github.com/konnyakuxzy), [luoguojie](https://github.com/luoguojie), [Marcythm](https://github.com/Marcythm), [orzAtalod](https://github.com/orzAtalod), [StudyingFather](https://github.com/StudyingFather), [wy-luke](https://github.com/wy-luke), [Xeonacid](https://github.com/Xeonacid), [CCXXXI](https://github.com/CCXXXI), [chenzheAya](https://github.com/chenzheAya), [CJSoft](https://github.com/CJSoft), [cjsoft](https://github.com/cjsoft), [countercurrent-time](https://github.com/countercurrent-time), [DawnMagnet](https://github.com/DawnMagnet), [Enter-tainer](https://github.com/Enter-tainer), [fafafa114](https://github.com/fafafa114), [GavinZhengOI](https://github.com/GavinZhengOI), [Haohu Shen](mailto:haohu.shen@ucalgary.ca), [Henry-ZHR](https://github.com/Henry-ZHR), [hjsjhn](https://github.com/hjsjhn), [hly1204](https://github.com/hly1204), [jaxvanyang](https://github.com/jaxvanyang), [Jebearssica](https://github.com/Jebearssica), [kenlig](https://github.com/kenlig), [ksyx](https://github.com/ksyx), [megakite](https://github.com/megakite), [Menci](https://github.com/Menci), [moon-dim](https://github.com/moon-dim), [NachtgeistW](https://github.com/NachtgeistW), [onelittlechildawa](https://github.com/onelittlechildawa), [ouuan](https://github.com/ouuan), [shadowice1984](https://github.com/shadowice1984), [shawlleyw](https://github.com/shawlleyw), [shuzhouliu](https://github.com/shuzhouliu), [SukkaW](https://github.com/SukkaW), [Tiphereth-A](https://github.com/Tiphereth-A), [Yakzamk](https://github.com/Yakzamk), [Ycrpro](https://github.com/Ycrpro), [yifan0305](https://github.com/yifan0305)
> 本页面的全部内容在 **[CC BY-SA 4.0](https://creativecommons.org/licenses/by-sa/4.0/deed.zh) 和 [SATA](https://github.com/zTrix/sata-license)** 协议之条款下提供,附加条款亦可能应用
Copyright © 2016 - 2024 OI Wiki Team
Made with [Material for MkDocs
](https://squidfunk.github.io/mkdocs-material/)
[最近更新:f9019aab, 2024-01-29](https://github.com/OI-wiki/OI-wiki)
## 拓展 - 猫树
众所周知线段树可以支持高速查询某一段区间的信息和,比如区间最大子段和,区间和,区间矩阵的连乘积等等。
但是有一个问题在于普通线段树的区间询问在某些毒瘤的眼里可能还是有些慢了。
简单来说就是线段树建树的时候需要做 $O(n)$ 次合并操作,而每一次区间询问需要做 $O(\log{n})$ 次合并操作,询问区间和这种东西的时候还可以忍受,但是当我们需要询问区间线性基这种合并复杂度高达 $O(\log^2{w})$ 的信息的话,此时就算是做 $O(\log{n})$ 次合并有些时候在时间上也是不可接受的。
而所谓「猫树」就是一种不支持修改,仅仅支持快速区间询问的一种静态线段树。
构造一棵这样的静态线段树需要 $O(n\log{n})$ 次合并操作,但是此时的查询复杂度被加速至 $O(1)$ 次合并操作。
在处理线性基这样特殊的信息的时候甚至可以将复杂度降至 $O(n\log^2{w})$。
### 原理
在查询 $[l,r]$ 这段区间的信息和的时候,将线段树树上代表 $[l,l]$ 的节点和代表 $[r,r]$ 这段区间的节点在线段树上的 LCA 求出来,设这个节点 $p$ 代表的区间为 $[L,R]$,我们会发现一些非常有趣的性质:
1. $[L,R]$ 这个区间一定包含 $[l,r]$。显然,因为它既是 $l$ 的祖先又是 $r$ 的祖先。
2. $[l,r]$ 这个区间一定跨越 $[L,R]$ 的中点。由于 $p$ 是 $l$ 和 $r$ 的 LCA,这意味着 $p$ 的左儿子是 $l$ 的祖先而不是 $r$ 的祖先,$p$ 的右儿子是 $r$ 的祖先而不是 $l$ 的祖先。因此,$l$ 一定在 $[L,\mathit{mid}]$ 这个区间内,$r$ 一定在 $(\mathit{mid},R]$ 这个区间内。
有了这两个性质,我们就可以将询问的复杂度降至 $O(1)$ 了。
### 实现
具体来讲我们建树的时候对于线段树树上的一个节点,设它代表的区间为 $(l,r]$。
不同于传统线段树在这个节点里只保留 $[l,r]$ 的和,我们在这个节点里面额外保存 $(l,\mathit{mid}]$ 的后缀和数组和 $(\mathit{mid},r]$ 的前缀和数组。
这样的话建树的复杂度为 $T(n)=2T(n/2)+O(n)=O(n\log{n})$ 同理空间复杂度也从原来的 $O(n)$ 变成了 $O(n\log{n})$。
下面是最关键的询问了。
如果我们询问的区间是 $[l,r]$ 那么我们把代表 $[l,l]$ 的节点和代表 $[r,r]$ 的节点的 LCA 求出来,记为 $p$。
根据刚才的两个性质,$l,r$ 在 $p$ 所包含的区间之内并且一定跨越了 $p$ 的中点。
这意味这一个非常关键的事实是我们可以使用 $p$ 里面的前缀和数组和后缀和数组,将 $[l,r]$ 拆成 $[l,\mathit{mid}]+(\mathit{mid},r]$ 从而拼出来 $[l,r]$ 这个区间。
而这个过程仅仅需要 $O(1)$ 次合并操作!
不过我们好像忽略了点什么?
似乎求 LCA 的复杂度似乎还不是 $O(1)$,暴力求是 $O(\log{n})$ 的,倍增法则是 $O(\log{\log{n}})$ 的,转 ST 表的代价又太大……
### 堆式建树
具体来将我们将这个序列补成 $2$ 的整次幂,然后建线段树。
此时我们发现线段树上两个节点的 LCA 编号,就是两个节点二进制编号的最长公共前缀 LCP。
稍作思考即可发现发现在 $x$ 和 $y$ 的二进制下 `lcp(x,y)=x>>log[x^y]`。
所以我们预处理一个 `log` 数组即可轻松完成求 LCA 的工作。
这样我们就构建了一个猫树。
由于建树的时候涉及到求前缀和和求后缀和,所以对于线性基这种虽然合并是 $O(\log^2{w})$ 但是求前缀和却是 $O(n\log{n})$ 的信息,使用猫树可以将静态区间线性基从 $O(n\log^2{w}+m\log^2{w}\log{n})$ 优化至 $O(n\log{n}\log{w}+m\log^2{w})$ 的复杂度。
### 参考
- [immortalCO 大爷的博客](https://immortalco.blog.uoj.ac/blog/2102)
- [\[Kle77\]](http://ieeexplore.ieee.org/document/1675628/) V. Klee, "Can the Measure of be Computed in Less than O (n log n) Steps?," Am. Math. Mon., vol. 84, no. 4, pp. 284–285, Apr. 1977.
- [\[BeW80\]](https://www.tandfonline.com/doi/full/10.1080/00029890.1977.11994336) Bentley and Wood, "An Optimal Worst Case Algorithm for Reporting Intersections of Rectangles," IEEE Trans. Comput., vol. C–29, no. 7, pp. 571–577, Jul. 1980.
@[toc]
我们在大学的教材上会学到一些基本的树结构,比如二叉树、二叉搜索树、AVL树、堆。但是这远远不够,在树的世界里,还有很多的奇技淫巧。
**RMQ**问题(`Range Minimum/Maximum Query`),求区间最大值或者最小值,类似的还有区间和问题;设有长度为 $n$ 的数列 $\{a_1,a_2, a_3,a_4,...,a_n\}$,需进行如下操作:
- 求最值:给定 $i,j \leq n$,求 $\{a_i,...,a_j\}$ 区间内的最值;
- 区间求和:给定 $1 \leq i,j \leq n$,求 $\{a_i,...,a_j\}$ 区间的和;
- 修改元素:给定 $k$ 和 $x$,把 $a_k$ 改成 $x$;
如果我们用数组存储数列,上面的操作中,求最值 $O(n)$,求和 $O(n)$,修改 $O(1)$,如果有 $m$ 次的修改元素+求和+求最值,那么总复杂度为 $O(mn)$。如果 $m$ 和 $n$ 太大,有 $100\ 000$ 以上,则整个程序的复杂度为 $10^{10}$ 的复杂度,太大了!
对于这样一类问题, 我们可以使用线段树,在 $O(m\log_2n)$ 的时间内解决。
---
## 一、线段树的概念
线段树是一种用于区间处理的数据结构,用二叉树构造。其中,树的每个结点代表一条线段 $[L, R]$:
对每个线段 $[L, R]$,$L$ 是左子节点,$R$ 是右子节点:
- $L=R$,说明这个结点只有一个点,就是一个叶子结点;
- $L \lt R$,说明这个结点代表的不止一个点,它有两个儿子,左儿子代表的区间 $[L,M]$,右儿子代表的区间 $[M+1,R]$,其中 $M = (L+R)/2$。
由于线段树是二叉树,一个区间每次折一半往下分,所以最多分 $logn$ 次到达最下层。需要查找一个结点或者区间时,顺着结点往下找,最多 $log_2n$ 次就可以找到。**线段树利用了折半查找的原理,因此效率很高。**
对于RMQ问题,线段树修改元素+查询最值可以分别在 $O(logn)$ 的时间内完成。 如下图,查询 $\{1,2,5,8,6,4,3\}$ 的最小值,其中每个结点上的值是这棵子树的最小值:
<div align="center">
<img src="https://img-blog.csdnimg.cn/20200330014026400.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L215UmVhbGl6YXRpb24=,size_16,color_FFFFFF,t_70" width="50%">
如果需要修改元素,**直接修改叶子结点上元素的值,然后从底部往上更新线段树**,操作次数也是 $O(log_2n)$。
总的来说,$m$ 次修改和查询的总复杂度为 $O(mlog_2n)$,即使对于 $n$ 为 $100\ 0000$ 的问题也能够**轻松解决**。
## 二、点修改
先来看看线段树中每次只修改一个点的问题。[POJ 2182 "Lost Cows"](),[解答]()。
@[toc]
# 线段树Segment Tree
## 一、线段树介绍
在竞赛题目中,线段树(区间树)是经常出现的一类题目。LeetCode上面也有线段树的问题。
普通的树是以一个个元素作为结点的,而**线段树是以一个个区间作为结点的**,它适用于对区间进行操作的题目。
一个很有意思的问题是——染色问题:$e.g.$ 对于一面墙,长度为 $n$,每次选择一段墙进行染色。有多次染色。$m$ 次操作后,我们可以看见多少种颜色?$m$ 次操作后,我们可以在 $[i, j]$ 区间中看见多少种颜色?
其实就是两种操作,染色操作(更新区间)和查询操作(查询区间)。我们很容易的想到可以用数组进行模拟,但是这样的话,这两种操作的复杂度就是 $O(n)$,$m$ 次就是 $O(mn)$。对于大数据的问题就无可奈何了。此时,线段树就大有用武之地了。
另一类问题是区间查询:$e.g.$ **如果我们不断的更新数据,然后对相应区间的和、最大值、最小值进行统计查询**。这种更新和查询有多次。对于这种区间的、动态的查询,用静态的数据结构很麻烦,**基于区间**的线段**树**是很有用的。
总结一下线段树的经典操作:
- 更新:更新区间中一个元素或者一个区间的值;
- 查询:查询一个区间中的最大值、最小值、区间和等等。
这两种操作都是 $O(logn)$的。同时,我们需要知道的是:**线段树面对的区间是固定的,我们不考虑添加新的元素。**
对于一个大小为 $8$ 的数组,我们可以构建如下的一棵树,叶节点就是每个元素——或者说长度为 $1$ 的区间,根节点则是整个区间:
<img src="https://img-blog.csdnimg.cn/20200326235927811.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L215UmVhbGl6YXRpb24=,size_16,color_FFFFFF,t_70" width = "60%">
以求和为例,要查询 $[4,7]$ 的区间和,我们一步就可以查询到了:
<img src="https://img-blog.csdnimg.cn/20200327000450455.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L215UmVhbGl6YXRpb24=,size_16,color_FFFFFF,t_70" width = "60%">
当然,不是所有的区间都可以直接得到,比如说查找 $[2,5]$ 的和,我们需要访问两个区间的和并相加,尽管如此,这比对整个区间进行操作仍然快得多。
<img src="https://img-blog.csdnimg.cn/2020032700065568.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L215UmVhbGl6YXRpb24=,size_16,color_FFFFFF,t_70" width="60%">
## 二、线段树基础实现
有一个结论:**线段树不一定是完全二叉树;但是线段树一定是平衡二叉树**。这样,**线段树就几乎不会出现最坏的情况,它不会退化成一个链表,这就是它的优势**。
为什么呢?原因很简单,我们每次将一个区间一分为二,两个区间的元素数量要么相等,要么相差 $1$ 个元素的数量,这样到叶子结点的时候,左右区间最多相差一层(多 $1$ 个元素的那边最后就深一层)。这符合平衡二叉树的定义。
虽然**线段树**不一定是完全二叉树,但是这样一棵平衡二叉树,我们仍然**可以使用数组来表示**,就将它看做一棵满二叉树,那些不存在的元素就当做 **空** 就行了。
尽然使用数组来表示,那么对于一棵满二叉树,有 $h$ 层,总结点数量是多少呢——$2^h-1$ 个结点。我们就将其作为 $2^h$,这样一定可以装下一棵满二叉树。同时,满二叉树最后一层有 $2^{h-1}$ 个结点,**大致等于前面所有的结点数量之和 $2^{h-1} - 1$ 。**
那么,如果区间有 $n$ 个元素,数组表示需要开多大的空间,需要多少个结点?**假设 $n = 2^k$,即最后一层的大小为 $2^k = n$**,那么根据前面的情况,此时我们存储整个二叉树,只需要 $2n$ 的空间。
当然,通常 $n$ 不一定等于 $2^k$,可能为 $2^{k+1}$,这意味着 $2n$ 的空间不一定能够存放叶子结点。最坏情况,叶子结点可能到达下一层,我们加一层,emmmm,假设为满二叉树,则**最后一层的结点数量大致等于前面所有的结点数量之和**,因此最后我们需要 $4n$ 的空间(前面的空间实际上有很大的富余),就可以存储所有的结点。
> 结论:$n$ 个元素的区间,构建线段树最大需要 $4n$ 的空间。
如果我们使用指针,可以完全避免这种浪费,平时可以这样实现,不过做题的时候用指针容易出错,因此建议用数组实现。
基础的代码如下:
```java
public class SegmentTree<E> {
private E[] data;
private E[] tree;
public SegmentTree(E[] arr) {
data = (E[])new Object[arr.length];
for (int i = 0; i < arr.length; ++i)
data[i] = arr[i];
tree = (E[])new Object[arr.length * 4];
buildSegmentTree(0, 0, data.length - 1); //treeIndex, l, r
}
public int getSize() {
return data.length;
}
public E get(int index) {
if (index < 0 || index >= data.length)
throw new IllegalArgumentException("Index is illegal.");
return data[index];
}
//返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子结点的索引
private int leftChild(int index) { //从0开始
return 2 * index + 1;
}
//返回一个索引所表示的左孩子的索引
private int rightChild(int index) {
return 2 * index + 2;
}
}
```
## 三、创建线段树(支持自定义逻辑)
用一个接口 `Merger<E>`,可以自定义两个区间“合并”的逻辑。
```java
public interface Merger<E> {
E merge(E a, E b); //将两个E转换为一个E返回去
}
```
代码如下:
```java
public class SegmentTree<E> {
private E[] data; //原始数据
private E[] tree;
private Merger<E> merger; //融合器
public SegmentTree(E[] arr, Merger<E> merger) {
data = (E[])new Object[arr.length];
for (int i = 0; i < arr.length; ++i)
data[i] = arr[i];
tree = (E[])new Object[arr.length * 4];
this.merger = merger;
buildSegmentTree(0, 0, data.length - 1); //treeIndex, l, r
}
private void buildSegmentTree(int treeIndex, int l, int r) {
if (l == r) { //只有一个元素时,创建叶子结点
tree[treeIndex] = data[l];
return;
}
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
int mid = l + (r - l) / 2;
buildSegmentTree(leftTreeIndex, l, mid); //先构建两棵子树
buildSegmentTree(rightTreeIndex, mid + 1, r);
//区间和就是用+; 最大值最小值就是max,min
//问题是E上面不一定定义了加法; 同时, 我们希望用户根据业务场景自由组合逻辑使用线段树
tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}
......
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append('[');
for (int i = 0; i < tree.length; ++i) {
if (tree[i] != null)
sb.append(tree[i]);
else
sb.append("null");
if (i != tree.length - 1) sb.append(' ');
}
return sb.toString();
}
}
```
## 四、线段树的区间查询
比如要在下面的线段树中查询一个区间 $[2,5]$,我们需要分别到左右两边的子树查询,并合并结果。
<img src="https://img-blog.csdnimg.cn/2020032700065568.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L215UmVhbGl6YXRpb24=,size_16,color_FFFFFF,t_70" width="60%">
事实上,区间查询是很简单的。由于每次我们都是将区间折半,因此我们很容易可以算出区间的 $[l, r]$ 以及 $mid$。如果我们要查询的区间 $target$ 在中轴 $mid$ 左边或者右边,就分别到两边的子树去查询;如果 $target$ 跨越了中轴,就需要同时到两边的子树查询。
$e.g.$ 查询 $[1,2]$:
- $[1,2]$ 的 $r = 2 \le 3(mid)$,到根节点 $A[0...7]$ 的左子树查询;
- $[1,2]$ 的 $l = 1 \le 1(mid)$,同时 $[1,2]$ 的 $r = 2 \gt 1(mid)$,因此同时向 $A[0...3]$ 的左子树查询 $[1,1]$,向右子树查询 $[2,2]$;
- $[1,1]$ 的 $l= 1\gt 0(mid)$,因此到 $A[0...1]$ 的右区间查询 $[1,1]$;$[2,2]$ 的 $r = 2 \le 2(mid)$,因此到 $A[2...3]$ 的左区间查询 $[2,2]$;
- 得到结果。
代码如下:
```java
//返回[queryL, queryR]区间的值
public E query(int queryL, int queryR) {
if (queryL < 0 || queryL >= data.length
|| queryR < 0 || queryR >= data.length || queryL > queryR)
throw new IllegalArgumentException("Index is illegal.");
//treeIndex, l, r, queryL, queryR
return query(0, 0, data.length - 1, queryL, queryR);
}
//在以treeindex为根的线段树[l...r]的范围中,搜索区间[queryL...queryR]的值
//区间范围也可以包装为一个内部类
private E query(int treeIndex, int l, int r, int queryL, int queryR) {
if (l == queryL && r == queryR) //是用户关注的区间
return tree[treeIndex];
int mid = l + (r - l) / 2;
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
if (queryL >= mid + 1) //用户关心的区间与左区间无关, 到右区间去查询
return query(rightTreeIndex, mid + 1, r, queryL, queryR);
else if (queryR <= mid) //用户关心的区间与右区间无关, 到左区间去查询
return query(leftTreeIndex, l, mid, queryL, queryR);
E leftResult = query(leftTreeIndex, l, mid, queryL, mid); //把用户关心的区间也分成两半
E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
return merger.merge(leftResult, rightResult); //两半区间融合用merger
}
//一个小小的测试用例
public static void main(String[] args) {
Integer[] nums = {-2, 0, 3, -5, 2, -1};
SegmentTree<Integer> segTree = new SegmentTree<>(nums, (a, b) -> a + b); //lambda表达式
System.out.println(segTree.query(0, 2)); //计算区间[1,2]的和-2+0+3=1
System.out.println(segTree.query(2, 5)); //-1
System.out.println(segTree.query(0, 5)); //-3从
}
```

---
## 五、线段树的点更新
修改元素,**直接修改叶子结点上元素的值,然后从底部往上更新线段树**,操作次数也是 $O(log_2n)$。
```java
//将index位置的元素更新为e
public void set(int index, E e) {
if (index < 0 || index >= data.length)
throw new IllegalArgumentException("Index is illegal.");
data[index] = e;
set(0, 0, data.length - 1, index, e); //treeIndex, l,r, index, e
}
//在以treeIndex为根的线段树中更新index的值为e
private void set(int treeIndex, int l, int r, int index, E e) {
if (l == r) { //直接修改叶子结点上元素的值
tree[treeIndex] = e;
return;
}
int mid = l + (r - l) / 2;
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
if (index >= mid + 1)
set(rightTreeIndex, mid + 1, r, index, e);
else //index <= mid
set(rightTreeIndex, l, mid, index, e);
//从底部往上更新线段树
tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]); //两半区间融合用merger
}
```
----
树形 DP,即在树上进行的 DP。由于树固有的递归性质,树形 DP 一般都是递归进行的。
## 基础
以下面这道题为例,介绍一下树形 DP 的一般过程。
???+ note " 例题 [洛谷 P1352 没有上司的舞会](https://www.luogu.com.cn/problem/P1352)"
某大学有 $n$ 个职员,编号为 $1 \sim N$。他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数 $a_i$,但是呢,如果某个职员的直接上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。
我们设 $f(i,0/1)$ 代表以 $i$ 为根的子树的最优解(第二维的值为 0 代表 $i$ 不参加舞会的情况,1 代表 $i$ 参加舞会的情况)。
对于每个状态,都存在两种决策(其中下面的 $x$ 都是 $i$ 的儿子):
- 上司不参加舞会时,下属可以参加,也可以不参加,此时有 $f(i,0) = \sum\max \{f(x,1),f(x,0)\}$;
- 上司参加舞会时,下属都不会参加,此时有 $f(i,1) = \sum{f(x,0)} + a_i$。
我们可以通过 DFS,在返回上一层时更新当前结点的最优解。
```cpp
#include <algorithm>
#include <cstdio>
using namespace std;
struct edge {
int v, next;
} e[6005];
int head[6005], n, cnt, f[6005][2], ans, is_h[6005], vis[6005];
void addedge(int u, int v) { // 建图
e[++cnt].v = v;
e[cnt].next = head[u];
head[u] = cnt;
}
void calc(int k) {
vis[k] = 1;
for (int i = head[k]; i; i = e[i].next) { // 枚举该结点的每个子结点
if (vis[e[i].v]) continue;
calc(e[i].v);
f[k][1] += f[e[i].v][0];
f[k][0] += max(f[e[i].v][0], f[e[i].v][1]); // 转移方程
}
return;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &f[i][1]);
for (int i = 1; i < n; i++) {
int l, k;
scanf("%d%d", &l, &k);
is_h[l] = 1;
addedge(k, l);
}
for (int i = 1; i <= n; i++)
if (!is_h[i]) { // 从根结点开始DFS
calc(i);
printf("%d", max(f[i][1], f[i][0]));
return 0;
}
}
```
### 习题
- [HDU 2196 Computer](https://vjudge.net/problem/HDU-2196)
- [POJ 1463 Strategic game](http://poj.org/problem?id=1463)
- [\[POI2014\]FAR-FarmCraft](https://www.luogu.com.cn/problem/P3574)
## 树上背包
树上的背包问题,简单来说就是背包问题与树形 DP 的结合。
???+ note " 例题 [洛谷 P2014 CTSC1997 选课](https://www.luogu.com.cn/problem/P2014)"
现在有 $n$ 门课程,第 $i$ 门课程的学分为 $a_i$,每门课程有零门或一门先修课,有先修课的课程需要先学完其先修课,才能学习该课程。
一位学生要学习 $m$ 门课程,求其能获得的最多学分数。
$n,m \leq 300$
每门课最多只有一门先修课的特点,与有根树中一个点最多只有一个父亲结点的特点类似。
因此可以想到根据这一性质建树,从而所有课程组成了一个森林的结构。为了方便起见,我们可以新增一门 $0$ 学分的课程(设这个课程的编号为 $0$),作为所有无先修课课程的先修课,这样我们就将森林变成了一棵以 $0$ 号课程为根的树。
我们设 $f(u,i,j)$ 表示以 $u$ 号点为根的子树中,已经遍历了 $u$ 号点的前 $i$ 棵子树,选了 $j$ 门课程的最大学分。
转移的过程结合了树形 DP 和 [背包 DP](./knapsack.md) 的特点,我们枚举 $u$ 点的每个子结点 $v$,同时枚举以 $v$ 为根的子树选了几门课程,将子树的结果合并到 $u$ 上。
记点 $x$ 的儿子个数为 $s_x$,以 $x$ 为根的子树大小为 $\textit{siz_x}$,可以写出下面的状态转移方程:
$$
f(u,i,j)=\max_{v,k \leq j,k \leq \textit{siz_v}} f(u,i-1,j-k)+f(v,s_v,k)
$$
注意上面状态转移方程中的几个限制条件,这些限制条件确保了一些无意义的状态不会被访问到。
$f$ 的第二维可以很轻松地用滚动数组的方式省略掉,注意这时需要倒序枚举 $j$ 的值。
可以证明,该做法的时间复杂度为 $O(nm)$[^note1]。
??? note "参考代码"
```cpp
#include <algorithm>
#include <cstdio>
#include <vector>
using namespace std;
int f[305][305], s[305], n, m;
vector<int> e[305];
int dfs(int u) {
int p = 1;
f[u][1] = s[u];
for (auto v : e[u]) {
int siz = dfs(v);
// 注意下面两重循环的上界和下界
// 只考虑已经合并过的子树,以及选的课程数超过 m+1 的状态没有意义
for (int i = min(p, m + 1); i; i--)
for (int j = 1; j <= siz && i + j <= m + 1; j++)
f[u][i + j] = max(f[u][i + j], f[u][i] + f[v][j]); // 转移方程
p += siz;
}
return p;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
int k;
scanf("%d%d", &k, &s[i]);
e[k].push_back(i);
}
dfs(0);
printf("%d", f[0][m + 1]);
return 0;
}
```
### 习题
- [「CTSC1997」选课](https://www.luogu.com.cn/problem/P2014)
- [「JSOI2018」潜入行动](https://loj.ac/problem/2546)
- [「SDOI2017」苹果树](https://loj.ac/problem/2268)
- [「Codeforces Round 875 Div. 1」Problem D. Mex Tree](https://codeforces.com/contest/1830/problem/D)
## 换根 DP
树形 DP 中的换根 DP 问题又被称为二次扫描,通常不会指定根结点,并且根结点的变化会对一些值,例如子结点深度和、点权和等产生影响。
通常需要两次 DFS,第一次 DFS 预处理诸如深度,点权和之类的信息,在第二次 DFS 开始运行换根动态规划。
接下来以一些例题来带大家熟悉这个内容。
???+ note " 例题 [\[POI2008\]STA-Station](https://www.luogu.com.cn/problem/P3478)"
给定一个 $n$ 个点的树,请求出一个结点,使得以这个结点为根时,所有结点的深度之和最大。
不妨令 $u$ 为当前结点,$v$ 为当前结点的子结点。首先需要用 $s_i$ 来表示以 $i$ 为根的子树中的结点个数,并且有 $s_u=1+\sum s_v$。显然需要一次 DFS 来计算所有的 $s_i$,这次的 DFS 就是预处理,我们得到了以某个结点为根时其子树中的结点总数。
考虑状态转移,这里就是体现"换根"的地方了。令 $f_u$ 为以 $u$ 为根时,所有结点的深度之和。
$f_v\leftarrow f_u$ 可以体现换根,即以 $u$ 为根转移到以 $v$ 为根。显然在换根的转移过程中,以 $v$ 为根或以 $u$ 为根会导致其子树中的结点的深度产生改变。具体表现为:
- 所有在 $v$ 的子树上的结点深度都减少了一,那么总深度和就减少了 $s_v$;
- 所有不在 $v$ 的子树上的结点深度都增加了一,那么总深度和就增加了 $n-s_v$;
根据这两个条件就可以推出状态转移方程 $f_v = f_u - s_v + n - s_v=f_u + n - 2 \times s_v$。
于是在第二次 DFS 遍历整棵树并状态转移 $f_v=f_u + n - 2 \times s_v$,那么就能求出以每个结点为根时的深度和了。最后只需要遍历一次所有根结点深度和就可以求出答案。
??? note "参考代码"
```cpp
#include <bits/stdc++.h>
using namespace std;
int head[1000010 << 1], tot;
long long n, sz[1000010], dep[1000010];
long long f[1000010];
struct node {
int to, next;
} e[1000010 << 1];
void add(int u, int v) { // 建图
e[++tot] = {v, head[u]};
head[u] = tot;
}
void dfs(int u, int fa) { // 预处理dfs
sz[u] = 1;
dep[u] = dep[fa] + 1;
for (int i = head[u]; i; i = e[i].next) {
int v = e[i].to;
if (v != fa) {
dfs(v, u);
sz[u] += sz[v];
}
}
}
void get_ans(int u, int fa) { // 第二次dfs换根dp
for (int i = head[u]; i; i = e[i].next) {
int v = e[i].to;
if (v != fa) {
f[v] = f[u] - sz[v] * 2 + n;
get_ans(v, u);
}
}
}
int main() {
scanf("%lld", &n);
int u, v;
for (int i = 1; i <= n - 1; i++) {
scanf("%d%d", &u, &v);
add(u, v);
add(v, u);
}
dfs(1, 1);
for (int i = 1; i <= n; i++) f[1] += dep[i];
get_ans(1, 1);
long long int ans = -1;
int id;
for (int i = 1; i <= n; i++) { // 统计答案
if (f[i] > ans) {
ans = f[i];
id = i;
}
}
printf("%d\n", id);
return 0;
}
```
### 习题
- [Atcoder Educational DP Contest, Problem V, Subtree](https://atcoder.jp/contests/dp/tasks/dp_v)
- [Educational Codeforces Round 67, Problem E, Tree Painting](https://codeforces.com/contest/1187/problem/E)
- [POJ 3585 Accumulation Degree](http://poj.org/problem?id=3585)
- [\[USACO10MAR\]Great Cow Gathering G](https://www.luogu.com.cn/problem/P2986)
- [CodeForce 708C Centroids](http://codeforces.com/problemset/problem/708/C)
## 参考资料与注释
[^note1]: [子树合并背包类型的 dp 的复杂度证明 - LYD729 的 CSDN 博客](https://blog.csdn.net/lyd_7_29/article/details/79854245)
---
author: greyqz, Ir1d, hsfzLZH1, huaruoji
分数规划用来求一个分式的极值。
形象一点就是,给出 $a_i$ 和 $b_i$,求一组 $w_i\in\{0,1\}$,最小化或最大化
$$
\displaystyle\frac{\sum\limits_{i=1}^na_i\times w_i}{\sum\limits_{i=1}^nb_i\times w_i}
$$
另外一种描述:每种物品有两个权值 $a$ 和 $b$,选出若干个物品使得 $\displaystyle\frac{\sum a}{\sum b}$ 最小/最大。
一般分数规划问题还会有一些奇怪的限制,比如『分母至少为 $W$』。
## 求解
### 二分法
分数规划问题的通用方法是二分。
假设我们要求最大值。二分一个答案 $mid$,然后推式子(为了方便少写了上下界):
$$
\displaystyle
\begin{aligned}
&\frac{\sum a_i\times w_i}{\sum b_i\times w_i}>mid\\
\Longrightarrow&\sum a_i\times w_i-mid\times \sum b_i\cdot w_i>0\\
\Longrightarrow&\sum w_i\times(a_i-mid\times b_i)>0
\end{aligned}
$$
那么只要求出不等号左边的式子的最大值就行了。如果最大值比 $0$ 要大,说明 $mid$ 是可行的,否则不可行。
求最小值的方法和求最大值的方法类似,读者不妨尝试着自己推一下。
### Dinkelbach 算法
Dinkelbach 算法的大概思想是每次用上一轮的答案当做新的 $L$ 来输入,不断地迭代,直至答案收敛。
***
分数规划的主要难点就在于如何求 $\displaystyle \sum w_i\times(a_i-mid\times b_i)$ 的最大值/最小值。下面通过一系列实例来讲解该式子的最大值/最小值的求法。
## 实例
### 模板
> 有 $n$ 个物品,每个物品有两个权值 $a$ 和 $b$。求一组 $w_i\in\{0,1\}$,最大化 $\displaystyle\frac{\sum a_i\times w_i}{\sum b_i\times w_i}$ 的值。
把 $a_i-mid\times b_i$ 作为第 $i$ 个物品的权值,贪心地选所有权值大于 $0$ 的物品即可得到最大值。
为了方便初学者理解,这里放上完整代码:
??? 参考代码
```cpp
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
using namespace std;
int read() {
int X = 0, w = 1;
char c = getchar();
while (c < '0' || c > '9') {
if (c == '-') w = -1;
c = getchar();
}
while (c >= '0' && c <= '9') X = X * 10 + c - '0', c = getchar();
return X * w;
}
const int N = 100000 + 10;
const double eps = 1e-6;
int n;
double a[N], b[N];
bool check(double mid) {
double s = 0;
for (int i = 1; i <= n; ++i)
if (a[i] - mid * b[i] > 0) // 如果权值大于 0
s += a[i] - mid * b[i]; // 选这个物品
return s > 0;
}
int main() {
// 输入
n = read();
for (int i = 1; i <= n; ++i) a[i] = read();
for (int i = 1; i <= n; ++i) b[i] = read();
// 二分
double L = 0, R = 1e9;
while (R - L > eps) {
double mid = (L + R) / 2;
if (check(mid)) // mid 可行,答案比 mid 大
L = mid;
else // mid 不可行,答案比 mid 小
R = mid;
}
// 输出
printf("%.6lf\n", L);
return 0;
}
```
***
为了节省篇幅,下面的代码只保留 `check` 部分。主程序和本题是类似的。
### [POJ2976 Dropping tests](http://poj.org/problem?id=2976)
> 有 $n$ 个物品,每个物品有两个权值 $a$ 和 $b$。
>
> 你可以选 $n-k$ 个物品 $p_1,p_2,\cdots,p_{n-k}$,使得 $\displaystyle\frac{\sum a_{p_i}}{\sum b_{p_i}}$ 最大。
>
> 输出答案乘 $100$ 后四舍五入到整数的值。
把第 $i$ 个物品的权值设为 $a_i-mid\times b_i$,然后选最大的 $n-k$ 个即可得到最大值。
```cpp
bool cmp(double x, double y) { return x > y; }
bool check(double mid) {
int s = 0;
for (int i = 1; i <= n; ++i) c[i] = a[i] - mid * b[i];
sort(c + 1, c + n + 1, cmp);
for (int i = 1; i <= n - k; ++i) s += c[i];
return s > 0;
}
```
### [洛谷 4377 Talent Show](https://www.luogu.com.cn/problem/P4377)
> 有 $n$ 个物品,每个物品有两个权值 $a$ 和 $b$。
>
> 你需要确定一组 $w_i\in\{0,1\}$,使得 $\displaystyle\frac{\sum w_i\times a_i}{\sum w_i\times b_i}$ 最大。
>
> 要求 $\displaystyle\sum w_i\times b_i \geq W$。
本题多了分母至少为 $W$ 的限制,因此无法再使用上一题的贪心算法。
可以考虑 01 背包。把 $b_i$ 作为第 $i$ 个物品的重量,$a_i-mid\times b_i$ 作为第 $i$ 个物品的价值,然后问题就转化为背包了。
那么 $dp[n][W]$ 就是最大值。
一个要注意的地方:$\sum w_i\times b_i$ 可能超过 $W$,此时直接视为 $W$ 即可。(想一想,为什么?)
```cpp
double f[1010];
bool check(double mid) {
for (int i = 1; i <= W; i++) f[i] = -1e9;
for (int i = 1; i <= n; i++)
for (int j = W; j >= 0; j--) {
int k = min(W, j + b[i]);
f[k] = max(f[k], f[j] + a[i] - mid * b[i]);
}
return f[W] > 0;
}
```
### [POJ2728 Desert King](http://poj.org/problem?id=2728)
> 每条边有两个权值 $a_i$ 和 $b_i$,求一棵生成树 $T$ 使得 $\displaystyle\frac{\sum_{e\in T}a_e}{\sum_{e\in T}b_e}$ 最小。
把 $a_i-mid\times b_i$ 作为每条边的权值,那么最小生成树就是最小值,
代码就是求最小生成树,我就不放代码了。
### [\[HNOI2009\] 最小圈](https://www.luogu.com.cn/problem/P3199)
> 每条边的边权为 $w$,求一个环 $C$ 使得 $\displaystyle\frac{\sum_{e\in C}w}{|C|}$ 最小。
把 $a_i-mid$ 作为边权,那么权值最小的环就是最小值。
因为我们只需要判最小值是否小于 $0$,所以只需要判断图中是否存在负环即可。
另外本题存在一种复杂度 $O(nm)$ 的算法,如果有兴趣可以阅读 [这篇文章](https://www.cnblogs.com/y-clever/p/7043553.html)。
```cpp
int SPFA(int u, double mid) { // 判负环
vis[u] = 1;
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].v;
double w = e[i].w - mid;
if (dis[u] + w < dis[v]) {
dis[v] = dis[u] + w;
if (vis[v] || SPFA(v, mid)) return 1;
}
}
vis[u] = 0;
return 0;
}
bool check(double mid) { // 如果有负环返回 true
for (int i = 1; i <= n; ++i) dis[i] = 0, vis[i] = 0;
for (int i = 1; i <= n; ++i)
if (SPFA(i, mid)) return 1;
return 0;
}
```
## 总结
分数规划问题是一类既套路又灵活的题目,一般使用二分解决。
分数规划问题的主要难点在于推出式子后想办法求出 $\displaystyle\sum w_i\times(a_i-mid\times b_i)$ 的最大值/最小值,而这个需要具体情况具体分析。
## 习题
- [JSOI2016 最佳团体](https://loj.ac/problem/2071)
- [SDOI2017 新生舞会](https://loj.ac/problem/2003)
- [UVa1389 Hard Life](https://www.luogu.com.cn/problem/UVA1389)
---
本页面将介绍 CDQ 分治。
## 简介
CDQ 分治是一种思想而不是具体的算法,与 [动态规划](../dp/index.md) 类似。目前这个思想的拓展十分广泛,依原理与写法的不同,大致分为三类:
- 解决和点对有关的问题。
- 1D 动态规划的优化与转移。
- 通过 CDQ 分治,将一些动态问题转化为静态问题。
CDQ 分治的思想最早由 IOI2008 金牌得主陈丹琦在高中时整理并总结,它也因此得名。[^ref1]
## 解决和点对有关的问题
这类问题多数类似于「给定一个长度为 n 的序列,统计有一些特性的点对 $(i,j)$ 的数量/找到一对点 $(i,j)$ 使得一些函数的值最大」。
CDQ 分治解决这类问题的算法流程如下:
1. 找到这个序列的中点 $mid$;
2. 将所有点对 $(i,j)$ 划分为 3 类:
1. $1 \leq i \leq mid,1 \leq j \leq mid$ 的点对;
2. $1 \leq i \leq mid ,mid+1 \leq j \leq n$ 的点对;
3. $mid+1 \leq i \leq n,mid+1 \leq j \leq n$ 的点对。
3. 将 $(1,n)$ 这个序列拆成两个序列 $(1,mid)$ 和 $(mid+1,n)$。此时第一类点对和第三类点对都在这两个序列之中;
4. 递归地处理这两类点对;
5. 设法处理第二类点对。
可以看到 CDQ 分治的思想就是不断地把点对通过递归的方式分给左右两个区间。
在实际应用时,我们通常使用一个函数 `solve(l,r)` 处理 $l \leq i \leq r,l \leq j \leq r$ 的点对。上述算法流程中的递归部分便是通过 `solve(l,mid)` 与 `solve(mid,r)` 来实现的。剩下的第二类点对则需要额外设计算法解决。
### 例题
???+ note "[三维偏序](https://www.luogu.com.cn/problem/P3810)"
给定一个序列,每个点有 $a_i,b_i,c_i$ 三个属性,试求:这个序列里有多少对点对 $(i,j)$ 满足 $a_j \leq a_i$ 且 $b_j \leq b_i$ 且 $c_j \leq c_i$ 且 $j \ne i$。
??? 解题思路
三维偏序是 CDQ 分治的经典问题。
题目要求统计序列里点对的个数,那试一下用 CDQ 分治。
首先将序列按 $a$ 排序。
假设我们现在写好了 `solve(l,r)`,并且通过递归搞定了 `solve(l,mid)` 和 `solve(mid+1,r)`。现在我们要做的,就是统计满足 $l \leq i \leq mid$,$mid+1 \leq j \leq r$ 的点对 $(i,j)$ 中,有多个点对还满足 $a_{i}<a_{j}$,$b_{i}<b_{j}$,$c_{i}<c_{j}$ 的限制条件。
稍微思考一下就会发现,那个 $a_{i}<a_{j}$ 的限制条件没啥用了:已经将序列按 $a$ 排序,则 $a_{i} < a_{j}$ 可转化为 $i < j$。既然 $i$ 比 $mid$ 小,$j$ 比 $mid$ 大,那 $i$ 肯定比 $j$ 要小。现在还剩下两个限制条件:$b_{i}<b_{j}$ 与 $c_{i}<c_{j}$, 根据这个限制条件我们就可以枚举 $j$, 求出有多少个满足条件的 $i$。
为了方便枚举,我们把 $(l,mid)$ 和 $(mid+1,r)$ 中的点全部按照 $b$ 的值从小到大排个序。之后我们依次枚举每一个 $j$, 把所有 $b_{i}<b_{j}$ 的点 $i$ 全部插入到某种数据结构里(这里我们选择 [树状数组](../ds/fenwick.md))。此时只要查询树状数组里有多少个点的 $c$ 值是小于 $c_{j}$ 的,我们就求出了对于这个点 $j$,有多少个 $i$ 可以合法匹配它了。
当我们插入一个 $c$ 值等于 $x$ 的点时,我们就令树状数组的 $x$ 这个位置单点 + 1,而查询树状数组里有多少个点小于 $x$ 的操作实际上就是在求 [前缀和](../basic/prefix-sum.md),只要我们事先对于所有的 $c$ 值做了 [离散化](../misc/discrete.md),我们的复杂度就是对的。
对于每一个 $j$,我们都需要将所有 $b_{i}<b_{j}$ 的点 $i$ 插入树状数组中。由于所有的 $i$ 和 $j$ 都已事先按照 $b$ 值排好序,这样的话只要以双指针的方式在树状数组里插入点,则对树状数组的插入操作就能从 $O(n^2)$ 次降到 $O(n)$ 次。
通过这样一个算法流程,我们就用 $O(n\log n)$ 的时间处理完了关于第二类点对的信息了。此时算法的时间复杂度是 $T(n)=T(\lfloor \frac{n}{2} \rfloor)+T(\lceil \frac{n}{2} \rceil)+O(n\log n)=O(n\log^2n)$。
??? 示例代码
```cpp
--8<-- "docs/misc/code/cdq-divide/cdq-divide_1.cpp"
#include <algorithm>
#include <cstdio>
const int maxN = 1e5 + 10;
const int maxK = 2e5 + 10;
int n, k;
struct Element {
int a, b, c;
int cnt;
int res;
bool operator!=(Element other) {
if (a != other.a) return true;
if (b != other.b) return true;
if (c != other.c) return true;
return false;
}
};
Element e[maxN];
Element ue[maxN];
int m, t;
int res[maxN];
struct BinaryIndexedTree {
int node[maxK];
int lowbit(int x) { return x & -x; }
void Add(int pos, int val) {
while (pos <= k) {
node[pos] += val;
pos += lowbit(pos);
}
return;
}
int Ask(int pos) {
int res = 0;
while (pos) {
res += node[pos];
pos -= lowbit(pos);
}
return res;
}
} BIT;
bool cmpA(Element x, Element y) {
if (x.a != y.a) return x.a < y.a;
if (x.b != y.b) return x.b < y.b;
return x.c < y.c;
}
bool cmpB(Element x, Element y) {
if (x.b != y.b) return x.b < y.b;
return x.c < y.c;
}
void CDQ(int l, int r) {
if (l == r) return;
int mid = (l + r) / 2;
CDQ(l, mid);
CDQ(mid + 1, r);
std::sort(ue + l, ue + mid + 1, cmpB);
std::sort(ue + mid + 1, ue + r + 1, cmpB);
int i = l;
int j = mid + 1;
while (j <= r) {
while (i <= mid && ue[i].b <= ue[j].b) {
BIT.Add(ue[i].c, ue[i].cnt);
i++;
}
ue[j].res += BIT.Ask(ue[j].c);
j++;
}
for (int k = l; k < i; k++) BIT.Add(ue[k].c, -ue[k].cnt);
return;
}
int main() {
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++) scanf("%d%d%d", &e[i].a, &e[i].b, &e[i].c);
std::sort(e + 1, e + n + 1, cmpA);
for (int i = 1; i <= n; i++) {
t++;
if (e[i] != e[i + 1]) {
m++;
ue[m].a = e[i].a;
ue[m].b = e[i].b;
ue[m].c = e[i].c;
ue[m].cnt = t;
t = 0;
}
}
CDQ(1, m);
for (int i = 1; i <= m; i++) res[ue[i].res + ue[i].cnt - 1] += ue[i].cnt;
for (int i = 0; i < n; i++) printf("%d\n", res[i]);
return 0;
}
```
***
???+ note "[CQOI2011 动态逆序对](https://www.luogu.com.cn/problem/P3157)"
对于序列 $a$,它的逆序对数定义为集合 $\{(i,j)| i<j \wedge a_i > a_j \}$ 中的元素个数。
现在给出 $1\sim n$ 的一个排列,按照某种顺序依次删除 $m$ 个元素,你的任务是在每次删除一个元素之前统计整个序列的逆序对数。
??? 示例代码
```cpp
--8<-- "docs/misc/code/cdq-divide/cdq-divide_2.cpp"
// 仔细推一下就是和三维偏序差不多的式子了,基本就是一个三维偏序的板子
#include <algorithm>
#include <cstdio>
using namespace std;
typedef long long ll;
int n;
int m;
struct treearray {
int ta[200010];
void ub(int& x) { x += x & (-x); }
void db(int& x) { x -= x & (-x); }
void c(int x, int t) {
for (; x <= n + 1; ub(x)) ta[x] += t;
}
int sum(int x) {
int r = 0;
for (; x > 0; db(x)) r += ta[x];
return r;
}
} ta;
struct data_ {
int val;
int del;
int ans;
} a[100010];
int rv[100010];
ll res;
bool cmp1(const data_& a, const data_& b) {
return a.val < b.val;
} // 重写两个比较
bool cmp2(const data_& a, const data_& b) { return a.del < b.del; }
void solve(int l, int r) { // 底下是具体的式子,套用
if (r - l == 1) {
return;
}
int mid = (l + r) / 2;
solve(l, mid);
solve(mid, r);
int i = l + 1;
int j = mid + 1;
while (i <= mid) {
while (a[i].val > a[j].val && j <= r) {
ta.c(a[j].del, 1);
j++;
}
a[i].ans += ta.sum(m + 1) - ta.sum(a[i].del);
i++;
}
i = l + 1;
j = mid + 1;
while (i <= mid) {
while (a[i].val > a[j].val && j <= r) {
ta.c(a[j].del, -1);
j++;
}
i++;
}
i = mid;
j = r;
while (j > mid) {
while (a[j].val < a[i].val && i > l) {
ta.c(a[i].del, 1);
i--;
}
a[j].ans += ta.sum(m + 1) - ta.sum(a[j].del);
j--;
}
i = mid;
j = r;
while (j > mid) {
while (a[j].val < a[i].val && i > l) {
ta.c(a[i].del, -1);
i--;
}
j--;
}
sort(a + l + 1, a + r + 1, cmp1);
return;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i].val);
rv[a[i].val] = i;
}
for (int i = 1; i <= m; i++) {
int p;
scanf("%d", &p);
a[rv[p]].del = i;
}
for (int i = 1; i <= n; i++) {
if (a[i].del == 0) a[i].del = m + 1;
}
for (int i = 1; i <= n; i++) {
res += ta.sum(n + 1) - ta.sum(a[i].val);
ta.c(a[i].val, 1);
}
for (int i = 1; i <= n; i++) {
ta.c(a[i].val, -1);
}
solve(0, n);
sort(a + 1, a + n + 1, cmp2);
for (int i = 1; i <= m; i++) {
printf("%lld\n", res);
res -= a[i].ans;
}
return 0;
}
```
## CDQ 分治优化 1D/1D 动态规划的转移
1D/1D 动态规划指的是一类特定的 DP 问题,该类题目的特征是 DP 数组是一维的,转移是 $O(n)$ 的。如果条件良好的话,有时可以通过 CDQ 分治来把它们的时间复杂度由 $O(n^2)$ 降至 $O(n\log^2n)$。
例如,给定一个序列,每个元素有两个属性 $a$,$b$。我们希望计算一个 DP 式子的值,它的转移方程如下:
$dp_{i}=1+ \max_{j=1}^{i-1}dp_{j}[a_{j}<a_{i}][b_{j}<b_{i}]$
这是一个二维最长上升子序列的 DP 方程,即只有 $j<i,a_{j}<a_{i}$,$b_{j}<b_{i}$ 的点 $j$ 可以更新点 $i$ 的 DP 值。
直接转移显然是 $O(n^2)$ 的。以下是使用 CDQ 分治优化转移过程的讲解。
我们发现 $dp_{j}$ 转移到 $dp_{i}$ 这种转移关系也是一种点对间的关系,所以我们用类似 CDQ 分治处理点对关系的方式来处理它。
这个转移过程相对来讲比较套路。假设现在正在处理的区间是 $(l,r)$,算法流程大致如下:
1. 如果 $l=r$,说明 $dp_{r}$ 值已经被计算好了。直接令 $dp_{r}++$ 然后返回即可;
2. 递归使用 `solve(l,mid)`;
3. 处理所有 $l \leq j \leq mid$,$mid+1 \leq i \leq r$ 的转移关系;
4. 递归使用 `solve(mid+1,r)`。
第三步的做法与 CDQ 分治求三维偏序差不多。处理 $l \leq j \leq mid$,$mid+1 \leq i \leq r$ 的转移关系的时候,我们会发现已经不用管 $j<i$ 这个限制条件了。因此,我们依然先将所有的点 $i$ 和点 $j$ 按 $a$ 值进行排序处理,然后用双指针的方式将 $j$ 点插入到树状数组里,最后查一下前缀最大值更新一下 $dp_{i}$ 就可以了。
### 转移过程的正确性证明
该 CDQ 写法和处理点对间关系的 CDQ 写法最大的不同就是处理 $l \leq j \leq mid$,$mid+1 \leq i \leq r$ 的点对这一部分。处理点对间关系的 CDQ 写法中,这一部分放到哪里都是可以的。但是,在用 CDQ 分治优化 DP 的时候,这个流程却必须夹在 $solve(l,mid)$,$solve(mid+1,r)$ 的中间。原因是 DP 的转移是 **有序的**,它必须满足两个条件,否则就是不对的:
1. 用来计算 $dp_{i}$ 的所有 $dp_{j}$ 值都必须是已经计算完毕的,不能存在「半成品」;
2. 用来计算 $dp_{i}$ 的所有 $dp_{j}$ 值都必须能更新到 $dp_{i}$,不能存在没有更新到的 $dp_{j}$ 值。
上述两个条件可能在 $O(n^2)$ 暴力的时候是相当容易满足的,但是使用 CDQ 分治后,转移顺序很显然已经乱掉了,所以有必要考察转移的正确性。
CDQ 分治的递归树如下所示。
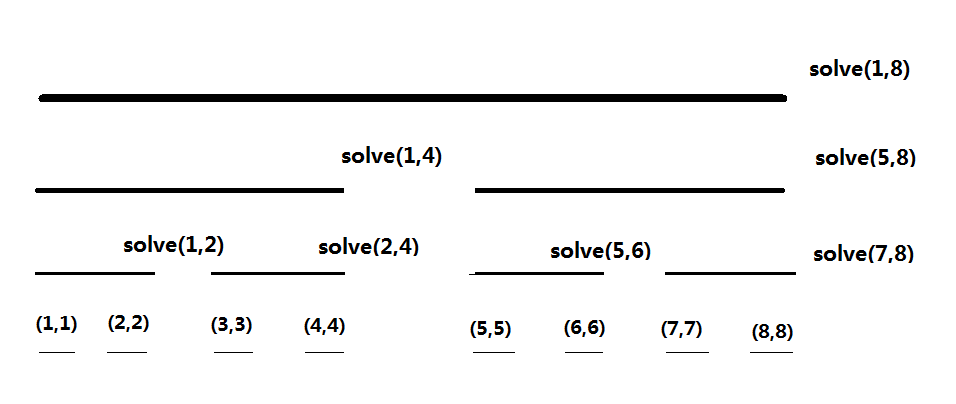
执行刚才的算法流程的话,以 $8$ 这个点为例,它的 DP 值是在 `solve(1,8)`、`solve(5,8)`、`solve(7,8)` 这 3 个函数中更新完成的,而三次用来更新它的点分别是 $(1,4)$、$(5,6)$、$(7,7)$ 这三个不相交的区间;又以 $5$ 这个点为例,它的 DP 值是在 `solve(1,4)` 函数中解决的,更新它的区间是 $(1,4)$。仔细观察就会发现,一个 $i$ 点的 DP 值被更新了 $\log$ 次,而且,更新它的区间刚好是 $(1,i)$ 在线段树上被拆分出来的 $\log$ 个区间。因此,我们的确保证了所有合法的 $j$ 都更新过点 $i$,满足第 2 个条件。
接着分析我们算法的执行流程:
1. 第一个结束的函数是 `solve(1,1)`。此时我们发现 $dp_{1}$ 的值已经计算完毕了;
2. 第一个执行转移过程的函数是 `solve(1,2)`。此时我们发现 $dp_{2}$ 的值已经被转移好了;
3. 第二个结束的函数是 `solve(2,2)`。此时我们发现 $dp_{2}$ 的值已经计算完毕了;
4. 接下来 `solve(1,2)` 结束,$(1,2)$ 这段区间的 $dp$ 值均被计算好;
5. 下一个执行转移流程的函数是 `solve(1,4)`。这次转移结束之后我们发现 $dp_{3}$ 的值已经被转移好了;
6. 接下来结束的函数是 `solve(3,3)`。我们会发现 $dp_{3}$ 的 dp 值被计算好了;
7. 接下来执行的转移是 `solve(2,4)`。此时 $dp_{4}$ 在 `solve(1,4)` 中被 $(1,2)$ 转移了一次,这次又被 $(3,3)$ 转移了,因此 $dp_{4}$ 的值也被转移好了;
8. `solve(4,4)` 结束,$dp_{4}$ 的值计算完毕;
9. `solve(3,4)` 结束,$(3,4)$ 的值计算完毕;
10. `solve(1,4)` 结束,$(1,4)$ 的值计算完毕。
11. ……
通过模拟函数流程,我们发现一件事:每次 `solve(l,r)` 结束的时候,$(l,r)$ 区间的 DP 值会被全部计算好。由于我们每一次执行转移函数的时候,`solve(l,mid)` 已经结束,因此我们每一次执行的转移过程都是合法的,满足第 1 个条件。
在刚才的过程我们发现,如果将 CDQ 分治的递归树看成一颗线段树,那么 CDQ 分治就是这个线段树的 **中序遍历函数**,因此我们相当于按顺序处理了所有的 DP 值,只是转移顺序被拆开了而已,所以算法是正确的。
### 例题
???+ note "[SDOI2011 拦截导弹](https://www.luogu.com.cn/problem/P2487)"
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度、并且能够拦截任意速度的导弹,但是以后每一发炮弹都不能高于前一发的高度,其拦截的导弹的飞行速度也不能大于前一发。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
在不能拦截所有的导弹的情况下,我们当然要选择使国家损失最小、也就是拦截导弹的数量最多的方案。但是拦截导弹数量的最多的方案有可能有多个,如果有多个最优方案,那么我们会随机选取一个作为最终的拦截导弹行动蓝图。
我方间谍已经获取了所有敌军导弹的高度和速度,你的任务是计算出在执行上述决策时,每枚导弹被拦截掉的概率。
??? 参考代码
```cpp
--8<-- "docs/misc/code/cdq-divide/cdq-divide_3.cpp"
// 一道二维最长上升子序列的题
// 为了确定某一个元素是否在最长上升子序列中可以正反跑两遍 CDQ
#include <algorithm>
#include <cstdio>
using namespace std;
typedef double db;
const int N = 1e6 + 10;
struct data_ {
int h;
int v;
int p;
int ma;
db ca;
} a[2][N];
int n;
bool tr;
// 底下是重写比较
bool cmp1(const data_& a, const data_& b) {
if (tr)
return a.h > b.h;
else
return a.h < b.h;
}
bool cmp2(const data_& a, const data_& b) {
if (tr)
return a.v > b.v;
else
return a.v < b.v;
}
bool cmp3(const data_& a, const data_& b) {
if (tr)
return a.p < b.p;
else
return a.p > b.p;
}
bool cmp4(const data_& a, const data_& b) { return a.v == b.v; }
struct treearray {
int ma[2 * N];
db ca[2 * N];
void c(int x, int t, db c) {
for (; x <= n; x += x & (-x)) {
if (ma[x] == t) {
ca[x] += c;
} else if (ma[x] < t) {
ca[x] = c;
ma[x] = t;
}
}
}
void d(int x) {
for (; x <= n; x += x & (-x)) {
ma[x] = 0;
ca[x] = 0;
}
}
void q(int x, int& m, db& c) {
for (; x > 0; x -= x & (-x)) {
if (ma[x] == m) {
c += ca[x];
} else if (m < ma[x]) {
c = ca[x];
m = ma[x];
}
}
}
} ta;
int rk[2][N];
void solve(int l, int r, int t) { // 递归跑
if (r - l == 1) {
return;
}
int mid = (l + r) / 2;
solve(l, mid, t);
sort(a[t] + mid + 1, a[t] + r + 1, cmp1);
int p = l + 1;
for (int i = mid + 1; i <= r; i++) {
for (; (cmp1(a[t][p], a[t][i]) || a[t][p].h == a[t][i].h) && p <= mid;
p++) {
ta.c(a[t][p].v, a[t][p].ma, a[t][p].ca);
}
db c = 0;
int m = 0;
ta.q(a[t][i].v, m, c);
if (a[t][i].ma < m + 1) {
a[t][i].ma = m + 1;
a[t][i].ca = c;
} else if (a[t][i].ma == m + 1) {
a[t][i].ca += c;
}
}
for (int i = l + 1; i <= mid; i++) {
ta.d(a[t][i].v);
}
sort(a[t] + mid, a[t] + r + 1, cmp3);
solve(mid, r, t);
sort(a[t] + l + 1, a[t] + r + 1, cmp1);
}
void ih(int t) {
sort(a[t] + 1, a[t] + n + 1, cmp2);
rk[t][1] = 1;
for (int i = 2; i <= n; i++) {
rk[t][i] = (cmp4(a[t][i], a[t][i - 1])) ? rk[t][i - 1] : i;
}
for (int i = 1; i <= n; i++) {
a[t][i].v = rk[t][i];
}
sort(a[t] + 1, a[t] + n + 1, cmp3);
for (int i = 1; i <= n; i++) {
a[t][i].ma = 1;
a[t][i].ca = 1;
}
}
int len;
db ans;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &a[0][i].h, &a[0][i].v);
a[0][i].p = i;
a[1][i].h = a[0][i].h;
a[1][i].v = a[0][i].v;
a[1][i].p = i;
}
ih(0);
solve(0, n, 0);
tr = 1;
ih(1);
solve(0, n, 1);
tr = 1;
sort(a[0] + 1, a[0] + n + 1, cmp3);
sort(a[1] + 1, a[1] + n + 1, cmp3);
for (int i = 1; i <= n; i++) {
len = max(len, a[0][i].ma);
}
printf("%d\n", len);
for (int i = 1; i <= n; i++) {
if (a[0][i].ma == len) {
ans += a[0][i].ca;
}
}
for (int i = 1; i <= n; i++) {
if (a[0][i].ma + a[1][i].ma - 1 == len) {
printf("%.5lf ", (a[0][i].ca * a[1][i].ca) / ans);
} else {
printf("0.00000 ");
}
}
return 0;
}
```
## 将动态问题转化为静态问题
前两种情况使用 CDQ 分治的目的是将序列折半之后递归处理点对间的关系,来获得良好的复杂度。不过在本节中,折半的不是一般的序列,而是时间序列。
它适用于一些「需要支持做 xxx 修改然后做 xxx 询问」的数据结构题。该类题目有两个特点:
- 如果把询问 [离线](offline.md),所有操作会按照时间自然地排成一个序列。
- 每一个修改均与之后的询问操作息息相关。而这样的「修改 - 询问」关系一共会有 $O(n^2)$ 对。
我们可以使用 CDQ 分治对于这个操作序列进行分治,处理修改和询问之间的关系。
与处理点对关系的 CDQ 分治类似,假设正在分治的序列是 $(l,r)$, 我们先递归地处理 $(l,mid)$ 和 $(mid,r)$ 之间的修改 - 询问关系,再处理所有 $l \leq i \leq mid$,$mid+1 \leq j \leq r$ 的修改 - 询问关系,其中 $i$ 是一个修改,$j$ 是一个询问。
注意,如果各个修改之间是 **独立** 的话,我们无需处理 $l \leq i \leq mid$ 和 $mid+1 \leq j \leq r$,以及 `solve(l,mid)` 和 `solve(mid+1,r)` 之间的时序关系(比如普通的加减法问题)。但是如果各个修改之间并不独立(比如说赋值操作),做完这个修改后,序列长什么样可能依赖于之前的序列。此时处理所有跨越 mid 的修改 - 询问关系的步骤就必须放在 `solve(l,mid)` 和 `solve(mid+1,r)` 之间。理由和 CDQ 分治优化 1D/1D 动态规划的原因是一样的:按照中序遍历序进行分治才能保证每一个修改都是严格按照时间顺序执行的。
### 例题
???+ note "矩形加矩形求和"
维护一个二维平面,然后支持在一个矩形区域内加一个数字,每次询问一个矩形区域的和。
??? 解题思路
对于这个问题的静态版本,即「二维平面里有一堆矩形,我们希望询问一个矩形区域的和」,有一个经典做法叫线段树 + 扫描线。具体的做法是先将每个矩形拆成插入和删除两个操作,接着将每个询问拆成两个前缀和相减的形式,最后离线。然而,原题目是动态的,不能直接使用这种做法。
尝试对其使用 CDQ 分治。我们将所有的询问和修改操作全部离线。这些操作形成了一个序列,并且有 $O(N^2)$ 对修改 - 询问的关系。依然使用 CDQ 分治的一般流程,将所有的关系分成三类,在这一层分治过程当中只处理跨越 $mid$ 的修改 - 询问关系,剩下的修改 - 询问关系通过递归的的方式来解决。
我们发现,所有的修改在询问之前就已完成。这时,原问题等价于「平面上有静态的一堆矩形,不停地询问一个矩形区域的和」。
使用一个扫描线在 $O(n\log n)$ 的时间内处理好所有跨越 $mid$ 的修改 - 询问关系,剩下的事情就是递归地分治左右两侧的修改 - 询问关系了。
在这样实现的 CDQ 分治中,同一个询问被处理了 $O(\log n)$ 次。不过没有关系,因为每次贡献这个询问的修改是互不相交的。全套流程的时间复杂度为 $T(n)=T(\lfloor \frac{n}{2} \rfloor)+T(\lceil \frac{n}{2} \rceil)+ O(n\log n)=O(n\log^2n)$。
观察上述的算法流程,我们发现一开始我们只能解决静态的矩形加矩形求和问题,但只是简单地使用 CDQ 分治后,我们就可以离线地解决一个动态的矩形加矩形求和问题了。将动态问题转化为静态问题的精髓就在于 CDQ 分治每次仅仅处理跨越某一个点的修改和询问关系,这样的话我们就只需要考虑「所有询问都在修改之后」这个简单的问题了。也正是因为这一点,CDQ 分治被称为「动态问题转化为静态问题的工具」。
***
???+ note "[\[Ynoi2016\] 镜中的昆虫](https://www.luogu.com.cn/problem/P4690)"
维护一个长为 $n$ 的序列 $a_i$,有 $m$ 次操作。
1. 将区间 $[l,r]$ 的值修改为 $x$;
2. 询问区间 $[l,r]$ 出现了多少种不同的数,也就是说同一个数出现多次只算一个。
??? 解题思路
一句话题意:区间赋值区间数颜色。
维护一下每个位置左侧第一个同色点的位置,记为 $pre_{i}$,此时区间数颜色就被转化为了一个经典的二维数点问题。
通过将连续的一段颜色看成一个点的方式,可以证明 $pre$ 的变化量是 $O(n+m)$ 的,即单次操作仅仅引起 $O(1)$ 的 $pre$ 值变化,那么我们可以用 CDQ 分治来解决动态的单点加矩形求和问题。
$pre$ 数组的具体变化可以使用 `std::set` 来进行处理。这个用 set 维护连续的区间的技巧也被称之为 [old driver tree](./odt.md)。
??? 参考代码
```cpp
--8<-- "docs/misc/code/cdq-divide/cdq-divide_4.cpp"
#include <algorithm>
#include <cstdio>
#include <map>
#include <set>
#define SNI set<nod>::iterator
#define SDI set<data>::iterator
using namespace std;
const int N = 1e5 + 10;
int n;
int m;
int pre[N];
int npre[N];
int a[N];
int tp[N];
int lf[N];
int rt[N];
int co[N];
struct modi {
int t;
int pos;
int pre;
int va;
friend bool operator<(modi a, modi b) { return a.pre < b.pre; }
} md[10 * N];
int tp1;
struct qry {
int t;
int l;
int r;
int ans;
friend bool operator<(qry a, qry b) { return a.l < b.l; }
} qr[N];
int tp2;
int cnt;
bool cmp(const qry& a, const qry& b) { return a.t < b.t; }
void modify(int pos, int co) // 修改函数
{
if (npre[pos] == co) return;
md[++tp1] = (modi){++cnt, pos, npre[pos], -1};
md[++tp1] = (modi){++cnt, pos, npre[pos] = co, 1};
}
namespace prew {
int lst[2 * N];
map<int, int> mp; // 提前离散化
void prew() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]), mp[a[i]] = 1;
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", &tp[i], &lf[i], &rt[i]);
if (tp[i] == 1) scanf("%d", &co[i]), mp[co[i]] = 1;
}
map<int, int>::iterator it, it1;
for (it = mp.begin(), it1 = it, ++it1; it1 != mp.end(); ++it, ++it1)
it1->second += it->second;
for (int i = 1; i <= n; i++) a[i] = mp[a[i]];
for (int i = 1; i <= n; i++)
if (tp[i] == 1) co[i] = mp[co[i]];
for (int i = 1; i <= n; i++) pre[i] = lst[a[i]], lst[a[i]] = i;
for (int i = 1; i <= n; i++) npre[i] = pre[i];
}
} // namespace prew
namespace colist {
struct data {
int l;
int r;
int x;
friend bool operator<(data a, data b) { return a.r < b.r; }
};
set<data> s;
struct nod {
int l;
int r;
friend bool operator<(nod a, nod b) { return a.r < b.r; }
};
set<nod> c[2 * N];
set<int> bd;
void split(int mid) { // 将一个节点拆成两个节点
SDI it = s.lower_bound((data){0, mid, 0});
data p = *it;
if (mid == p.r) return;
s.erase(p);
s.insert((data){p.l, mid, p.x});
s.insert((data){mid + 1, p.r, p.x});
c[p.x].erase((nod){p.l, p.r});
c[p.x].insert((nod){p.l, mid});
c[p.x].insert((nod){mid + 1, p.r});
}
void del(set<data>::iterator it) { // 删除一个迭代器
bd.insert(it->l);
SNI it1, it2;
it1 = it2 = c[it->x].find((nod){it->l, it->r});
++it2;
if (it2 != c[it->x].end()) bd.insert(it2->l);
c[it->x].erase(it1);
s.erase(it);
}
void ins(data p) { // 插入一个节点
s.insert(p);
SNI it = c[p.x].insert((nod){p.l, p.r}).first;
++it;
if (it != c[p.x].end()) {
bd.insert(it->l);
}
}
void stv(int l, int r, int x) { // 区间赋值
if (l != 1) split(l - 1);
split(r);
int p = l; // split两下之后删掉所有区间
while (p != r + 1) {
SDI it = s.lower_bound((data){0, p, 0});
p = it->r + 1;
del(it);
}
ins((data){l, r, x}); // 扫一遍set处理所有变化的pre值
for (set<int>::iterator it = bd.begin(); it != bd.end(); ++it) {
SDI it1 = s.lower_bound((data){0, *it, 0});
if (*it != it1->l)
modify(*it, *it - 1);
else {
SNI it2 = c[it1->x].lower_bound((nod){0, *it});
if (it2 != c[it1->x].begin())
--it2, modify(*it, it2->r);
else
modify(*it, 0);
}
}
bd.clear();
}
void ih() {
int nc = a[1];
int ccnt = 1; // 将连续的一段插入到set中
for (int i = 2; i <= n; i++)
if (nc != a[i]) {
s.insert((data){i - ccnt, i - 1, nc}),
c[nc].insert((nod){i - ccnt, i - 1});
nc = a[i];
ccnt = 1;
} else {
ccnt++;
}
s.insert((data){n - ccnt + 1, n, a[n]}),
c[a[n]].insert((nod){n - ccnt + 1, n});
}
} // namespace colist
namespace CDQ {
struct treearray // 树状数组
{
int ta[N];
void c(int x, int t) {
for (; x <= n; x += x & (-x)) ta[x] += t;
}
void d(int x) {
for (; x <= n; x += x & (-x)) ta[x] = 0;
}
int q(int x) {
int r = 0;
for (; x; x -= x & (-x)) r += ta[x];
return r;
}
void clear() {
for (int i = 1; i <= n; i++) ta[i] = 0;
}
} ta;
int srt[N];
bool cmp1(const int& a, const int& b) { return pre[a] < pre[b]; }
void solve(int l1, int r1, int l2, int r2, int L, int R) { // CDQ
if (l1 == r1 || l2 == r2) return;
int mid = (L + R) / 2;
int mid1 = l1;
while (mid1 != r1 && md[mid1 + 1].t <= mid) mid1++;
int mid2 = l2;
while (mid2 != r2 && qr[mid2 + 1].t <= mid) mid2++;
solve(l1, mid1, l2, mid2, L, mid);
solve(mid1, r1, mid2, r2, mid, R);
if (l1 != mid1 && mid2 != r2) {
sort(md + l1 + 1, md + mid1 + 1);
sort(qr + mid2 + 1, qr + r2 + 1);
for (int i = mid2 + 1, j = l1 + 1; i <= r2; i++) { // 考虑左侧对右侧贡献
while (j <= mid1 && md[j].pre < qr[i].l) ta.c(md[j].pos, md[j].va), j++;
qr[i].ans += ta.q(qr[i].r) - ta.q(qr[i].l - 1);
}
for (int i = l1 + 1; i <= mid1; i++) ta.d(md[i].pos);
}
}
void mainsolve() {
colist::ih();
for (int i = 1; i <= m; i++)
if (tp[i] == 1)
colist::stv(lf[i], rt[i], co[i]);
else
qr[++tp2] = (qry){++cnt, lf[i], rt[i], 0};
sort(qr + 1, qr + tp2 + 1);
for (int i = 1; i <= n; i++) srt[i] = i;
sort(srt + 1, srt + n + 1, cmp1);
for (int i = 1, j = 1; i <= tp2; i++) { // 初始化一下每个询问的值
while (j <= n && pre[srt[j]] < qr[i].l) ta.c(srt[j], 1), j++;
qr[i].ans += ta.q(qr[i].r) - ta.q(qr[i].l - 1);
}
ta.clear();
sort(qr + 1, qr + tp2 + 1, cmp);
solve(0, tp1, 0, tp2, 0, cnt);
sort(qr + 1, qr + tp2 + 1, cmp);
for (int i = 1; i <= tp2; i++) printf("%d\n", qr[i].ans);
}
} // namespace CDQ
int main() {
prew::prew();
CDQ::mainsolve();
return 0;
}
```
***
???+ note "[\[HNOI2010\] 城市建设](https://www.luogu.com.cn/problem/P3206)"
PS 国是一个拥有诸多城市的大国。国王 Louis 为城市的交通建设可谓绞尽脑汁。Louis 可以在某些城市之间修建道路,在不同的城市之间修建道路需要不同的花费。
Louis 希望建造最少的道路使得国内所有的城市连通。但是由于某些因素,城市之间修建道路需要的花费会随着时间而改变。Louis 会不断得到某道路的修建代价改变的消息。他希望每得到一条消息后能立即知道使城市连通的最小花费总和。Louis 决定求助于你来完成这个任务。
??? 解题思路
一句话题意:给定一张图支持动态的修改边权,要求在每次修改边权之后输出这张图的最小生成树的最小代价和。
事实上,有一个线段树分治套 lct 的做法可以解决这个问题,但是这个实现方式的常数过大,可能需要精妙的卡常技巧才可以通过本题,因此不妨考虑 CDQ 分治来解决这个问题。
和一般的 CDQ 分治解决的问题不同,此时使用 CDQ 分治的时候并没有修改和询问的关系来让我们进行分治,因为无法单独考虑「修改一个边对整张图的最小生成树有什么贡献」。传统的 CDQ 分治思路似乎不是很好使。
通过刚才的例题可以发现,一般的 CDQ 分治和线段树有着特殊的联系:我们在 CDQ 分治的过程中其实隐式地建了一棵线段树出来(因为 CDQ 分治的递归树就是一颗线段树)。通常的 CDQ 是考虑线段树左右儿子之间的联系。而对于这道题,我们需要考虑的是父亲和孩子之间的关系;换句话来讲,我们在 `$solve(l,r)$` 这段区间的时候,如果可以想办法使图的规模变成和区间长度相关的一个变量的话,就可以解决这个问题了。
那么具体来讲如何设计算法呢?
假设我们正在构造 $(l,r)$ 这段区间的最小生成树边集,并且我们已知它父亲最小生成树的边集。我们将在 $(l,r)$ 这段区间中发生变化的边分别赋与 $+ \infty$ 和 $-\infty$ 的边权,并各跑一边 kruskal,求出在最小生成树里的那些边。
对于一条边来讲:
- 如果最小生成树里所有被修改的边权都被赋成了 $+\infty$,而它未出现在树中,则证明它不可能出现在 $(l,r)$ 这些询问的最小生成树当中。所以我们仅仅在 $(l,r)$ 的边集中加入最小生成树的树边。
- 如果最小生成树里所有被修改的边权都被赋成了 $-\infty$,而它未出现在树中,则证明它一定会出现 $(l,r)$ 这段的区间的最小生成树当中。这样的话我们就可以使用并查集将这些边对应的点缩起来,并且将答案加上这些边的边权。
这样我们就将 $(l,r)$ 这段区间的边集构造出来了。用这些边求出来的最小生成树和直接求原图的最小生成树等价。
那么为什么我们的复杂度是对的呢?
首先,修改过的边一定会加进我们的边集,这些边的数目是 $O(len)$ 级别的。
接下来我们需要证明边集当中不会有过多的未被修改的边。我们只会加入所有边权取 $+\infty$ 最小生成树的树边,因此我们加入的边数目不会超过当前图的点数。
现在我们只需证明每递归一层图的点数是 $O(len)$ 级别的,就可以说明图的边数是 $O(len)$ 级别的了。
证明点数是 $O(len)$ 几倍就变得十分简单了。我们每次向下递归的时侯缩掉的边是在 $-\infty$ 生成树中出现的未被修改边,反过来想就是,我们割掉了出现在 $-\infty$ 生成树当中的所有的被修改边。显然我们最多割掉 $len$ 条边,整张图最多分裂成 $O(len)$ 个连通块,这样的话新图点数就是 $O(len)$ 级别的了。所以我们就证明了每次我们用来跑 kruskal 的图都是 $O(len)$ 级别的了,从而每一层的时间复杂度都是 $O(n\log n)$ 了。
时间复杂度是 $T(n)=T(\lfloor \frac{n}{2} \rfloor)+T(\lceil \frac{n}{2} \rceil)+ O(n\log n)=O(n\log^2n)$。
代码实现上可能会有一些难度。需要注意的是并查集不能使用路径压缩,否则就不支持回退操作了。执行缩点操作的时候也没有必要真的执行,而是每一层的 kruskal 都在上一层的并查集里直接做就可以了。
??? 示例代码
```cpp
--8<-- "docs/misc/code/cdq-divide/cdq-divide_5.cpp"
#include <algorithm>
#include <cstdio>
#include <stack>
#include <vector>
using namespace std;
typedef long long ll;
int n;
int m;
int ask;
struct bcj {
int fa[20010];
int size[20010];
struct opt {
int u;
int v;
};
stack<opt> st;
void ih() {
for (int i = 1; i <= n; i++) fa[i] = i, size[i] = 1;
}
int f(int x) { return (fa[x] == x) ? x : f(fa[x]); }
void u(int x, int y) { // 带撤回
int u = f(x);
int v = f(y);
if (u == v) return;
if (size[u] < size[v]) swap(u, v);
size[u] += size[v];
fa[v] = u;
opt o;
o.u = u;
o.v = v;
st.push(o);
}
void undo() {
opt o = st.top();
st.pop();
fa[o.v] = o.v;
size[o.u] -= size[o.v];
}
void clear(int tim) {
while (st.size() > tim) {
undo();
}
}
} s, s1;
struct edge // 静态边
{
int u;
int v;
ll val;
int mrk;
friend bool operator<(edge a, edge b) { return a.val < b.val; }
} e[50010];
struct moved {
int u;
int v;
}; // 动态边
struct query {
int num;
ll val;
ll ans;
} q[50010];
bool book[50010]; // 询问
vector<edge> ve[30];
vector<moved> vq;
vector<edge> tr;
ll res[30];
int tim[30];
void pushdown(int dep) // 缩边
{
tr.clear(); // 这里要复制一份,以免无法回撤操作
for (int i = 0; i < ve[dep].size(); i++) {
tr.push_back(ve[dep][i]);
}
sort(tr.begin(), tr.end());
for (int i = 0; i < tr.size(); i++) { // 无用边
if (s1.f(tr[i].u) == s1.f(tr[i].v)) {
tr[i].mrk = -1;
continue;
}
s1.u(tr[i].u, tr[i].v);
}
s1.clear(0);
res[dep + 1] = res[dep];
for (int i = 0; i < vq.size(); i++) {
s1.u(vq[i].u, vq[i].v);
}
vq.clear();
for (int i = 0; i < tr.size(); i++) { // 必须边
if (tr[i].mrk == -1 || s1.f(tr[i].u) == s1.f(tr[i].v)) continue;
tr[i].mrk = 1;
s1.u(tr[i].u, tr[i].v);
s.u(tr[i].u, tr[i].v);
res[dep + 1] += tr[i].val;
}
s1.clear(0);
ve[dep + 1].clear();
for (int i = 0; i < tr.size(); i++) { // 缩边
if (tr[i].mrk != 0) continue;
edge p;
p.u = s.f(tr[i].u);
p.v = s.f(tr[i].v);
if (p.u == p.v) continue;
p.val = tr[i].val;
p.mrk = 0;
ve[dep + 1].push_back(p);
}
return;
}
void solve(int l, int r, int dep) {
tim[dep] = s.st.size();
int mid = (l + r) / 2;
if (r - l == 1) { // 终止条件
edge p;
p.u = s.f(e[q[r].num].u);
p.v = s.f(e[q[r].num].v);
p.val = q[r].val;
e[q[r].num].val = q[r].val;
p.mrk = 0;
ve[dep].push_back(p);
pushdown(dep);
q[r].ans = res[dep + 1];
s.clear(tim[dep - 1]);
return;
}
for (int i = l + 1; i <= mid; i++) {
book[q[i].num] = true;
}
for (int i = mid + 1; i <= r; i++) { // 动转静
if (book[q[i].num]) continue;
edge p;
p.u = s.f(e[q[i].num].u);
p.v = s.f(e[q[i].num].v);
p.val = e[q[i].num].val;
p.mrk = 0;
ve[dep].push_back(p);
}
for (int i = l + 1; i <= mid; i++) { // 询问转动态
moved p;
p.u = s.f(e[q[i].num].u);
p.v = s.f(e[q[i].num].v);
vq.push_back(p);
}
pushdown(dep); // 下面的是回撤
for (int i = mid + 1; i <= r; i++) {
if (book[q[i].num]) continue;
ve[dep].pop_back();
}
for (int i = l + 1; i <= mid; i++) {
book[q[i].num] = false;
}
solve(l, mid, dep + 1);
for (int i = 0; i < ve[dep].size(); i++) {
ve[dep][i].mrk = 0;
}
for (int i = mid + 1; i <= r; i++) {
book[q[i].num] = true;
}
for (int i = l + 1; i <= mid; i++) { // 动转静
if (book[q[i].num]) continue;
edge p;
p.u = s.f(e[q[i].num].u);
p.v = s.f(e[q[i].num].v);
p.val = e[q[i].num].val;
p.mrk = 0;
ve[dep].push_back(p);
}
for (int i = mid + 1; i <= r; i++) { // 询问转动
book[q[i].num] = false;
moved p;
p.u = s.f(e[q[i].num].u);
p.v = s.f(e[q[i].num].v);
vq.push_back(p);
}
pushdown(dep);
solve(mid, r, dep + 1);
s.clear(tim[dep - 1]);
return; // 时间倒流至上一层
}
int main() {
scanf("%d%d%d", &n, &m, &ask);
s.ih();
s1.ih();
for (int i = 1; i <= m; i++) {
scanf("%d%d%lld", &e[i].u, &e[i].v, &e[i].val);
}
for (int i = 1; i <= ask; i++) {
scanf("%d%lld", &q[i].num, &q[i].val);
}
for (int i = 1; i <= ask; i++) { // 初始动态边
book[q[i].num] = true;
moved p;
p.u = e[q[i].num].u;
p.v = e[q[i].num].v;
vq.push_back(p);
}
for (int i = 1; i <= m; i++) {
if (book[i]) continue;
ve[1].push_back(e[i]);
} // 初始静态
for (int i = 1; i <= ask; i++) {
book[q[i].num] = false;
}
solve(0, ask, 1);
for (int i = 1; i <= ask; i++) {
printf("%lld\n", q[i].ans);
}
return 0;
}
```
## 参考资料与注释
[^ref1]: [从《Cash》谈一类分治算法的应用](https://www.cs.princeton.edu/~danqic/papers/divide-and-conquer.pdf)
---
## 引入
在信息学竞赛中,有一部分题目可以使用二分的办法来解决。但是当这种题目有多次询问且我们每次查询都直接二分可能导致 TLE 时,就会用到整体二分。整体二分的主体思路就是把多个查询一起解决。(所以这是一个离线算法)
> 可以使用整体二分解决的题目需要满足以下性质:
>
> 1. 询问的答案具有可二分性
>
> 2. **修改对判定答案的贡献互相独立**,修改之间互不影响效果
>
> 3. 修改如果对判定答案有贡献,则贡献为一确定的与判定标准无关的值
>
> 4. 贡献满足交换律,结合律,具有可加性
>
> 5. 题目允许使用离线算法
>
> ——许昊然《浅谈数据结构题几个非经典解法》
## 解释
记 $[l,r]$ 为答案的值域,$[L,R]$ 为答案的定义域。(也就是说求答案时仅考虑下标在区间 $[L,R]$ 内的操作和询问,这其中询问的答案在 $[l,r]$ 内)
- 我们首先把所有操作 **按时间顺序** 存入数组中,然后开始分治。
- 在每一层分治中,利用数据结构(常见的是树状数组)统计当前查询的答案和 $mid$ 之间的关系。
- 根据查询出来的答案和 $mid$ 间的关系(小于等于 $mid$ 和大于 $mid$)将当前处理的操作序列分为 $q1$ 和 $q2$ 两份,并分别递归处理。
- 当 $l=r$ 时,找到答案,记录答案并返回即可。
需要注意的是,在整体二分过程中,若当前处理的值域为 $[l,r]$,则此时最终答案范围不在 $[l,r]$ 的询问会在其他时候处理。
## 过程
注:
1. 为可读性,文中代码或未采用实际竞赛中的常见写法。
2. 若觉得某段代码有难以理解之处,请先参考之前题目的解释,
因为节省篇幅解释过的内容不再赘述。
从普通二分说起:
### 查询全局第 k 小
> **题 1** 在一个数列中查询第 $k$ 小的数。
当然可以直接排序。如果用二分法呢?可以用数据结构记录每个大小范围内有多少个数,然后用二分法猜测,利用数据结构检验。
> **题 2** 在一个数列中多次查询第 $k$ 小的数。
可以对于每个询问进行一次二分;但是,也可以把所有的询问放在一起二分。
先考虑二分的本质:假设要猜一个 $[l,r]$ 之间的数,猜测之后会知道是猜大了,猜小了还是刚好。当然可以从 $l$ 枚举到 $r$,但更优秀的方法是二分:猜测答案是 $m = \lfloor\frac{l + r}{2}\rfloor$,然后去验证 $m$ 的正确性,再调整边界。这样做每次询问的复杂度为 $O(\log n)$,若询问次数为 $q$,则时间复杂度为 $O(q\log n)$。
回过头来,对于当前的所有询问,可以去猜测所有询问的答案都是 $mid$,然后去依次验证每个询问的答案应该是小于等于 $mid$ 的还是大于 $mid$ 的,并将询问分为两个部分(不大于/大于),对于每个部分继续二分。注意:如果一个询问的答案是大于 $mid$ 的,则在将其划至右侧前需更新它的 $k$,即,如果当前数列中小于等于 $mid$ 的数有 $t$ 个,则将询问划分后实际是在右区间询问第 $k - t$ 小数。如果一个部分的 $l = r$ 了,则结束这个部分的二分。利用线段树的相关知识,我们每次将整个答案可能在的区间 $[1,maxans]$ 划分成了若干个部分,这样的划分共进行了 $O(\log maxans)$ 次,一次划分会将整个操作序列操作一次。若对整个序列进行操作,并支持对应的查询的时间复杂度为 $O(T)$,则整体二分的时间复杂度为 $O(T\log n)$。
试试完成以下代码:
```cpp
struct Query {
int id, k; // 这个询问的编号, 这个询问的k
};
int ans[N]; // ans[i] 表示编号为i的询问的答案
int check(int x); // 返回原数列中小于等于x的数的个数
void solve(int l, int r, vector<Query> q)
// 请补全这个函数
{
int m = (l + r) / 2;
vector<Query> q1, q2; // 将被划到左侧的询问和右侧的询问
if (l == r) {
// ...
return;
}
// ...
solve(l, m, q1), solve(m + 1, r, q2);
return;
}
```
参考代码如下
???+ note "实现"
```cpp
void solve(int l, int r, vector<Query> q) {
int m = (l + r) / 2;
if (l == r) {
for (unsigned i = 0; i < q.size(); i++) ans[q[i].id] = l;
return;
}
vector<int> q1, q2;
for (unsigned i = 0; i < q.size(); i++)
if (q[i].k <= check(m))
q1.push_back(q[i]);
else
q[i].k -= check(m), q2.push_back(q[i]);
solve(l, m, q1), solve(m + 1, r, q2);
return;
}
```
### 查询区间第 k 小
> **题 3** 在一个数列中多次查询区间第 $k$ 小的数。
涉及到给定区间的查询,再按之前的方法进行二分就会导致 `check` 函数的时间复杂度爆炸。仍然考虑询问与值域中点 $m$ 的关系:若询问区间内小于等于 $m$ 的数有 $t$ 个,询问的是区间内的 $k$ 小数,则当 $k \leq t$ 时,答案应小于等于 $m$;否则,答案应大于 $m$。(注意边界问题)此处需记录一个区间小于等于指定数的数的数量,即单点加,求区间和,可用树状数组快速处理。为提高效率,只对数列中值在值域区间 $[l,r]$ 的数进行统计,即,在进一步递归之前,不仅将询问划分,将当前处理的数按值域范围划为两半。
参考代码(关键部分)
???+ note "实现"
```cpp
struct Num {
int p, x;
}; // 位于数列中第 p 项的数的值为 x
struct Query {
int l, r, k, id;
}; // 一个编号为 id, 询问 [l,r] 中第 k 小数的询问
int ans[N];
void add(int p, int x); // 树状数组, 在 p 位置加上 x
int query(int p); // 树状数组, 求 [1,p] 的和
void clear(); // 树状数组, 清空
void solve(int l, int r, vector<Num> a, vector<Query> q)
// a中为给定数列中值在值域区间 [l,r] 中的数
{
int m = (l + r) / 2;
if (l == r) {
for (unsigned i = 0; i < q.size(); i++) ans[q[i].id] = l;
return;
}
vector<Num> a1, a2;
vector<Query> q1, q2;
for (unsigned i = 0; i < a.size(); i++)
if (a[i].x <= m)
a1.push_back(a[i]), add(a[i].p, 1);
else
a2.push_back(a[i]);
for (unsigned i = 0; i < q.size(); i++) {
int t = query(q[i].r) - query(q[i].l - 1);
if (q[i].k <= t)
q1.push_back(q[i]);
else
q[i].k -= t, q2.push_back(q[i]);
}
clear();
solve(l, m, a1, q1), solve(m + 1, r, a2, q2);
return;
}
```
下面提供 [【模板】可持久化线段树 2](https://www.luogu.com.cn/problem/P3834) 一题使用整体二分的,偏向竞赛风格的写法。
???+ note "参考代码"
```cpp
--8<-- "docs/misc/code/parallel-binsearch/parallel-binsearch_1.cpp"
#include <bits/stdc++.h>
using namespace std;
const int N = 200020;
const int INF = 1e9;
int n, m;
int ans[N];
// BIT begin
int t[N];
int a[N];
int sum(int p) {
int ans = 0;
while (p) {
ans += t[p];
p -= p & (-p);
}
return ans;
}
void add(int p, int x) {
while (p <= n) {
t[p] += x;
p += p & (-p);
}
}
// BIT end
int tot = 0;
struct Query {
int l, r, k, id, type; // set values to -1 when they are not used!
} q[N * 2], q1[N * 2], q2[N * 2];
void solve(int l, int r, int ql, int qr) {
if (ql > qr) return;
if (l == r) {
for (int i = ql; i <= qr; i++)
if (q[i].type == 2) ans[q[i].id] = l;
return;
}
int mid = (l + r) / 2, cnt1 = 0, cnt2 = 0;
for (int i = ql; i <= qr; i++) {
if (q[i].type == 1) {
if (q[i].l <= mid) {
add(q[i].id, 1);
q1[++cnt1] = q[i];
} else
q2[++cnt2] = q[i];
} else {
int x = sum(q[i].r) - sum(q[i].l - 1);
if (q[i].k <= x)
q1[++cnt1] = q[i];
else {
q[i].k -= x;
q2[++cnt2] = q[i];
}
}
}
// rollback changes
for (int i = 1; i <= cnt1; i++)
if (q1[i].type == 1) add(q1[i].id, -1);
// move them to the main array
for (int i = 1; i <= cnt1; i++) q[i + ql - 1] = q1[i];
for (int i = 1; i <= cnt2; i++) q[i + cnt1 + ql - 1] = q2[i];
solve(l, mid, ql, cnt1 + ql - 1);
solve(mid + 1, r, cnt1 + ql, qr);
}
pair<int, int> b[N];
int toRaw[N];
int main() {
scanf("%d%d", &n, &m);
// read and discrete input data
for (int i = 1; i <= n; i++) {
int x;
scanf("%d", &x);
b[i].first = x;
b[i].second = i;
}
sort(b + 1, b + n + 1);
int cnt = 0;
for (int i = 1; i <= n; i++) {
if (b[i].first != b[i - 1].first) cnt++;
a[b[i].second] = cnt;
toRaw[cnt] = b[i].first;
}
for (int i = 1; i <= n; i++) {
q[++tot] = {a[i], -1, -1, i, 1};
}
for (int i = 1; i <= m; i++) {
int l, r, k;
scanf("%d%d%d", &l, &r, &k);
q[++tot] = {l, r, k, i, 2};
}
solve(0, cnt + 1, 1, tot);
for (int i = 1; i <= m; i++) printf("%d\n", toRaw[ans[i]]);
}```
### 带修区间第 k 小
> **题 4** [Dynamic Rankings](http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=2112) 给定一个数列,要支持单点修改,区间查第 $k$ 小。
修改操作可以直接理解为从原数列中删去一个数再添加一个数,为方便起见,将询问和修改统称为「操作」。因后面的操作会依附于之前的操作,不能如题 3 一样将统计和处理询问分开,故可将所有操作存于一个数组,用标识区分类型,依次处理每个操作。为便于处理树状数组,修改操作可分拆为擦除操作和插入操作。
**优化**
1. 注意到每次对于操作进行分类时,只会更改操作顺序,故可直接在原数组上操作。具体实现,在二分时将记录操作的 $q, a$ 数组换为一个大的全局数组,二分时记录信息变为 $L, R$,即当前处理的操作是全局数组上的哪个区间。利用临时数组记录当前的分类情况,进一步递归前将临时数组信息写回原数组。
2. 树状数组每次清空会导致时间复杂度爆炸,可采用每次使用树状数组时记录当前修改位置(这已由 1 中提到的临时数组实现),本次操作结束后在原位置加 $-1$ 的方法快速清零。
3. 一开始对于数列的初始化操作可简化为插入操作。
参考代码(关键部分)
???+ note "实现"
```cpp
struct Opt {
int x, y, k, type, id;
// 对于询问, type = 1, x, y 表示区间左右边界, k 表示询问第 k 小
// 对于修改, type = 0, x 表示修改位置, y 表示修改后的值,
// k 表示当前操作是插入(1)还是擦除(-1), 更新树状数组时使用.
// id 记录每个操作原先的编号, 因二分过程中操作顺序会被打散
};
Opt q[N], q1[N], q2[N];
// q 为所有操作,
// 二分过程中, 分到左边的操作存到 q1 中, 分到右边的操作存到 q2 中.
int ans[N];
void add(int p, int x);
int query(int p); // 树状数组函数, 含义见题3
void solve(int l, int r, int L, int R)
// 当前的值域范围为 [l,r], 处理的操作的区间为 [L,R]
{
if (l > r || L > R) return;
int cnt1 = 0, cnt2 = 0, m = (l + r) / 2;
// cnt1, cnt2 分别为分到左边, 分到右边的操作数
if (l == r) {
for (int i = L; i <= R; i++)
if (q[i].type == 1) ans[q[i].id] = l;
return;
}
for (int i = L; i <= R; i++)
if (q[i].type == 1) { // 是询问: 进行分类
int t = query(q[i].y) - query(q[i].x - 1);
if (q[i].k <= t)
q1[++cnt1] = q[i];
else
q[i].k -= t, q2[++cnt2] = q[i];
} else
// 是修改: 更新树状数组 & 分类
if (q[i].y <= m)
add(q[i].x, q[i].k), q1[++cnt1] = q[i];
else
q2[++cnt2] = q[i];
for (int i = 1; i <= cnt1; i++)
if (q1[i].type == 0) add(q1[i].x, -q1[i].k); // 清空树状数组
for (int i = 1; i <= cnt1; i++) q[L + i - 1] = q1[i];
for (int i = 1; i <= cnt2; i++)
q[L + cnt1 + i - 1] = q2[i]; // 将临时数组中的元素合并回原数组
solve(l, m, L, L + cnt1 - 1), solve(m + 1, r, L + cnt1, R);
return;
}
```
### 针对静态序列的优化
> **题 5** [【模板】可持久化线段树 2](https://www.luogu.com.cn/problem/P3834) 给定一个序列,区间查询第 $k$ 小。
树套树和整体二分实现带修区间第 $k$ 小问题的复杂度都为 $O(n \log^2 n)$,但静态区间第 $k$ 小问题可以使用可持久化线段树在 $O(n \log n)$ 时间复杂度内解决,而几乎所有整体二分实现的静态区间第 $k$ 小问题代码时间复杂度都是 $O(n \log^2 n)$,面对大数据范围时存在 TLE 的风险。(这里默认值域与序列长度同阶,值域与序列长不同阶的情况可以通过离散化转化为同阶情况)
**优化**
1. 对于每一轮划分,如果当前数列中小于等于 $mid$ 的数有 $t$ 个,则将询问划分后实际是在右区间询问第 $k - t$ 小数,因此对划分到右区间的询问做出了修改。如果答案的原始值域为 $[L,R]$,某次划分的答案值域为 $[l,r]$,那么对于参与此次划分的询问,$[L,l)$ 中所有数值对它们的影响已经在之前被消除了。
2. 由于需要使每轮划分都仅和当前答案值域 $[l,r]$ 有关,树状数组需要多次载入和清空。
如果划分不仅仅和当前答案值域有关呢?
由此可以得到一个与全局序列有关的优化方法:维护一个指针 $pos$ 追踪每轮划分的 $mid$(分治中心),将所有 $\leq pos$ 的元素对应的下标在树状数组中置为 $1$,树状数组的其余位置置为 $0$。每次划分之前移动 $pos$ 并更新树状数组。指针 $pos$ 移动的次数与 $n \log n$ 同阶。划分时对每一个询问查询树状数组中对应区间的值,满足则划分至左区间,否则划分至右区间,**不需要对询问做出修改**。
由于要追踪分治中心,需要让 $pos$ 准确地更新树状数组。在整体二分之前将序列按元素大小排序并记录元素对应下标,指针移动时在树状数组中对下标进行相应修改。对于绝大多数 **可以用整体二分解决并且不带修改的问题**,都可以应用此种优化以大幅降低数据结构的使用次数。
由于减少了很多树状数组的载入和清空操作,应用这种优化通常情况下会明显提升整体二分的效率(即使只是常数优化),对于静态区间第 $k$ 小值问题而言效率完全不差于时间复杂度更优的可持久化线段树。值得注意的是,对于静态区间第 $k$ 小值问题也存在时间复杂度 $O(n \log n)$ 的整体二分实现。
参考代码(关键部分)
???+ note "实现"
```cpp
struct Query {
int i, l, r, k;
}; // 第 i 次询问查询区间 [l,r] 的第 k 小值
Query s[200005], t1[200005], t2[200005];
int n, m, cnt, pos, p[200005], ans[200005];
pair<int, int> a[200005];
void add(int x, int y); // 树状数组 位置 x 加 y
int sum(int x); // 树状数组 [1,x] 前缀和
// 当前处理的询问为 [l,r],答案值域为 [ql,qr]
void overall_binary(int l, int r, int ql, int qr) {
if (l > r) return;
if (ql == qr) {
for (int i = l; i <= r; i++) ans[s[i].i] = ql;
return;
}
int cnt1 = 0, cnt2 = 0, mid = (ql + qr) >> 1;
// 追踪分治中心,认为 [1,pos] 的值已经载入树状数组
while (pos <= n - 1 && a[pos + 1].first <= mid)
add(a[pos + 1].second, 1), ++pos;
while (pos >= 1 && a[pos].first > mid) add(a[pos].second, -1), --pos;
for (int i = l; i <= r; i++) {
int now = sum(s[i].r) - sum(s[i].l - 1);
if (s[i].k <= now)
t1[++cnt1] = s[i];
else
t2[++cnt2] = s[i]; // 注意 不应修改询问信息
}
for (int i = 1; i <= cnt1; i++) s[l + i - 1] = t1[i];
for (int i = 1; i <= cnt2; i++) s[l + cnt1 + i - 1] = t2[i];
overall_binary(l, l + cnt1 - 1, ql, mid);
overall_binary(l + cnt1, r, mid + 1, qr);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i].first);
a[i].second = i;
p[++cnt] = a[i].first;
}
sort(a + 1, a + n + 1); // 对序列排序 离散化
sort(p + 1, p + n + 1);
cnt = unique(p + 1, p + n + 1) - p - 1;
for (int i = 1; i <= n; i++)
a[i].first = lower_bound(p + 1, p + cnt + 1, a[i].first) - p;
// 省略读入询问
overall_binary(1, m, 1, cnt);
for (int i = 1; i <= n; i++) printf("%d\n", p[ans[i]]);
return 0;
}
```
### 区间前驱后继
> **题 6** 在一个数列中多次查询 $k$ 在区间中的前驱(严格小于 $k$,且最大的数)或后继(严格大于 $k$,且最小的数),保证存在这样的数。
以前驱为例,使用数据结构解决此种问题的方法一般是先查询区间内有多少严格小于 $k$ 的数(设它们的数量为 $x$),再查询区间第 $x$ 小的数。后继则是查询区间内有多少不大于 $k$ 的数(数量为 $x$),然后查询区间第 $x+1$ 小的数。
考虑使用整体二分解决这个问题:整体二分是一种高效求解区间第 $k$ 小的离线算法,而 [CDQ 分治](https://oi-wiki.org/misc/cdq-divide/) 可以离线高效求解区间内的排名。先跑一遍 CDQ 分治求出排名就可以使用整体二分得到区间内部的前驱和后继了。
此问题还可以用 CDQ 分治套线段树离线一遍解决,但效率远低于跑两遍的 CDQ 分治 + 整体二分。
### 构造单调性序列
> **题 7** [Sequence](https://www.luogu.com.cn/problem/P4597) 给定一个序列,每次操作可以把某个数 $+1$ 或 $−1$。要求把序列变成单调不降的,并且修改后的数列只能出现修改前的数,输出最小操作次数。
此类题目也可以使用动态规划或反悔贪心解决。
在满足操作次数最小化的前提下,一定存在一种方案使得最后序列中的每个数都是序列修改前存在的,这个结论可以使用数学归纳法证明。由于题目并不需要最终序列的信息,问题转化为求出最小操作次数。
由于要求最终的序列单调不降,可以使用整体二分。每轮整体二分判定最终序列区间 $[l,r]$ 的值域,此时答案的值域为 $[ql,qr]$。令 $mid=\lfloor\frac{ql + qr}{2}\rfloor$,每轮二分开始时默认将所有数划分至 $[mid+1,qr]$(要划分到 $[ql,mid]$ 的数设为 $0$ 个),初始代价设为将序列区间 $[l,r]$ 全部置为 $mid+1$ 的操作次数。依次枚举区间 $[l,r]$ 中的数 $i$ 并且计算将 $[l,i]$ 置为 $mid$、将 $[i+1,r]$ 置为 $mid+1$ 的操作次数之和,如果优于之前的操作次数则更新最少操作次数和要划分到 $[ql,mid]$ 的数的个数。
划分时已经保证了最终序列的单调性不被破坏,同时因为每次都取最小操作次数,最终被划分至左区间的数取 $mid$ 一定比取 $mid+1$ 更优,故整体二分得到的序列一定是单调不降且操作次数最小的。计算操作次数输出即可。
参考代码(关键部分)
???+ note "实现"
```cpp
int a[500005], ans[500005]; // a:原序列 ans:构造的序列
void overall_binary(int l, int r, int ql, int qr) {
if (l > r) return;
if (ql == qr) {
for (int i = l; i <= r; i++) ans[i] = ql;
return;
}
int cnt = 0,
mid = ql + ((qr - ql) >> 1); // 默认开始都填 mid+1 全部划分到右区间
long long res = 0ll, sum = 0ll;
for (int i = l; i <= r; i++) sum += abs(a[i] - (mid + 1));
res = sum;
for (int i = l; i <= r;
i++) { // 尝试把 [l,i] 从 mid+1 换成 mid 并且划分到左区间
sum -= abs(a[i] - (mid + 1));
sum += abs(a[i] - mid);
if (sum < res) cnt = i - l + 1, res = sum; // 发现 [l,i] 取 mid 更优,更新
}
overall_binary(l, l + cnt - 1, ql, mid);
overall_binary(l + cnt, r, mid + 1, qr);
}
```
### 参考习题
[「国家集训队」矩阵乘法](https://www.luogu.com.cn/problem/P1527)
[「POI2011 R3 Day2」流星 Meteors](https://loj.ac/p/2169)
[二逼平衡树](https://loj.ac/p/106)
[\[BalticOI 2004\] Sequence 数字序列](https://www.luogu.com.cn/problem/P4331)
## 参考资料
- 许昊然《浅谈数据结构题几个非经典解法》
---
@[toc]
今天要学习的算法是莫队算法基础版本。
# 1. 莫队概述
莫队是一种解决区间查询问题的离线算法。它的思想很简单,本质上就是**通过<font color="red">挪动区间</font>的方式按照<font color="red">某种顺序</font>,<font color="red">离线处理</font>区间查询操作**。
它的时间复杂度是 $\text{O(n}\sqrt{n})$ ,是一种效率不错的算法,可以解决几乎所有的区间查询问题(需要离线),只要对时间复杂度的要求不是那么苛刻。
---
# 2. 挪动区间
假设有这样的一道题:**对于一个数列,每次给出一个区间询问 `[L,R]` ,求它的区间和**。这道题用前缀和很容易做出来,不过我们强制用莫队做。
对于下面的例子,**首先要开一个数组存储数列**。注意,区间从 `1` 开始:
```cpp
0 1 2 3 4 5 6 7 8 9 |index
3 8 1 2 7 4 9 0 6 |val
```
假设我们此时已经知道 `[2,5]` 区间的和是 `18` ,有如下询问:
- 求 `[2,6]` 区间的和:用 `[2,5]` 区间的和,加上第六项的值即可,答案是 `18+4=22` ;
- 求 `[2,4]` 区间的和:用 `[2,5]` 区间的和,减去第五项的值即可,答案为 `18-7=11` ;
- 求 `[3,6]` 区间的和:用 `[2,5]` 区间的和,减去第二项的值,再加上第六项的值就可以求出;
- 其他区间依次类推。
由此,对当前区间 `[L,R]` ,我们分别讨论四种情况:
1. 加上当前区间左边一格 `L - 1` 处的贡献:`Add(--L);`
2. 加上当前区间右边一格 `R + 1` 处的贡献:`Add(++R);`
3. 减去当前区间最左一格 `L` 处的贡献:`Sub(L++);`
4. 减去当前区间最右一格 `R` 处的贡献:`Sub(R--);`
可以看到,我们不只是修改了区间的总贡献,还修改了区间的 `[L, R]` 边界。这样,**所有的区间都可以从当前已知区间的结果扩展出来。**
# 3. 某种顺序和离线处理
仅仅这样是远远不够的,对于一个 `n` 项的数列,假设这样询问 `m` 次:
```cpp
[1,2], [n-1,n], [1,2], [n-1,n] ...
```
无疑,时间复杂度爆炸了,它将变成一个 $\text{O(mn)}$ 的算法。但是对于同样的这些询问,如果是以下的顺序:
```cpp
[1,2], [1,2] ... [n-1,n], [n-1,n] ...
```
时间复杂度瞬间优化到 $\text{O(m+n)}$ ,速度大大提升。可见,**询问顺序对莫队算法的时间复杂度有着很大的影响**。甚至可以说,莫队算法要满足的必要条件就是**必须以接近 $\text{O(1)}$ 的时间移动区间**。如果可以在 $O(1)$ 内从 $[l,r]$ 的答案,移动到 $[l-1,r], [l+1, r], [l, r-1], [l, r+1]$ 这四个与之紧邻的区间并得出答案,就可以考虑使用莫队。
那么怎样排序来解决询问顺序呢?很容易想到使用 $l$ 作为第一个关键字、$r$ 作为第二关键字进行排序,但这样的效果不是很好。为此,我们需要使用**分块**进行优化。具体做法如下:
- 首先分块,块大小就是普通的 $\sqrt{n}$ ;
- 然后对所有的询问进行排序,排序规则如下:对于一个询问 `[L,R]` ,首先按照区间的 `L` 边界所在块的编号从小到大排序;对于处在同一块的,按照 `R` 的大小进行排序;
- 排序后,遍历所有询问,进行区间的移动,得到各个询问的答案记录下来;
- 最后,按照这些询问的原顺序输出答案即可。
看完上面的过程,我们就能够明白,为什么莫队要求离线。
---
# 4. 莫队算法框架
下面给出基础莫队的代码框架:
```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e4 + 5;
int a[maxn]; //记录所有数据的数组
int pos[maxn]; //a数列中的第几项是第几块的
int ans[maxn]; //记录所有询问的答案(按照原来的顺序)
//询问的结构体
struct Q {
int l, r, k; //询问的区间[l,r], 第几个询问
} q[maxn];
//记录某一个由[L,R]规定的闭区间的区间结果
int res = 0;
//挪动区间的函数
void Add(int n) { ... }
void Sub(int n) { ... }
int main() {
//n个数据,m个询问
int n, m;
cin >> n >> m;
//记录数据和分块
int size = sqrt(n); //块的大小
for (int i = 1; i <= n; ++i) {
cin >> a[i];
pos[i] = i / size; //每个数据处于哪一块
}
//记录询问
for (int i = 0; i < m; ++i) {
cin >> q[i].l >> q[i].r;
q[i].k = i; //第几个询问,用来记录询问的原始顺序
}
//所有询问进行排序,同一个块按照r排序,否则按照块顺序排
sort(q, q + m, [](Q x, Q y)
{ return pos[x.l] == pos[y.l] ? x.r < y.r : pos[x.l] < pos[y.l] });
//当前所知的闭区间[l,r]
int l = 1, r = 0;
//遍历所有的询问
for (int i = 0; i < m; ++i) {
while (q[i].l < l) Add(--l);
while (q[i].r > r) Add(++r);
while (q[i].l > l) Sub(l++);
while (q[i].r < r) Sub(r--);
//按照原始顺序记录答案
ans[q[i].k] = res;
}
//输出ans数组作为答案
...
return 0;
}
```
---
# 5. 应用题
基础莫队:[P2709 小B的询问](https://www.luogu.com.cn/problem/P2709)
基础莫队:[P3901 数列找不同](https://www.luogu.com.cn/problem/P3901)
基础莫队:[SPOJ DQUERY - D-query](https://www.spoj.com/problems/DQUERY/)
---
# 6. 常数优化:奇偶化排序
上面的分块排序,就可以有效降低每两次询问间 $l, r$ 移动的距离。但在此之上,我们还可以进行常数优化:**奇偶化排序**。即块号 `pos[l]` 不相等时,按照块号从小到大排序;相等时如果 `pos[l]` 是奇数,则将 `r` 从小到大排序,否则按照 `r` 从大到小排序。为什么它是有效的?
如果按照一般的排序方法,指针会这样移动:在 `l` 处于同一块时,指针 `r` 不断往右移;每当 `l` 跨越一个块时,`r` 都必须从右向左移动很长一段距离:
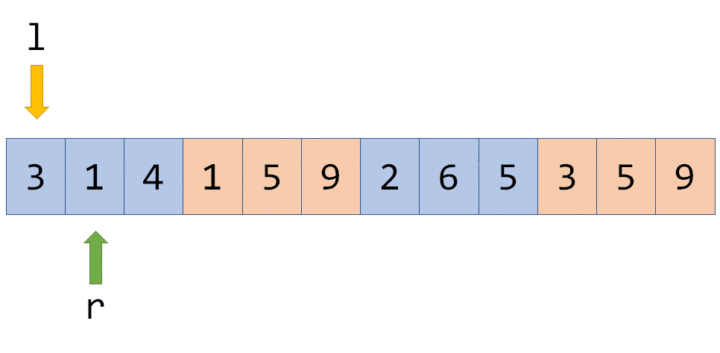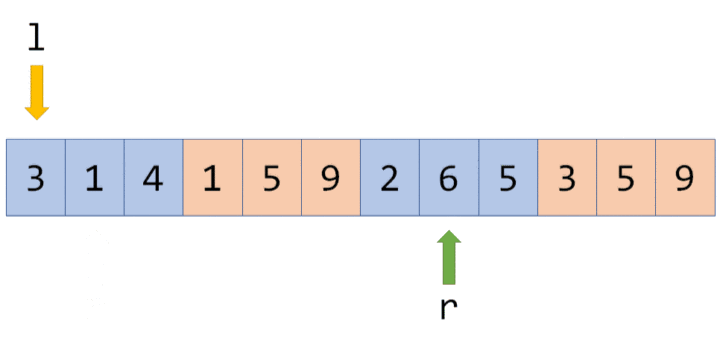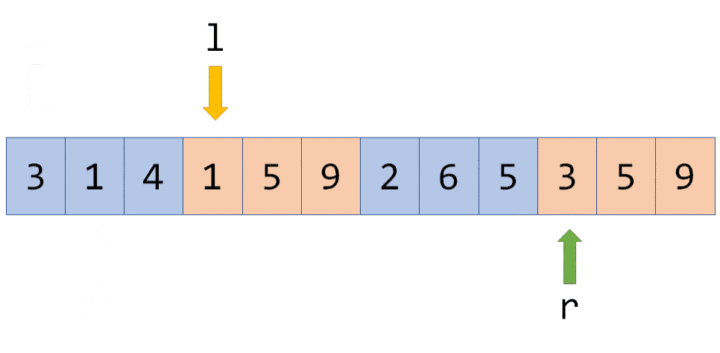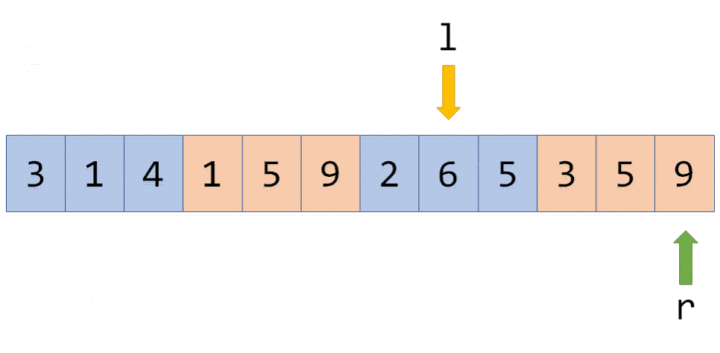
而奇偶化排序后,指针会这样移动:在 `l` 处于奇数块时,指针 `r` 不断往右移,解决所有块内的询问;`l` 跨越到下一块(偶数块)时,`r` 指针不断往左移,在返回的过程中解决按照 `r` 从大到小排序的询问:
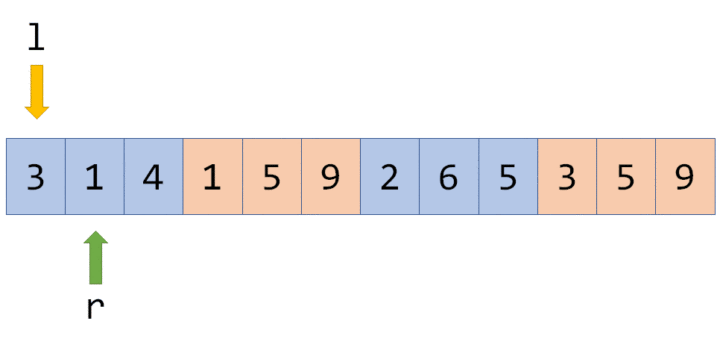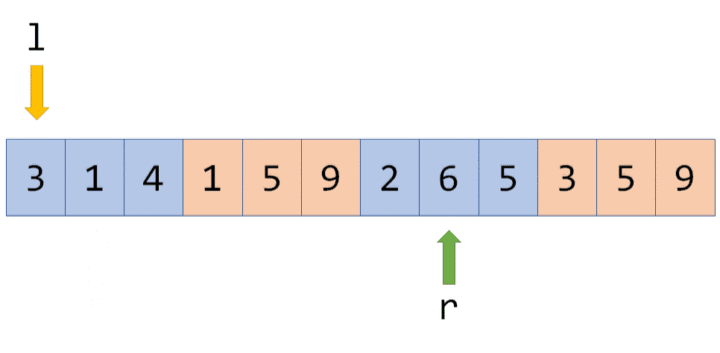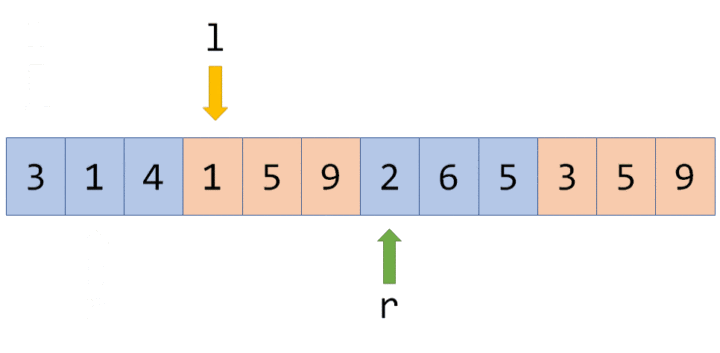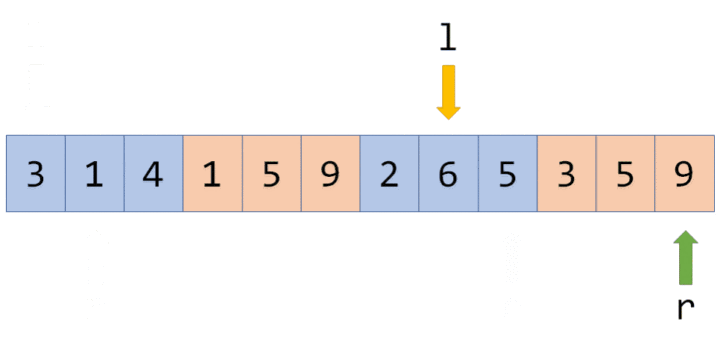
询问的结构体代码如下:
```cpp
const int MAXN = 1e5 + 10;
int sqr = sqrt(n);
struct Q {
int l, r, id;
bool operator<(const Q &b) const { //重载<运算符,奇偶化排序
//只需要知道每个元素归属于哪个块,块大小为sqrt(n),所以直接l/sqrt(n)即可
if (l / sqr != b.l / sqr) return l < b.l;
if (l / sqr & 1) //奇数块
return r < b.r;
return r > b.r;
}
} Q[MAXN];
```
---
author: StudyingFather, Backl1ght, countercurrent-time, Ir1d, greyqz, MicDZ, ouuan
莫队算法是由莫涛提出的算法。在莫涛提出莫队算法之前,莫队算法已经在 Codeforces 的高手圈里小范围流传,但是莫涛是第一个对莫队算法进行详细归纳总结的人。莫涛提出莫队算法时,只分析了普通莫队算法,但是经过 OIer 和 ACMer 的集体智慧改造,莫队有了多种扩展版本。
莫队算法可以解决一类离线区间询问问题,适用性极为广泛。同时将其加以扩展,便能轻松处理树上路径询问以及支持修改操作。
author: StudyingFather, Backl1ght, countercurrent-time, Ir1d, greyqz, MicDZ, ouuan
## 形式
假设 $n=m$,那么对于序列上的区间询问问题,如果从 $[l,r]$ 的答案能够 $O(1)$ 扩展到 $[l-1,r],[l+1,r],[l,r+1],[l,r-1]$(即与 $[l,r]$ 相邻的区间)的答案,那么可以在 $O(n\sqrt{n})$ 的复杂度内求出所有询问的答案。
## 解释
离线后排序,顺序处理每个询问,暴力从上一个区间的答案转移到下一个区间答案(一步一步移动即可)。
## 排序方法
对于区间 $[l,r]$, 以 $l$ 所在块的编号为第一关键字,$r$ 为第二关键字从小到大排序。
## 实现
```cpp
void move(int pos, int sign) {
// update nowAns
}
void solve() {
BLOCK_SIZE = int(ceil(pow(n, 0.5)));
sort(querys, querys + m);
for (int i = 0; i < m; ++i) {
const query &q = querys[i];
while (l > q.l) move(--l, 1);
while (r < q.r) move(r++, 1);
while (l < q.l) move(l++, -1);
while (r > q.r) move(--r, -1);
ans[q.id] = nowAns;
}
}
```
## 复杂度分析
以下的情况在 $n$ 和 $m$ 同阶的前提下讨论。
首先是分块这一步,这一步的时间复杂度是 $O(\sqrt{n}\cdot\sqrt{n}\log\sqrt{n}+n\log n)=O(n\log n)$;
接着就到了莫队算法的精髓了,下面我们用通俗易懂的初中方法来证明它的时间复杂度是 $O(n\sqrt{n})$;
???+ note "证明"
证:令每一块中 $L$ 的最大值为 $\max_1,\max_2,\max_3, \cdots , \max_{\lceil\sqrt{n}\rceil}$。
由第一次排序可知,$\max_1 \le \max_2 \le \cdots \le \max_{\lceil\sqrt{n}\rceil}$。
显然,对于每一块暴力求出第一个询问的时间复杂度为 $O(n)$。
考虑最坏的情况,在每一块中,$R$ 的最大值均为 $n$,每次修改操作均要将 $L$ 由 $\max_{i - 1}$ 修改至 $\max_i$ 或由 $\max_i$ 修改至 $\max_{i - 1}$。
考虑 $R$:因为 $R$ 在块中已经排好序,所以在同一块修改完它的时间复杂度为 $O(n)$。对于所有块就是 $O(n\sqrt{n})$。
重点分析 $L$:因为每一次改变的时间复杂度都是 $O(\max_i-\max_{i-1})$ 的,所以在同一块中时间复杂度为 $O(\sqrt{n}\cdot(\max_i-\max_{i-1}))$。
将每一块 $L$ 的时间复杂度合在一起,可以得到:
对于 $L$ 的总时间复杂度为
$$
\begin{aligned}
& O(\sqrt{n}(\max{}_1-1)+\sqrt{n}(\max{}_2-\max{}_1)+\sqrt{n}(\max{}_3-\max{}_2)+\cdots+\sqrt{n}(\max{}_{\lceil\sqrt{n}\rceil}-\max{}_{\lceil\sqrt{n}\rceil-1))} \\
= \phantom{} & O(\sqrt{n}\cdot(\max{}_1-1+\max{}_2-\max{}_1+\max{}_3-\max{}_2+\cdots+\max{}_{\lceil\sqrt{n}\rceil-1}-\max{}_{\lceil\sqrt{n}\rceil-2}+\max{}_{\lceil\sqrt{n}\rceil}-\max{}_{\lceil\sqrt{n}\rceil-1)}) \\
= \phantom{} & O(\sqrt{n}\cdot(\max{}_{\lceil\sqrt{n}\rceil-1}))\\
\end{aligned}
$$
(裂项求和)
由题可知 $\max_{\lceil\sqrt{n}\rceil}$ 最大为 $n$,所以 $L$ 的总时间复杂度最坏情况下为 $O(n\sqrt{n})$。
综上所述,莫队算法的时间复杂度为 $O(n\sqrt{n})$;
但是对于 $m$ 的其他取值,如 $m<n$,分块方式需要改变才能变的更优。
怎么分块呢?
我们设块长度为 $S$,那么对于任意多个在同一块内的询问,挪动的距离就是 $n$,一共 $\displaystyle \frac{n}{S}$ 个块,移动的总次数就是 $\displaystyle \frac{n^2}{S}$,移动可能跨越块,所以还要加上一个 $mS$ 的复杂度,总复杂度为 $\displaystyle O\left(\frac{n^2}{S}+mS\right)$,我们要让这个值尽量小,那么就要将这两个项尽量相等,发现 $S$ 取 $\displaystyle \frac{n}{\sqrt{m}}$ 是最优的,此时复杂度为 $\displaystyle O\left(\frac{n^2}{\displaystyle \frac{n}{\sqrt{m}}}+m\left(\frac{n}{\sqrt{m}}\right)\right)=O(n\sqrt{m})$。
事实上,如果块长度的设定不准确,则莫队的时间复杂度会受到很大影响。例如,如果 $m$ 与 $\sqrt n$ 同阶,并且块长误设为 $\sqrt n$,则可以很容易构造出一组数据使其时间复杂度为 $O(n \sqrt n)$ 而不是正确的 $O(n)$。
莫队算法看起来十分暴力,很大程度上是因为莫队算法的分块排序方法看起来很粗糙。我们会想到通过看上去更精细的排序方法对所有区间排序。一种方法是把所有区间 $[l, r]$ 看成平面上的点 $(l, r)$,并对所有点建立曼哈顿最小生成树,每次沿着曼哈顿最小生成树的边在询问之间转移答案。这样看起来可以改善莫队算法的时间复杂度,但是实际上对询问分块排序的方法的时间复杂度上界已经是最优的了。
假设 $n, m$ 同阶且 $n$ 是完全平方数。我们考虑形如 $[a \sqrt n, b \sqrt n](1 \le a, b \le \sqrt n)$ 的区间,这样的区间一共有 $n$ 个。如果把所有的区间看成平面上的点,则两点之间的曼哈顿距离恰好为两区间的转移代价,并且任意两个区间之间的最小曼哈顿距离为 $\sqrt n$,所以处理所有询问的时间复杂度最小为 $O(n \sqrt n)$。其它情况的数据构造方法与之类似。
莫队算法还有一个特点:当 $n$ 不变时,$m$ 越大,处理每次询问的平均转移代价就越小。一些其他的离线算法也具有同样的特点(如求 LCA 的 Tarjan 算法),但是莫队算法的平均转移代价随 $m$ 的变化最明显。
## 例题 & 代码
???+ note " 例题 [「国家集训队」小 Z 的袜子](https://www.luogu.com.cn/problem/P1494)"
题目大意:
有一个长度为 $n$ 的序列 $\{c_i\}$。现在给出 $m$ 个询问,每次给出两个数 $l,r$,从编号在 $l$ 到 $r$ 之间的数中随机选出两个不同的数,求两个数相等的概率。
### 过程
思路:莫队算法模板题。
对于区间 $[l,r]$,以 $l$ 所在块的编号为第一关键字,$r$ 为第二关键字从小到大排序。
然后从序列的第一个询问开始计算答案,第一个询问通过直接暴力算出,复杂度为 $O(n)$,后面的询问在前一个询问的基础上得到答案。
具体做法:
对于区间 $[i,i]$,由于区间只有一个元素,我们很容易就能知道答案。然后一步一步从当前区间(已知答案)向下一个区间靠近。
我们设 $col[i]$ 表示当前颜色 $i$ 出现了多少次,$ans$ 当前共有多少种可行的配对方案(有多少种可以选到一双颜色相同的袜子),表示然后每次移动的时候更新答案——设当前颜色为 $k$,如果是增长区间就是 $ans$ 加上 $\dbinom{col[k]+1}{2}-\dbinom{col[k]}{2}$,如果是缩短就是 $ans$ 减去 $\dbinom{col[k]}{2}-\dbinom{col[k]-1}{2}$。
而这个询问的答案就是 $\displaystyle \frac{ans}{\dbinom{r-l+1}{2}}$。
这里有个优化:$\displaystyle \dbinom{a}{2}=\frac{a (a-1)}{2}$。
所以 $\displaystyle \dbinom{a+1}{2}-\dbinom{a}{2}=\frac{(a+1) a}{2}-\frac{a (a-1)}{2}=\frac{a}{2}\cdot (a+1-a+1)=\frac{a}{2}\cdot 2=a$。
所以 $\dbinom{col[k]+1}{2}-\dbinom{col[k]}{2}=col[k]$。
算法总复杂度:$O(n\sqrt{n} )$
下面的代码中 `deno` 表示答案的分母 (denominator),`nume` 表示分子 (numerator),`sqn` 表示块的大小:$\sqrt{n}$,`arr` 是输入的数组,`node` 是存储询问的结构体,`tab` 是询问序列(排序后的),`col` 同上所述。
**注意:由于 `++l` 和 `--r` 的存在,下面代码中的移动区间的 4 个 while 循环的位置很关键,不能随意改变它们之间的位置关系。**
??? note "关于四个循环位置的讨论"
莫队区间的移动过程,就相当于加入了 $[1,r]$ 的元素,并删除了 $[1,l-1]$ 的元素。因此,
- 对于 $l\le r$ 的情况,$[1,l-1]$ 的元素相当于被加入了一次又被删除了一次,$[l,r]$ 的元素被加入一次,$[r+1,+\infty)$ 的元素没有被加入。这个区间是合法区间。
- 对于 $l=r+1$ 的情况,$[1,r]$ 的元素相当于被加入了一次又被删除了一次,$[r+1,+\infty)$ 的元素没有被加入。这时这个区间表示空区间。
- 对于 $l>r+1$ 的情况,那么 $[r+1,l-1]$(这个区间非空)的元素被删除了一次但没有被加入,因此这个元素被加入的次数是负数。
因此,如果某时刻出现 $l>r+1$ 的情况,那么会存在一个元素,它的加入次数是负数。这在某些题目会出现问题,例如我们如果用一个 `set` 维护区间中的所有数,就会出现「需要删除 `set` 中不存在的元素」的问题。
代码中的四个 while 循环一共有 $4!=24$ 种排列顺序。不妨设第一个循环用于操作左端点,就有以下 $12$ 种排列(另外 $12$ 种是对称的)。下表列出了这 12 种写法的正确性,还给出了错误写法的反例。
| 循环顺序 | 正确性 | 反例或注释 |
| ----------------- | --- | ----------- |
| `l--,l++,r--,r++` | 错误 | $l<r<l'<r'$ |
| `l--,l++,r++,r--` | 错误 | $l<r<l'<r'$ |
| `l--,r--,l++,r++` | 错误 | $l<r<l'<r'$ |
| `l--,r--,r++,l++` | 正确 | 证明较繁琐 |
| `l--,r++,l++,r--` | 正确 | |
| `l--,r++,r--,l++` | 正确 | |
| `l++,l--,r--,r++` | 错误 | $l<r<l'<r'$ |
| `l++,l--,r++,r--` | 错误 | $l<r<l'<r'$ |
| `l++,r++,l--,r--` | 错误 | $l<r<l'<r'$ |
| `l++,r++,r--,l--` | 错误 | $l<r<l'<r'$ |
| `l++,r--,l--,r++` | 错误 | $l<r<l'<r'$ |
| `l++,r--,r++,l--` | 错误 | $l<r<l'<r'$ |
全部 24 种排列中只有 6 种是正确的,其中有 2 种的证明较繁琐,这里只给出其中 4 种的证明。
这 4 种正确写法的共同特点是,前两步先扩大区间(`l--` 或 `r++`),后两步再缩小区间(`l++` 或 `r--`)。这样写,前两步是扩大区间,可以保持 $l\le r+1$;执行完前两步后,$l\le l'\le r'\le r$ 一定成立,再执行后两步只会把区间缩小到 $[l',r']$,依然有 $l\le r+1$,因此这样写是正确的。
### 实现
??? 参考代码
```cpp
--8<-- "docs/misc/code/mo-algo/mo-algo_1.cpp"
#include <algorithm>
#include <cmath>
#include <cstdio>
using namespace std;
const int N = 50005;
int n, m, maxn;
int c[N];
long long sum;
int cnt[N];
long long ans1[N], ans2[N];
struct query {
int l, r, id;
bool operator<(const query &x) const { // 重载<运算符
if (l / maxn != x.l / maxn) return l < x.l;
return (l / maxn) & 1 ? r < x.r : r > x.r;
}
} a[N];
void add(int i) {
sum += cnt[i];
cnt[i]++;
}
void del(int i) {
cnt[i]--;
sum -= cnt[i];
}
long long gcd(long long a, long long b) { return b ? gcd(b, a % b) : a; }
int main() {
scanf("%d%d", &n, &m);
maxn = sqrt(n);
for (int i = 1; i <= n; i++) scanf("%d", &c[i]);
for (int i = 0; i < m; i++) scanf("%d%d", &a[i].l, &a[i].r), a[i].id = i;
sort(a, a + m);
for (int i = 0, l = 1, r = 0; i < m; i++) { // 具体实现
if (a[i].l == a[i].r) {
ans1[a[i].id] = 0, ans2[a[i].id] = 1;
continue;
}
while (l > a[i].l) add(c[--l]);
while (r < a[i].r) add(c[++r]);
while (l < a[i].l) del(c[l++]);
while (r > a[i].r) del(c[r--]);
ans1[a[i].id] = sum;
ans2[a[i].id] = (long long)(r - l + 1) * (r - l) / 2;
}
for (int i = 0; i < m; i++) {
if (ans1[i] != 0) {
long long g = gcd(ans1[i], ans2[i]);
ans1[i] /= g, ans2[i] /= g;
} else
ans2[i] = 1;
printf("%lld/%lld\n", ans1[i], ans2[i]);
}
return 0;
}```
## 普通莫队的优化
### 过程
我们看一下下面这组数据
```text
// 设块的大小为 2 (假设)
1 1
2 100
3 1
4 100
```
手动模拟一下可以发现,r 指针的移动次数大概为 300 次,我们处理完第一个块之后,$l = 2, r = 100$,此时只需要移动两次 l 指针就可以得到第四个询问的答案,但是我们却将 r 指针移动到 1 来获取第三个询问的答案,再移动到 100 获取第四个询问的答案,这样多了九十几次的指针移动。我们怎么优化这个地方呢?这里我们就要用到奇偶化排序。
什么是奇偶化排序?奇偶化排序即对于属于奇数块的询问,r 按从小到大排序,对于属于偶数块的排序,r 从大到小排序,这样我们的 r 指针在处理完这个奇数块的问题后,将在返回的途中处理偶数块的问题,再向 n 移动处理下一个奇数块的问题,优化了 r 指针的移动次数,一般情况下,这种优化能让程序快 30% 左右。
### 实现
排序代码:
压行
```cpp
// 这里有个小细节等下会讲
int unit; // 块的大小
struct node {
int l, r, id;
bool operator<(const node &x) const {
return l / unit == x.l / unit
? (r == x.r ? 0 : ((l / unit) & 1) ^ (r < x.r))
: l < x.l;
}
};
```
不压行
```cpp
struct node {
int l, r, id;
bool operator<(const node &x) const {
if (l / unit != x.l / unit) return l < x.l;
if ((l / unit) & 1)
return r <
x.r; // 注意这里和下面一行不能写小于(大于)等于,否则会出错(详见下面的小细节)
return r > x.r;
}
};
```
??? warning
小细节:如果使用 sort 比较两个函数,不能出现 $a < b$ 和 $b < a$ 同时为真的情况,否则会运行错误。
对于压行版,如果没有 `r == x.r` 的特判,当 l 属于同一奇数块且 r 相等时,会出现上面小细节中的问题(自己手动模拟一下),对于压行版,如果写成小于(大于)等于,则也会出现同样的问题。
## 参考资料
- [莫队算法学习笔记 | Sengxian's Blog](https://blog.sengxian.com/algorithms/mo-s-algorithm)
---
author: StudyingFather, Backl1ght, countercurrent-time, Ir1d, greyqz, MicDZ, ouuan, renbaoshuo
请确保您已经会普通莫队算法了。如果您还不会,请先阅读前面的 [普通莫队算法](./mo-algo.md)。
## 特点
普通莫队是不能带修改的。
我们可以强行让它可以修改,就像 DP 一样,可以强行加上一维 **时间维**, 表示这次操作的时间。
时间维表示经历的修改次数。
即把询问 $[l,r]$ 变成 $[l,r,\text{time}]$。
那么我们的坐标也可以在时间维上移动,即 $[l,r,\text{time}]$ 多了一维可以移动的方向,可以变成:
- $[l-1,r,\text{time}]$
- $[l+1,r,\text{time}]$
- $[l,r-1,\text{time}]$
- $[l,r+1,\text{time}]$
- $[l,r,\text{time}-1]$
- $[l,r,\text{time}+1]$
这样的转移也是 $O(1)$ 的,但是我们排序又多了一个关键字,再搞搞就行了。
可以用和普通莫队类似的方法排序转移,做到 $O(n^{5/3})$。
这一次我们排序的方式是以 $n^{2/3}$ 为一块,分成了 $n^{1/3}$ 块,第一关键字是左端点所在块,第二关键字是右端点所在块,第三关键字是时间。
???+ note "最优块长以及时间复杂度分析"
我们设序列长为 $n$,$m$ 个询问,$t$ 个修改。
带修莫队排序的第二关键字是右端点所在块编号,不同于普通莫队。
想一想,如果不把右端点分块:
- 乱序的右端点对于每个询问会移动 $n$ 次。
- 有序的右端点会带来乱序的时间,每次询问会移动 $t$ 次。
无论哪一种情况,带来的时间开销都无法接受。
接下来分析时间复杂度。
设块长为 $s$,则有 $\dfrac{n}{s}$ 个块。对于块 $i$ 和块 $j$,记有 $q_{i,j}$ 个询问的左端点位于块 $i$,右端点位于块 $j$。
每「组」左右端点不换块的询问 $(i,j)$,端点每次移动 $O(s)$ 次,时间单调递增,$O(t)$。
左右端点换块的时间忽略不计。
表示一下就是:
$$
\begin{aligned}
&\sum_{i=1}^{n/s}\sum_{j=i+1}^{n/s}(q_{i,j}\cdot s+t)\\
=&ms+\left(\dfrac{n}{s}\right)^2t\\
=&ms+\dfrac{n^2t}{s^2}
\end{aligned}
$$
考虑求导求此式极小值。设 $f(s)=ms+\dfrac{n^2t}{s^2}$。那 $f'(s)=m-\dfrac{2n^2t}{s^3}=0$。
得 $s=\sqrt[3]{\dfrac{2n^2t}{m}}=\dfrac{2^{1/3}n^{2/3}t^{1/3}}{m^{1/3}}=s_0$。
也就是当块长取 $\dfrac{n^{2/3}t^{1/3}}{m^{1/3}}$ 时有最优时间复杂度 $O\left(n^{2/3}m^{2/3}t^{1/3}\right)$。
常说的 $O\left(n^{5/3}\right)$ 便是把 $n,m,t$ 当做同数量级的时间复杂度。
实际操作中还是推荐设定 $n^{2/3}$ 为块长。
## 例题
???+ note " 例题 [「国家集训队」数颜色/维护队列](https://www.luogu.com.cn/problem/P1903)"
题目大意:给你一个序列,M 个操作,有两种操作:
1. 修改序列上某一位的数字
2. 询问区间 $[l,r]$ 中数字的种类数(多个相同的数字只算一个)
我们不难发现,如果不带操作 1(修改)的话,我们就能轻松用普通莫队解决。
但是题目还带单点修改,所以用 **带修改的莫队**。
### 过程
先考虑普通莫队的做法:
- 每次扩大区间时,每加入一个数字,则统计它已经出现的次数,如果加入前这种数字出现次数为 $0$,则说明这是一种新的数字,答案 $+1$。然后这种数字的出现次数 $+1$。
- 每次减小区间时,每删除一个数字,则统计它删除后的出现次数,如果删除后这种数字出现次数为 $0$,则说明这种数字已经从当前的区间内删光了,也就是当前区间减少了一种颜色,答案 $-1$。然后这种数字的出现次数 $-1$。
现在再来考虑修改:
- 单点修改,把某一位的数字修改掉。假如我们是从一个经历修改次数为 $i$ 的询问转移到一个经历修改次数为 $j$ 的询问上,且 $i<j$ 的话,我们就需要把第 $i+1$ 个到第 $j$ 个修改强行加上。
- 假如 $j<i$ 的话,则需要把第 $i$ 个到第 $j+1$ 个修改强行还原。
怎么强行加上一个修改呢?假设一个修改是修改第 $pos$ 个位置上的颜色,原本 $pos$ 上的颜色为 $a$,修改后颜色为 $b$,还假设当前莫队的区间扩展到了 $[l,r]$。
- 加上这个修改:我们首先判断 $pos$ 是否在区间 $[l,r]$ 内。如果是的话,我们等于是从区间中删掉颜色 $a$,加上颜色 $b$,并且当前颜色序列的第 $pos$ 项的颜色改成 $b$。如果不在区间 $[l,r]$ 内的话,我们就直接修改当前颜色序列的第 $pos$ 项为 $b$。
- 还原这个修改:等于加上一个修改第 $pos$ 项、把颜色 $b$ 改成颜色 $a$ 的修改。
因此这道题就这样用带修改莫队轻松解决啦!
### 实现
??? 参考代码
```cpp
--8<-- "docs/misc/code/modifiable-mo-algo/modifiable-mo-algo_1.cpp"
#include <bits/stdc++.h>
#define SZ (10005)
using namespace std;
template <typename _Tp>
void IN(_Tp& dig) {
char c;
dig = 0;
while (c = getchar(), !isdigit(c))
;
while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
}
int n, m, sqn, c[SZ], ct[SZ], c1, c2, mem[SZ][3], ans, tot[1000005], nal[SZ];
struct query {
int l, r, i, c;
bool operator<(const query another) const {
if (l / sqn == another.l / sqn) {
if (r / sqn == another.r / sqn) return i < another.i;
return r < another.r;
}
return l < another.l;
}
} Q[SZ];
void add(int a) {
if (!tot[a]) ans++;
tot[a]++;
}
void del(int a) {
tot[a]--;
if (!tot[a]) ans--;
}
char opt[10];
int main() {
IN(n), IN(m), sqn = pow(n, (double)2 / (double)3);
for (int i = 1; i <= n; i++) IN(c[i]), ct[i] = c[i];
for (int i = 1, a, b; i <= m; i++)
if (scanf("%s", opt), IN(a), IN(b), opt[0] == 'Q')
Q[c1].l = a, Q[c1].r = b, Q[c1].i = c1, Q[c1].c = c2, c1++;
else
mem[c2][0] = a, mem[c2][1] = ct[a], mem[c2][2] = ct[a] = b, c2++;
sort(Q, Q + c1), add(c[1]);
int l = 1, r = 1, lst = 0;
for (int i = 0; i < c1; i++) {
for (; lst < Q[i].c; lst++) {
if (l <= mem[lst][0] && mem[lst][0] <= r)
del(mem[lst][1]), add(mem[lst][2]);
c[mem[lst][0]] = mem[lst][2];
}
for (; lst > Q[i].c; lst--) {
if (l <= mem[lst - 1][0] && mem[lst - 1][0] <= r)
del(mem[lst - 1][2]), add(mem[lst - 1][1]);
c[mem[lst - 1][0]] = mem[lst - 1][1];
}
for (++r; r <= Q[i].r; r++) add(c[r]);
for (--r; r > Q[i].r; r--) del(c[r]);
for (--l; l >= Q[i].l; l--) add(c[l]);
for (++l; l < Q[i].l; l++) del(c[l]);
nal[Q[i].i] = ans;
}
for (int i = 0; i < c1; i++) printf("%d\n", nal[i]);
return 0;
}
```
---
author: StudyingFather, Backl1ght, countercurrent-time, Ir1d, greyqz, MicDZ, ouuan, Linky
## 括号序树上莫队
一般的莫队只能处理线性问题,我们要把树强行压成序列。
我们可以将树的括号序跑下来,把括号序分块,在括号序上跑莫队。
具体怎么做呢?
### 过程
dfs 一棵树,然后如果 dfs 到 x 点,就 `push_back(x)`,dfs 完 x 点,就直接 `push_back(-x)`,然后我们在挪动指针的时候,
- 新加入的值是 x --->`add(x)`
- 新加入的值是 - x --->`del(x)`
- 新删除的值是 x --->`del(x)`
- 新删除的值是 - x --->`add(x)`
这样的话,我们就把一棵树处理成了序列。
### 例题
???+ note " 例题 [「WC2013」糖果公园](https://uoj.ac/problem/58)"
题意:给你一棵树,树上第 $i$ 个点颜色为 $c_i$,每次询问一条路径 $u_i$,$v_i$, 求这条路径上的
$\sum_{c}val_c\sum_{i=1}^{cnt_c}w_i$
其中:$val$ 表示该颜色的价值,$cnt$ 表示颜色出现的次数,$w$ 表示该颜色出现 $i$ 次后的价值
#### 过程
先把树变成序列,然后每次添加/删除一个点,这个点的对答案的的贡献是可以在 $O(1)$ 时间内获得的,即 $val_c\times w_{cnt_{c+1}}$
发现因为他会把起点的子树也扫了一遍,产生多余的贡献,怎么办呢?
因为扫的过程中起点的子树里的点肯定会被扫两次,但贡献为 0。
所以可以开一个 $vis$ 数组,每次扫到点 x,就把 $vis_x$ 异或上 1。
如果 $vis_x=0$,那这个点的贡献就可以不计。
所以可以用树上莫队来求。
修改的话,加上一维时间维即可,变成带修改树上莫队。
然后因为所包含的区间内可能没有 LCA,对于没有的情况要将多余的贡献删除,然后就完事了。
#### 实现
??? 参考代码
```cpp
#include <algorithm>
#include <cmath>
#include <cstdio>
using namespace std;
const int maxn = 200010;
int f[maxn], g[maxn], id[maxn], head[maxn], cnt, last[maxn], dep[maxn],
fa[maxn][22], v[maxn], w[maxn];
int block, index, n, m, q;
int pos[maxn], col[maxn], app[maxn];
bool vis[maxn];
long long ans[maxn], cur;
struct edge {
int to, nxt;
} e[maxn];
int cnt1 = 0, cnt2 = 0; // 时间戳
struct query {
int l, r, t, id;
bool operator<(const query &b) const {
return (pos[l] < pos[b.l]) || (pos[l] == pos[b.l] && pos[r] < pos[b.r]) ||
(pos[l] == pos[b.l] && pos[r] == pos[b.r] && t < b.t);
}
} a[maxn], b[maxn];
void addedge(int x, int y) {
e[++cnt] = (edge){y, head[x]};
head[x] = cnt;
}
void dfs(int x) {
id[f[x] = ++index] = x;
for (int i = head[x]; i; i = e[i].nxt) {
if (e[i].to != fa[x][0]) {
fa[e[i].to][0] = x;
dep[e[i].to] = dep[x] + 1;
dfs(e[i].to);
}
}
id[g[x] = ++index] = x; // 括号序
}
int lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
if (dep[x] != dep[y]) {
int dis = dep[x] - dep[y];
for (int i = 20; i >= 0; i--)
if (dis >= (1 << i)) dis -= 1 << i, x = fa[x][i];
} // 爬到同一高度
if (x == y) return x;
for (int i = 20; i >= 0; i--) {
if (fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];
}
return fa[x][0];
}
void add(int x) {
if (vis[x])
cur -= (long long)v[col[x]] * w[app[col[x]]--];
else
cur += (long long)v[col[x]] * w[++app[col[x]]];
vis[x] ^= 1;
}
void modify(int x, int t) {
if (vis[x]) {
add(x);
col[x] = t;
add(x);
} else
col[x] = t;
} // 在时间维上移动
int main() {
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= m; i++) scanf("%d", &v[i]);
for (int i = 1; i <= n; i++) scanf("%d", &w[i]);
for (int i = 1; i < n; i++) {
int x, y;
scanf("%d%d", &x, &y);
addedge(x, y);
addedge(y, x);
}
for (int i = 1; i <= n; i++) {
scanf("%d", &last[i]);
col[i] = last[i];
}
dfs(1);
for (int j = 1; j <= 20; j++)
for (int i = 1; i <= n; i++)
fa[i][j] = fa[fa[i][j - 1]][j - 1]; // 预处理祖先
int block = pow(index, 2.0 / 3);
for (int i = 1; i <= index; i++) {
pos[i] = (i - 1) / block;
}
while (q--) {
int opt, x, y;
scanf("%d%d%d", &opt, &x, &y);
if (opt == 0) {
b[++cnt2].l = x;
b[cnt2].r = last[x];
last[x] = b[cnt2].t = y;
} else {
if (f[x] > f[y]) swap(x, y);
a[++cnt1] = (query){lca(x, y) == x ? f[x] : g[x], f[y], cnt2, cnt1};
}
}
sort(a + 1, a + cnt1 + 1);
int L, R, T; // 指针坐标
L = R = 0;
T = 1;
for (int i = 1; i <= cnt1; i++) {
while (T <= a[i].t) {
modify(b[T].l, b[T].t);
T++;
}
while (T > a[i].t) {
modify(b[T].l, b[T].r);
T--;
}
while (L > a[i].l) {
L--;
add(id[L]);
}
while (L < a[i].l) {
add(id[L]);
L++;
}
while (R > a[i].r) {
add(id[R]);
R--;
}
while (R < a[i].r) {
R++;
add(id[R]);
}
int x = id[L], y = id[R];
int llca = lca(x, y);
if (x != llca && y != llca) {
add(llca);
ans[a[i].id] = cur;
add(llca);
} else
ans[a[i].id] = cur;
}
for (int i = 1; i <= cnt1; i++) {
printf("%lld\n", ans[i]);
}
return 0;
}
```
## 真·树上莫队
上面的树上莫队只是将树转化成了链,下面的才是真正的树上莫队。
由于莫队相关的问题都是模板题,因此实现部分不做太多解释
### 询问的排序
首先我们知道莫队的是基于分块的算法,所以我们需要找到一种树上的分块方法来保证时间复杂度。
条件:
- 属于同一块的节点之间的距离不超过给定块的大小
- 每个块中的节点不能太多也不能太少
- 每个节点都要属于一个块
- 编号相邻的块之间的距离不能太大
了解了这些条件后,我们看到这样一道题 [「SCOI2005」王室联邦](https://loj.ac/problem/2152)。
在这道题的基础上我们只要保证最后一个条件就可以解决分块的问题了。
??? 思路
令 lim 为希望块的大小,首先,对于整个树 dfs,当子树的大小大于 lim 时,就将它们分在一块,容易想到:对于根,可能会剩下一些点,于是将这些点分在最后一个块里。
做法:用栈维护当前节点作为父节点访问它的子节点,当从栈顶到父节点的距离大于希望块的大小时,弹出这部分元素分为一块,最后剩余的一块单独作为一块。
最后的排序方法:若第一维时间戳大于第二维,交换它们,按第一维所属块为第一关键字,第二维时间戳为第二关键字排序。
### 指针的移动
#### 过程
容易想到,我们可以标记被计入答案的点,让指针直接向目标移动,同时取反路径上的点。
但是,这样有一个问题,若指针一开始都在 x 上,显然 x 被标记,当两个指针向同一子节点移动(还有许多情况)时,x 应该不被标记,但实际情况是 x 被标记,因为两个指针分别标记了一次,抵消了。
如何解决呢?
有一个很显然的性质:这些点肯定是某些 LCA,因为 LCA 处才有可能被重复撤销导致撤销失败。
所以我们每次不标记 LCA,到需要询问答案时再将 LCA 标记,然后再撤销。
#### 实现
```cpp
// 取反路径上除LCA以外的所有节点
void move(int x, int y) {
if (dp[x] < dp[y]) swap(x, y);
while (dp[x] > dp[y]) update(x), x = fa[x];
while (x != y) update(x), update(y), x = fa[x], y = fa[y];
// x!=y保证LCA没被取反
}
```
对于求 LCA,我们可以用树剖,然后我们就可以把分块的步骤放到树剖的第一次 dfs 里面,时间戳也可以直接用第二次 dfs 的 dfs 序。
```cpp
int bl[100002], bls = 0; // 属于的块,块的数量
unsigned step; // 块大小
int fa[100002], dp[100002], hs[100002] = {0}, sz[100002] = {0};
// 父节点,深度,重儿子,大小
stack<int> sta;
void dfs1(int x) {
sz[x] = 1;
unsigned ss = sta.size();
for (int i = head[x]; i; i = nxt[i])
if (ver[i] != fa[x]) {
fa[ver[i]] = x;
dp[ver[i]] = dp[x] + 1;
dfs1(ver[i]);
sz[x] += sz[ver[i]];
if (sz[ver[i]] > sz[hs[x]]) hs[x] = ver[i];
if (sta.size() - ss >= step) {
bls++;
while (sta.size() != ss) bl[sta.top()] = bls, sta.pop();
}
}
sta.push(x);
}
// main
if (!sta.empty()) {
bls++; // 这一行可写可不写
while (!sta.empty()) bl[sta.top()] = bls, sta.pop();
}
```
### 时间复杂度
重点到了,这里关系到块的大小取值。
设块的大小为 $unit$:
- 对于 x 指针,由于每个块中节点的距离在 $unit$ 左右,每个块中 x 指针移动 $unit^2$ 次($unit\times dis_{\max}$),共计 $n\times unit$ 次($unit^2 \times (\frac{n}{unit})$);
- 对于 y 指针,每个块中最多移动 $O(n)$ 次,共计 $\frac{n^2}{unit}$ 次($n \times (\frac{n}{unit})$)。
加起来大概在根号处取得最小值(由于树上莫队块的大小不固定,所以不一定要严格按照)。
### 例题「WC2013」糖果公园
由于多了时间维,块的大小取到 $n^{0.6}$ 的样子就差不多了。
??? 参考代码
```cpp
#include <bits/stdc++.h>
using namespace std;
int gi() {
int x, c, op = 1;
while (c = getchar(), c < '0' || c > '9')
if (c == '-') op = -op;
x = c ^ 48;
while (c = getchar(), c >= '0' && c <= '9')
x = (x << 3) + (x << 1) + (c ^ 48);
return x * op;
}
int head[100002], nxt[200004], ver[200004], tot = 0;
void add(int x, int y) {
ver[++tot] = y, nxt[tot] = head[x], head[x] = tot;
ver[++tot] = x, nxt[tot] = head[y], head[y] = tot;
}
int bl[100002], bls = 0;
unsigned step;
int fa[100002], dp[100002], hs[100002] = {0}, sz[100002] = {0}, top[100002],
id[100002];
stack<int> sta;
void dfs1(int x) {
sz[x] = 1;
unsigned ss = sta.size();
for (int i = head[x]; i; i = nxt[i])
if (ver[i] != fa[x]) {
fa[ver[i]] = x, dp[ver[i]] = dp[x] + 1;
dfs1(ver[i]);
sz[x] += sz[ver[i]];
if (sz[ver[i]] > sz[hs[x]]) hs[x] = ver[i];
if (sta.size() - ss >= step) {
bls++;
while (sta.size() != ss) bl[sta.top()] = bls, sta.pop();
}
}
sta.push(x);
}
int cnt = 0;
void dfs2(int x, int hf) {
top[x] = hf, id[x] = ++cnt;
if (!hs[x]) return;
dfs2(hs[x], hf);
for (int i = head[x]; i; i = nxt[i])
if (ver[i] != fa[x] && ver[i] != hs[x]) dfs2(ver[i], ver[i]);
}
int lca(int x, int y) {
while (top[x] != top[y]) {
if (dp[top[x]] < dp[top[y]]) swap(x, y);
x = fa[top[x]];
}
return dp[x] < dp[y] ? x : y;
}
struct qu {
int x, y, t, id;
bool operator<(const qu a) const {
return bl[x] == bl[a.x] ? (bl[y] == bl[a.y] ? t < a.t : bl[y] < bl[a.y])
: bl[x] < bl[a.x];
}
} q[100001];
int qs = 0;
struct ch {
int x, y, b;
} upd[100001];
int ups = 0;
long long ans[100001];
int b[100001] = {0};
int a[100001];
long long w[100001];
long long v[100001];
long long now = 0;
bool vis[100001] = {0};
void back(int t) {
if (vis[upd[t].x]) {
now -= w[b[upd[t].y]--] * v[upd[t].y];
now += w[++b[upd[t].b]] * v[upd[t].b];
}
a[upd[t].x] = upd[t].b;
}
void change(int t) {
if (vis[upd[t].x]) {
now -= w[b[upd[t].b]--] * v[upd[t].b];
now += w[++b[upd[t].y]] * v[upd[t].y];
}
a[upd[t].x] = upd[t].y;
}
void update(int x) {
if (vis[x])
now -= w[b[a[x]]--] * v[a[x]];
else
now += w[++b[a[x]]] * v[a[x]];
vis[x] ^= 1;
}
void move(int x, int y) {
if (dp[x] < dp[y]) swap(x, y);
while (dp[x] > dp[y]) update(x), x = fa[x];
while (x != y) update(x), update(y), x = fa[x], y = fa[y];
}
int main() {
int n = gi(), m = gi(), k = gi();
step = (int)pow(n, 0.6);
for (int i = 1; i <= m; i++) v[i] = gi();
for (int i = 1; i <= n; i++) w[i] = gi();
for (int i = 1; i < n; i++) add(gi(), gi());
for (int i = 1; i <= n; i++) a[i] = gi();
for (int i = 1; i <= k; i++)
if (gi())
q[++qs].x = gi(), q[qs].y = gi(), q[qs].t = ups, q[qs].id = qs;
else
upd[++ups].x = gi(), upd[ups].y = gi();
for (int i = 1; i <= ups; i++) upd[i].b = a[upd[i].x], a[upd[i].x] = upd[i].y;
for (int i = ups; i; i--) back(i);
fa[1] = 1;
dfs1(1), dfs2(1, 1);
if (!sta.empty()) {
bls++;
while (!sta.empty()) bl[sta.top()] = bls, sta.pop();
}
for (int i = 1; i <= n; i++)
if (id[q[i].x] > id[q[i].y]) swap(q[i].x, q[i].y);
sort(q + 1, q + qs + 1);
int x = 1, y = 1, t = 0;
for (int i = 1; i <= qs; i++) {
if (x != q[i].x) move(x, q[i].x), x = q[i].x;
if (y != q[i].y) move(y, q[i].y), y = q[i].y;
int f = lca(x, y);
update(f);
while (t < q[i].t) change(++t);
while (t > q[i].t) back(t--);
ans[q[i].id] = now;
update(f);
}
for (int i = 1; i <= qs; i++) printf("%lld\n", ans[i]);
return 0;
}
```
---
### 回滚莫队
author: StudyingFather, Backl1ght, countercurrent-time, Ir1d, greyqz, MicDZ, ouuan, YOYO-UIAT
## 引入
有些题目在区间转移时,可能会出现增加或者删除无法实现的问题。在只有增加不可实现或者只有删除不可实现的时候,就可以使用回滚莫队在 $O(n \sqrt m)$ 的时间内解决问题。回滚莫队的核心思想就是既然我只能实现一个操作,那么我就只使用一个操作,剩下的交给回滚解决。
回滚莫队分为只使用增加操作的回滚莫队和只使用删除操作的回滚莫队。以下仅介绍只使用增加操作的回滚莫队,只使用删除操作的回滚莫队和只使用增加操作的回滚莫队只在算法实现上有一点区别,故不再赘述。
## 例题 [JOISC 2014 Day1 历史研究](https://loj.ac/problem/2874)
给你一个长度为 $n$ 的数组 $A$ 和 $m$ 个询问 $(1 \leq n, m \leq 10^5)$,每次询问一个区间 $[L, R]$ 内重要度最大的数字,要求 **输出其重要度**。一个数字 $i$ 重要度的定义为 $i$ 乘上 $i$ 在区间内出现的次数。
在这个问题中,在增加的过程中更新答案是很好实现的,但是在删除的过程中更新答案是不好实现的。因为如果增加会影响答案,那么新答案必定是刚刚增加的数字的重要度,而如果删除过后区间重要度最大的数字改变,我们很难确定新的重要度最大的数字是哪一个。所以,普通的莫队很难解决这个问题。
## 过程
- 对原序列进行分块,对询问按以左端点所属块编号升序为第一关键字,右端点升序为第二关键字的方式排序。
- 按顺序处理询问:
- 如果询问左端点所属块 $B$ 和上一个询问左端点所属块的不同,那么将莫队区间的左端点初始化为 $B$ 的右端点加 $1$, 将莫队区间的右端点初始化为 $B$ 的右端点;
- 如果询问的左右端点所属的块相同,那么直接扫描区间回答询问;
- 如果询问的左右端点所属的块不同:
- 如果询问的右端点大于莫队区间的右端点,那么不断扩展右端点直至莫队区间的右端点等于询问的右端点;
- 不断扩展莫队区间的左端点直至莫队区间的左端点等于询问的左端点;
- 回答询问;
- 撤销莫队区间左端点的改动,使莫队区间的左端点回滚到 $B$ 的右端点加 $1$。
## 复杂度证明
假设回滚莫队的分块大小是 $b$:
- 对于左、右端点在同一个块内的询问,可以在 $O(b)$ 时间内计算;
- 对于其他询问,考虑左端点在相同块内的询问,它们的右端点单调递增,移动右端点的时间复杂度是 $O(n)$,而左端点单次询问的移动不超过 $b$,因为有 $\frac{n}{b}$ 个块,所以总复杂度是 $O(mb+\frac{n^2}{b})$,取 $b=\frac{n}{\sqrt{m}}$ 最优,时间复杂度为 $O(n\sqrt{m})$。
## 实现
??? 参考代码
```cpp
--8<-- "docs/misc/code/rollback-mo-algo/rollback-mo-algo_1.cpp"
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
int n, q;
int x[N], t[N], m;
struct Query {
int l, r, id;
} Q[N];
int pos[N], L[N], R[N], sz, tot;
int cnt[N], __cnt[N];
ll ans[N];
bool cmp(const Query& A, const Query& B) {
if (pos[A.l] == pos[B.l]) return A.r < B.r;
return pos[A.l] < pos[B.l];
}
void build() {
sz = sqrt(n);
tot = n / sz;
for (int i = 1; i <= tot; i++) {
L[i] = (i - 1) * sz + 1;
R[i] = i * sz;
}
if (R[tot] < n) {
++tot;
L[tot] = R[tot - 1] + 1;
R[tot] = n;
}
}
void Add(int v, ll& Ans) {
++cnt[v];
Ans = max(Ans, 1LL * cnt[v] * t[v]);
}
void Del(int v) { --cnt[v]; }
int main() {
scanf("%d %d", &n, &q);
for (int i = 1; i <= n; i++) scanf("%d", &x[i]), t[++m] = x[i];
for (int i = 1; i <= q; i++) scanf("%d %d", &Q[i].l, &Q[i].r), Q[i].id = i;
build();
// 对询问进行排序
for (int i = 1; i <= tot; i++)
for (int j = L[i]; j <= R[i]; j++) pos[j] = i;
sort(Q + 1, Q + 1 + q, cmp);
// 离散化
sort(t + 1, t + 1 + m);
m = unique(t + 1, t + 1 + m) - (t + 1);
for (int i = 1; i <= n; i++) x[i] = lower_bound(t + 1, t + 1 + m, x[i]) - t;
int l = 1, r = 0, last_block = 0, __l;
ll Ans = 0, tmp;
for (int i = 1; i <= q; i++) {
// 询问的左右端点同属于一个块则暴力扫描回答
if (pos[Q[i].l] == pos[Q[i].r]) {
for (int j = Q[i].l; j <= Q[i].r; j++) ++__cnt[x[j]];
for (int j = Q[i].l; j <= Q[i].r; j++)
ans[Q[i].id] = max(ans[Q[i].id], 1LL * t[x[j]] * __cnt[x[j]]);
for (int j = Q[i].l; j <= Q[i].r; j++) --__cnt[x[j]];
continue;
}
// 访问到了新的块则重新初始化莫队区间
if (pos[Q[i].l] != last_block) {
while (r > R[pos[Q[i].l]]) Del(x[r]), --r;
while (l < R[pos[Q[i].l]] + 1) Del(x[l]), ++l;
Ans = 0;
last_block = pos[Q[i].l];
}
// 扩展右端点
while (r < Q[i].r) ++r, Add(x[r], Ans);
__l = l;
tmp = Ans;
// 扩展左端点
while (__l > Q[i].l) --__l, Add(x[__l], tmp);
ans[Q[i].id] = tmp;
// 回滚
while (__l < l) Del(x[__l]), ++__l;
}
for (int i = 1; i <= q; i++) printf("%lld\n", ans[i]);
return 0;
}
```
## 参考资料
- [回滚莫队及其简单运用 | Parsnip's Blog](https://www.cnblogs.com/Parsnip/p/10969989.html)
---
### 二维莫队
二维莫队,顾名思义就是每个状态有四个方向可以扩展。
二维莫队每次移动指针要操作一行或者一列的数,具体实现方式与普通的一维莫队类似,这里不再赘述。这里重点讲块长选定部分。
## 块长选定
记询问次数为 $q$,当前矩阵的左上角坐标为 $(x_1,\ y_1)$,右下角坐标为 $(x_2,\ y_2)$,取块长为 $B$。
那么指针 $x_1$ 移动了 $\Theta(q\cdot B)$ 次,而指针 $y_2$ 移动了 $\Theta(n^4\cdot B^{-3})$ 次。
所以只需令 $q\cdot B=n^4\cdot B^{-3}$,即 $B=n\cdot q^{-\frac 14}$ 即可。
注意这样计算 $B$ 的结果 **可能为 $0$**,**注意特判**。
最终,计算部分时间复杂度是 $\Theta(n^2\cdot q^{\frac 34})$,加上对询问的排序过程,总时间复杂度为 $\Theta(n^2\cdot q^{\frac 34}+q\log q)$。
## 例题 1
???+ note "[BZOJ 2639 矩形计算](https://hydro.ac/d/bzoj/p/2639)"
输入一个 $n\times m$ 的矩阵,矩阵的每一个元素都是一个整数,然后有 $q$ 个询问,每次询问一个子矩阵的权值。矩阵的权值是这样定义的,对于一个整数 $x$,如果它在该矩阵中出现了 $p$ 次,那么它给该矩阵的权值就贡献 $p^2$。
数据范围:$1\leq n,\ m\leq 200$,$0\leq q\leq 10^5$,$|$ 矩阵元素大小 $| \leq 2\times 10^9$。
??? note "解题思路"
先离散化,二维莫队时用一个数组记录每个数当前出现的次数即可。
??? note "示例代码"
```cpp
--8<-- "docs/misc/code/mo-algo-2dimen/mo-algo-2dimen_1.cpp"
```
#include <bits/stdc++.h>
using namespace std;
int n, m, q, a[201][201];
long long ans[100001];
int disc[250001], cntdisc; // 离散化用
int blocklen, counts[40001];
long long now;
struct Question {
int x1, y1, x2, y2, qid;
bool operator<(Question tmp) const {
if (x1 / blocklen != tmp.x1 / blocklen) return x1 < tmp.x1;
if (y1 / blocklen != tmp.y1 / blocklen) return y1 < tmp.y1;
if (x2 / blocklen != tmp.x2 / blocklen) return x2 < tmp.x2;
return y2 < tmp.y2;
}
} Q[100001];
int Qcnt;
void mo_algo_row(int id, int val, int Y1, int Y2) {
for (int i = Y1; i <= Y2; i++)
now -= (long long)counts[a[id][i]] * counts[a[id][i]],
counts[a[id][i]] += val,
now += (long long)counts[a[id][i]] * counts[a[id][i]];
}
void mo_algo_column(int id, int val, int X1, int X2) {
for (int i = X1; i <= X2; i++)
now -= (long long)counts[a[i][id]] * counts[a[i][id]],
counts[a[i][id]] += val,
now += (long long)counts[a[i][id]] * counts[a[i][id]];
}
void mo_algo() {
blocklen = pow(n * m, 0.5) / pow(q, 0.25);
if (blocklen < 1) blocklen = 1;
sort(Q + 1, Q + 1 + Qcnt);
int X1 = 1, Y1 = 1, X2 = 0, Y2 = 0;
for (int i = 1; i <= Qcnt; i++) {
while (X1 > Q[i].x1) mo_algo_row(--X1, 1, Y1, Y2);
while (X2 < Q[i].x2) mo_algo_row(++X2, 1, Y1, Y2);
while (Y1 > Q[i].y1) mo_algo_column(--Y1, 1, X1, X2);
while (Y2 < Q[i].y2) mo_algo_column(++Y2, 1, X1, X2);
while (X1 < Q[i].x1) mo_algo_row(X1++, -1, Y1, Y2);
while (X2 > Q[i].x2) mo_algo_row(X2--, -1, Y1, Y2);
while (Y1 < Q[i].y1) mo_algo_column(Y1++, -1, X1, X2);
while (Y2 > Q[i].y2) mo_algo_column(Y2--, -1, X1, X2);
ans[Q[i].qid] = now;
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", a[i] + j), disc[++cntdisc] = a[i][j];
sort(disc + 1, disc + 1 + cntdisc);
cntdisc = unique(disc + 1, disc + cntdisc + 1) - disc - 1;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
a[i][j] = lower_bound(disc + 1, disc + 1 + cntdisc, a[i][j]) - disc;
scanf("%d", &q);
for (int i = 1; i <= q; i++) {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
if (x1 > x2) swap(x1, x2);
if (y1 > y2) swap(y1, y2);
Q[++Qcnt] = {x1, y1, x2, y2, i};
}
mo_algo();
for (int i = 1; i <= q; ++i) printf("%lld\n", ans[i]);
return 0;
}
## 例题 2
???+ note "[洛谷 P1527 \[国家集训队\] 矩阵乘法](https://www.luogu.com.cn/problem/P1527)"
给你一个 $n\times n$ 的矩阵,$q$ 次询问,每次询问一个子矩形的第 $k$ 小数。
数据范围:$1\leq n\leq 500$,$1\leq q\leq 6\times 10^4$,$0\leq a_{i,j}\leq 10^9$。
首先和上一题一样,需要离散化整个矩阵。但是需要注意,本题除了需要对数值进行分块,还需要对数值的值域进行分块,才能求出答案。
这里还需要用到奇偶化排序进行优化,具体内容请见 [普通莫队算法](../misc/mo-algo.md#普通莫队的优化)。
对于本题而言,时间限制不那么宽,注意代码常数的处理。取的块长计算值普遍较小,$n,\ q$ 都取最大值时块长大约在 $11$ 左右,可以直接设定为常数来节约代码耗时。
??? note "示例代码"
```cpp
--8<-- "docs/misc/code/mo-algo-2dimen/mo-algo-2dimen_2.cpp"
```
#include <bits/stdc++.h>
using namespace std;
void read(int& a) {
a = 0;
char c;
while ((c = getchar()) < 48)
;
do a = (a << 3) + (a << 1) + (c ^ 48);
while ((c = getchar()) > 47);
}
void write(int x) {
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
int n, q, a[501][501], ans[60001];
int disc[250001], cntdisc; // 离散化用
int nn;
int blockId[501], blocklen; // 分块
int rangeblockId[250001], rangeblocklen; // 值域分块
int counts[250001], countsum[501]; // 该值次数及值域块总和
struct Position {
int x, y;
};
vector<Position> pos[250001];
struct Question {
int x1, y1, x2, y2, k, qid;
bool operator<(Question tmp) const {
if (blockId[x1] != blockId[tmp.x1]) return blockId[x1] < blockId[tmp.x1];
if (blockId[y1] != blockId[tmp.y1])
return blockId[x1] & 1 ? y1 < tmp.y1 : y1 > tmp.y1;
if (blockId[y2] != blockId[tmp.y2])
return blockId[y1] & 1 ? y2 < tmp.y2 : y2 > tmp.y2;
else
return blockId[y2] & 1 ? x2 < tmp.x2 : x2 > tmp.x2;
}
} Q[60001];
int Qcnt;
void mo_algo() {
blocklen = 11;
for (int i = 1; i <= n; ++i) blockId[i] = (i - 1) / blocklen + 1;
rangeblocklen = n + 1;
for (int i = 1; i <= nn; ++i) rangeblockId[i] = (i - 1) / rangeblocklen + 1;
counts[a[1][1]] = countsum[rangeblockId[a[1][1]]] = 1;
sort(Q + 1, Q + 1 + Qcnt);
int L = 1, R = 1, D = 1, U = 1;
for (int i = 1; i <= q; ++i) {
while (R < Q[i].y2) {
++R;
for (int i = U; i <= D; ++i)
++counts[a[i][R]], ++countsum[rangeblockId[a[i][R]]];
}
while (L > Q[i].y1) {
--L;
for (int i = U; i <= D; ++i)
++counts[a[i][L]], ++countsum[rangeblockId[a[i][L]]];
}
while (D < Q[i].x2) {
++D;
for (int i = L; i <= R; ++i)
++counts[a[D][i]], ++countsum[rangeblockId[a[D][i]]];
}
while (U > Q[i].x1) {
--U;
for (int i = L; i <= R; ++i)
++counts[a[U][i]], ++countsum[rangeblockId[a[U][i]]];
}
while (R > Q[i].y2) {
for (int i = U; i <= D; ++i)
--counts[a[i][R]], --countsum[rangeblockId[a[i][R]]];
--R;
}
while (L < Q[i].y1) {
for (int i = U; i <= D; ++i)
--counts[a[i][L]], --countsum[rangeblockId[a[i][L]]];
++L;
}
while (D > Q[i].x2) {
for (int i = L; i <= R; ++i)
--counts[a[D][i]], --countsum[rangeblockId[a[D][i]]];
--D;
}
while (U < Q[i].x1) {
for (int i = L; i <= R; ++i)
--counts[a[U][i]], --countsum[rangeblockId[a[U][i]]];
++U;
}
int res = 1, cnt = 0;
while (cnt + countsum[res] < Q[i].k && res <= rangeblockId[nn])
cnt += countsum[res], ++res;
res = (res - 1) * rangeblocklen + 1;
while (cnt + counts[res] < Q[i].k && res <= nn) cnt += counts[res], ++res;
ans[Q[i].qid] = disc[res];
}
}
int main() {
read(n);
read(q);
nn = n * n;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j) {
int x;
read(x);
a[i][j] = disc[++cntdisc] = x;
}
sort(disc + 1, disc + 1 + cntdisc);
cntdisc = unique(disc + 1, disc + cntdisc + 1) - disc - 1;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
a[i][j] = lower_bound(disc + 1, disc + 1 + cntdisc, a[i][j]) - disc;
for (int i = 1; i <= q; ++i) {
int x1, y1, x2, y2, k;
read(x1);
read(y1);
read(x2);
read(y2);
read(k);
Q[++Qcnt] = {x1, y1, x2, y2, k, i};
}
mo_algo();
for (int i = 1; i <= q; ++i) write(ans[i]), puts("");
return 0;
}
```
### 二次离线莫队
author: Lyccrius
## 例题 1
???+ note "[Luogu P5047 \[Ynoi2019 模拟赛\] Yuno loves sqrt technology II](https://www.luogu.com.cn/problem/P5047)"
给你一个长为 $n$ 的序列 $a$,$m$ 次询问,每次查询一个区间的逆序对数。
数据范围:$1 \leq n,m \leq 10^5$,$0 \leq a_i \leq 10^9$。
查询区间逆序对数,在使用莫队的同时维护一颗权值线段树或权值树状数组,可以在 $O(n \sqrt n \log n)$ 的时间复杂度内解决该问题。当然,取块长 $T = \sqrt {n \log n}$ 更优。
可是这样的复杂度仍然无法达到毒瘤出题人的要求,我们需要在此算法上进一步优化。
考虑该题与其它使用莫队的题的差异性,由于需要在维护值域的数据结构上查询,故单次端点的移动是 $O(\log n)$ 而非 $O(1)$。
众所周知,莫队是一种离线算法,它通过将询问离线处理的方式来优化复杂度。我们在将原问题的查询离线的基础上,尝试将端点移动时在数据结构上进行的修改和查询操作离线下来统一处理,最后用 $O(n \sqrt n + n \log n)$ 的时间复杂度解决问题。由于前后进行了两次离线操作,故称为「莫队二次离线」。
## 例题 2
???+ note "[Luogu P5501 \[LnOI2019\] 来者不拒,去者不追](https://www.luogu.com.cn/problem/P5501)"
给定一个长度为 $n$ 的序列 $a$。给定 $m$ 个询问,每次询问一个区间中 $[l, r]$ 中所有数的「Abbi 值」之和。
Abbi 值定义为:若 $a_i$ 在询问区间 $[l, r]$ 中是第 $k$ 小,那么它的「Abbi 值」等于 $k \times a_i$。
数据范围:$1 \leq a_i \leq 100000$,$1 \leq l \leq r \leq n$,$1\leq n, m\leq 500000$。
??? note "示例代码"
```cpp
--8<-- "docs/misc/code/mo-algo-secondary-offline/mo-algo-secondary-offline_1.cpp"
```
```cpp
#include <algorithm>
#include <iostream>
#include <vector>
typedef long long lxl;
const int maxN = 5e5;
const int maxM = 5e5;
const int maxA = 1e5;
const int sqrN = 708;
const int sqrA = 317;
int n, m;
int a[maxN + 10];
int b[maxN + 10];
int l, r;
lxl f[maxN + 10];
lxl g[maxN + 10];
lxl ans[maxM + 10];
typedef struct SegmentTree {
struct Node {
lxl val;
lxl tag;
} node[4 * maxA + 10];
void MakeTag(int u, int l, int r, lxl val) {
node[u].val += val * (r - l + 1);
node[u].tag += val;
return;
}
void PushDown(int u, int l, int r) {
if (!node[u].tag) return;
int mid = (l + r) / 2;
MakeTag(2 * u, l, mid, node[u].tag);
MakeTag(2 * u + 1, mid + 1, r, node[u].tag);
node[u].tag = 0;
return;
}
void PushUp(int u) {
node[u].val = node[2 * u].val + node[2 * u + 1].val;
return;
}
void Add(int u, int l, int r, int s, int t, lxl val) {
if (s > t) return;
if (s <= l && r <= t) {
MakeTag(u, l, r, val);
return;
}
PushDown(u, l, r);
int mid = (l + r) / 2;
if (s <= mid) Add(2 * u, l, mid, s, t, val);
if (t >= mid + 1) Add(2 * u + 1, mid + 1, r, s, t, val);
PushUp(u);
return;
}
void Add(int u, int l, int r, int pos, lxl val) {
Add(u, l, r, pos, pos, val);
return;
}
lxl Ask(int u, int l, int r, int s, int t) {
if (s > t) return 0;
if (s <= l && r <= t) {
return node[u].val;
}
PushDown(u, l, r);
int mid = (l + r) / 2;
if (t <= mid) return Ask(2 * u, l, mid, s, t);
if (s >= mid + 1) return Ask(2 * u + 1, mid + 1, r, s, t);
return Ask(2 * u, l, mid, s, t) + Ask(2 * u + 1, mid + 1, r, s, t);
}
} sgt;
typedef struct BlockArray {
struct Block {
int l, r;
lxl tag;
} block[sqrA + 10];
struct Array {
int bel;
lxl val;
} array[maxA + 10];
void Build() {
for (int i = 1; i <= maxA; i++) array[i].bel = (i - 1) / sqrA + 1;
for (int i = 1; i <= maxA; i++) block[array[i].bel].r = i;
for (int i = maxA; i >= 1; i--) block[array[i].bel].l = i;
return;
}
void Add(int pos, lxl val) {
for (int i = array[pos].bel + 1; i <= array[maxA].bel; i++)
block[i].tag += val;
for (int i = pos; i <= block[array[pos].bel].r; i++) array[i].val += val;
return;
}
lxl Ask(int pos) { return array[pos].val + block[array[pos].bel].tag; }
lxl Ask(int l, int r) {
if (l > r) return 0;
return Ask(r) - Ask(l - 1);
}
} dba;
namespace captainMoSecondaryOffline {
namespace offline2 {
struct Query {
int i;
int l, r;
int k;
};
std::vector<Query> query[maxN + 10];
dba sum, cnt;
void solve() {
sum.Build();
cnt.Build();
for (int i = 1; i <= n; i++) {
sum.Add(a[i], a[i]);
cnt.Add(a[i], 1);
for (int j = 0; j < query[i].size(); j++) {
for (int k = query[i][j].l; k <= query[i][j].r; k++) {
ans[query[i][j].i] +=
1ll * query[i][j].k *
(sum.Ask(a[k] + 1, maxA) + cnt.Ask(1, a[k] - 1) * a[k]);
}
}
}
return;
}
} // namespace offline2
namespace offline1 {
struct Query {
int i;
int l, r;
bool operator<(const Query &other) const {
if (b[l] != b[other.l]) return l < other.l;
return r < other.r;
}
};
std::vector<Query> query;
sgt sum, cnt;
void solve() {
std::sort(query.begin(), query.end());
for (int i = 1; i <= n; i++) {
f[i] = sum.Ask(1, 1, maxA, a[i] + 1, maxA);
g[i] = cnt.Ask(1, 1, maxA, 1, a[i] - 1);
sum.Add(1, 1, maxA, a[i], a[i]);
cnt.Add(1, 1, maxA, a[i], 1);
}
for (int i = 0, l = 1, r = 0; i < query.size(); i++) {
if (l > query[i].l) {
offline2::query[r].push_back(
(offline2::Query){query[i].i, query[i].l, l - 1, 1});
while (l > query[i].l) {
l--;
ans[query[i].i] -= f[l] + (g[l] - 1) * a[l];
}
}
if (r < query[i].r) {
offline2::query[l - 1].push_back(
(offline2::Query){query[i].i, r + 1, query[i].r, -1});
while (r < query[i].r) {
r++;
ans[query[i].i] += f[r] + (g[r] + 1) * a[r];
}
}
if (l < query[i].l) {
offline2::query[r].push_back(
(offline2::Query){query[i].i, l, query[i].l - 1, -1});
while (l < query[i].l) {
ans[query[i].i] += f[l] + (g[l] - 1) * a[l];
l++;
}
}
if (r > query[i].r) {
offline2::query[l - 1].push_back(
(offline2::Query){query[i].i, query[i].r + 1, r, 1});
while (r > query[i].r) {
ans[query[i].i] -= f[r] + (g[r] + 1) * a[r];
r--;
}
}
}
return;
}
} // namespace offline1
void solve() {
offline1::solve();
offline2::solve();
for (int i = 0; i < m; i++)
ans[offline1::query[i].i] += ans[offline1::query[i - 1].i];
return;
}
} // namespace captainMoSecondaryOffline
int main() {
std::cin >> n >> m;
for (int i = 1; i <= n; i++) std::cin >> a[i];
for (int i = 1; i <= n; i++) b[i] = (i - 1) / sqrN + 1;
for (int i = 1; i <= m; i++)
std::cin >> l >> r,
captainMoSecondaryOffline::offline1::query.push_back(
(captainMoSecondaryOffline::offline1::Query){i, l, r});
captainMoSecondaryOffline::solve();
for (int i = 1; i <= m; i++) std::cout << ans[i] << '\n';
return 0;
}
```
---
### 莫队配合bitset
author: StudyingFather, Backl1ght, countercurrent-time, Ir1d, greyqz, MicDZ, ouuan
bitset 常用于常规数据结构难以维护的的判定、统计问题,而莫队可以维护常规数据结构难以维护的区间信息。把两者结合起来使用可以同时利用两者的优势。
## 例题 [「Ynoi2016」掉进兔子洞](https://www.luogu.com.cn/problem/P4688)
本题刚好符合上面提到的莫队配合 bitset 的特征。不难想到我们可以分别用 bitset 存储每一个区间内的出现过的所有权值,一组询问的答案即所有区间的长度和减去三者的并集元素个数 $\times 3$。
但是在莫队中使用 bitset 也需要针对 bitset 的特性调整算法:
1. bitset 不能很好地处理同时出现多个权值的情况。我们可以把当前元素离散化后的权值与当前区间的的出现次数之和作为往 bitset 中插入的对象。
2. 我们平常使用莫队时,可能会不注意 4 种移动指针的方法顺序,所以指针移动的过程中可能会出现区间的左端点在右端点右边,区间长度为负值的情况,导致元素的个数为负数。这在其他情况下并没有什么影响,但是本题中在 bitset 中插入的元素与元素个数有关,所以我们需要注意 4 种移动指针的方法顺序,将左右指针分别往左边和右边移动的语句写在前面,避免往 bitset 中插入负数。
3. 虽然 bitset 用空间小,但是仍然难以承受 $10 ^ 5 \times 10 ^ 5$ 的数据规模。所以我们需要将询问划分成常数块分别处理,保证空间刚好足够的情况下时间复杂度不变。
??? 参考代码
```cpp
--8<-- "docs/misc/code/mo-algo-with-bitset/mo-algo-with-bitset_1.cpp"
#include <algorithm>
#include <bitset>
#include <cmath>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 100005, M = N / 3 + 10;
int n, m, maxn;
int a[N], ans[M], cnt[N];
bitset<N> sum[M], now;
struct query {
int l, r, id;
bool operator<(const query& x) const {
if (l / maxn != x.l / maxn) return l < x.l;
return (l / maxn) & 1 ? r < x.r : r > x.r;
}
} q[M * 3];
void static_set() {
static int tmp[N];
memcpy(tmp, a, sizeof(a));
sort(tmp + 1, tmp + n + 1);
for (int i = 1; i <= n; i++)
a[i] = lower_bound(tmp + 1, tmp + n + 1, a[i]) - tmp;
}
void add(int x) {
now.set(x + cnt[x]);
cnt[x]++;
}
void del(int x) {
cnt[x]--;
now.reset(x + cnt[x]);
}
void solve() {
int cnt = 0, tot = 0;
now.reset();
for (tot = 0; tot < M - 5 && m; tot++) {
m--;
ans[tot] = 0;
sum[tot].set();
for (int j = 0; j < 3; j++) {
scanf("%d%d", &q[cnt].l, &q[cnt].r);
q[cnt].id = tot;
ans[tot] += q[cnt].r - q[cnt].l + 1;
cnt++;
}
}
sort(q, q + cnt);
for (int i = 0, l = 1, r = 0; i < cnt; i++) {
while (l > q[i].l) add(a[--l]);
while (r < q[i].r) add(a[++r]);
while (l < q[i].l) del(a[l++]);
while (r > q[i].r) del(a[r--]);
sum[q[i].id] &= now;
}
for (int i = 0; i < tot; i++)
printf("%d\n", ans[i] - (int)sum[i].count() * 3);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
static_set();
maxn = sqrt(n);
solve();
memset(cnt, 0, sizeof(cnt));
solve();
memset(cnt, 0, sizeof(cnt));
solve();
return 0;
}```
## 习题
- [小清新人渣的本愿](https://www.luogu.com.cn/problem/P3674)
- [「Ynoi2017」由乃的玉米田](https://www.luogu.com.cn/problem/P5355)
- [「Ynoi2011」WBLT](https://www.luogu.com.cn/problem/P5313)
























 7336
7336

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










