定义 f ( x ) = a 0 + a 1 x 1 + . . . . + a n − 1 x n − 1 = ∑ i = 0 n − 1 a i x i f(x) = a_0 + a_1x^1+....+a_{n-1}x^{n-1}=\sum_{i=0}^{n-1} a_ix^i f(x)=a0+a1x1+....+an−1xn−1=∑i=0n−1aixi,这个就是 n n n项 n − 1 n - 1 n−1次多项式。
多项式的项数取决于有几个次数互不相同的单项式。次数取决于最高的次方。比如上面这个例子:有 n n n项,最高次方的数字是 x n − 1 x^{n-1} xn−1。所以他就是 n n n项 n − 1 n-1 n−1次多项式。
FFT就是处理两个多项式的乘积。暴力的话复杂度为 O ( n 2 ) O(n^2) O(n2),FFT能降到 O ( n l o g n ) O(n log n) O(nlogn)
复数就是 a + b i a + bi a+bi,其中, i = − 1 , i 2 = − 1 i = \sqrt{-1},i^2 = -1 i=−1,i2=−1。我们称 a a a为实部, b i bi bi为虚部。通常用 z z z表示复数
加法:
(
a
+
b
i
)
+
(
c
+
d
i
)
=
a
+
b
i
+
c
+
d
i
=
a
+
c
+
b
i
+
d
i
=
(
a
+
c
)
+
i
(
b
+
d
)
\begin{array}{c} (a + bi) + (c + di) \cr \newline = a + bi + c + di \cr \newline = a + c + bi + di \cr \newline = (a + c) + i(b + d) \end{array}
(a+bi)+(c+di)=a+bi+c+di=a+c+bi+di=(a+c)+i(b+d)
实部相加,虚部相加
减法:
(
a
+
b
i
)
−
(
c
+
d
i
)
=
a
+
b
i
−
c
−
d
i
=
a
−
c
+
b
i
−
d
i
=
(
a
−
c
)
+
i
(
b
−
d
)
\begin{array}{c} (a + bi) - (c + di) \cr \newline = a + bi - c - di \cr \newline = a - c + bi - di \cr \newline = (a - c) + i(b - d) \end{array}
(a+bi)−(c+di)=a+bi−c−di=a−c+bi−di=(a−c)+i(b−d)
实部相减,虚部相减
乘法:
(
a
+
b
i
)
(
c
+
d
i
)
=
a
c
+
c
b
i
+
a
d
i
+
b
d
i
2
=
a
c
+
i
(
a
d
+
b
c
)
+
(
−
1
×
b
d
)
=
a
c
+
i
(
a
d
+
b
c
)
−
b
d
=
(
a
c
−
b
d
)
+
i
(
a
d
+
b
c
)
\begin{array}{c} (a+bi)(c+di) \cr \newline =ac + cbi + adi + bdi^2 \cr \newline = ac + i(ad + bc) + (-1 \times bd) \cr \newline =ac + i(ad+bc)-bd \cr \newline =(ac-bd)+ i(ad+bc) \end{array}
(a+bi)(c+di)=ac+cbi+adi+bdi2=ac+i(ad+bc)+(−1×bd)=ac+i(ad+bc)−bd=(ac−bd)+i(ad+bc)
除法:
共轭复数是一个很重要的知识。
a
+
b
i
a + bi
a+bi的共轭复数为
a
−
b
i
a-bi
a−bi(类似于共轭根式)。
(
a
+
b
i
)
(
a
−
b
i
)
=
a
2
−
(
b
i
)
2
=
a
2
−
(
−
1
×
b
2
)
=
a
2
+
b
2
\begin{array}{c} (a+bi)(a-bi) \cr \newline =a^2-(bi)^2 \cr \newline = a^2-(-1\times b^2) \cr \newline =a^2+b^2 \end{array}
(a+bi)(a−bi)=a2−(bi)2=a2−(−1×b2)=a2+b2
通常记作
z
ˉ
\bar{z}
zˉ。
下面是两个复数
x
x
x和
y
y
y的除法
x
÷
y
=
x
y
=
x
y
ˉ
y
y
ˉ
=
(
a
+
b
i
)
(
c
−
d
i
)
c
2
+
d
2
\begin{array}{c} x \div y \cr \newline =\dfrac{x}{y} \cr \newline =\dfrac{x\bar{y}}{y\bar{y}} \cr \newline =\dfrac{(a + bi)(c - di)}{c^2 + d^2} \end{array}
x÷y=yx=yyˉxyˉ=c2+d2(a+bi)(c−di)
由于
c
2
+
d
2
c^2+d^2
c2+d2为有理数,所以我们把这个过程称作分母有理化
在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称直角坐标系——百度百科
通常,一个点可以表示为 P ( x , y ) P(x,y) P(x,y)。其中, P P P表示点的名字, ( x , y ) (x,y) (x,y)表示这个点的坐标。
例如,上面的例子就是 A ( 5 , 5 ) A(5,5) A(5,5)
e
i
θ
=
c
o
s
θ
+
i
×
s
i
n
θ
e^{i\theta} = cos \theta + i\times sin \theta
eiθ=cosθ+i×sinθ
其中,
r
r
r表示模长,
θ
\theta
θ表示辐角。
a
+
b
i
=
r
×
(
c
o
s
θ
+
i
×
s
i
n
θ
)
=
r
e
i
θ
a + bi =r \times (cos \theta + i\times sin \theta) =re^{i\theta}
a+bi=r×(cosθ+i×sinθ)=reiθ
丧心病狂的· 证明:
c
o
s
x
=
∑
i
=
0
∞
x
2
i
(
2
i
)
2
×
(
−
1
)
i
=
1
−
x
2
2
!
+
x
4
4
!
−
.
.
.
s
i
n
x
=
∑
i
=
0
∞
x
2
i
+
1
(
2
i
+
1
)
2
×
(
−
1
)
i
=
x
−
x
3
3
!
+
x
5
5
!
−
.
.
.
e
x
=
∑
i
=
0
∞
x
n
n
!
\begin{array}{c} cos\ x = \sum^{\infty}_{i=0}\dfrac{x^{2i}}{(2i)^2} \times (-1)^i = 1 - \dfrac{x^2}{2!}+\dfrac{x^4}{4!}-... \cr \newline sin\ x = \sum^{\infty}_{i=0}\dfrac{x^{2i + 1}}{(2i + 1)^2} \times (-1)^i=x - \dfrac{x^3}{3!}+\dfrac{x^5}{5!}-... \cr \newline e^x = \sum^{\infty}_{i = 0}\dfrac{x^n}{n!} \end{array}
cos x=∑i=0∞(2i)2x2i×(−1)i=1−2!x2+4!x4−...sin x=∑i=0∞(2i+1)2x2i+1×(−1)i=x−3!x3+5!x5−...ex=∑i=0∞n!xn
将
x
x
x带入
i
θ
i\theta
iθ.
e
i
θ
=
1
+
i
θ
+
(
i
θ
)
2
2
!
+
(
i
θ
)
3
3
!
+
.
.
.
e^{i\theta} = 1 + {i\theta} + \dfrac{(i\theta)^2}{2!}+\dfrac{(i\theta)^3}{3!}+...
eiθ=1+iθ+2!(iθ)2+3!(iθ)3+...
=
(
1
−
θ
2
2
!
+
θ
4
4
!
−
.
.
.
)
+
(
θ
−
θ
3
3
!
+
θ
5
5
!
−
.
.
.
)
\ \ \ \ \ \ = (1 - \dfrac{\theta^2}{2!} + \dfrac{\theta^4}{4!} -...) + (\theta - \dfrac{\theta^3}{3!} + \dfrac{\theta^5}{5!} - ...)
=(1−2!θ2+4!θ4−...)+(θ−3!θ3+5!θ5−...)
=
c
o
s
θ
+
i
s
i
n
θ
\ \ \ \ \ \ =cos\ \theta + isin\ \theta
=cos θ+isin θ
首先这是个圆,它的半径是一,所以称为单位圆.
如果有一个复数 w w w满足 w n = 1 w^n=1 wn=1称 w w w是 n n n次单位根。
当 n = 3 n = 3 n=3, w 1 = 1 , w 2 , 3 = 1 ± 3 i 2 w_1=1,w_{2,3}=\dfrac{1\pm\sqrt{3}i}{2} w1=1,w2,3=21±3i。
n n n次单位根就是将单位圆等分成 n n n份,对应的数既是分割后的点对应的数。
我们记第 k k k个 n n n次单位根为 w n k w_n^k wnk,保证 ∑ i = 0 n − 1 w n i \sum^{n-1}_{i=0}w_n^i ∑i=0n−1wni互不相同。
性质:
1.
w
2
n
2
k
=
w
n
k
1.w^{2k}_{2n} = w^k_n
1.w2n2k=wnk
2.
w
n
k
=
−
w
n
k
+
n
2
2.w^k_n=-w^{k+\frac{n}{2}}_{n}
2.wnk=−wnk+2n
还有一个快速求
w
n
k
w^k_n
wnk的方法,用到欧拉公式(下面是用弧度制,
π
=
18
0
∘
,
2
π
=
36
0
∘
\pi = 180^\circ,2\pi=360^\circ
π=180∘,2π=360∘)。
w n k = e 2 k i π π = c o s 2 k π n + i × s i n 2 k π n w^k_n=e^{\frac{2ki\pi}{\pi}} = cos\dfrac{2k\pi}{n} + i\times sin\dfrac{2k\pi}{n} wnk=eπ2kiπ=cosn2kπ+i×sinn2kπ
还记得 f ( x ) = a 0 + a 1 x 1 + . . . . + a n x n = ∑ i = 1 n a i x i f(x) = a_0 + a_1x^1+....+a_nx^n=\sum_{i=1}^{n} a_ix^i f(x)=a0+a1x1+....+anxn=∑i=1naixi吗,系数表示法就是讲系数单独抽出来,就是 f ( x ) = { a 0 , a 1 , a 2 , . . . , a n } f(x)=\{a_0,a_1,a_2,...,a_n\} f(x)={a0,a1,a2,...,an}
- 把多项式放到平面直角坐标系里面,看成一个函数
- 把 n n n个不同的 x x x代入,会得出 n n n个不同的 y y y,在坐标系内就是 n n n个不同的点
- 那么这 n n n个点唯一确定该多项式,也就是有且仅有一个多项式满足 ∀ k , f ( x k ) = y k \forall k,f(x_k) = y_k ∀k,f(xk)=yk
- 理由很简单,把 n n n条式子联立起来成为一个有 n n n条方程的 n n n元方程组,每一项的系数都可以解出来
所以 f ( x ) = { ( x 0 , f ( x 0 ) , ( x 1 , f ( x 1 ) , . . , ( x n , f ( x n ) } f(x) = \{(x_0,f(x_0),(x_1,f(x_1),..,(x_n,f(x_n)\} f(x)={(x0,f(x0),(x1,f(x1),..,(xn,f(xn)}.
首先,
f
(
x
)
=
a
0
+
a
1
x
1
+
.
.
.
.
+
a
n
−
1
x
n
−
1
=
(
a
0
+
a
2
x
2
+
.
.
.
+
a
n
−
2
x
n
−
2
)
+
(
a
1
x
+
a
3
x
3
+
.
.
.
+
a
n
−
1
x
n
−
1
)
=
(
a
0
+
a
2
x
2
+
.
.
.
+
a
n
−
2
x
n
−
2
)
+
x
(
a
1
+
a
3
x
2
+
.
.
.
+
a
n
−
1
x
n
−
2
)
\begin{array}{c} f(x) =a_0 + a_1x^1+....+a_{n-1}x^{n-1} \cr \newline = (a_0 + a_2x^2+...+a_{n-2}x^{n-2})+(a1x+a_3x^3+...+a_{n-1}x^{n-1}) \cr \newline = (a_0 + a_2x^2+...+a_{n-2}x^{n-2}) + x(a1+a_3x^2+...+a_{n-1}x^{n-2}) \end{array}
f(x)=a0+a1x1+....+an−1xn−1=(a0+a2x2+...+an−2xn−2)+(a1x+a3x3+...+an−1xn−1)=(a0+a2x2+...+an−2xn−2)+x(a1+a3x2+...+an−1xn−2)
我们发现,前面这个式子和后面这个式子几乎一样。
不妨再设两个多项式
f
1
(
x
)
,
f
2
(
x
)
f_1(x),f_2(x)
f1(x),f2(x),令
f
1
(
x
)
=
(
a
0
+
a
2
x
+
a
4
x
2
+
.
.
.
+
a
n
−
2
x
n
2
−
1
)
f
2
(
x
)
=
(
a
1
+
a
3
x
+
a
5
x
2
+
.
.
.
+
a
n
−
1
x
n
2
−
1
)
\begin{array}{c} f_1(x) = (a_0 + a_2x+a_4x^2+...+a_{n-2}x^{\frac{n}{2}-1}) \cr \newline f_2(x) = (a_1 + a_3x+a_5x^2+...+a_{n-1}x^{\frac{n}{2}-1}) \end{array}
f1(x)=(a0+a2x+a4x2+...+an−2x2n−1)f2(x)=(a1+a3x+a5x2+...+an−1x2n−1)
∴ f ( x ) = f 1 ( x 2 ) + x f 2 ( x 2 ) \therefore f(x) = f_1(x^2)+xf_2(x ^ 2) ∴f(x)=f1(x2)+xf2(x2)
再设
k
<
n
2
k < \dfrac{n}{2}
k<2n,把
w
n
k
w^k_n
wnk作为
x
x
x代入
f
(
x
)
f ( x )
f(x)(接下来几步变换要多想想单位根的性质)
f ( w n k ) = f 1 ( ( w n k ) 2 ) − w n k f 2 ( ( w n k ) 2 ) = f 1 ( w n 2 k ) − w n k f 2 ( w n 2 k ) = f 1 ( w n 2 k + w n k f 2 ( w n 2 k ) \begin{array}{c} f(w^k_n) \cr \newline = f_1((w^k_n)^2)-w^k_nf_2((w^k_n)^2) \cr \newline = f_1(w^{2k}_n)-w^k_nf_2(w^{2k}_n) \cr \newline =f_1(w^k_{\frac{n}{2}} + w^k_nf_2(w^k_{\frac{n}{2}}) \end{array} f(wnk)=f1((wnk)2)−wnkf2((wnk)2)=f1(wn2k)−wnkf2(wn2k)=f1(w2nk+wnkf2(w2nk)
那么对于
f
(
w
n
k
+
n
2
)
f(w_n^{k+\frac{n}{2}})
f(wnk+2n)的话,带入
w
n
k
+
n
2
w_n^{k+\frac{n}{2}}
wnk+2n
f
(
w
n
k
+
n
2
)
=
f
1
(
w
n
2
k
+
n
)
+
w
n
k
+
n
2
f
2
(
w
n
2
k
+
n
)
=
f
1
(
w
n
2
k
w
n
n
)
−
w
n
k
f
2
(
w
n
2
k
w
n
n
)
=
f
1
(
w
n
2
k
)
−
w
n
k
f
2
(
w
n
2
k
)
=
=
f
1
(
w
n
2
k
)
−
w
n
k
f
2
(
w
n
2
k
)
\begin{array}{c} f(w_n^{k+\frac{n}{2}}) \cr \newline =f_1(w_n^{2k+n}) + w_n^{k+\frac{n}{2}}f_2(w_n^{2k+n}) \cr \newline =f_1(w_n^{2k}w^n_n)-w_n^kf_2(w_n^{2k}w^n_n) \cr \newline =f_1(w_n^{2k}) - w_n^kf_2(w_n^{2k}) \cr \newline ==f_1(w_{\frac{n}{2}}^{k}) - w_n^kf_2(w_{\frac{n}{2}}^{k}) \end{array}
f(wnk+2n)=f1(wn2k+n)+wnk+2nf2(wn2k+n)=f1(wn2kwnn)−wnkf2(wn2kwnn)=f1(wn2k)−wnkf2(wn2k)==f1(w2nk)−wnkf2(w2nk)
- 你发现了什么
f ( w n k ) f(w^k_n) f(wnk)和 f ( w n k + n 2 ) f(w_n^{k+\frac{n}{2}}) f(wnk+2n)两个多项式后面只有符号不同
就是说,如果我们已经知道 f 1 ( w n k ) f_1{(w^k_n)} f1(wnk)和 f 2 ( w n k ) f_2{(w^k_n)} f2(wnk),我们就能同时知道 f ( w n k ) f(w^k_n) f(wnk)和 f ( w n k + n 2 ) f(w_n^{k+\frac{n}{2}}) f(wnk+2n)得知。所以,我们可以用递归实现。
FFT就是将系数表示法转化成点值表示法相乘,再由点值表示法转化为系数表示法的过程,第一个过程叫做求值(DFT),第二个过程叫做插值(IDFT)
插值只要将所有的
w
n
k
w^k_n
wnk变成
w
n
k
+
n
2
w^{k+\frac{n}{2}}_n
wnk+2n,就是将虚部取反,再将结果除以长度(即
n
n
n),至于为什么,我们可以这样考虑。
我们可以考虑把原来的要做的操作用矩阵的形式表现出来:
这是DFT,我们要求的IDFT,我们已知了左边和右边的两个矩阵,要求中间那个,就相当于是求最左边那个矩阵的逆,然后乘右边那个矩阵。它的逆就是
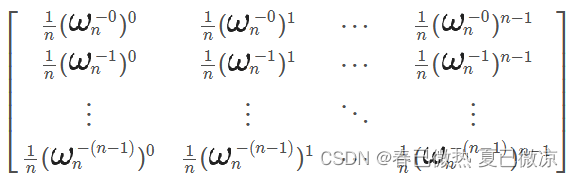
手算一下,发现(下面要
c
o
s
(
a
)
=
c
o
s
(
−
a
)
cos(a)=cos(-a)
cos(a)=cos(−a)和
s
i
n
(
−
a
)
=
−
s
i
n
(
a
)
sin(-a)=-sin(a)
sin(−a)=−sin(a))
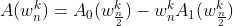
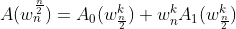
然后就可以了。
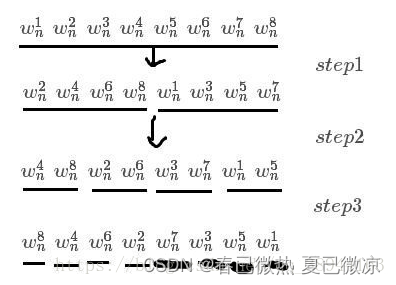
当我们做递归版的FFT的时候,在第i层就相当于把当前数的二进制第i位为零的分一类,为一的分一类,然后分别递归进去。
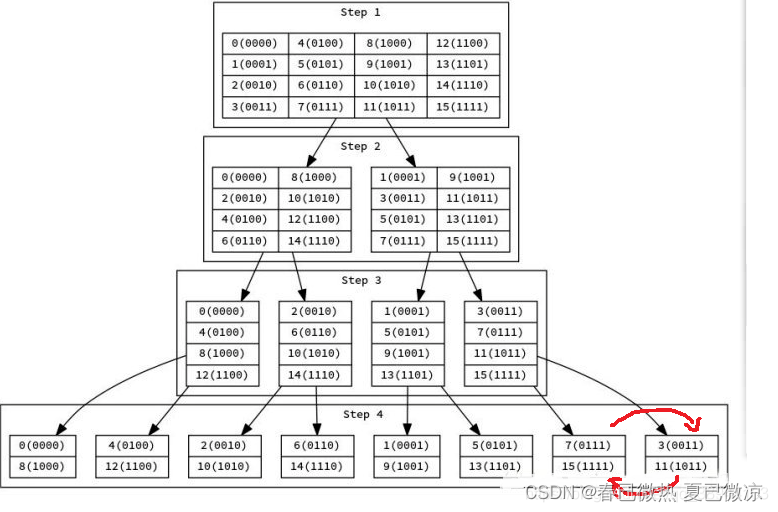
注意这副图的原图最后两个地方放反了
Last.蝴蝶变换

还是先看这张图
原序列:0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
位逆序置换后:0 8 4 12 2 10 6 14 1 9 5 13 3 11 7 15
然后我们发现了一个神奇的规律,把原序列和置换后的序列的对应位转换为二进制之后是刚好翻转过来的
如1的二进制是0001,8的二进制则是1000,2的二进制是0010,4的二进制是0100,其他也都是如此
然后按照置换后的一层一层往上合并就行了
位逆序置换可以用类似数位dp的方法求出来
卷积:
设
a
i
,
b
i
{a_i},{b_i}
ai,bi是两个数列,那么这两个数列的卷积
c
i
{c_i}
ci的定义为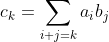
拿一个例子来看:
123
×
456
=
?
123 \times 456 = ?
123×456=?
不妨令:
f
(
x
)
=
1
×
x
2
+
2
×
x
+
3
=
{
1
,
2
,
3
}
f(x) = 1 \times x^2 + 2 \times x + 3 = \{1, 2, 3\}
f(x)=1×x2+2×x+3={1,2,3}
g ( x ) = 4 × x 2 + 5 × x + 6 = { 4 , 5 , 6 } g(x) = 4 \times x^2 + 5 \times x + 6 = \{4,5,6\} g(x)=4×x2+5×x+6={4,5,6}
f
(
10
)
×
g
(
10
)
=
{
4
,
13
,
28
,
27
,
15
}
f(10) \times g(10) = \{4,13,28,27,15\}
f(10)×g(10)={4,13,28,27,15},发现有一些大于等于
10
10
10.
我们只需想竖式一样将大于等于
10
10
10的数仅为,得到
f
(
2
)
×
g
(
2
)
=
{
5
,
6
,
0
,
8
,
8
}
f(2) \times g(2) = \{5,6,0,8,8\}
f(2)×g(2)={5,6,0,8,8}
∴ 123 × 456 = 56088 \therefore 123 \times 456 = 56088 ∴123×456=56088





















 1165
1165











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








