目录
fundamental dichotomy theorem for Julia sets
本文部分内容来自matrix67的博客 Matrix67.com - Home
一，常见分形
1，Julia集
用复变函数作为迭代方程，如果一个点在不断迭代之后是模值收敛的，那么就称之为收敛点。
所有收敛点组成的合集叫Julia集，每个不同的C对应的Julia集（如果存在的话）都不一样。
绘制Julia集的代码：
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
def genZ(axis, nx, ny):
x0, x1, y0, y1 = axis
x = np.linspace(x0, x1, nx)
y = np.linspace(y0, y1, ny)
real, img = np.meshgrid(x, y)
z = real + img * 1j
return z
# 用于生成Julia集
def getJulia(z, c, n, n0=0, m=2):
out = abs(z)
print(out)
for i in range(n0, n0 + n): #n是迭代次数
absz = abs(z)
z[absz > m] = 0
out[absz > m] = i
z = z * z + c
return out
n = 1000
axis = [-2, 2, -2, 2] # 规定矩形范围，即绘图范围
z = genZ(axis, n, n) # 生成axis范围内的n*n个点
c = 0.5-0.4j
mBrot = getJulia(z, c, 50)
plt.imshow(mBrot, cmap=cm.jet, extent=axis)
plt.show()c = 0.5-0.4j的结果： c = 0.75j的结果：
c = 0.998 + 0.401j的结果：
c = -0.75的结果：
c = 0.285的结果：
c = -0.8+0.156j的结果：
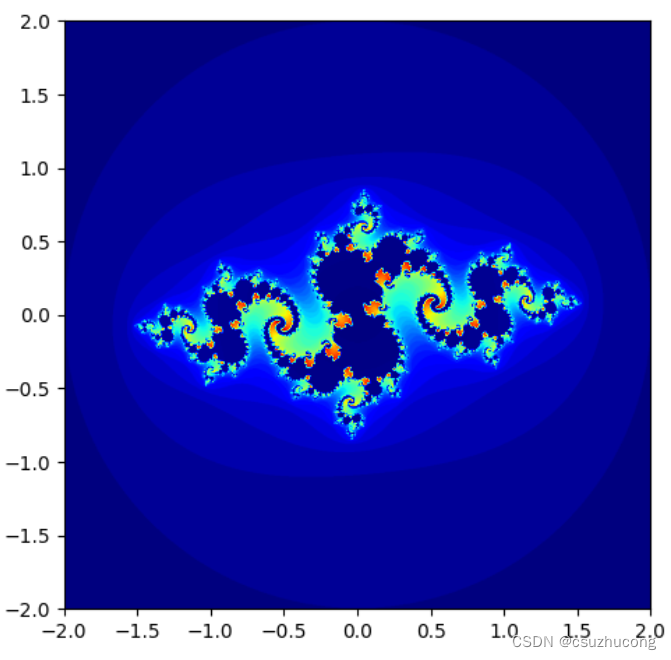
c = -0.835 -0.2321j 的结果：
c = -0.70176-0.3842j的结果：
fundamental dichotomy theorem for Julia sets
一个 Julia 集要么是完全连通的，任意两点间都有一条通路；要么是完全不连通的，整个图形全是一个个孤立的点。
参考：点击打开链接
总结：
即如果0是收敛点，那么就是完全连通的，否则就是完全不连通的。
这其实就得到曼德勃罗集的定义。
2，Mandelbrot（曼德勃罗）集
曼德勃罗集是使得迭代方程有收敛点的C的集合。
如果有收敛点，那么Z=0就是一个收敛点，经过一次迭代之后z=c
依据这个原理得到绘制代码：
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
def genZ(axis, nx, ny):
x0, x1, y0, y1 = axis
x = np.linspace(x0, x1, nx)
y = np.linspace(y0, y1, ny)
real, img = np.meshgrid(x, y)
z = real + img * 1j
return z
# 用于生成Julia集
def getJulia(z, c, n, n0=0, m=2):
out = abs(z)
print(out)
for i in range(n0, n0 + n): #n是迭代次数
absz = abs(z)
z[absz > m] = 0
out[absz > m] = i
z = z * z + c
return out
n = 1000
axis = [-2, 2, -2, 2] # 规定矩形范围，即绘图范围
z = genZ(axis, n, n) # 生成axis范围内的n*n个点
c = z
mBrot = getJulia(z, c, 50)
plt.imshow(mBrot, cmap=cm.jet, extent=axis)
plt.show()
Julia集和Mandelbrot集的关系
定义四元布尔函数g(x1,y1,x2,y2)：取起点为x1 + i y1，C=x2 + i y2，根据迭代方程 进行无限迭代，如果收敛则函数值为1，否则函数值为0
所有使得g=1的点构成的集合，就是四维Julia-Mandelbrot集合。
这个四维集合是唯一确定的一个集合，Julia集是它的二维切片，切的位置取决于C，Mandelbrot集也是它的切片，切的位置是x1=y1=0
更多资料：
https://www.skytopia.com/project/fractal/mandelbulb.html
https://christopherolah.wordpress.com/2011/08/08/the-real-3d-mandelbrot-set/
3，Koch（科赫）雪花
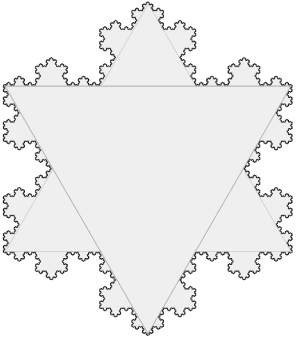
雪花是三个Koch曲线组成，严格来讲Koch曲线才是分形。
Koch曲线：
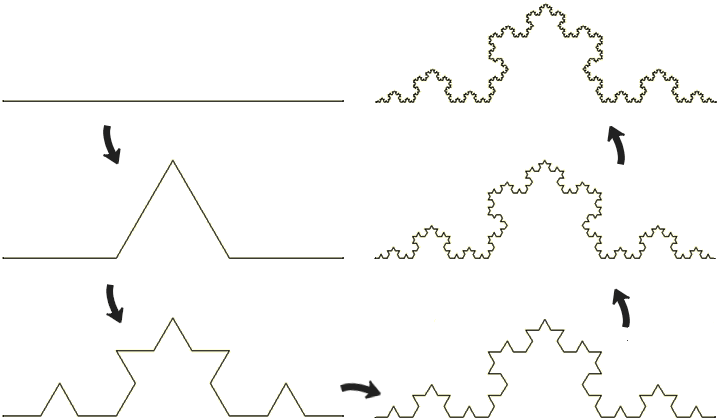
4，Hilbert（希尔伯特）曲线
用递归的方式铺满2^n * 2^n的方格，起点和终点是同一侧的2个角落格子。
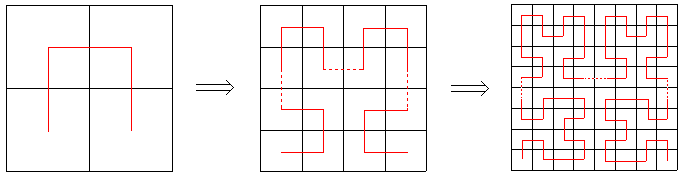
当n趋于正无穷就得到一条铺满整个正方形的连续曲线，叫Hilbert曲线，它的近似示例：
起点和终点是正方形同一侧的2个顶点。
三维Hilbert曲线：
OJ练习
5，Sierpinski（谢尔宾斯基）三角形
（1）等边三角形外形
Sierpinski三角形其实是一条曲线，内部面积为0。
（2）直角三角形外形
用DFS来构造的代码：
void dfs(Mat& img, int w, int h, int s)
{
if (s == 1) {
img.at<char>(w, h) = 1;
return;
}
dfs(img, w, h, s / 2);
dfs(img, w + s / 2, h, s / 2);
dfs(img, w, h + s / 2, s / 2);
}
int main()
{
int size = 512;
Mat img = Mat::zeros(size, size, CV_8U) + 255;
dfs(img, 0, 0, size);
imshow("img", img);
cv::waitKey(0);
return 0;
}
用位运算来构造的代码：
int main()
{
int size = 512;
Mat img = Mat::zeros(size, size, CV_8U) + 255;
for (int w = 0; w < size; w++) {
for (int h = 0; h < size; h++) {
if ((w | h) == size-1)img.at<char>(w, h) = 0;
}
}
imshow("img", img);
cv::waitKey(0);
return 0;
}
（3）任意三角形外形
Sierpinski三角形有一个神奇的性质：如果某一个位置上有点（没被挖去），那么它与原三角形顶点的连线上的中点处也有点。利用这个性质，也可以用于构造曲线，从起点开始，每次根据已有的点产生新的点，不断累积即可形成曲线。
int main()
{
int size = 512;
Mat img = Mat::zeros(size, size, CV_8U) + 255;
int w = 0, h = 0;
int ws[] = { 0,0,size };
int hs[] = { 0,size,0 };
for (int i = 0; i < 20000; i++) {
int r = rand() % 3;
w = (w + ws[r]) / 2;
h = (h + hs[r]) / 2;
img.at<char>(w, h) = 0;
}
imshow("img", img);
cv::waitKey(0);
return 0;
}
更神奇的是，其实无论从哪个点（理论上是整个平面内任意一点）开始迭代，得到的分形三角形都是一样的。
而且，只要修改顶点坐标，就能得到任意外形的分形三角形：
int ws[] = { 100,200,300 };
int hs[] = { 400,500,100 };
6，Sierpinski地毯
和Sierpinski三角形差不多。
void dfs(Mat& img, int r, int c, int s)
{
if (s == 1) return;
s /= 3;
for (int i = 0; i < 3; i++)for (int j = 0; j < 3; j++) {
int r2 = r + s * i, c2 = c + s * j;
if (i == 1 && j == 1) {
for(int r=r2;r<r2+s;r++)for(int c=c2;c<c2+s;c++)img.at<char>(r, c) = 1;
}
else dfs(img, r2, c2, s);
}
}
int main()
{
int size = 9*9*9;
Mat img = Mat::zeros(size, size, CV_8U) + 255;
dfs(img, 0, 0, size);
imshow("img", img);
cv::waitKey(0);
return 0;
}
二，其他分形
1，分形+镶嵌画
埃舍尔的画：圆形极限
2，三维图形
Menger海绵体，把Sierpinski地毯拓展到了三维
它的斜截面：
分形抽屉
3，Kögra分形字体
4，分形+不可能图形
Koch（科赫）雪花 + 彭罗斯三角
Sierpinski（谢尔宾斯基）三角形 + 彭罗斯三角
Cantor（康托）集 + 恶魔的音叉
Hilbert（希尔伯特）曲线 + 恶魔的音叉
勾股树 + 彭罗斯三角
5，迭代与分形
迭代和分形可以说是差不多对应的概念， 从某种意义上来说，分形其实就是不停地迭代，
只不过，分形的对象一般是经过无穷迭代之后趋于有限的一个现象，从视觉上来看，很有艺术性，从数学上来看，开辟了分数维度等新领域。
包括无穷皇后的构造，我觉得也是分形。
三，分形维数
1，分维
分形图形的复杂程度可以用分维（分形维数）来进行定量的描述。
随着分形理论的发展 ,现在已经有多种测定和计算分形维数的方法 ,有通过改变观察尺度、根据测度关系、根据相关函数、根据分布函数和频谱求维数这 5 类方法。
例如变步长法就属于通过改变观察尺度求维数的方法。
2，Hausdorff 维数
现在用得较多的Hausdorff（豪斯多夫）维数 ,其定义是 :
把一个 D维的几何对象的每一维放大L 倍 ,则该对象就会相应放大 ,若放大倍数为 K ,则三者有以下的关系 : L^D = K，即 D= In K / InL
理论上有无穷种分维。
如果一个自相似形包含自身N份，每一份的一维大小都是原来的1/s，则这个相似形的Hausdorff维度为log(N)/log(s)
一个Koch曲线包含四个小Koch曲线，大小两个Koch曲线的相似比为1/3，因此Koch曲线的Hausdorff维度为log(4)/log(3)=1.26
一个Hilbert曲线包含自身4份，每一份的一维大小都是原来的一半，因此维度等于log(4)/log(2)=2
3，变步长法
变步长法是用具有一定特征长度 r 的线段所构成的折线来近似地代替曲线 ,改变 r 的值 , 从而求出分维的方法。
从曲线上的任一点出发 ,以 其为圆心 ,适当的步长 r 为半径作圆 ,圆与曲线交于二 点;再以一交点为圆心 , r 为半径 ,沿曲线的一个方向 (顺时针或逆时针) 作圆 ,如此重复下去 ,直到交点与出 发点的距离小于 r 为止。这样就可以得到步长 r 和步 数 N ( r) (即圆的个数) 这一组数据。改变步长 r,如图 1 中的 a1到 a2 ,重复上述过程 ,即可得到若干组 r 和 N ( r) 的数据。
根据N(r)*r^D是常数，可以求出D
四，实际应用
1，分形虎钳
几乎可以把任意形状的物体给紧紧的夹住。
五，待更新
分形几何 https://zhuanlan.zhihu.com/p/107069796
分形相关puzzle 如分形芯片
3001
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
