目录
一,内固、外固
在一个图中可以选出一组点,使得其余的点至少与这组点中某一个点相邻,选出的这组点称为图的一个外固集,外固集中所含点数的最小值称为外固数。
在一个图中可以选出一组点,使得任意两点都不相邻,选出的这组点称为图的一个内固集,内固集中所含点数的最大值称为内固数。
内固和外固的关系
显然,内固数 ≥ 外固数
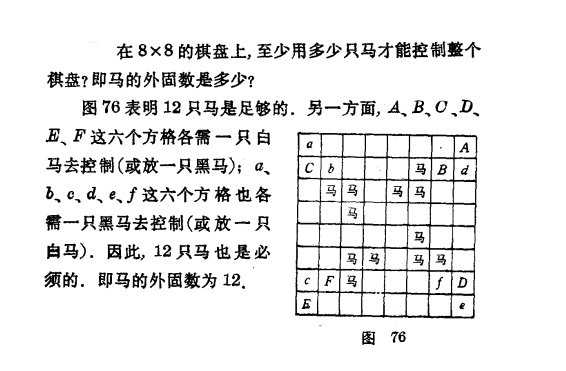
已经被证明,N>3时N皇后问题有解,所以它的内固数等于外固数。
马的內固数是(n*n+1)/2,而外固数则复杂一些,8*8的棋盘中外固数是12,内固数是32。
最大内固集(即内固数对应的内固集)一定也是个外固集,反之,最小外固集却不一定是内固集。
是否存在一个图,存在它的一个内固集也是外固集,其中所含点数既不是内固数也不是外固数?
感觉应该是存在的。
二,马的内固问题
n*n的棋盘上(n>4)最多可以放多少个马,使得它们互不攻击,即马的内固数是多少。
如果n=2*k,因为有一个哈密顿圈,圈的大小是4*k*k,所以内固数不超过2*k*k,即n*n/2。
如果n=2*k+1,因为有一个哈密顿链,圈的大小是4*k*k+4*k+1,所以内固数不超过2*k*k+2*k+1,即(n*n+1)/2。
我们将棋盘按照国际象棋的棋盘来染色,使得白色的格子数-黑色的格子数=0或1。
也就是说,白色格子有(n*n+1)/2个,在所有的白色格子里面放马,这些马都不能互相攻击。
所以,马的內固数是(n*n+1)/2
三,马的外固问题
对于8*8的棋盘,求马的外固数和外固集
所以外固数自然是12了,那么外固集有哪些呢?
我的解法:(下面所有的内容都是自己想的,后来才看到书上这一页)
初始代码是用24层的循环进行找答案试试,虽然要运行结束不太现实,但是如果运气好,循环只进行一部分就得到一部分答案,也不是不可能。
<iostream>
using namespace std;
void exist(int list[][8], int i, int j) //将可以到达的8个(或少于8个)格子记录下“已经覆盖”
{
if (i > -1 && i<8 && j>-1 && j < 8)list[i][j] = 1;
}
void place_a_horse(int list[][8], int i, int j) //更新已经覆盖的格子的信息
{
list[i][j] = 1;
exist(list, i - 2, j - 1);
exist(list, i - 2, j + 1);
exist(list, i - 1, j - 2);
exist(list, i - 1, j + 2);
exist(list, i + 2, j + 1);
exist(list, i + 2, j - 1);
exist(list, i + 1, j + 2);
exist(list, i + 1, j - 2);
}
void action(int list[][8], int i1, int j1, int i2, int j2, int i3, int j3, int i4, int j4, int i5, int j5, int i6, int j6, int i7, int j7, int i8, int j8, int i9, int j9, int ia, int ja, int ib, int jb, int ic, int jc)
{
for (int i = 0; i < 8; i++)for (int j = 0; j < 8; j++)list[i][j] = 0;
place_a_horse(list, i1, j1); //放入12个棋子
place_a_horse(list, i2, j2);
place_a_horse(list, i3, j3);
place_a_horse(list, i4, j4);
place_a_horse(list, i5, j5);
place_a_horse(list, i6, j6);
place_a_horse(list, i7, j7);
place_a_horse(list, i8, j8);
place_a_horse(list, i9, j9);
place_a_horse(list, ia, ja);
place_a_horse(list, ib, jb);
place_a_horse(list, ic, jc);
for (int i = 0; i < 8; i++)for (int j = 0; j < 8; j++)if (list[i][j] == 0)return;
cout << i1 << j1 << i2 << j2 << i3 << j3 << " " << i4 << j4 << i5 << j5 << i6 << j6 << " ";
cout << i7 << j7 << i8 << j8 << i9 << j9 << " " << ia << ja << ib << jb << ic << jc << endl;
cout << list[2][0] << endl;
}
//12个棋子从上往下遍历循环
void visit12(int list[][8])
{
for (int i1 = 0; i1 < 3; i1++) for (int j1 = 0; j1 < 8; j1++)
for (int i2 = i1; i2 < 3; i2++) for (int j2 = 0; j2 < 8; j2++)
for (int i3 = i2; i3 < 3; i3++) for (int j3 = 0; j3 < 8; j3++)
for (int i4 = i3; i4 < 3; i4++) for (int j4 = 0; j4 < 8; j4++)
for (int i5 = i4; i5 < 8; i5++) for (int j5 = 0; j5 < 8; j5++)
for (int i6 = i5; i6 < 8; i6++) for (int j6 = 0; j6 < 8; j6++)
for (int i7 = i6; i7 < 8; i7++) for (int j7 = 0; j7 < 8; j7++)
for (int i8 = i7; i8 < 8; i8++) for (int j8 = 0; j8 < 8; j8++)
for (int i9 = 5; i9 < 8; i9++) for (int j9 = 0; j9 < 8; j9++)
for (int ia = 5; ia < 8; ia++) for (int ja = 0; ja < 8; ja++)
for (int ib = 5; ib < 8; ib++) for (int jb = 0; jb < 8; jb++)
for (int ic = 5; ic < 8; ic++) for (int jc = 0; jc < 8; jc++)
action(list, i1, j1, i2, j2, i3, j3, i4, j4, i5, j5, i6, j6, i7, j7, i8, j8, i9, j9, ia, ja, ib, jb, ic, jc);
}
int main()
{
int list[8][8];
visit12(list);
cout << "end";
system("pause>nul");
return 0;
}结果运气并不好,得不到答案。
于是我决定尝试先找找有没有非常规则的答案。
第一种,上下对称且左右对称
visit3(int list[][8]) //只对左上角的3个进行遍历循环
{
for (int i1 = 0; i1 < 3; i1++) for (int j1 = 0; j1 < 4; j1++)
for (int i2 = i1; i2 < 4; i2++) for (int j2 = 0; j2 < 4; j2++)
for (int i3 = i2; i3 < 4; i3++) for (int j3 = 0; j3 < 4; j3++)
action(list, i1, j1, i2, j2, i3, j3, 7 - i1, j1, 7 - i2, j2, 7 - i3, j3, i1, 7 - j1, i2, 7 - j2, i3, 7 - j3, 7 - i1, 7 - j1, 7 - i2, 7 - j2, 7 - i3, 7 - j3);//上下对称,左右对称
}用visit3代替visit12
可惜,并没有这样的答案。
第二种,上下对称
visit6(int list[][8])
{
for (int i1 = 0; i1 < 3; i1++) for (int j1 = 0; j1 < 8; j1++)
for (int i2 = i1; i2 < 3; i2++) for (int j2 = 0; j2 < 8; j2++)
for (int i3 = i2; i3 < 3; i3++) for (int j3 = 0; j3 < 8; j3++)
for (int i4 = i3; i4 < 3; i4++) for (int j4 = 0; j4 < 8; j4++)
for (int i5 = i4; i5 < 8; i5++) for (int j5 = 0; j5 < 8; j5++)
for (int i6 = i5; i6 < 8; i6++) for (int j6 = 0; j6 < 8; j6++)
action(list, i1, j1, i2, j2, i3, j3, i4, j4, i5, j5, i6, j6,7-i1,j1,7-i2,j2,7-i3,j3,7-i4,j4,7-i5,j5,7-i6,j6); //上下对称
}可惜,并没有这样的答案。
第三种,90°旋转对称
这时我发现,2个马无法控制左上角的2*2的正方形,为了控制左上角的4个格子,左上角的16个格子里面一定至少有3个马。恰好一共12个马,所以每个4*4的角落必定是恰好3个马。
于是我考虑左上角的4*4=16个格子里面,怎么样放置3个马才能覆盖左上角的4个格子
将visit3里面改成如下代码
for (int i1 = 0; i1 < 3; i1++) for (int j1 = 0; j1 < 4; j1++)
for (int i2 = i1; i2 < 4; i2++) for (int j2 = 0; j2 < 4; j2++)
for (int i3 = i2; i3 < 4; i3++) for (int j3 = 0; j3 < 4; j3++)
{
for (int i = 0; i < 8; i++)for (int j = 0; j < 8; j++)list[i][j] = 0;
place_a_horse(list, i1, j1);
place_a_horse(list, i2, j2);
place_a_horse(list, i3, j3);
if (list[0][0] && list[0][1] && list[1][0] && list[1][1])
cout << i1 << j1 << i2 << j2 << i3 << j3 <<" ";
}运行结果是
000322 001122 002223 002230 002232 002322 030022 031222 032122 032221 111222 112122 112221 121122 122223 122230 122232 122322 212223 212230 212232 212322 222123 222130 222132 222321 232122 232221 end
终于,这次运气还不错,一举发现了答案。
然后我根据上面的输出进行了排查,发现分4块循环对称的只有这1种方案(另外一种方案无非是翻转过来使得风车的方向反过来而已)。
至于除了这三种情况,有没有其他形式的答案就不清楚了。
四,八皇后问题
著名的8皇后问题就是,求出8*8有多少个不同的內固集。
8皇后的内固集有92种,即8皇后问题有92种不同的摆法。

在 75象棋(6)这篇文章中我给出了一个非常对称的解。
五,N皇后问题
下面讨论一般的N皇后问题。
N*N的棋盘上放N个皇后的方法数是int list[10] = { 1, 0, 0, 2, 10, 4, 40, 92, 352, 724 };
当N=2或3时,內固数是N-1而不是N,所以list为0
我们猜想当N>3时list不为0,即内固数为N
书上说这个结论是对的,不过我没找到证明。
HDU 2553 N皇后问题
题目:
Description
在N*N的方格棋盘放置了N个皇后,使得它们不相互攻击(即任意2个皇后不允许处在同一排,同一列,也不允许处在与棋盘边框成45角的斜线上。
你的任务是,对于给定的N,求出有多少种合法的放置方法。
Input
共有若干行,每行一个正整数N≤10,表示棋盘和皇后的数量;如果N=0,表示结束。
Output
共有若干行,每行一个正整数,表示对应输入行的皇后的不同放置数量。
Sample Input
1 8 5 0
Sample Output
1 92 10
这个题目的思路倒是不难,就是典型的深度优先搜索。
但是结果超时了,题目也没说测试数据有多少,估计是不少。
因为N不超过10,所以干脆把结果硬编码了。
代码:
#include<iostream>
using namespace std;
int main()
{
int n;
int list[10] = { 1, 0, 0, 2, 10, 4, 40, 92, 352, 724 };
while (cin >> n)
{
if (n == 0)break;
cout << list[n-1] << endl;
}
return 0;
}力扣 51. N皇后
题目:
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例:
输入: 4
输出: [
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。
代码:
int m;
int list_[100];
vector<vector<string>>ans;
void place(int row)
{
if (row == m){
string s;
vector<string>res;
for (int j = 0; j < m; j++){
s = "";
for (int i = 0; i < list_[j]; i++)s.append(".");
s.append("Q");
for (int i = list_[j]+1; i < m; i++)s.append(".");
res.insert(res.end(), s);
}
ans.insert(ans.end(), res);
return;
}
for (int i = 0; i < m; i++)
{
bool flag = true;
for (int j = 0; j < row; j++){
if (list_[j] == i || list_[j] - j == i - row || list_[j] + j == i + row){
flag = false;
}
}
if (flag)
{
list_[row] = i;
place(row + 1);
}
}
}
class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
ans.clear();
if (n <= 0)return ans;
m = n;
place(0);
return ans;
}
};力扣 52. N皇后 II
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
示例:
输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
代码:
int m, sum;
int list_[100];
void place(int row)
{
if (row == m)sum++;
for (int i = 0; i < m; i++)
{
bool flag = true;
for (int j = 0; j < row; j++)
if (list_[j] == i || list_[j] - j == i - row || list_[j] + j == i + row)flag = false;
if (flag)
{
list_[row] = i;
place(row + 1);
}
}
}
class Solution {
public:
int totalNQueens(int n) {
m = n;
sum = 0;
place(0);
return sum;
}
};六,无穷皇后问题
1,无穷皇后问题
在整个第一象限,每一行放一个皇后,每一列放一个皇后,使得所有皇后不能互相攻击,怎么放呢?
在《proofs without words》一书中给出了迭代式的答案:

2,迭代法的正确性
最小的N皇后是N=4

迭代一次变成:

第4行的皇后和第9行的皇后在一条斜线上,所以这样迭代是不行的。
不难发现,这样的迭代正确与否,取决于2个N皇后挨着放在一起,会不会有在同一条斜线上的(包括左斜线和右斜线)
(上下挨着放和左右挨着放是等价的,只需要看一个即可)
上述N=4时的构造,2个放一起时变成:有斜线上不止一个皇后
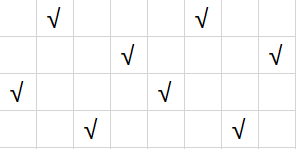
而上述N=5的构造,2个放一起时,没有在一条斜线上的
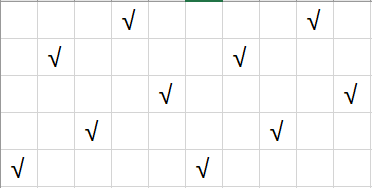
为了方便,我把这称为严格N皇后问题。
3,严格N皇后
N皇后问题的解中,有哪些满足,两个N*N的表格左右相邻拼接起来之后,仍然没有任何2个皇后在一条直线上?
首先编程算一下小数据,看看规律。
代码:
#include<iostream>
using namespace std;
#define NORZERO(x) x==0||x==n||x==-n
int n, sum;
int list[30];
void place(int row)
{
if (row == n)sum++;
bool flag;
for (int i = 0; i < n; i++)
{
flag = true;
for (int j = 0; flag && j < row; j++)
if (list[j] == i || NORZERO(list[j] - j - i + row) || NORZERO(list[j] + j - i - row))flag = false;
if (flag)
{
list[row] = i;
place(row + 1);
}
}
}
int main()
{
for (n = 4;;n++)
{
sum = 0;
place(0);
cout << "n=" << n << ",ans=" << sum << endl;
}
return 0;
}输出:
n=4,ans=0
n=5,ans=10
n=6,ans=0
n=7,ans=28
n=8,ans=0
n=9,ans=0
n=10,ans=0
n=11,ans=88
n=12,ans=0
n=13,ans=4524
n=14,ans=0
n=15,ans=0
n=16,ans=0
n=17,ans=140692
n=18,ans=0
多么令人激动的结果!貌似只有n是质数的时候有解,而且解的个数是n的倍数!
为了获得更多数据,我不得不优化程序。
优化思路:
递归的时候记录哪些竖线、左斜线、右斜线被占了,回溯的时候还原。这样判断一个位置能不能放皇后的时候就可以直接算出来。
优化代码:
#include<iostream>
using namespace std;
#define simple1(x) x<0?x+n:x
#define simple2(x) x>=n?x-n:x
int n, sum;
const int M = 30;
int line[M], lineleft[M], lineright[M];
void place(int row)
{
if (row == n)sum++;
for (int i = 0; i < n; i++)
{
if (line[i] || lineleft[simple1(i - row)] || lineright[simple2(i + row)])continue;
line[i] = lineleft[simple1(i - row)] = lineright[simple2(i + row)] = 1;
place(row + 1);
line[i] = lineleft[simple1(i - row)] = lineright[simple2(i + row)] = 0;
}
}
int main()
{
for (n = 4;;n++)
{
sum = 0;
memset(line, 0, sizeof(line));
memset(lineleft, 0, sizeof(lineleft));
memset(lineright, 0, sizeof(lineright));
place(0);
cout << "n=" << n << ",ans=" << sum << endl;
}
return 0;
}算法有明显的提升,不过到n=19的时候还是有点吃力。
只比上一个算法多算出来一个 n=19,ans=820496,不过这也进一步印证了上面的规律。
继续优化:不用数组记录,用状态压缩,从而实现快速枚举
优化代码:
#include<iostream>
using namespace std;
#define mi (1<<(n-1)) //最高位
#define turnr(x) (((x&1)?mi:0)+(x>>1)) //循环右移
#define turnl(x) ((x&mi)?((x^mi)<<1)|1:(x<<1)) //循环左移
int n, sum;
int line, lineleft, lineright;
void place(int row)
{
if (row == n)sum++;
lineleft = turnr(lineleft), lineright = turnl(lineright);
int lowbit,leave = ((1 << n) - 1) ^ (line | lineleft | lineright);
while (leave)
{
lowbit = leave & -leave;
line ^= lowbit, lineleft ^= lowbit, lineright ^= lowbit;
place(row + 1);
line ^= lowbit, lineleft ^= lowbit, lineright ^= lowbit;
leave ^= lowbit;
}
lineleft = turnl(lineleft), lineright = turnr(lineright);
}
int main()
{
for (n = 4;;n++)
{
sum = line = lineleft = lineright = 0;
place(0);
cout << "n=" << n << ",ans=" << sum << endl;
}
return 0;
}算法有了进一步提升,不过到了n=19之后仍然吃力,这时,我突然想明白了为什么所有的ans都是n的倍数,
因为对于轮换对称性!
第一行的皇后在每一列的情况下,解的数量都是一样的,如此,程序就可以进一步优化。
优化代码:
#include<iostream>
using namespace std;
#define mi (1<<(n-1)) //最高位
#define turnr(x) (((x&1)?mi:0)|(x>>1)) //循环右移
#define turnl(x) ((x&mi)?((x^mi)<<1)|1:(x<<1)) //循环左移
int n, sum;
int line, lineleft, lineright;
void place(int row)
{
if (row == n)sum++;
lineleft = turnr(lineleft), lineright = turnl(lineright);
int lowbit,leave = ((1 << n) - 1) ^ (line | lineleft | lineright);
while (leave)
{
lowbit = leave & -leave;
line ^= lowbit, lineleft ^= lowbit, lineright ^= lowbit;
place(row + 1);
line ^= lowbit, lineleft ^= lowbit, lineright ^= lowbit;
leave ^= lowbit;
}
lineleft = turnl(lineleft), lineright = turnr(lineright);
}
int main()
{
for (n = 4;;n++)
{
sum = 0;
line = lineleft = lineright = 1;
place(1);
cout << "n=" << n << ",ans=" << n* sum << endl;
}
return 0;
}输出:
n=4,ans=0
n=5,ans=10
n=6,ans=0
n=7,ans=28
n=8,ans=0
n=9,ans=0
n=10,ans=0
n=11,ans=88
n=12,ans=0
n=13,ans=4524
n=14,ans=0
n=15,ans=0
n=16,ans=0
n=17,ans=140692
n=18,ans=0
n=19,ans=820496
n=20,ans=0
n=21,ans=0
4,严格N皇后问题的轮胎模型
一个N*N的表格,如果左右相接,上下相接,就变成了一个轮胎。
严格N皇后问题可以表述为:在一个N*N的轮胎上放N个皇后,使得每行每列每斜线上都只有一个皇后。
这样,就很容易去思考对称性了。
行有轮换对称性,列有轮换对称性,关于两条对角线还有对称性。
因为每个解肯定是不会关于对角线对称的,所以把一个解沿着对角线翻转就会变成另外一个解。
5,严格N皇后问题和幻方
幻方构造法幻方构造法_nameofcsdn的博客-CSDN博客
这里的轮胎模型和本文的轮胎模型是一样的,其中轮换叠加构造法所用到的方阵,和本文的严格N皇后问题的解的构造,也有着千丝万缕的关系。
进一步的内容我就不探究了,因为工作比较忙,所以当初只写了这一节的标题就暂停了,过了许久之后再回忆起来,已经丢失了那一瞬间的灵感了,实在是可惜了。
七,皇后的外固问题
1,6*6
对于6*6的棋盘,皇后的外固数是3.
一方面,3个皇后是足够的:
参考 46象棋(4)
另一方面,2个皇后显然是不够的。
所以,对于6*6的棋盘,皇后的外固数为3
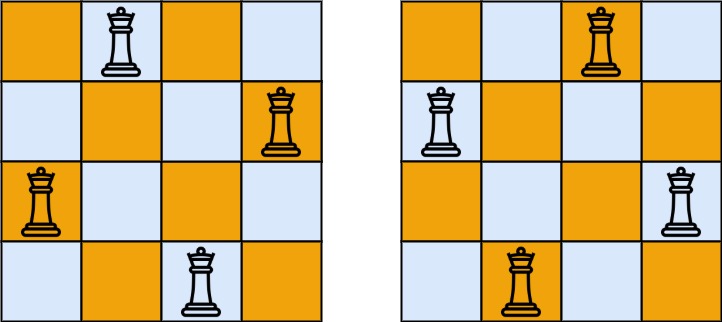
2,8*8
对于8*8的棋盘,皇后外固数是多少呢?
首先,5个皇后是可以控制棋盘的。
在 141象棋(11) 里面,还有一个更对称的外固集
其次,4个皇后是不行的。
所以,外固数为5

























 3602
3602











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








