拓扑图论、常见的图

目录

一，拓扑图论

二，彼得森图

三，正则图

四，完全图

1，完全图

2，K7

3，K5

五，二分图、完全二分图

六，多部图、完全多部图

七，平衡多部图、平衡完全多部图

八，广义子图、禁图表征

1，广义子图

2，广义子图定理

3，禁图表征

4，广义子图的二元关系

九，平面图

1，瓦格纳定理

十，竞赛图

---

一，拓扑图论

拓扑图论研究曲面中的图嵌入、图的空间嵌入及作为拓扑空间的图，还研究图的浸入。

二，彼得森图

彼得森图由10个点组成，它不是平面图。

三，正则图

每个节点的度数都是k的无向图，称为k-正则图。

对于有向图，这个度数指的是入度和出度之和。

所以对于奇数k，k-正则图一定包含偶数个顶点。

判断算法：

	//判断是不是k-正则图
	static bool isCompleteGraph(int k, UndirectedGraphData<int> &g)
	{
		for (auto &mi : g.adjaList) {
			if (mi.second.size() != k)return false;
		}
		return true;
	}

四，完全图

1，完全图

完全图指的是，对于不同的2点，点A到点B之间恰好有一条边，这样的简单图称为完全图。

n个点的无向完全图有n(n-1)/2条边，n个点的有向完全图有n(n-1)条边。

完全图用Kn表示。

无向完全图Kn是(n-1)正则图，有向完全图Kn是(2n-2)正则图。

2，K7

比如无向完全图K7是6正则图：

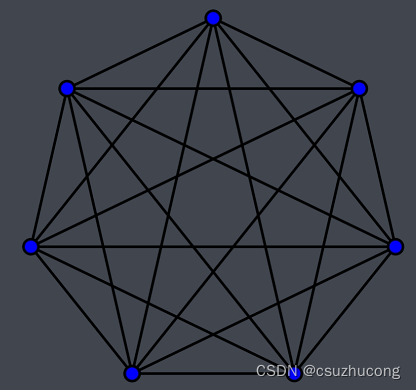
PS：正则图、完全图很适合用来做动漫特效，比如K7就可以表示集齐七龙珠之后，阵法中的能量交换路径。

3，K5

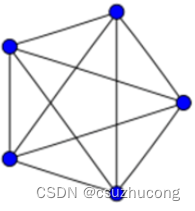
K5是彼得森图的广义子图。

五，二分图、完全二分图

二分图

六，多部图、完全多部图

若一个图的节点集能分成k个两两不交的非空子集，使得这个图的每一条边的两端点不在同一个子集内，则称这个图为k部图。

二部图也叫二分图。

完全k部图是一种特殊的k部图，可以把图中的顶点分成k个集合，使得任意2个集合各任取一个顶点都相连。

七，平衡多部图、平衡完全多部图

如果一个多部图中，任意2个子集的点数差都不超过1，则称为平衡多部图。

如果一个完全多部图是平衡多部图，则称为平衡完全多部图。

当k=2时，分别称为平衡二部图、平衡完全二部图。

八，广义子图、禁图表征

1，广义子图

参考图论

广义子图也叫图子式。

2，广义子图定理

待更新

https://zh.wikipedia.org/wiki/%E5%9B%BE%E5%AD%90%E5%BC%8F

3，禁图表征

禁图表征是一种图论专有的语法，该语法的形式是：

只有一个图不以某些图作为广义子图，那么这个图就满足某个性质。

这种定理，称为这种性质的禁图表征。

4，广义子图的二元关系

待更新

九，平面图

1，瓦格纳定理

瓦格纳定理就是平面图的禁图表征：

当且仅当一个图不存在完全图K5和完全二分图K3,3的子式时，这个图才是平面图。

十，竞赛图

竞赛图是通过在无向完全图中为每个边缘分配方向而获得的有向图。

竞赛图往往用来表达单循环赛事的胜负情况。