数学危机、经典悖论

在某个城市中有一位理发师，他的广告词是这样写的：“本人的理发技艺十分高超，誉满全城。我将为本城所有不给自己刮脸的人刮脸，我也只给这些人刮脸。我对各位表示热诚欢迎！”来找他刮脸的人络绎不绝，自然都是那些不给自己刮脸的人。可是，有一天，这位理发师从镜子里看见自己的胡子长了，他本能地抓起了剃刀，你们看他能不能给他自己刮脸呢？如果他不给自己刮脸，他就属于“不给自己刮脸的人”，他就要给自己刮脸，而如果他给自己刮脸呢？他又属于“给自己刮脸的人”，他就不该给自己刮脸。

3，罗素悖论

由所有不包含自身的集合所组成的集合，这个集合是否包含自身呢？

罗素悖论和理发师悖论是等价的。

罗素发现这个悖论是由集合包含自身所导致的，如果去掉这种自我指涉，就没有悖论了。

公理化集合论的建立，成功排除了集合论中出现的悖论，解决了第三次数学危机。

四，其他二难悖论

1，祖父悖论

假设你回到过去，在自己父亲出生前把自己的祖父母杀死；因为你祖父母死了，就不会有你的父亲；没有了你的父亲，你就不会出生；你没出生，你就不会将祖父母杀死，从而形成悖论。

下面这个台球虫洞悖论，本质和祖父悖论一样，都是因果悖论，但是做了极大的简化。

2，培里悖论

培里是英国的图书馆管理员。有一天他告诉罗素下面的悖论：英语中只有有限多个音节，只有有限多英语表达式包含少于40个音节，所以，用少于40个音节的表达式表示的正数数目只有有限多个。假设R为“不能由少于40个音的英语表达式来表示的最小正整数”(The least positive integer which is not denotedby an expression in the English language containing fewer than forty syllables)。但是，这段英语只包含三十几个音节，肯定比40个少，而且表示R，这自然产生了矛盾。

我的浅见：

假设R为“不能由少于40个音的英语表达式来表示的最小正整数”这一步是错的，因为用文字来描述一个数只是一种简单的映射，并没有规矩，只要我开心，我照样可以用“不能由少于40个音的英语表达式来表示的最小正整数”这个词首先直接用来表示1，虽然这样的描述让人很难理解，但是逻辑上并没有错误。

那么，在遇到了一个足够大的数之后，我们再想用“不能由少于40个音的英语表达式来表示的最小正整数”这个短语来表示就不行了，因为已经被用过了。

即使我们按照正常逻辑，1就是one，2就是two，也一定会遇到一个，除了“不能由少于40个音的英语表达式来表示的最小正整数”这个词之外，再也没有其他少于40个音节的词可以表示的数，如果此时我们用这个词来表示它，后面就一定还会遇到一个无法用任何少于40音节的词表示的数，因为这个词已经用过了。

3，格瑞林-纳尔逊悖论

如果一个形容词所表示的性质适用于这个形容词本身，比如“黑的”两字的确是黑的，那么这个形容词称为自适用的。反之，一个形容词如果不具有自适用的性质，就叫做非自适用的。在英语中：“Polysyllabic”(多音节的)，“English”(英语的)这些词都是自适用的形容词，而 “monosyllabic”(单音节的)、“French”(法语的)这些词就是非自适用的。我们来考虑“非自适用的”这个形容词，它是自适用的还是非自适用的呢？如果“非自适用的”是非自适用的，那么它就是自适用的；如果“非自适用的”是自适用的，那么按照这词的意思，则它是非自适用的，这就导出矛盾。

格瑞林-纳尔逊悖论的本质，其实就是说谎者悖论。

4，全能上帝悖论

（1）上帝能创造出一块他搬不动的石头吗？

如果我们说上帝是万能的，就会存在悖论：上帝能创造出一块他搬不动的石头吗？（如果我们说上帝不存在或者上帝不是万能的，那就没有悖论了）

这个悖论有点像说谎者悖论，但是深究起来不太一样。

首先，上帝是万能的，所以无论哪个石头，上帝都可以搬得动，也就是说，上帝搬不动的石头是不存在的。

然后，上述悖论就会变成，上帝能创造出一个不存在的物体吗？

一般来说，上帝能创造出目前不存在的物体，比如假设目前不存在电荷数为3.1415926的电子，但是明天说不定就存在了呢？反正你都相信上帝存在且万能了。

对于永远不存在的物体，上帝是创造不出来的。（这感觉又扯到因果律了）

但是，我仍然可以说上帝是万能的，因为万能指的是所有事情都能搞定，而不是所有形如“上帝能...”的命题都成立。

（2）上帝能证明上帝不是万能的吗？

如果我们说上帝是万能的，就会存在悖论：上帝能证明上帝不是万能的吗？

这就更接近说谎者悖论了。

首先，我还是相信上帝是万能的，所以“上帝不是万能的”就是个假命题。

然后，上述悖论就会变成，上帝能证明一个假命题是真命题吗？

不能，但是我还是认为上帝是万能的。和上一种情况类似，如果我说所有的证明其实都是在键盘上敲出一个满足条件的字符串，那么，对于任何条件，上帝要么告诉你不存在满足条件的字符串，要么可以敲出一个满足条件的字符串，但是上帝敲不出一个不存在的字符串。

结论是，上帝敲不出一个不存在的字符串，但是上帝仍然是万能的。

PS：考虑到哥德尔不完备性定理，把证明描述成敲出一个字符串并不恰当，但是这不是重点，如果要严谨一点只需要对上述论述稍作修改即可。

5，鳄鱼悖论

古希腊流传的故事，有一天，一条鳄鱼从一位母亲的手中抢走了她的孩子。这位母亲苦苦地哀求鳄鱼：“我只有这么一个孩子，求求你千万不要伤害他，你提出什么条件我都答应你。” 鳄鱼听了非常得意，就对这位母亲说：“那好，我向你提一个问题，让你猜，如果你答对了，我就不伤害你的孩子，并把孩子还给你；如果你答错了，我就要吃掉你的孩子。”

鳄鱼问这位母亲：你猜我会不会吃掉你的孩子？

这位聪明的母亲仔细地琢磨了片刻，说：“鳄鱼先生，我想你是要吃掉我的孩子的。”

那，鳄鱼到底要不要吃掉孩子呢？这就形成了悖论。

6，不死之酒

东方朔偷饮了汉武帝求得的据说饮了能够不死的酒，汉武帝要杀他，他说：“如果这酒真能使人不死，那么你就杀不死我；如果这酒不能使人不死（你能杀得死我），那么它就没有什么用处，不必杀我。”

7，半费之讼

普罗泰戈拉收了一名学生叫欧提勒士。普氏与他签订了这样一份合同：前者向后者传授辩论技巧，教他帮人打官司；后者入学时交一半学费，另一半学费则在他毕业后帮人打官司赢了之后再交。时光荏苒，欧氏从普氏那里毕业了。但他总不帮人打官司，普氏于是就总得不到那另一半学费。普氏为了要那另一半学费，他去与欧氏打官司。普氏认为无论官司输赢，他都应该拿到另一半学费，普氏却认为，无论官司输赢，他都不应该支付另一半学费。

五，来自日常生活的悖论

1，投票悖论（孔多塞悖论）

假设甲乙丙三人，面对ABC三个备选方案，有如下的偏好排序：

甲A>B>C

乙B>C>A

丙C>A>B

那么就会产生一个结果，大部分人都认为A>B，大部分人都认为B>C，大部分人都认为C>A，从而形成悖论。

类似的，Matrix67的博客中给出了稍复杂的一个例子：

有四颗骰子，分别用A、B、C、D来表示：

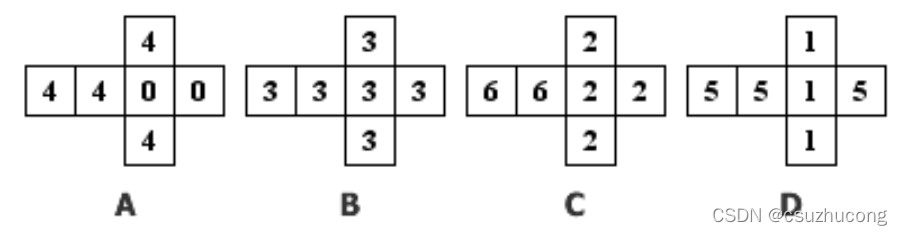
比较2个骰子的优劣，可以描述成，2个骰子pk时哪个胜率更高，

在这四颗骰子中，A赢B的概率是2/3，B赢C的概率是2/3，C赢D的概率是2/3，D赢A的概率还是2/3

2，特修斯之船悖论

如果特修斯的船上的木头被逐渐替换，直到所有的木头都不是原来的木头，那这艘船还是原来的那艘船吗？

我们认定同一性——认定一个事物是不是它本身的依据不是组成这一事物的元素，而是这一事物的内部结构——元素之间的关系，以及这一事物的时空连续性。

3，抽彩悖论

我合理地相信在一百万张彩票中有一张将中彩。但我并不合理地相信1号票将中彩，也没有理由相信2号票将中彩。这一过程可以继续下去，以至最终也没有理由相信任何单独一张票将中彩。于是悖论出现了，因为我确实相信有一张票将中彩。

如果换成连续性概率问题，可能更有悖论的感觉。

学过概率论的都知道，不可能事件的概率为0，但概率为0的不一定是不可能事件。

最简单的比如在线段上随机选一个点，任何一个点都有可能被选中，但被选中的概率都是0

4，公交车悖论（等待时间悖论）

公交车悖论：当你等平均10分钟一班的公交时，理论上你所需等待的平均时间是5分钟，但你总感觉等的时间总比5分钟要长。

抛开“人总是记住悲剧而不是喜剧”这类的心理因素，我们看一下客观情况。

几个经典的模型：

（1）公交车严格按照10分钟一趟发车

这是理论情况，在这种情况下平均等待时间是5分钟

（2）每趟车的时间都是完全随机的

感性上，平均等待时间一定大于5分钟，因为间隔越长之后来的车，覆盖的人越多，所以加权平均下一定高于5分钟。

我们用c++模拟一下循环场景，假设1天有10000个时间单位，有10个车，每个车选择一个随机时间，并且每天都是这个时间。假设这10000个时间单位依次产生1个新的等待者，那么所有人的平均等待时间就是：

int getMinTime()
{
    vector<int>v;
    for (int i = 0; i < 10; i++) {
        v.push_back(rand() % 10000);
    }
    sort(v.begin(), v.end());
    int s = 0, a = 0;
    for (int i = 0; i < 10; i++) {
        int x = (v[(i + 1) % 10] + 10000 - v[i]) % 10000;
        s += x * x;
    }
    return s / 10000 / 2;
}

模拟10000次取平均值：

int main()
{
    int s = 0;
    for (int i = 0; i < 10000; i++) {
        s += getMinTime();
    }
    cout << s / 10000;
    return 0;
}

结果是923

这个结果已经很接近1000了。

实际上，这种循环场景可以用公式推导出来，人均等待时间不是公交车间隔的一半，而是刚好等于公交车平均间隔时间。

（3）瘦弱又文明的你

瘦弱又文明的你，可能挤不上第一辆车，那么你的平均等待时间比公交车平均间隔时间还长！

5，检查悖论

公交车悖论：当你等平均10分钟一班的公交时，理论上你所需等待的平均时间是5分钟，但你总感觉等的时间总比5分钟要长。

如果在公交车悖论中外面不关心具体的平均值，只关心为什么平均值大于5分钟，那原理就是检查悖论。

（1）班级人数抽样

如果在学校抽100个人，统计每个人的班上有多少人，最后总数为s，那么这个学校平均每个班上有s/100人吗？

实际上是小于s/100的，因为班上人更多的班级，有更多的人被抽样了。

（2）友谊悖论

朋友的平均朋友数是高于自己的。

前任的平均前任数是高于自己的。

（3）广义友谊悖论

朋友的平均资产是高于自己的。假如全国人的平均资产是x元，则所有人的所有朋友的资产总和之和除以所有人的所有朋友总数之和，是大于x的。

朋友的平均颜值是高于自己的（这就是为什么每个女生都有漂亮闺蜜？）

（4）堵车抽样

随机问100个司机堵不堵，有80个说堵，但其实只有一小半的道路是堵的，只是这一小半的道路让大部分司机都堵在了对应的路上。

六，决策悖论

1，双信封悖论

（1）双信封悖论PLUS版

在又一个比较诡异的悖论 | Matrix67: The Aha Moments一文中有这么一个问题：

箱子里有两个信封：“一个信封里有1元钱，另一个有10元”有1/2的概率；“一个信封里有10元钱，另一个有100元”有1/4的概率；“一个信封里有100元钱，另一个有1000元”有1/8的概率……也就是说，有1/2^n的概率发生这样的事情，一个信封里有10^(n-1)元钱，另一个信封里有10^n元钱。现在你拿到一个信封，看到了里面有x元钱。给你一次机会换成另外那个信封，问你换不换。

很明显，另外一个信封的收益远高于x，如果按照条件概率来算，另外一个信封的期望是3.4x，那么为什么我们不一开始就选择另外那个信封呢？

（2）双信封悖论

在评论中，我找到了这个问题的简化版，即双信封悖论：

给你两个装钱的信封，其中一只信封中的钱是另一只的两倍，选择一个信封，打开，此时，你可以选择拿走手上信封里的钱，或者拿走另一个信封，问你换不换。

很明显，2个问题的本质是一样的，而且双信封悖论不需要考虑条件概率，一个是x，另外一个就有50%的概率是2x，有50%的概率是x/2，结论仍然是换一个信封期望更高。

（3）双信封悖论简化版

我又看到一些评论，提到，在打开第一个信封之前，期望是无穷大。

于是我想出一个更简单的版本：

给你两个装钱的信封，两个里面的钱都是大于0的随机数（所有大于0的数被选中的概率都是相等的），选择一个信封，打开，此时，你可以选择拿走手上信封里的钱，或者拿走另一个信封，问你换不换。

无论选哪一个，另外一个的期望都是无穷大，所以肯定要换。这个版本其实和前2个的本质也是一样的，但是似乎并不反常识了。

（4）双信封悖论泛化版

上面的例子似乎更让人确信，总期望是无穷大是个关键。

那么我们把Matrix67的问题做个简单的泛化：

箱子里有两个信封：“一个信封里有1元钱，另一个有k(k是大于1的实数)元”有1/2的概率；“一个信封里有k元钱，另一个有k^2元”有1/4的概率；“一个信封里有k^2元钱，另一个有k^3元”有1/8的概率……也就是说，有1/2^n的概率发生这样的事情，一个信封里有k^(n-1)元钱，另一个信封里有k^n元钱。现在你拿到一个信封，看到了里面有x元钱。给你一次机会换成另外那个信封，问你换不换。

此时，另外一个信封的期望是x/3 * (k+2/k)，所以换的条件是k+2/k >=3，即k>=2

而在打开第一封之前，总期望是(1+k)/2 + (k+k^2)/4 + ......，它等于无穷大的条件也是k>=2

2，钱包悖论

A和B两人进行一场赌博。赌法是：由第三者计算A、B二君钱包里面的钱，钱少者可以赢走钱多者的钱。
A对于这场赌博的想法为：若B君的钱比我少，我可能输掉我现有的钱。但若B君的钱比我多，我赢了，就会得到多于我现有的钱。我能够赢的钱比输的钱多，所以这场赌博对我有利。
而B的想法也是如此。但实际上这是一个零和博弈，从而形成悖论。

钱包悖论和双信封悖论类似。如果2个钱包里面的金额都是大于0的随机数，所有大于0的数被选中的概率都是相等的，那么就和上面的“双信封悖论简化版”非常像了。

3，纽卡悖论

一天，一个由外层空间来的超级生物欧米加在地球着陆。欧米加搞出一个设备来研究人的大脑。他可以十分准确地预言每一个人在二者择一时会选择哪一个。
欧米加用两个大箱子检验了很多人。箱子A是透明的，总是装着1千美元。箱子B不透明，它要么装着1百万美元，要么空着。
欧米加告诉每一个受试者：你有两种选择，一种是你拿走两个箱子，可以获得其中的东西。可是，当我预计你这样做时，我就让箱子B空着。你就只能得到1千美元。另一种选择是只拿一个箱子B，如果我预计你这样做时，我就放进箱子B中1百万美元。你能得到1百万美元。
一个男人决定只拿箱子B。他的理由是——我已看见欧米加尝试了几百次，每次他都预计对了。凡是拿两个箱子的人，只能得到1千美元。凡是只拿箱子B的，都变成一个百万富翁。
一个女孩决定要拿两个箱子，她的理由是——欧米加已经做完了他的预言，并已离开。箱子不会再变了。如果是空的，它还是空的。如果它是有钱的，它还是有钱。所以我要拿两个箱子，就可以得到里面所有的钱。
你认为谁的决定最好？

4，老虎悖论

国王要处决一个囚犯，但给他一个生还的机会。囚犯被带到5扇紧闭的门前，他知道其中一扇后面关着一只老虎。国王对囚犯说：“你必须依次打开这些门。我可以肯定的是，在你没有打开关着老虎的那扇门之前，你无法知道老虎是在那扇门后。”

开门之前，囚犯进行了如下分析：
　　假如老虎在第五扇门，那当他把前四扇门打开后都没发现老虎，那他肯定猜到老虎在第五扇门中，因国王说过不论何时他也料不到老虎在哪扇门后，那国王的说话就错了。因此，老虎肯定不在第五扇门中。
　　同样道理，老虎也不在第四道门中，否则囚犯打开三道门后，只剩两道门，老虎既不在第五扇门后，那就会给他料到在第四扇门后；
　　依次类推，老虎不存在任何一道门后，从而形成悖论。

我的理解：

首先，5个门后面有且仅有一个后面有老虎，这个是毫无疑问的，我觉得这个不属于质疑的对象。

其次，国王的结论是错的，因为如果前四扇门都没有老虎，那么囚犯就知道了老虎在最后一扇门后面。

所以，既然国王的结论是错的，那么当前三扇门都没有老虎的时候，囚犯并不能推导出老虎在第四扇还是第五扇门后面。

结论就是，国王的结论是错的，所以囚犯没有得到足够的信息，如果老虎在第五扇门，囚犯就会提前知道，否则，囚犯就无法提前知道。

5，群体决策悖论

假设全市所有人一起玩一个游戏，每个人选中0-100的一个数字，所有人同时做出选择，然后统计所有数的平均数。最后谁选中的数字最接近平均数的2/3，则获得超级大奖，那么应该怎么选择？

思路一：

首先假设所有人都是随机选，那么平均数是50。

再假设每个人都足够理性，那么应该选择50*2/3=33，平均数变成33

既然平均数是33，那么应该选择33*2/3=22

以此类推，22*2/3=1,5,15*2/3=10,10*2/3=7,7*2/3=5,5*2/3=3，3*2/3=2,2*2/3=1，

最后，1*2/3=1，至此终于稳定下来，所以最佳选择是1（并不是一些人认为的0）

PS：这里有2条假设，先假设所有人都是随机选，后又假设每个人都足够理性，显然整个逻辑是不自洽的。

思路二：

假设每个人都足够理性，首先平均数不超过100，所以每个人选择的数字应该都不超过67。

注意，每个人都足够理性，每个人都使用相同的策略，不代表每个人选择的数字都一样，因为可能是混合策略，而不是纯策略。

继续推理，平均数不超过67，那么每个人选择的数字应该都不超过67*2/3=45,

以此类推，45*2/3=30,30*2/3=20，20*2/3=13,13*2/3=9,9*2/3=6,6*2/3=4,4*2/3=3，3*2/3=2,2*2/3=1

所以，每个人选择的数字应该都不超过1

最后我们只能说最佳选择是0或者1，具体该选择0还是该选择1，或者是某种混合策略，已知条件是不足以推导出来的。

实际情况：

据网友实测，找了2000人测试，平均数是43，所以选择29的赢了。当然，奖品肯定不是万众瞩目的超级大奖这种level的，所以这2000人里面肯定有一些闭着眼睛乱选的。

为什么实际情况会和理论推导差别这么大呢？因为现实世界中，足够理性的人是极少数的。

6，三门悖论

在美国的一个电视节目中，参与者面前有三扇门，其中一扇门后面有奖品，另外两扇门后面的空的。

首先参与者选择其中一扇门，然后主持人会在剩下的2扇门（有1扇或者2扇是空门）中选择一扇门打开，表示这是空门。

此时还剩下2扇门，参与者有一次重新选择的机会，这个问题的关键在于，剩下的2扇门有奖品的概率，是1/3+2/3还是1/2+1/2呢？

这个问题曾经引起全社会广泛的讨论，2种说法都有一定的道理，但实际上肯定有一种是错的。

（1）正确答案

一开始有1/3的概率选中有奖品的门，这种情况下应该不换门。

一开始有2/3的概率选中没有奖品的门之一，这种情况下应该换门。

综合来看，剩下的2扇门有奖品的概率分别是1/3和2/3

（2）基于信息的概率模型

很多人对1/3+2/3很确信，对1/2+1/2嗤之以鼻，当然也有人坚定的认为就是1/2+1/2。
能理解到这两种思路貌似都有一定的合理性的人，确实只占极少数。
引申一步，其实大部分人是没有真正懂“悖论”这个概念的，他们只觉得***悖论很荒谬。
悖论就好像是一个解题过程，由已知条件A首先推导出B，然后B推导出C，然后C推导出D，然后D推导出E。
但是我们知道E一定是错的，关键是这4步推理看起来都有道理。
往往我们需要很严格，很细致的论证，才能发现原来第3步是错的。
但是很多人一看到这个悖论，就嗤之以鼻，说A推导出B不对，其实他压根就没有理解ABCDE这个推导过程。
言归正传，三门问题我个人理解不是条件概率，而是概率模型，当然二者很像。
什么是概率模型呢，举个例子，你和张三要猜拳，一局定胜负，赢的人获得1元，你觉得对方出石头，剪刀，布的概率都是1/3。
那么1/3这个值是怎么来的？这是一个默认通用模型：“在n个球中选一个，每一个被选中的概率都是1/n”。
但是如果游戏规则是，你和张三要猜拳，一局定胜负，赢的人获得10000元，
那么你可能会仗着对方不会上网，选择上网搜索，然后你发现现实生活中，概率不是1/3+1/3+1/3，而是0.36+0.31+0.33。
这就是2种不同的概率模型，本质上是有信息和没有信息的区别，有信息就会有对应的概率模型。没信息就只能用默认通用模型
所以说，在三门悖论中推导出1/2+1/2的，该思路的错误之处在于，对于剩下的2扇门，认为都有可能中奖，而且一开始是对称的地位，现在也应该是对称的地位，所以都是1/2。但是，此时我们其实是有信息的，有信息就不能用默认通用模型了。
一个是一开始三选一选的门，一个是剩下的两个门去掉一个留下的门，显然是有信息的，那么把这一个信息转化成概率模型，就是1/3+2/3了。

（3）后验概率

我上面总结的基于信息的概率模型，应该是和概率论中的后验概率是一样的。

七，关于归纳的悖论

1，乌鸦悖论

我们可以出去观察成千上万只乌鸦，然后发现他们都是黑的。在每一次观察之后，我们对“所有乌鸦都是黑的”的信任度会逐渐提高。归纳法原理在这里看起来合理的。

现在问题出现了。“所有乌鸦都是黑的” 的论断在逻辑上和“所有不是黑的东西不是乌鸦”等价。如果我们观察到一只红苹果，它不是黑的，也不是乌鸦，那么这次观察会不会提高我们对“所有乌鸦都是黑的”的信任度？

有些哲学家认为其实这个命题是完全正确的，出错的是我们自己的逻辑。其实观察到一个红色的苹果确实会增加乌鸦都是黑色的可能性！这就相当于：如果有人把宇宙中所有不是黑的物体都给你看，而你发现所有的物体都不是乌鸦，那你就完全可以断定所有乌鸦都是黑色的了。这个“悖论”看上去荒谬只是因为宇宙中 “不是黑色的”物体远远多于“乌鸦”，所以发现一个“不是黑色的”物体只增加了极其微小的对于“乌鸦都是黑色的”的信任度，而相对而言，每发现一只黑色的乌鸦就是一个有力的证据了。

我的思路：和上面这个哲学家的思路类似，不是所有物体都是可数的可分割的，而且一个物体也可能不是纯色的，很难论断是不是黑色的。

八，关于心理学的悖论

1，阿莱悖论

在80%获得4000和100%获得3000之间做选择，一般人会选择100%获得3000，在80%损失4000和100%损失3000之间做选择，一般人会选择80%损失400。

九，其他悖论

1，费米悖论

银河系大约有2500亿颗恒星，可观测宇宙内则有700垓（7 x 10^22）颗。即使智慧生命以很小的概率出现在围绕这些恒星的行星中，那么仅仅在银河系内就应该有相当大数量的文明存在。这也符合平庸原理的观点，即地球不是特殊的，仅仅是一个典型的行星，具有和其他星体相同的规律和现象。

考虑到智慧生命克服资源稀少性的能力和对外扩张的倾向性，任何高等文明都很可能会寻找新的资源和开拓他们所在的恒星系统，然后是涉足邻近的星系。因为在宇宙诞生137亿年之后，我们没有在地球或可观测宇宙的其他地方，找到其他智慧生命存在的切实可靠的证据；可以认为智慧生命是很稀少的，或者说我们对智慧生命的一般行为的理解是有误的。

费米悖论的核心就是，外星高等文明到底存不存在。