1、矩阵和行列式
矩阵的知识是从行列式而来,矩阵和行列式的区别在于矩阵是一张表,行列式是一个数。
如下,
A是一个矩阵:
(1) A = [ 1 2 3 4 5 6 7 8 9 ] A = \left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right] \tag{1} A=⎣⎡147258369⎦⎤(1)
B是一个行列式:
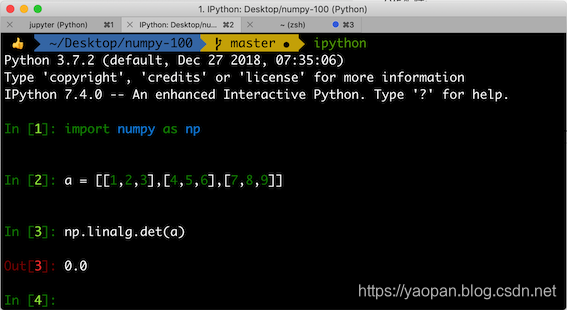
(2) B = ∣ 1 2 3 4 5 6 7 8 9 ∣ = 0 B = \left| \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right| \tag{2}=0 B=∣∣∣∣∣∣147258369∣∣∣∣∣∣=0(2)
2、矩阵和向量
向量是一个特殊的矩阵,其行或列数目为1。
矩阵A的一个3*1的列向量
x
⃗
\vec x
x为:
(3) x ⃗ = [ 1 4 7 ] \vec x = \left[ \begin{matrix} 1 \\ 4 \\ 7 \end{matrix} \right] \tag{3} x=⎣⎡147⎦⎤(3)
A的一个1*3的行向量 y ⃗ \vec y y为:
(4) x ⃗ = ∣ 1 2 3 ∣ \vec x = \left| \begin{matrix} 1 & 2 & 3 \\ \end{matrix} \right|\tag{4} x=∣∣123∣∣(4)
3.向量范数
向量范数: 给向量赋予一个正标量值,或者简单理解为向量的模。
(5)
z
⃗
=
[
1
4
7
]
\vec z = \left[ \begin{matrix} 1 \\ 4 \\ 7 \end{matrix} \right] \tag{5}
z=⎣⎡147⎦⎤(5)
向量 z ⃗ \vec z z的模记通常记作 ∣ ∣ z ⃗ ∣ ∣ ||\vec z|| ∣∣z∣∣(或 ∣ ∣ z ⃗ ∣ ∣ 2 ||\vec z||_2 ∣∣z∣∣2) :
(5) ∣ ∣ z ⃗ ∣ ∣ = [ 1 4 7 ] = 1 2 + 4 2 + 7 2 ||\vec z||= \left[ \begin{matrix} 1 \\ 4 \\ 7 \end{matrix} \right] \tag{5} = \sqrt{1^2+4^2+7^2} ∣∣z∣∣=⎣⎡147⎦⎤=12+42+72(5)
范数有不同的计算方法,上面介绍的是比较常用的求模方法,向量还有其他范数:
向量的1范数(L1范数): 各元素的绝对值之和::
∣ ∣ X ⃗ ∣ ∣ 1 = ∑ i = 1 n X i ||\vec X||_1=\sum_{i=1}^nX_i ∣∣X∣∣1=i=1∑nXi
向量的2范数,各元素平方和再开根号:
∣ ∣ X ⃗ ∣ ∣ 2 = ∑ i = 1 n X i 2 ||\vec X||_2=\sqrt{\sum_{i=1}^nX_i^2} ∣∣X∣∣2=i=1∑nXi2
向量的p范数,各元素绝对值的p次方再开q次方:
∣ ∣ X ⃗ ∣ ∣ P = ( ∑ i = 1 n ∣ X i ∣ p ) 1 / p ||\vec X||_P =( \sum_{i=1}^n|X_i|^p)^{1/p} ∣∣X∣∣P=(i=1∑n∣Xi∣p)1/p
向量的无穷范数,元素绝对值最大者:
∣
∣
X
⃗
∣
∣
∞
=
∑
i
=
1
n
max
(
∣
X
⃗
∣
i
)
||\vec X||_\infty = \sum_{i=1}^n\max(|\vec X|_i)
∣∣X∣∣∞=i=1∑nmax(∣X∣i)

4. 矩阵范数
矩阵的1-范数:
矩阵的每一列上的元素绝对值先求和,再从中取个最大的. (列和最大)
矩阵的2-范数(谱模):
二范数指矩阵A的2范数,就是A的转置共轭矩阵与矩阵A的积的最大特征根的平方根值,是指空间上两个向量矩阵的直线距离。类似于求棋盘上两点间的直线距离。
矩阵的无穷范数(行模)
矩阵的每一行上的元素绝对值先求和,再从中取个最大的M,(行和最大)
参考文章
https://blog.csdn.net/zaishuiyifangxym/article/details/81673491
https://blog.csdn.net/bendanban/article/details/44221279
https://www.cnblogs.com/freyr/p/4533048.html
https://wenku.baidu.com/view/a27808cd941ea76e58fa04b3.html





 博客介绍了矩阵和行列式的区别,矩阵是表,行列式是数。还指出向量是特殊矩阵。详细讲解了向量范数,如常用求模方法及1范数、2范数等不同计算方式,也介绍了矩阵的1 - 范数、2 - 范数和无穷范数的计算方法。
博客介绍了矩阵和行列式的区别,矩阵是表,行列式是数。还指出向量是特殊矩阵。详细讲解了向量范数,如常用求模方法及1范数、2范数等不同计算方式,也介绍了矩阵的1 - 范数、2 - 范数和无穷范数的计算方法。

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










