基于2D多边形的碰撞检测和响应(七)

七、动态刚体

为了不浪费时间介绍动态刚体，可以直接参参见下面的连接：

http://www.d6.com/users/checker/dynamics.htm#articles

这里，展示了如何在2D游戏中实施真实的物理。

我将介绍一些我所做的扩展，首先，计算给定凸多边形的惯量是有技巧的。需要提醒你的是，惯量适用于角度变化，质量适用于线形变化。较高的惯量对应于较大的质量，在这种情况下物体将很难旋转。相反，较小的惯量使得物体的角速度更易改变。

 

质量和惯量是有联系的，因为它们都依赖于体积，密度和物体的平衡，下面的连接给出了一些参考

http://www.physicsforums.com/showthread.php?s=e251fddad79b926d003e2d4154799c14&t=25293&page=2&pp=15

一句话，计算惯量的公式为：

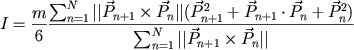
这里：

M是质量，N是顶点数，Pn是多边形的一个顶点，||..||表示求模运算。在2D中表示向量的长度。

可以使用下面的公式根据组成多边形材质的密度来计算惯量

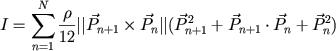
这里：P是密度，N是顶点数, Pn是多边形的顶点, ||..||表示求模，从上述方程中，你可以推理出计算质量的等式。

该系统的其它模式是处理交叠。这可以避免一个物体陷入另一个物体，因为使用推力计算在低速的时候是非常不精确的。为了解决交叠问题，即简单的方法是沿着碰撞法线根据碰撞深度将物体推开。当然只有在检测到交叠的时候才使用它。

 

为了使它更为精确，物体的移动应该依赖于它们质量的比率，因此较轻的物体应该移动更多，而较重的物体移动较少，当然具有无穷大质量的物体是不会移动的。

 

至于摩擦力，基本的是动态摩擦力，它将沿着物体速度的反向添加一个力，大小为||u*Jn||其中u是动摩擦系数Jn是压力。

 

静态摩擦力总是比较简单的模型。我选则的静态摩擦力的模型是将物体与一个不可见的物体在碰撞平面上发生碰撞。正碰撞的计算是非常简单的。碰撞力的方向是速度的反向，触点的速度会被抵消（基本上，恢复系数稍微比1大）

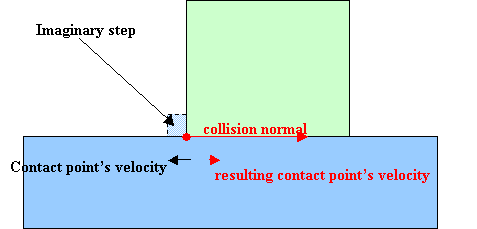
好了，剩下的部分就按照Chris Hecke的教程。物体翻转，碰撞，做一系列疯狂的事情，并且看起来非常的真实。