大话EM算法

        在进入EM算法之前，我们先来看一个高斯混合模型的问题。混合高斯模型能很好的拟合数据的分布，这是正太分布非常好的一个性质。现在有m个样本数据，认为这m个数据样本是符合正太分布的，也就是说这些数据是正太随机变量的采样点，要求出这样的正太分布，使这些采样点分布到这个正太分布的可能性最大。这里的正太分布不是单个的正太分布，而是多个正太分布组成的混合高斯模型。对于这类求概率模型参数的问题一般解法是采用对数似然估计，可以很快的求得模型参数。然而对于混合高斯模型这类特殊的问题，对数似然估计法显得的无能为力，因为对数中的混合高斯模型是多项式加和的形式，很难像一般对数似然估计方法那样直接求导。那么如何解决这个问题呢，这正是EM算法所要解决的，

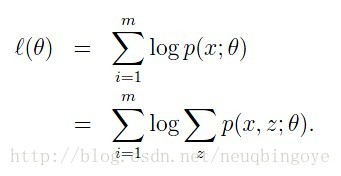
        EM算法是一种解决存在隐含变量优化问题的有效方法，既然不能直接最大化log（），我们可以不断建立l的下届（E步），然后优化下届（M步），不断迭代得到最优值。下面回到求解混合高斯模型的问题，在模型中引入隐含变量Z，通常如果能够求得Z，最大似然估计的问题就很容易解决。