Normal Equation是一种基础的最小二乘方法,本文将从线性代数的角度来分析Normal Equation(而不是从矩阵求导 matrix derivative 的角度)。
很多作者(特别是智商比较高的)在推导公式的时候有意无意的忽略了思考过程,只留下漂亮的步骤。这让很多读者(比如说我)跟不上节奏,最后一头雾水。本文将从求解“貌似无解”的方程组入手,再讲讲投影(Projection)的使用,最后进入到Normal Equation的应用。我的目的是让和我一样蠢的孩子对这个重要公式有一个Big Picture——即使忘记了也可以重头推出。
更新记录:
更新1 增加了对 的使用解释(偏导数证明)
的使用解释(偏导数证明)
一、求解不可解的方程组
先看一个最最简单的例子——
例1.0 如图,在
空间中有两个向量,求一个常数
使两个向量满足
。
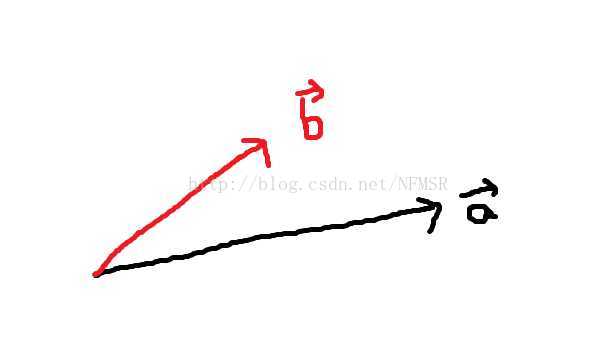
这个方程明显不可解,因为 与
与 不共线,无法通过对
不共线,无法通过对 数乘得到
数乘得到 。
。
再看下一个比较简单的例子——
例2.0 在
空间中的平面
有一组基
和
,如图所示,求出常数
与
使向量
满足条件
。
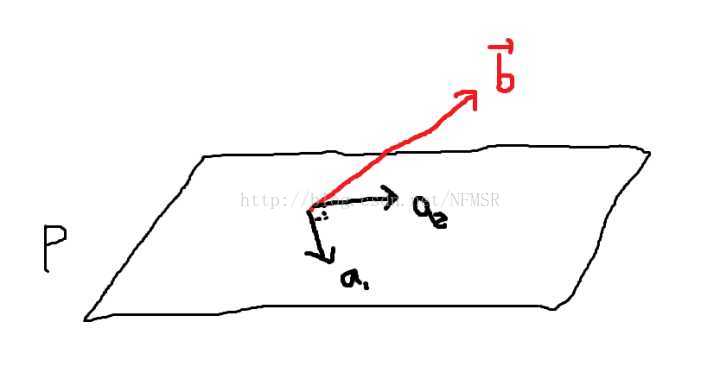
这个方程也明显不可解,因为 不在平面
不在平面 上,而
上,而 与
与 的线性组合只能得到平面上的向量。
的线性组合只能得到平面上的向量。
以上两个问题非常的典型,因为在解决实际问题的时候,我们很难得到Perfect Solution,我们只能尽力而为的争取Best Solution。以上两个例子明显没有做到perfect(连基本的方向都错了),那么如何找到best solution呢?
二、投影的应用
思路很简单:我们只要找到一个 使
使 方向上的向量
方向上的向量 距离
距离 最近。
最近。
回到最简单的例子
如图,在空间中有两个向量,求一个常数
使两个向量满足
。
现在应该如何寻找 的解呢?
的解呢?
最好的方法就是抛弃 向量中垂直
向量中垂直 的分量,只要计算
的分量,只要计算 使
使 等于向量
等于向量 在
在
方向的分量(即 在
在 上的投影(Proj)
上的投影(Proj) ),同时我们把向量
),同时我们把向量 垂直
垂直 方向的分量称为
方向的分量称为 (error)。
(error)。
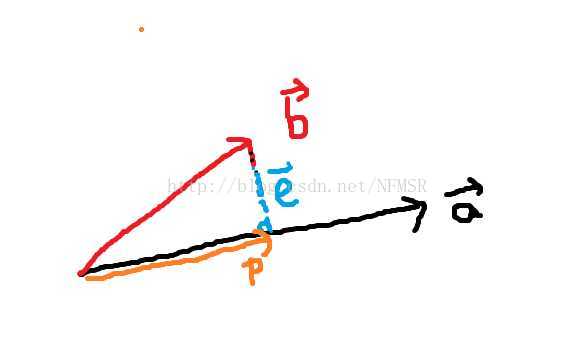
原来的问题 变成了求解
变成了求解 (
( 是
是 的估计量)
的估计量)
因为 与
与 合成了
合成了 向量(
向量( ),而且
),而且 垂直于
垂直于 (
(),所以我们得出了一个非常重要的结论(敲黑板)!!!核心啊!!!

(这里转置的符号应该去掉,然后下面的的叉乘符号改成点乘,向量叉乘结果还是一个向量。之所以可以有转置是因为在利用向量内积后theta等号右边的公式中a*b(点乘)可以改写成aT*b,而转置后确实可以更好地应用到高维也就是矩阵中。)
这个方程的核心就是写成向量内积形式的 与
与 的垂直关系,只不过
的垂直关系,只不过 被拆开书写。其实这个方程也可以写作
被拆开书写。其实这个方程也可以写作 ,但是写作转置向量
,但是写作转置向量 的形式可以让这个方程更自然的拓展到高维。好了,我们继续改写方程……
的形式可以让这个方程更自然的拓展到高维。好了,我们继续改写方程……


在这一步我们就得到了best的 ,但考虑到这并不perfect,所以我们称之为
,但考虑到这并不perfect,所以我们称之为 。
。
P.S.如果想用投影矩阵P来简化从 转换到
转换到 的过程,可以把
的过程,可以把 的结果带入到
的结果带入到 中。我们发现投影矩阵
中。我们发现投影矩阵 在形式上就等于乘数
在形式上就等于乘数 ,即
,即 满足
满足 。
。
现在我们再看看怎么在 中解决不可解方程。
中解决不可解方程。
例2.0 在空间中的平面
有一组基
和
,如图所示,求出常数
与
使向量
满足条件
。
平面 有基向量
有基向量 和
和 ,故
,故 可以表示成基的线性组合
可以表示成基的线性组合 ,即
,即
令基向量组成的矩阵 ,参数组成的向量
,参数组成的向量 ,与平面垂直的误差向量
,与平面垂直的误差向量 。(这里插一句话,最小二乘法的核心就是找出一个
。(这里插一句话,最小二乘法的核心就是找出一个 就是让
就是让最小化)
我们发现在 中的问题
中的问题 在这里拓展成为了
在这里拓展成为了 。
。
相应的, 问题在这里拓展成了
问题在这里拓展成了 ,其中
,其中 。
。
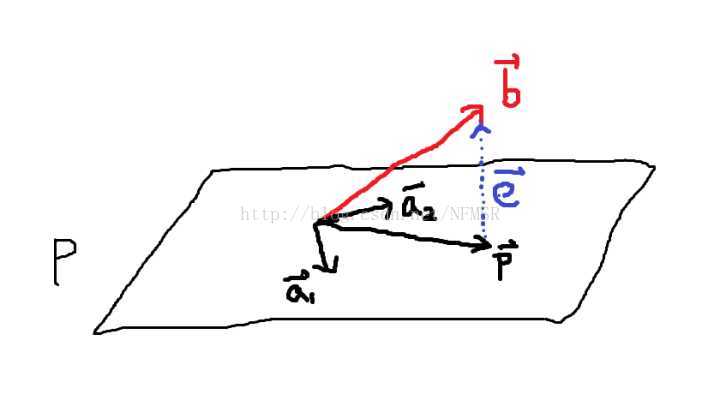
还是一样的套路,我们还是从垂直关系入手——因为 ,而且
,而且 ,所以有以下方程组——
,所以有以下方程组——

整理成矩阵的形式——

(敲黑板!!!敲黑板!!!)

写到这里回头看看 情景下的核心公式
情景下的核心公式 ,可以这家伙换一套马甲又出现了!!!看来方程
,可以这家伙换一套马甲又出现了!!!看来方程 是一种高维的拓展。我们可以把
是一种高维的拓展。我们可以把 中的
中的 看成一个只有一列的矩阵。
看成一个只有一列的矩阵。
我们继续整理这个公式——


写到这里我们就没什么可以干的了。
有人可能想说——明明还可以继续化简啊!!!
但实际的情况中,我们不能保证矩阵 总是方阵(square),但是
总是方阵(square),但是 总是可以保证是方阵。因为只有方阵才有逆矩阵,所以我们只能保证有
总是可以保证是方阵。因为只有方阵才有逆矩阵,所以我们只能保证有 ,而不能保证有
,而不能保证有 。
。
所以我们只能回到 这里。如果你有读过Andrew Ng著名的公开课CS229的Lecture Notes,你一定记得他用矩阵求导得出的Normal Equation——
这里。如果你有读过Andrew Ng著名的公开课CS229的Lecture Notes,你一定记得他用矩阵求导得出的Normal Equation——

你会发现除了 和
和 不一样以外,我们已经把Normal Equation(
不一样以外,我们已经把Normal Equation( )推出来了……我居然在下一部分还没有开始讲就把内容说完了,场面一度非常尴尬啊。可见从投影推出Normal Equation是一件多么自然的事情啊~~~我都不知道哪里切开。
)推出来了……我居然在下一部分还没有开始讲就把内容说完了,场面一度非常尴尬啊。可见从投影推出Normal Equation是一件多么自然的事情啊~~~我都不知道哪里切开。
说到这里先总结一下投影的几个意义(敲黑板)!!!
 的所有可能结果都在一个固定的区域中,在线性代数中我们称这个区域为列空间(column space),列空间顾名思义就是矩阵各列的所有线性组合
的所有可能结果都在一个固定的区域中,在线性代数中我们称这个区域为列空间(column space),列空间顾名思义就是矩阵各列的所有线性组合 。在1-D的情况下列空间就是一条线,在2-D的情况下列空间就是一个平面。但是我们的数据哪里会这么恰好的落在矩阵的列空间里呢?天底下哪有这样的好事啊!!!
。在1-D的情况下列空间就是一条线,在2-D的情况下列空间就是一个平面。但是我们的数据哪里会这么恰好的落在矩阵的列空间里呢?天底下哪有这样的好事啊!!!
 会成为一个
会成为一个
 矩阵(如下图)。在这种等式数量远大于未知数数量的情况中,我们很难满足每一个等式的约束。
矩阵(如下图)。在这种等式数量远大于未知数数量的情况中,我们很难满足每一个等式的约束。

但是目标不再在空间里并不代表不能求出解,只能说没有perfect solution(语出Gilbert Strang),但是我们努力一下还是可以做到最好的(best solution)。我们用投影向量 来寻找最合适的
来寻找最合适的 。
。 就是并不存在的完美解
就是并不存在的完美解 的估计值。
的估计值。
三、Normal Equation应用
既然Normal Equation在上文都推导完了,这里我们就随便带几个数据来玩玩咯。练手案例 找一条直线来拟合点 (1,1)、(2,2)、(3,2)
我们如果用一条直线来拟合的话,设
,我们先得到以下值——





我们发现
很遗憾的没有解,于是我们左右各乘上
,祭出了投影大招——
。
再把这个方程变换成Normal Equation:
带入数值在Matlab中小跑一下就得到了结果
即直线
是上述三个点的拟合结果。
四、其他想说的话
1.关于 的暴力使用
的暴力使用
在前一步可以不用判断是否可解,可以直接使用 。事实上,在最小二乘时遇到长方形矩阵
。事实上,在最小二乘时遇到长方形矩阵 ,我们就可以用上
,我们就可以用上 替代
替代 计算。这是是一种路子很野的但是很简单实用的经验规则,可以简单实验如下——
计算。这是是一种路子很野的但是很简单实用的经验规则,可以简单实验如下——
用直线拟合三个点 (1,1)、(2,2)、(3,2)时,自然希望 真实值和估计值的误差
越小越好。

分别对
和
求偏导数等于的零的值——


整理以上公式我们得到了方程组——

再整理一下,把这个方程写成矩阵乘法的形式——

在最后一步整理以后我们发现刚才千辛万苦算出来的
就是上文的
啊!!!
说明这个经验方法是可以信得过的!!!
2.关于化简的问题
因为投影的性质非常美妙,如果矩阵 是各行线性无关的方阵(square),说明存在
是各行线性无关的方阵(square),说明存在 ,则Normal Equation会变成如下形式——
,则Normal Equation会变成如下形式——
说明如果存在一个perfect solution,该解不会受到影响。
3.多次投影有影响吗?
已经在空间中的向量乘上投影矩阵 仍然等于本身,二次投影不会有任何副作用!也就是说
仍然等于本身,二次投影不会有任何副作用!也就是说 。证明如下——
。证明如下——
五、参考资料
1.Gilbert Strang Introduction to Linear Algebra 4.2 Projection 4.3 Least Squares Approximations
2.Andrew Ng CS229 Lecture Note 1 Supervised learning/The normal equations
六、最后的话
列空间没展开讲不知道有没有必要。
笔力不够好,想象中应该写的更简单易懂的,但是没有达到效果,会再更新。
欢迎拍砖!!!
转自:https://zhuanlan.zhihu.com/p/22757336
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








