6. 深度学习实践：深度前馈网络（续）

接上篇：6. 深度学习实践：深度前馈网络

5. 架构设计

5.1 深度

万能近似定理：一个FNN如果具有线性输出层和至少一层具有任何一种挤压性质的激活函数的隐藏层，只要给予网络足够数量的隐藏单元，它能够以任意精度来近似任何从一个有限维空间到另一个有限维空间的Borel可测函数。

该定理意味着：无论我们试图学习什么函数，一个大的MLP一定能够表示这个函数。很完美，是不是？

但是，我们不能保证训练算法能够学得这个函数。一是优化算法可能找不到用于期望函数的参数值。二是训练算法可能过拟合而选择了错误的函数。

no free lunch 告诉我们，不存在万能的过程，既能够验证训练集上的特殊样本，又能选择一个函数来扩展到训练集外的点。

具有单层的FNN足以表示任何函数，但是网络层可能大得无法实现，无法正确学习和泛化。怎么办？使用更深的模型，可以减少期望函数所需的单元的数量，同时可以减少泛化误差。

• Montufar et al. (2014)指出：具有$d$个输入，深度为$l$，每个隐藏层$n$个单元的深度整流网络可以描述的线性区域的数量是：

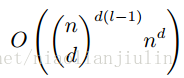
即其是深度的指数级的函数。那么增加深度就很好了。当然不保证所有都有这样的性质，但提供了某种方面的支撑。

• 隐含的先验：深度模型暗合了我们想要学得的函数应该是若干个更简单的函数的组合。
• 表示学习的角度：学习的问题包含着发现一组潜在的变差因素，可以根据其他更简单的潜在变差因素来描述。
• 计算机程序：每个步骤使用前一步骤的输出。中间值传递。

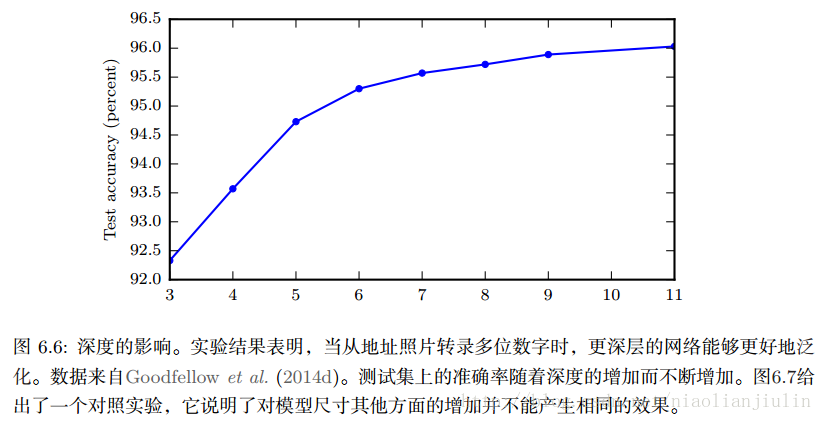
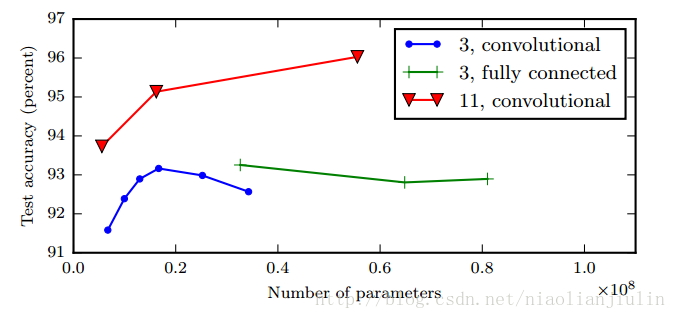
一图胜千言。根据经验，更深的模型似乎确实在广泛任务中泛化得更好，也算提供了先验。

5.2 其他考虑

杂谈。

特定任务上：用于CV的CNN，用于序列处理的RNN。有其自身考虑。

许多架构构建了一个主链，添加了额外的架构，比如从更高层的跳跃链接，使得梯度更容易从输出层流向浅层。（想起FCN了）

如何将层与层间连接起来？FNN用矩阵描述的线性变换。一些专用网络具有较少连接，减少了参数量，但通常高度依赖于问题。如CNN用于CV的稀疏连接。

6. BP算法及其他

关于BP算法，在CS231n课程中已学习，并手推、程序伪代码都已见识过。应该说讲得很清楚。此处浏览下书的内容做补充。

• 误区1：BP算法是用于多层神经网络的整个学习算法？

实际上BP仅仅指用于计算梯度的方法。另一种算法，如SGD算法，则利用该梯度进行学习。

• 误区2：BP仅适用于多层神经网络？

原则上BP可以计算任何函数的导数。在学习算法中，最常需要的梯度是代价函数关于参数的梯度，BP可算但不局限于此。

6.1 链式法则

概率中的链式法则：

P(