Montufar et al. (2014)论文一些有趣的想法

最新推荐文章于 2024-07-08 22:19:32 发布

早日地中海

最新推荐文章于 2024-07-08 22:19:32 发布

阅读量57

点赞数 1

文章标签：神经网络深度学习

本文链接：https://blog.csdn.net/Zhe_Lin/article/details/134852273

版权

Montufar et al.(2014)指出一些用深度整流网络表示的函数可能需要浅层网络(一个隐藏层)指数级的隐藏单元才能表示。

同时指出分段线性网络（可以通过整流非线性或maxout单元获得）可以表示区域的数量是网络深度的指数级的函数。图6.5解释了带有绝对值整流的网络是如何创建函数的镜像图像的，这些函数在某些隐藏单元的顶部计算，作用于隐藏单元的输入。

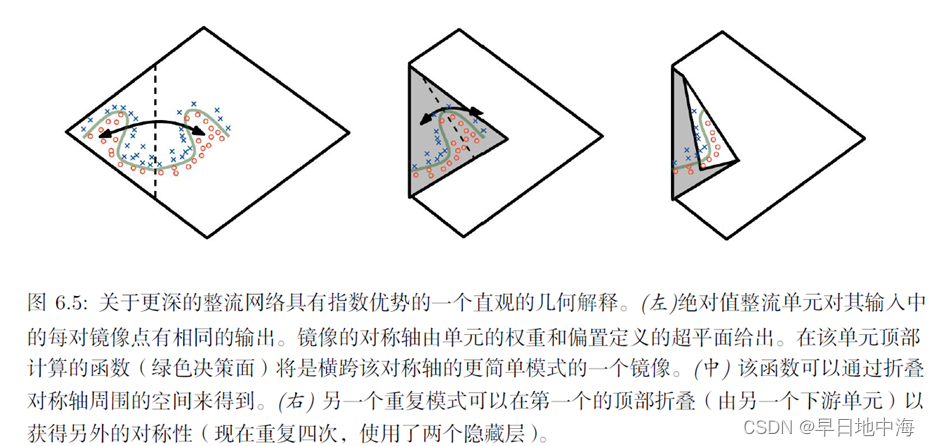
图来源于花书。

读书读到这里的时候，个人感觉花书给出的解释很难读懂，也有可能是自己的能力有限。于是我大致读了一遍这篇文章，产生了一些奇奇怪怪的想法，想从数学上来说明这个图到底在讲些什么？

从一个简单的例子出发：

首先，论文中给出一个定理：

定理1：如果存在一个映射F，这个映射将其输入域中两个不同的子集(或邻域)S和T映射到输出域的一个公共子集，也就是F(S)=F(T). 我们称S和T可以被F所表示。

推论：当然，如果输入域中不止有两个邻域，比如说四个子集(或邻域)A,B,C,D，通过映射F, s.t. F(A)=F(B)=F(C)=F(b), 我们称A,B,C,D可以被F表示。

由上面的这个定理，我们可以对欧几里得空间中四个象限作为一个输入域中的四个子集，那么我们定义一个映射 $g: \mathbb{R}^2\rightarrow \mathbb{R}^2; (x_1, x_2)\mapsto (|x_1|, |x_2|)$ ，我们可以称这四个象限可以被g所表示。（因为四个象限中的元素经过绝对值映射之后，都对应到了第一象限）

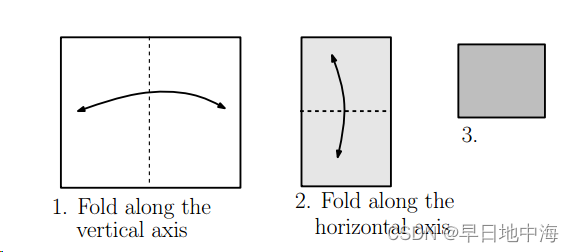
发散思维，上面所说的绝对值映射其实就是将一张纸，折叠两次的结果，得到下图3这一个子集

上面所提及到的只是在欧几里得空间中一个点。有了点，我们当然可以想到，点变成直线，曲线等数学函数，也就是如果在四个象限中分布着一条直线（或曲线），我们该怎么样表示这样的操作？

我们知道，神经网络中其中一层可以分解为一个仿射变换+非线性激活来表示，那么我们大可以将仿射变换得到的输出作为我们“四个象限中的元素”，再将非线性激活函数激活函数定义为我们上面定义的映射g，这样，空间中两次翻折现象等价于神经网络中隐藏层的一层的效应。

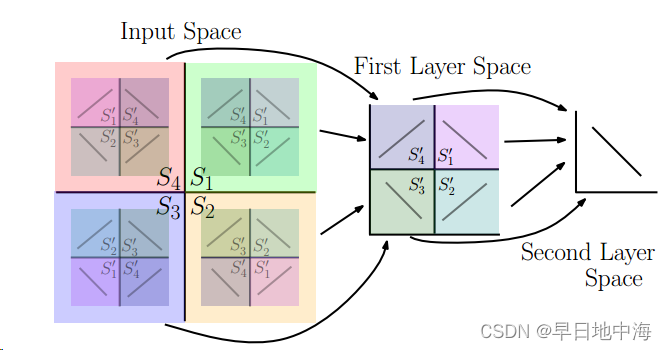
上图可以表示两次“二次翻折”现象，通过两个隐藏层来表示，仿射变换的输出可以作为第一象限中的这条直线。

回到正题：

OK，有了上面的理解，我们就可以进一步解释图6.5的具体含义了。抛出问题：上面都是按照以坐标轴作为对称轴进行翻折，那么如果在欧几里得空间中，我们是否可以随机给出一条直线进行翻折？

比如说在二维坐标系中，我们随机有一个点 $x=(x_1, x_2)$ ，再随机给出一条直线 $l_1: {\bf w}^T{\bf x}+{\bf b}=0$ ，这里w和b都是向量，如图所示：

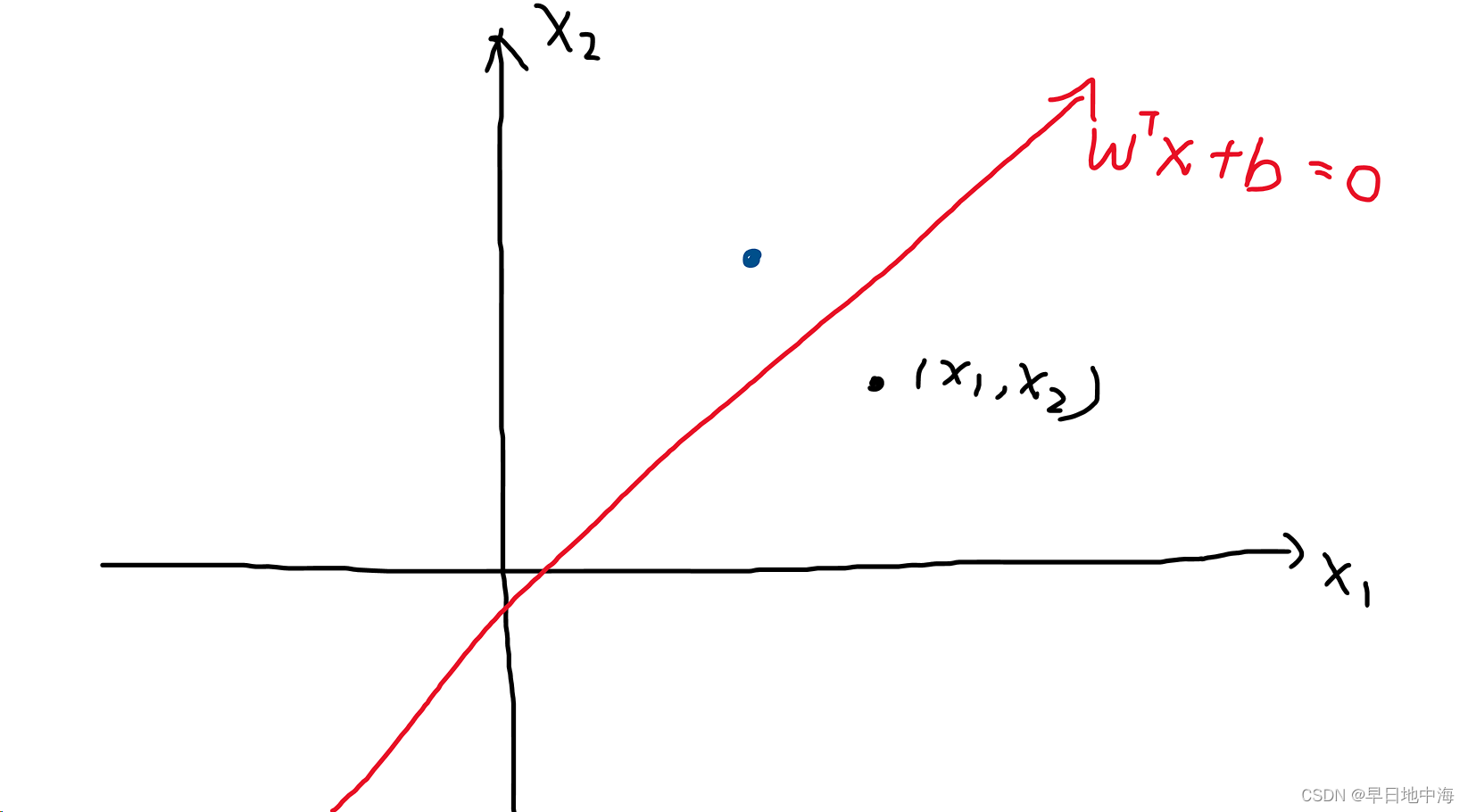
如果我们想按照 $l_1$ 这条直线进行翻折，把x这个点映射到对称轴的另一边（蓝色的点），那该怎么做？我们可以将 $l_1$ 这条线作为新的坐标轴的一个横轴，设为 $x_1'$ ，再建立其纵坐标，也就是 $x_1'$ 的法向量 $x_2'$ （纵轴的位置可以随便取，大可以将纵轴穿过我们的对称点，不影响后续操作）。那么我们的点x在新的坐标系下的坐标可以设为 $(x_1', x_2')$

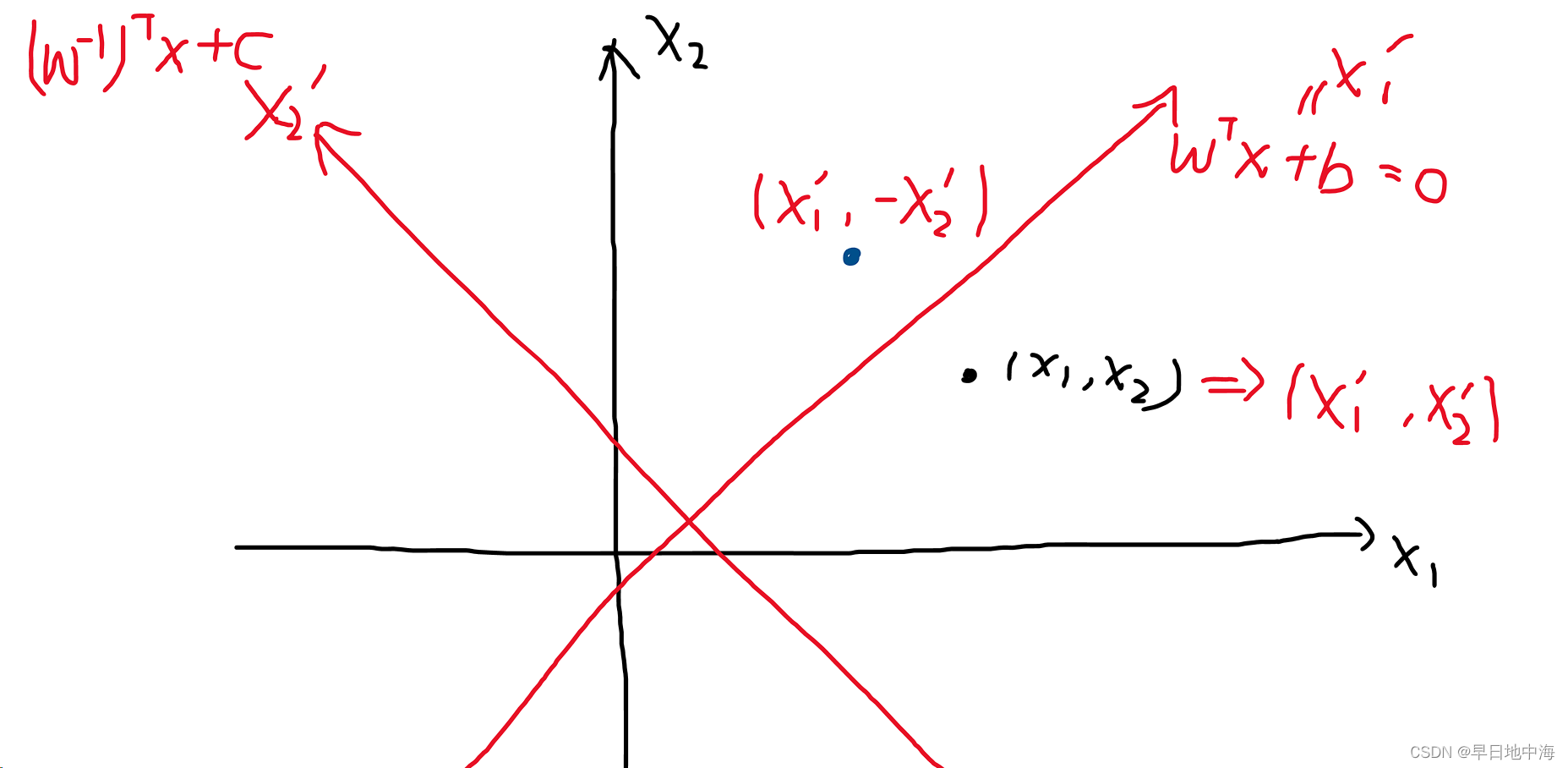
重点来了！这样建立新坐标系的好处就是，可以轻松找到其对称点 $(x_1', -x_2')$ ，因为只需要在第二个变量加个负号就好了。那么好，我们就找这个对称点坐标的具体值，首先第一个变量 $x_1'$ 可以由我们的纵轴决定，在数学上可以说是“不妨”，因此第一个变量我们甚至都可以设为0，只需把纵轴平移到对称点处即可。那么第二个变量 $x_2'$ 应该等于什么？利用初中数学知识：点到直线的距离

$d=\frac{|{\bf wx}+{\bf b}|}{||{\bf w}||}$

于是这里的 $x_2'=d$ ，观察d的表达式，分母是个常数可以不用管，分子不就是仿射变换+非线性激活函数吗？只要把非线性激活函数取一个绝对值整流函数即可，这样，我们在空间中按照任意一个对称轴进行翻折，就可以用一层神经网络来近似。当然，这只是图中一个点，你也可以让这里的x是一条直线，曲线，决策面等等，如果维度上升，我们也可以按照这样的思路进行下去。OK，至此图6.5是不是就好理解了？

以上内容除图与定义皆为原创，转发请注明来源！

早日地中海

关注

1
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
Montufar et al. (2014)论文一些有趣的想法

Montufar et al.(2014)指出一些用深度整流网络表示的函数可能需要浅层网络(一个隐藏层)指数级的隐藏单元才能表示。同时指出分段线性网络（可以通过整流非线性或maxout单元获得）可以表示区域的数量是网络深度的指数级的函数。图6.5解释了带有绝对值整流的网络是如何创建函数的镜像图像的，这些函数在某些隐藏单元的顶部计算，作用于隐藏单元的输入。图来源于花书。读书读到这里的时候，个人感觉花书给出的解释很难读懂，也有可能是自己的能力有限。
复制链接

扫一扫